Uploaded byelisabet Porrini
Redes modulares 2
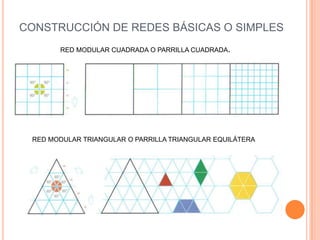
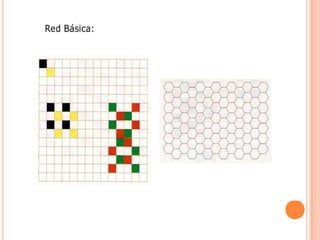
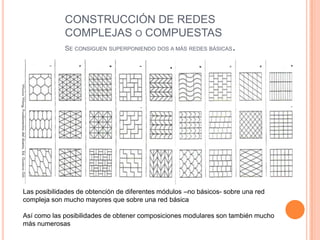
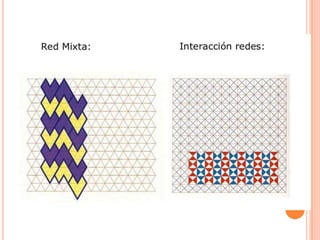
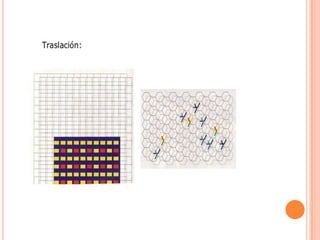
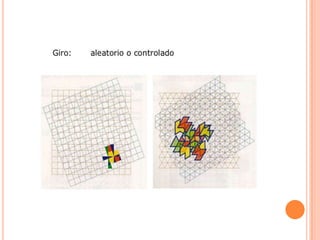
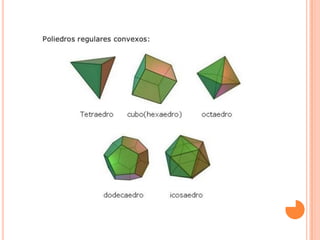
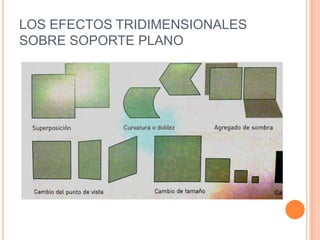
Este documento describe las redes modulares, que son estructuras geométricas formadas por la repetición de figuras llamadas módulos. Explica los tipos básicos de redes modulares creadas a partir de polígonos regulares y cómo construir redes más complejas combinando varias redes básicas. También presenta ejemplos de módulos y redes modulares en la naturaleza, arquitectura y arte, y técnicas para crear efectos tridimensionales en composiciones modulares sobre una superficie plana.
More Related Content
Redes modulares 2
- 1.
- 2. REDES MODULARES DEFINICIONES:REDES Y MÓDULOS. DEFINICIÓN DE MODULO. TIPOS DE REDES MODULARES CONSTRUCCION DE REDES Y MÓDULOS BÁSICOS CONSTRUCCION DE REDES Y MÓDULOS COMPLEJOS LOS MÓDULOS EN NUESTRO ENTORNO COMPOSICIONES MODULARES VARIACIONES MODULARES MOVIMIENTOS DEL MÓDULO. LA CIRCUNFERENCIA EN LA COMPOSICIÓN MODULAR EFECTOS TRIDIMENSIONALES SOBRE SOPORTE PLANO. TRANSFORMACIONES Y ANOMALÍAS
- 3. DEFINICIÓN DE REDESMODULARES Las redes modulares son estructuras, generalmente geométricas, que permiten relacionar figuras iguales o semejantes, llamadas módulos, en una misma superficie. Deben de cubrir la superficie sin dejar huecos intermedios. Las redes que cumplen este requisito son las formadas por triángulos y cuadrados o derivados de estos.
- 4. DEFINICIÓN DE MÓDULO Elmódulo es la figura básica que se repite en las estructuras modulares. La combinación proporcionada de varios módulos sobre una red da lugar a la composición modular. Puede tener diferentes apariencias sobre una red modular. Cuando se combinan varios módulos básicos, da lugar a un “Supermódulo”.
- 5. REDES Y MÓDULOS:TIPOS BASICAS: Se crean a partir de polígonos (triángulos equiláteros, cuadrados, etc.) capaces de generar mayas poligonales cerradas y continuas. MIXTAS: Se crean a partir de la combinación de dos o tres polígonos regulares. En ellas pueden surgir nuevas redes modulares.
- 6. CONSTRUCCIÓN DE REDESBÁSICAS O SIMPLES RED MODULAR CUADRADA O PARRILLA CUADRADA. RED MODULAR TRIANGULAR O PARRILLA TRIANGULAR EQUILÁTERA
- 8. CONSTRUCCIÓN DE REDES COMPLEJASO COMPUESTAS SE CONSIGUEN SUPERPONIENDO DOS A MÁS REDES BÁSICAS. Las posibilidades de obtención de diferentes módulos –no básicos- sobre una red compleja son mucho mayores que sobre una red básica Así como las posibilidades de obtener composiciones modulares son también mucho más numerosas
- 10. MODULOS EN LANATURALEZA
- 11. MÓDULOS EN LAARQUITECTURA
- 17. EJEMPLOS DE ESTRUCTURASMODULARES SIMPLES
- 18. EJEMPLOS DE REDESGEOMÉTRICAS
- 19. MALLAS COMPLEJAS: Si combinamoslas formas geométricas básicas como el cuadrado, triángulos o hexágonos podemos construir nuevas mallas más complejas y más creativas.
- 20. SUB MÓDULO: ESTÁ FORMADOPOR ELEMENTOS IGUALES AL MÓDULO PERO MÁS PEQUEÑOS QUE SE REPITEN UN NÚMERO DETERMINADO DE GENTE.
- 21. DEFORMACIONES Las deformaciones sonvariaciones que aumentan la expresividad de la composición. En el arte argentino Rogelio Pollisello es un representante del arte geométrico y las composiciones en redes.
- 25.
- 27. ESTRUCTURAS MODULARES ENEL ARTE Arte Árabe: Mosaicos
- 33. LA CIRCUNFERENCIA ENLA COMPOSICIÓN MODULAR La circunferencia es una figura que no puede compactar el espacio, al igual que el pentágono, por lo que no hay redes modulares circulares. Pero inscribiéndola en cuadrados se utiliza para diseñar módulos.
- 34. LOS EFECTOS TRIDIMENSIONALES SOBRESOPORTE PLANO En las composiciones modulares se pueden crear sensaciones de espacio tridimensional utilizando diferentes recursos gráficos: Superposición Curvatura o doblez Agregado de sombra Cambio de textura Cambio de punto de vista Cambio de tamaño Cambio de valor o tono
- 35. LOS EFECTOS TRIDIMENSIONALES SOBRESOPORTE PLANO
- 36. LOS EFECTOS TRIDIMENSIONALESSOBRE SOPORTE PLANO
- 37. TRANSFORMACIONES Y ANOMALÍAS TRANSFORMACIONES ANOMALÍAS
- 38. UNA ACTIVIDAD APARENTEMENTECOMPLICADA, PERO EN REALIDAD MUY SENCILLA, ES LA CREACIÓN DE REDES MODULARES. LO PRIMERO ES DISEÑAR UN MÓDULO O UNIDAD BÁSICA, LA QUE POSTERIORMENTE REPETIREMOS UNA Y OTRA VEZ. EL MÓDULO SE PUEDE CREAR A PARTIR DE CUALQUIER FORMA, AUNQUE LOS POLÍGONOS REGULARES COMO EL TRIÁNGULO EQUILÁTERO, EL CUADRADO Y EL HEXÁGONO, SON LAS FIGURAS GEOMÉTRICAS QUE PERMITEN APROVECHAR EL ESPACIO SIN DEJAR NINGÚN HUECO. DESPUÉS, REALIZAMOS UNA DIVISIÓN INTERNA DE LA FORMA ELEGIDA, EN ESTE CASO UN CUADRADO Ya tenemos nuestro módulo, ahora tenemos que decidir de qué manera o con qué criterio vamos a repetirlo. Estos son solo ejemplo. Ahora te propongo hacer tu modulo y repetirlo, combinarlo y crear redes modulares.