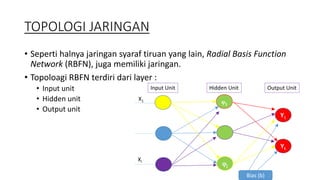
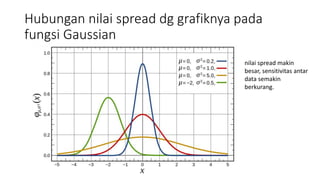
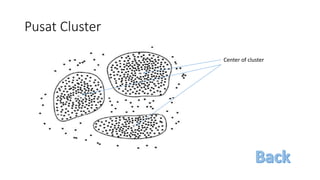
Dokumen ini membahas tentang Radial Basis Function Network (RBFN) sebagai sistem pakar dalam topologi jaringan, yang terdiri dari unit input, hidden, dan output. RBFN digunakan untuk pengklasifikasian pola dan pemodelan deret waktu dengan fungsi aktivasi berbasis radial, seperti fungsi Gaussian, dan memiliki algoritma pelatihan yang mencakup tahap clustering data dan pembaharuan bobot. Selain itu, dokumen tersebut juga menjelaskan variasi fungsi aktivasi dan metode untuk menentukan pusat cluster dalam tahap clustering.

2. RADIAL BASIS FUNCTION
SISTEM PAKAR

3. TOPOLOGI JARINGAN
• Seperti halnya jaringan syaraf tiruan yang lain, Radial Basis Function
Network (RBFN), juga memiliki jaringan.
• Topoloagi RBFN terdiri dari layer :
• Input unit
• Hidden unit
• Output unit
1
j
Y1
Yk
Bias (b)
X1
Xi
Input Unit Hidden Unit Output Unit

4. Sifat Khusus RBFN
• Pemrosesan dari Input ke hidden bersifat non-linier
• Pemrosesan dari hidden ke output bersifat linier
• Pada hidden layer digunakan fungsi aktivasi yang berbasis radial,
misalnya fungsi Gaussian
• Pada output unit , sinyal dijumlahkan seperti biasa
• Sifat jaringannya adalah feed forward

5. Fungsi Gaussian
• 휑 푟 = 푒푥푝 −
푟2
2휎2 untuk 휎 > 0
• Dimana ∶ 휎  nilai spread
• 휎 =
푀푎푥.퐷푖푠푡푎푛푐푒 푏푒푡푤푒푒푛 푎푛푦 2 푐푒푛푡푒푟푠
푛푢푚푏푒푟 표푓 푐푒푛푡푒푟푠
=
푑푚푎푥
푚1
• Nilai spread menentukan bagaimana data tersebar. Jika nilai
spread makin besar, sensitivitas antar data semakin
berkurang.
• Centers adalah pusat cluster data

6. Hubungan nilai spread dg grafiknya pada
fungsi Gaussian
nilai spread makin
besar, sensitivitas antar
data semakin
berkurang.

7. Fungsi Aktivasi selain Fungsi Gaussian
• Multi-Quadric Functions
∅ 푟 = (푟2 + 휎2)1/2 parameter  >0
• Generalized Multi-Quadric Functions
∅ 푟 = 푟2 + 휎2 훽 parameter >0, 1>>0
• Inverse Multi-Quadric Functions
∅ 푟 = 푟2 + 휎2 −1/2 푝푎푟푎푚푒푡푒푟 휎 > 0
• Generalized Inverse Multi-Quadric Functions
∅ 푟 = 푟2 + 휎2 −훼 푃푎푟푎푚푒푡푒푟 휎 > 0, 1 > 훼 > 0
• Thin Plate Spline Function
∅ 푟 = 푟2 ln 푟
• Cubic Function
∅ 푟 = 푟3
• Linear Function
∅ 푟 = 푟

8. RBFN
• Biasa digunakan untuk menyelesaikan 2 jenis permasalahan, yaitu :
• Pattern Classification
• Time series modelling
• Untuk Pattern Classification menggunakan fungsi aktivasi Gaussian
• Time Series Modelling menggunakan fungsi aktivasi thin-plate spline

9. Algoritma Pelatihan Jaringan
• Berguna atau tidaknya suatu JST ditentukan dari hasil pelatihan
(bobot neuron-nya)
• RBFN mempunyai algoritma pelatihan yang agak unik, karena terdiri
dari cara Supervised dan unsupervised sekaligus.
• Pelatihan RBFN terdiri dari 2 tahap, yaitu :
1. Tahap Clustering Data
2. Pembaharuan Bobot

10. Tahap 1 : Clustering Data
• Data di cluster / dikelompokkan berdasarkan kedekatan tertentu
(misalnya kedekatan 2 warna pixel, kedekatan jarak 2 titik, dll)
• Penentuan cluster akan memunculkan center / pusat cluster dari
kelompok data
• Jumlah cluster menentukan jumlah hidden unit yg dipakai
• Cara menentukan center ada 2, yaitu :
1. Menentukan center secara acak dari sekelompok data (paling mudah)
2. Menggunakan algoritma clustering. Algoritma yang paling mudah adalah K-Means.
Dengan Algoritma ini, JST mampu mencari sendiri center yg terbaik.
• Melihat cara tersebut, maka jelas tahap 1 ini adalah unsupervised

11. Tahap 2 : Pembaharuan Bobot
• JST menyimpan pengetahuannya dalam bobot neuron-neuronnya.
• Bobot diperbaharui melalui serangkaian perhitungan.
• Dibutuhkan data training dan target (supervised)

12. Langkah2 Tahap 2
• Meneruskan sinyal input ke hidden & menghitung nilai aktivasi pada
tiap hidden layer
휑 푋푚 − 푡푗 = 푒
푋푚−푡푗
휎2
Dimana :
• M = 1,2,3….sesuai dg jumlah training pattern
• J = 1,2,3…. Sesuai dengan jumlah hidden unit
• X  vector input
• T  vector data yg dianggap sebagai center

13. Langkah2 Tahap 2
• Menyusun matriks Gaussian dari hasil perhitungan langkah 1
• 퐺 =
휑11 휑12 … .
휑21 휑22 … .
… . … . … .
휑1푐
휑2푐
… .
휑푚1 휑푚2 … . 휑푚푐
• Dimana : m  vector input ke-m
c  hidden unit ke-c

14. Langkah2 Tahap 2
• Menghitung bobot baru (w) dengan mengalikan pseudoinvers dari
matrik G, dengan vector target (d) dari data training.
Rumus : W = G+d
= (GTG)-1 GTd
• Menghitung nilai output JST :
푦 푥 = 푡=1 푤퐺 푥 − 푡푡 + 푏
Dimana b  nilai bobot bias
G(x) pada rumus ini artinya sama dengan (x)

15. Pusat Cluster
Center of cluster