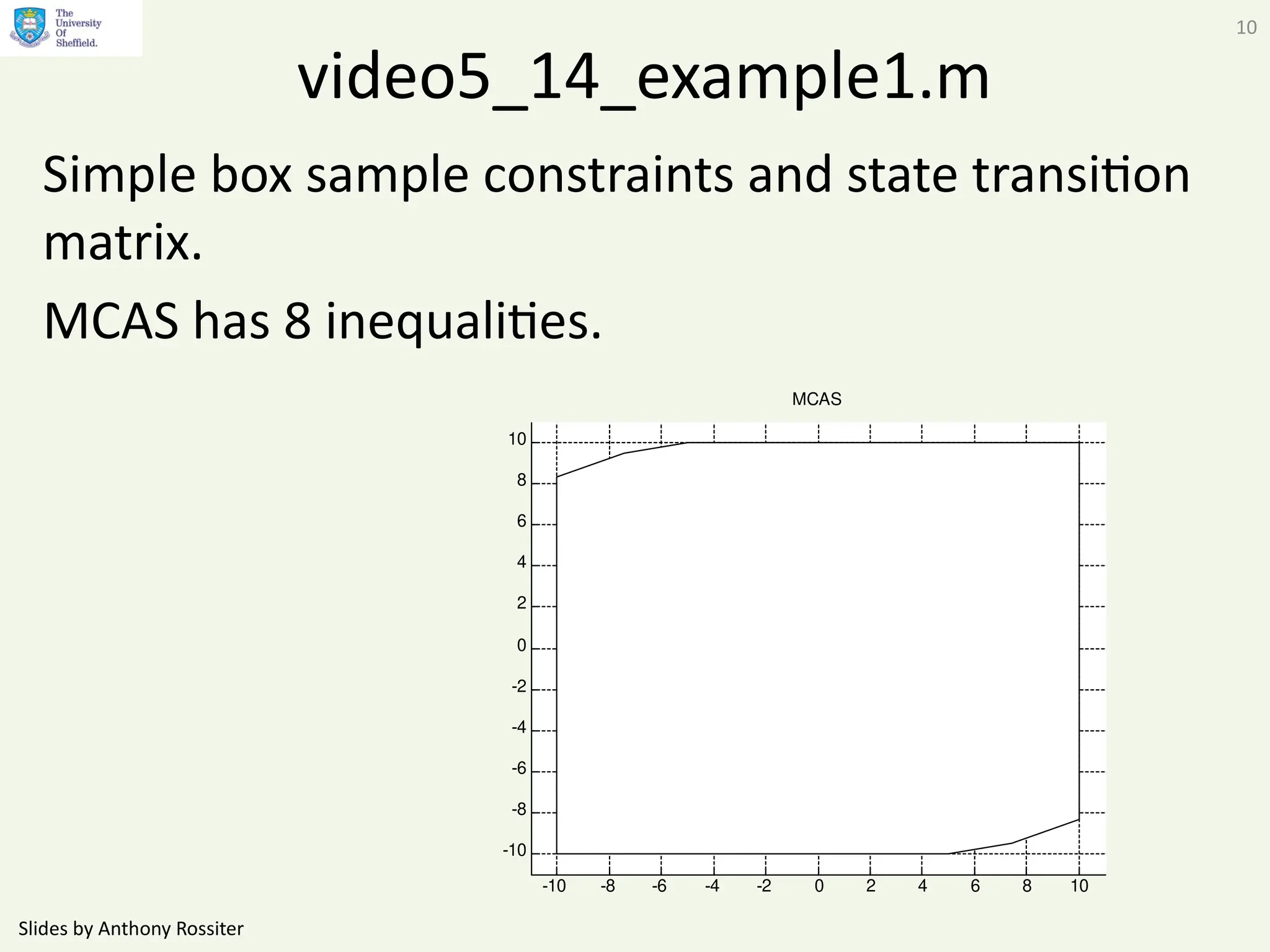
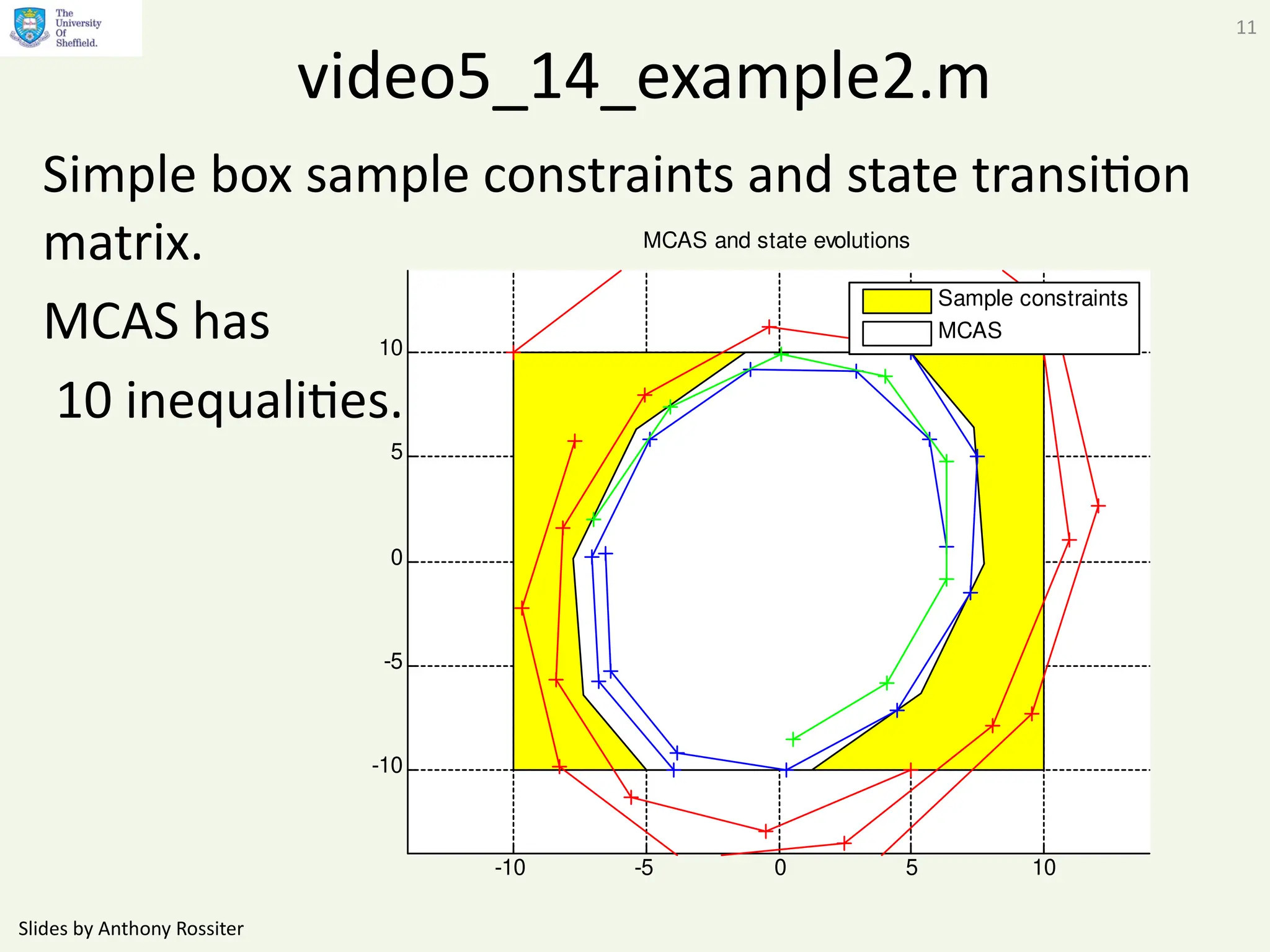
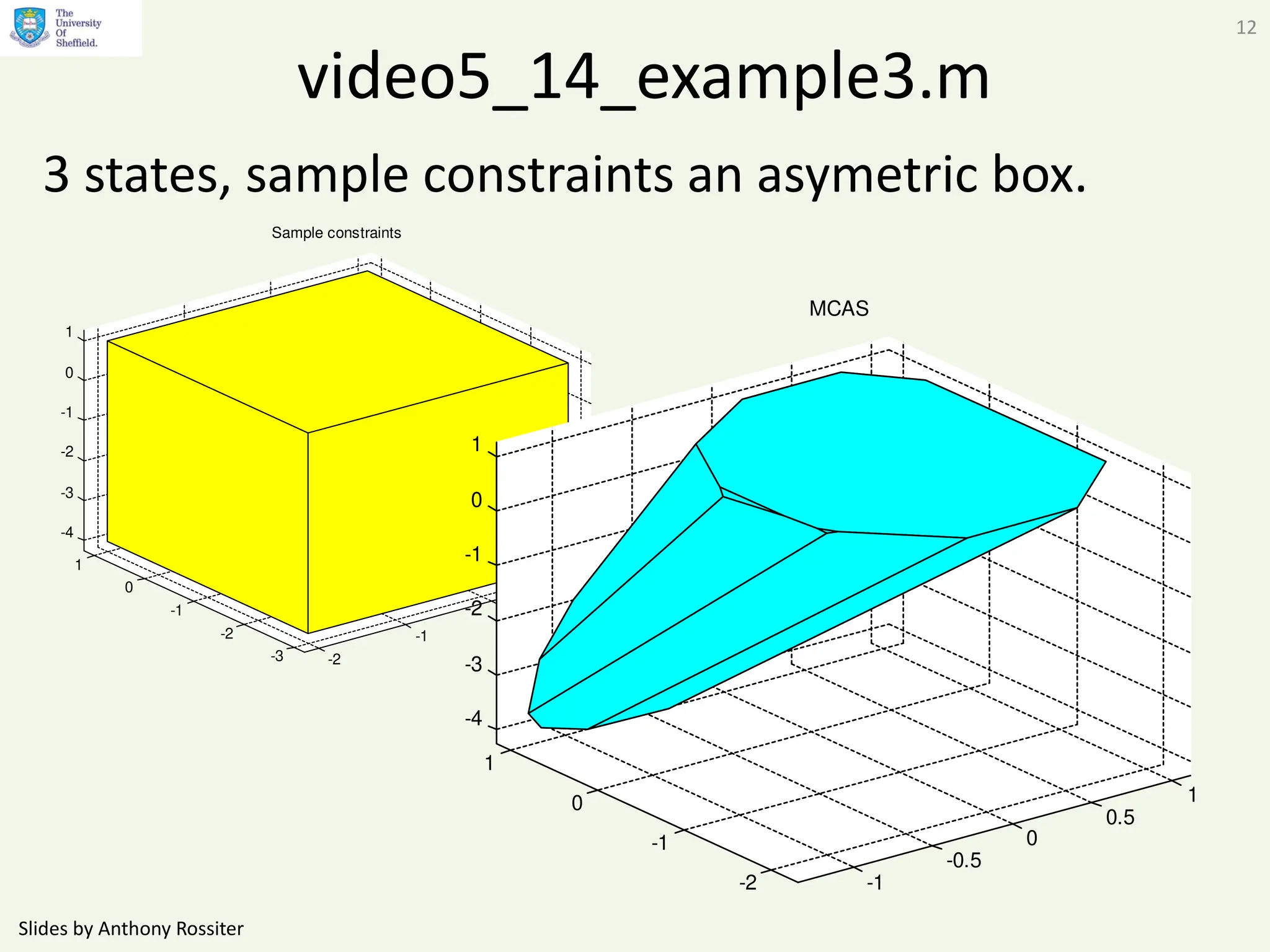
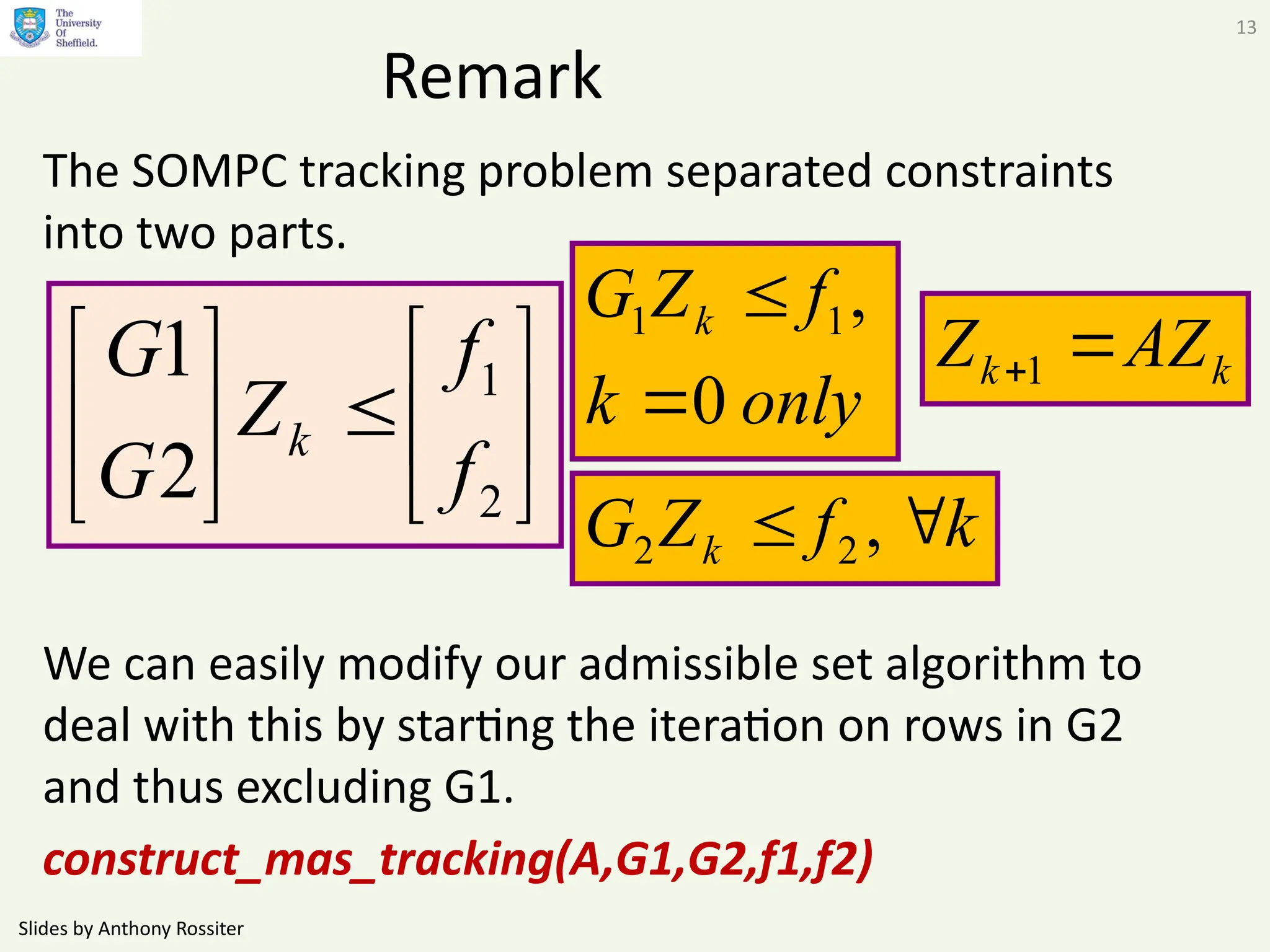
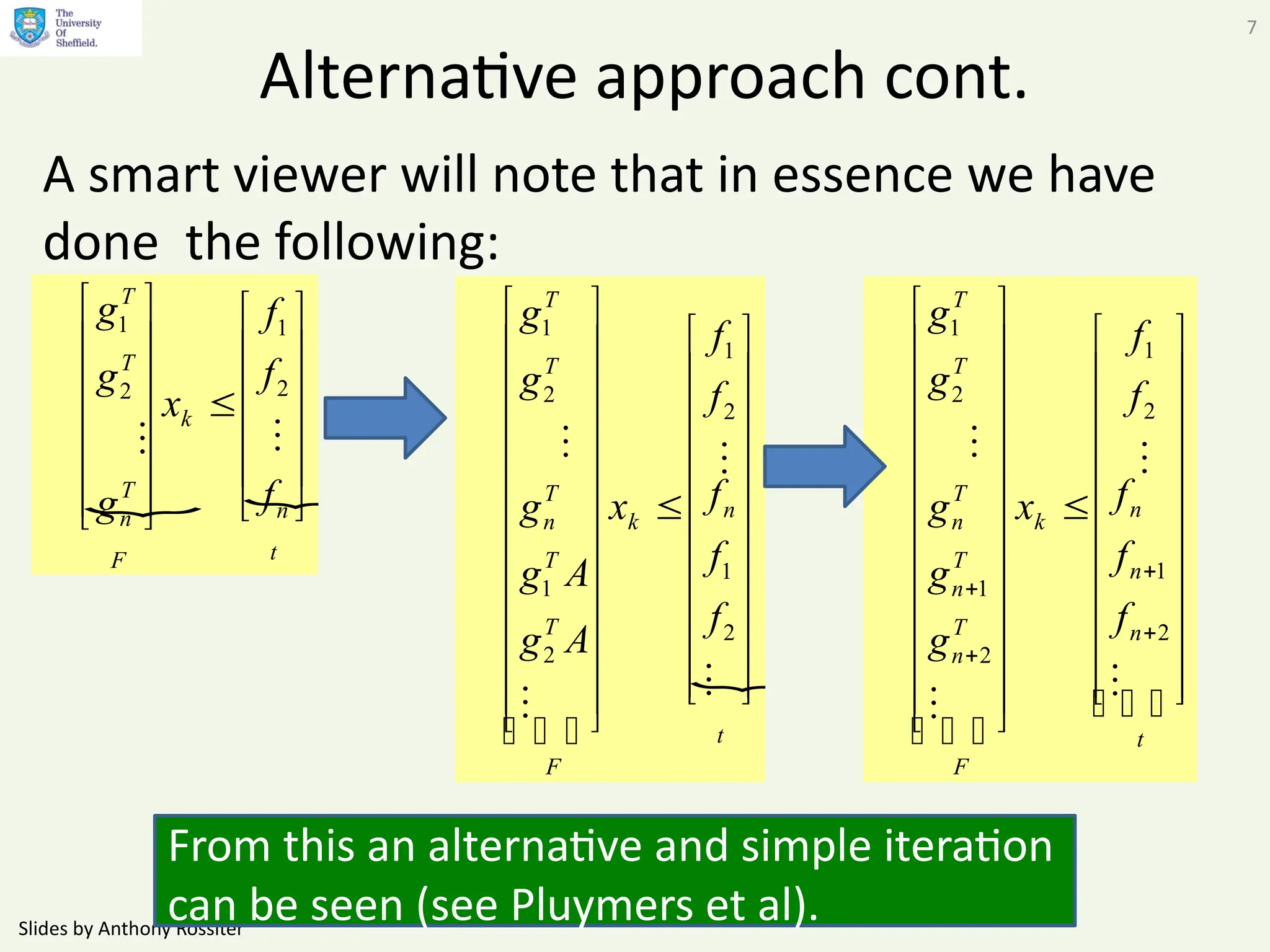
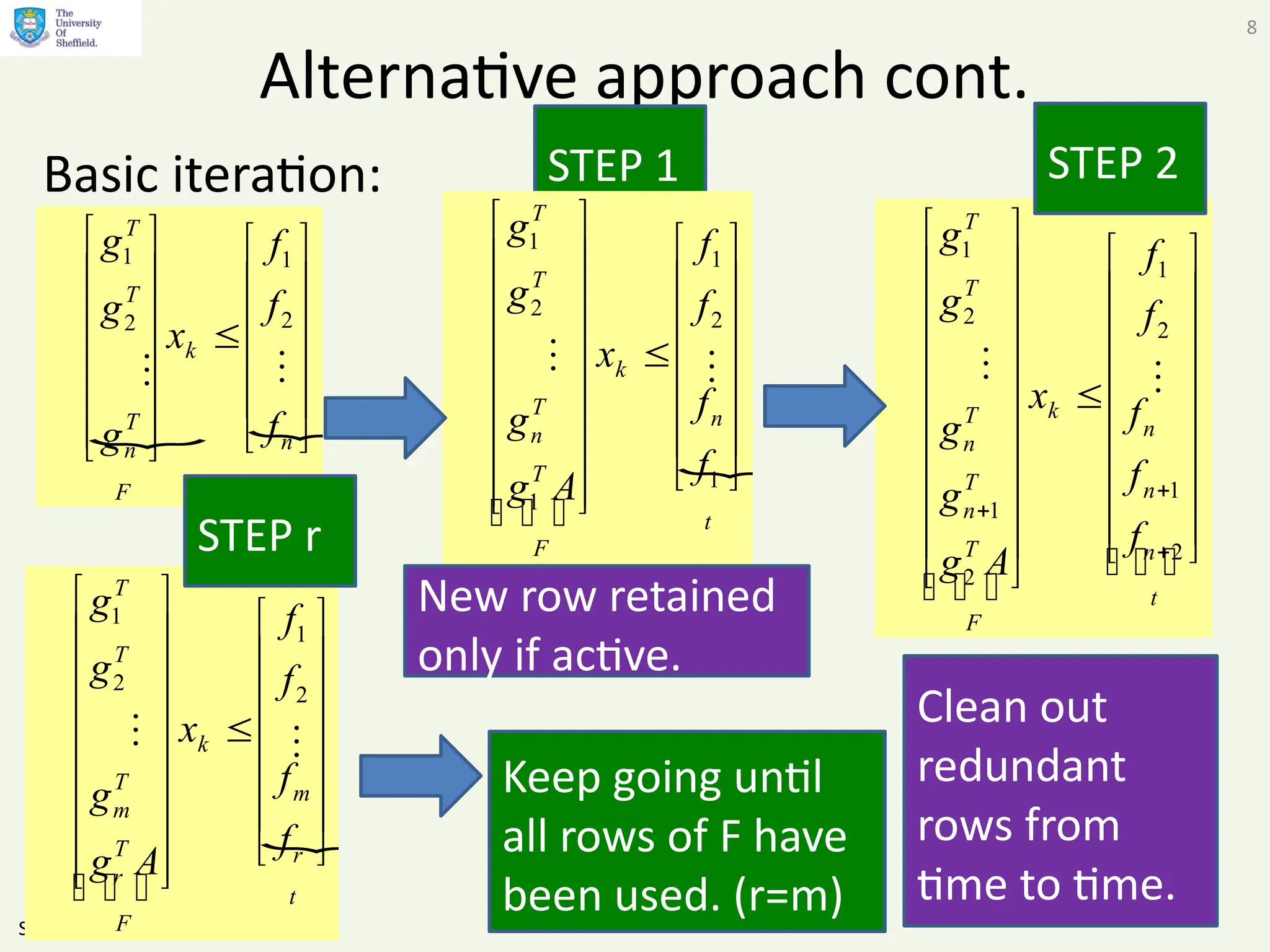
This document presents alternative admissible set algorithms for predictive control with constraints, emphasizing the importance of efficient constraint management over possibly infinite horizons. It discusses methods for eliminating redundant constraints and iterative approaches to ensure convergence while maintaining constraints over varying dimensions. The video also explores applications to the SOMPC algorithm and examines the typical number of inequalities required in different scenarios.






![Slides by Anthony Rossiter
9
MATLAB code
The relevant file is in the constraints examples
folder. [Modified from an original by Bert Pluymers]
Called construct_mas.m
e.g. construct_mas(A,G,f)
LACK of convergence is usually linked to the user
entering a state transition matrix ‘A’ which does not
have stable eigenvalues.
Also, the code does not check for ‘feasibility’](https://image.slidesharecdn.com/predictivecontrolwithconstraints5-14-alternativeadmissiblesetalgorithms-241108141931-15e8a312/75/predictive-control-with-constraints-5-14-alternative-admissible-set-algorithms-pptx-9-2048.jpg)