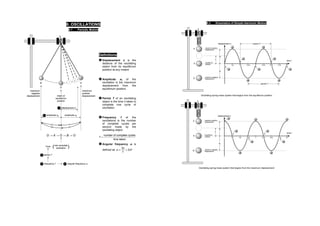
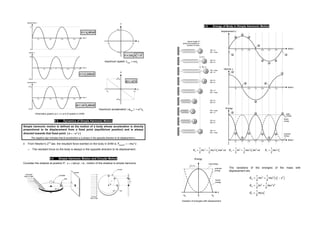
This document discusses oscillations and simple harmonic motion. It defines key terms like period, frequency, displacement, and amplitude. It describes the kinematics and dynamics of simple harmonic motion for a spring-mass system. Specifically, it states that the acceleration of an object in SHM is directly proportional to and opposite of its displacement from equilibrium. It also discusses the energies involved, including kinetic, potential, and total energy, and how they vary with displacement. Damping is described as causing the amplitude and total energy to decrease exponentially over time. The interaction of an oscillating system with an external periodic driving force is also summarized.

1. 8. OSCILLATIONS
8.1 Periodic Motion
Definitions
➊ Displacement x is the
distance of the oscillating
object from its equilibrium
position at any instant
➋ Amplitude x0 of the
oscillation is the maximum
displacement from the
equilibrium position.
➌ Period T of an oscillating
object is the time it takes to
complete one cycle of
oscillation.
➍ Frequency f of the
oscillations is the number
of complete cycles per
second made by the
oscillating object.
f =
number of complete cycles
time taken
➎ Angular frequency ω is
defined as ω =
2π
T
= 2πf
8.2 Kinematics of Simple Harmonic Motion
Oscillating spring-mass system that begins from the equilibrium position
Oscillating spring-mass system that begins from the maximum displacement

2. Kinematics graphs (x-t, v-t, a-t) of system in SHM
maximum speed vmax
= ωx0
maximum acceleration | amax
| = ω2
x0
8.3 Dynamics of Simple Harmonic Motion
Simple harmonic motion is defined as the motion of a body whose acceleration is directly
proportional to its displacement from a fixed point (equilibrium position) and is always
directed towards that fixed point. ( a = −ω2
x )
The negative sign indicates that its acceleration a is always in the opposite direction to its displacement x.
• From Newton’s 2nd
law, the resultant force exerted on the body in SHM is Fresultant
= −mω2
x
o The resultant force on the body is always in the opposite direction to its displacement.
8.4 Simple Harmonic Motion and Circular Motion
Consider the shadow at position P, x = r sinωt , i.e., motion of the shadow is simple harmonic
x = x0
sinωt
v = v0
cosωt
a = −ω2
x0
sinωt
v = ±ω x0
2
− x2
a = −ω2
x
8.5 Energy of Body in Simple Harmonic Motion
EK
=
1
2
mv2
=
1
2
mω 2
x0
2
cos2
ωt EP
=
1
2
kx2
=
1
2
mω 2
x0
2
sin2
ωt ET
=
1
2
mω 2
x0
2
Variation of energies with displacement
The variations of the energies of the mass with
displacement are
EK
=
1
2
mv2
=
1
2
mω2
x0
2
− x2
( )
EP
=
1
2
kx2
=
1
2
mω2
x2
ET
=
1
2
mωx0
2

3. 8.6 Damping
Energy is lost continuously due to resistive forces. The total energy and the amplitude decrease.
Exponential decrease of amplitude with light damping Displacement with time for different degree of damping
• The job of a car suspension is to
o maximise the contact between the tyres and the road surface (as a result leading to better
handling in terms of steering stability),
o ensure the comfort of the passengers.
• Roads have subtle imperfections that can interact with the wheels of a car.
o The wheel experiences a vertical force as it passes over a bump.
o Without an intervening structure, the entire car moves in the same direction and the wheels
lose contact with the road, causing problem in handling.
o Under gravity, the wheels will slam back into the road surface.
• To minimise such effects, a system that will absorb the energy of the vertically accelerated
wheel will allow the car frame to be undisturbed.
• A car suspension system includes springs and shock absorbers.
o When the wheel hits a bump, the vertical force on the wheel compresses the spring,
keeping the wheel to remain in contact with the road.
o When the spring expands, the viscous oil in the shock absorber slows its motion, enabling
the spring to smoothly return to its equilibrium length without oscillating.
o A good suspension system is one in which the damping is slightly under critical damping as
this results in a comfortable ride for the passengers along a bumpy road.
8.7 Interaction of oscillating system with external periodic force
• The periodic external force provides a means of supplying energy to the system.
• The system will response to driving force as follow:
o Initially its oscillation is complicated that includes components of its natural frequency and
the driving force frequency.
o Given sufficient time, steady state is reached and the system oscillates in the same
frequency as the driving force.
When the frequency of the external periodic force is equal to the natural frequency of the
oscillating system, the amplitude of the oscillation is large.
System response to periodic driving force
• As the degree of damping increases,
o amplitude of oscillation at all
frequencies is reduced
o frequency at maximum amplitude
shifts gradually towards lower
frequencies
o peak becomes flatter.