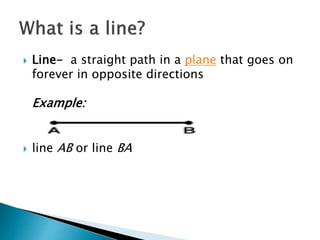
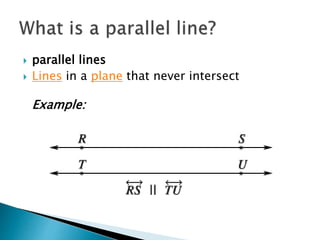
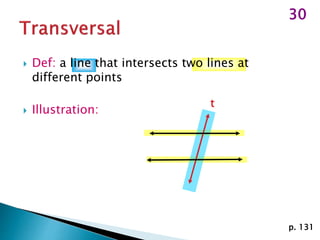
This document defines and provides examples of geometric terms including: lines, line segments, points, parallel lines, complementary angles, supplementary angles, transversal lines, and vertical angles. Complementary angles sum to 90 degrees, while supplementary angles sum to 180 degrees. Vertical angles are opposite and equal.

2.  Line- a straight path in a plane that goes on
forever in opposite directions
Example:
 line AB or line BA

3.  point
 An exact location in space, usually
represented by a dot
Example:
point A

4.  line segment
 A part of a line that includes two points,
called endpoints, and all of the points
between them
Example:
 line segment AB or line segment BA

5.  parallel lines
 Lines in a plane that never intersect
Example:

7.  Two angles are complementary
if the sum of their angles equals
90*.
 If one angle is known, its
complementary angle can be
found by subtracting the
measure of its angle from 90*.

8.  What is the complementary angle of 43*?
◦ SOLUTION: 90* - 43* = 47*
◦ So, 43* and 47* are complementary angles
 Angle A measures 25* and Angle B measures 65*.
Angle A and Angle B are complementary angles
because together they create a 90* angle.
◦ JUSTIFICATION: 25* + 65* = 90*

9.  Two angles are supplementary if
the sum of their angles equals
180*.
 If one angle is known, its
supplementary angle can be
found by subtracting the
measure of its angle from 180*.

10.  What is the supplementary angle of 143*?
◦ SOLUTION: 180* - 143* = 37*
 Angle A measures 120* and Angle B measures 60*.
Angle A and Angle B are complementary angles
because together they create a 180* angle.
◦ JUSTIFICATION: 120* + 60* = 180*

11.  Def: a line that intersects two lines at
different points
 Illustration:
t
p. 131
30

12.  Two angles that are opposite angles.
1 2
3 4
5 6
7 8
t
1   4
2   3
5   8
6   7