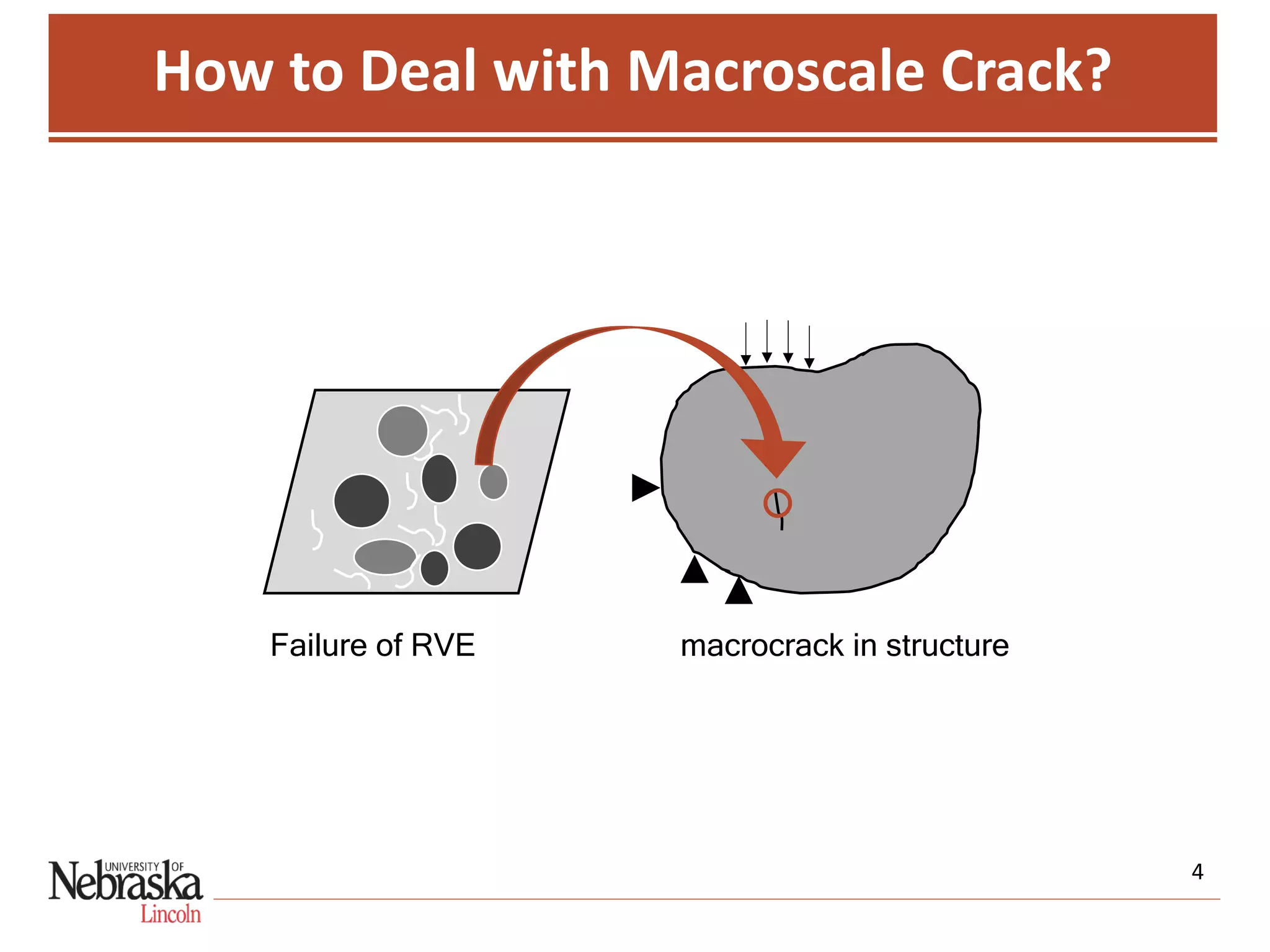
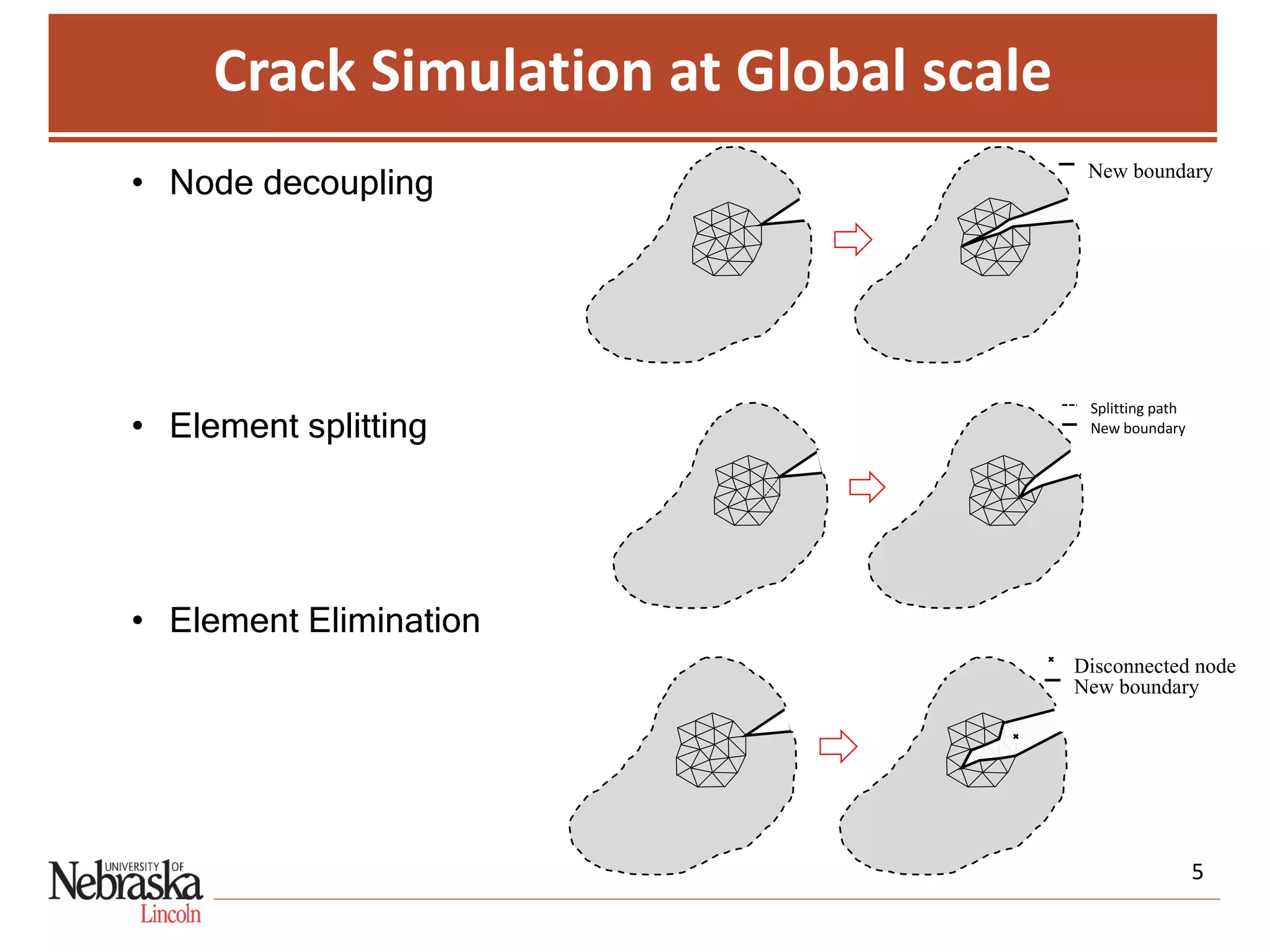
This document discusses a multiscale simulation approach for modeling fracture in quasi-brittle materials. The approach divides the system into global and local scales, with each scale solved separately and linked through homogenization. At the global scale, cracks are simulated using node decoupling, element splitting, or element elimination. The global-scale solution is applied to the local-scale, which is then homogenized and used to update the global-scale properties. This allows using larger-scale testing results to indirectly characterize smaller-scale material properties and investigate the effect of heterogeneity on performance. The approach is applied to model fracture in cementitious paste.

1. 1
Multiscale simulation of fracture in
quasi-brittle mixtures
Keyvan Zare Rami, 2018

2. 2
Multiscale Fracture Simulation
Void growth model
Cell Model
• The cell is the smallest material unit that has sufficient information
about crack growth in the material
Andersson, H., Journal of the Mechanics and Physics of Solids (1977)
Broberg, K. B., Computational Mechanics (1997)

3. 3
Two-way Linked Multiscale Simulation
• System is divided into two length-scale: Global scale and Local scale
• Each length-scales will be solved separately
• The length-scales are linked through homogenization principles
Apply stress or strain to RVE
Solve RVE under boundary condition
Homogenize properties
Global scale
Local scale

4. 4
How to Deal with Macroscale Crack?
Failure of RVE macrocrack in structure

5. 5
• Node decoupling
• Element splitting
• Element Elimination
Crack Simulation at Global scale
New boundary
New boundary
Splitting path
New boundary
Disconnected node

6. 6
Implementation of Crack Simulation at Global
Scale
Solve global-scale
BVP
Apply global-scale
displacement solution to
local-scale BVP
Solve local-scale BVP
End
Next time step?
Homogenize local-
scale solution
Update global-scale
properties
Yes
No
Form global-scale
initial BVP
Remove or split
global-scale failed
element
Renumbering the
FE mesh
Reconstruct BC
Is RVE failed?
NoYes
RepeatedoverglobalFEslinkedtoRVE

7. 7
Application on Cementitious Paste

8. 8
Conclusion
• This approach provides a capability of using larger length-scale
testing result, which are usually more feasible to obtain, to
characterize smaller length-scale properties indirectly by linking
between different length-scales.
• It provides opportunities to investigate the effect of smaller length-
scale heterogeneity on larger length-scale performance of
materials.

9. 9
Contact
www.linkedin.com/in/keyvan-zare
keyvan.zare@gmail.com