The document analyzes the aerodynamic behavior of super slender monolithic towers, emphasizing their vulnerability to wind due to high slenderness ratios, ranging from 15:1 to 24:1. It investigates the effects of vortex shedding and the importance of wind-induced vibrations, including critical wind speeds and testing methodologies like aeroelastic and pressure tests. The results highlight the relevance of both first and second order modes of vibration in the design of these structures, particularly under turbulent wind conditions.





![6
D. Anagnostopulos The Aerodynamic Behaviour of Super Slender Monolithic Towers
Ideal structure and its location
Structural Properties
Full Scale Properties
B [m] 20.00
B [m] 20.00
r [m] 2.00
Floor Area [m2] 396.57
Height of building [m] 400.00
Volume [m3] 158626.55
Density [Kg/m3] 250.00
Mass x unit height[Kg/m] 99141.59
Frequency Frequency
1st order mode 2nd order mode
(Hz) (Hz)
0.08 0.24
𝑛2𝑜𝑟𝑑𝑒𝑟
𝑛1𝑜𝑟𝑑𝑒𝑟
≈ 3.0
Dynamic Properties
Slenderness ratio
20:1](https://image.slidesharecdn.com/mscthesisanagnostopulos-170313203219/85/Msc-thesis-Anagnostopulos-Danai-Iris-6-320.jpg)
![9
D. Anagnostopulos The Aerodynamic Behaviour of Super Slender Monolithic Towers
Design of the aeroelastic model
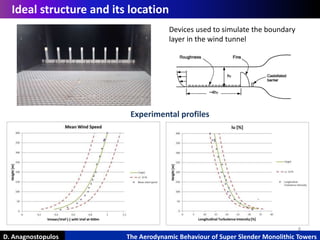
Scaling parameters
Froude Number
Cauchy Number
Reynolds Number
Density parameter
Damping Ratio
Quantity Scaling Factor
Length 𝑓𝐿=𝐿 𝑚/𝐿 𝑝=1:400
Air density 𝑓∆=1:1
Mass 𝑓∆x𝑓𝐿
3
=1:4003
Structural Damping Ratio f=1:1
Fundamental Frequencies 𝑓𝑇= 𝑓𝑚/𝑓𝑝
Wind Velocity 𝑓𝑉= 𝑓𝑇x𝑓𝐿
Time 𝑓𝑡=1/𝑓𝑇
Force 𝑓𝐹= 𝑓𝛥x𝑓𝑉
2
x𝑓𝐿
2
Bending Moment 𝑓 𝑀= 𝑓𝛥x𝑓𝑉
2
x𝑓𝐿
3
Acceleration 𝑓𝐴=𝑓𝐿/𝑓𝑡
2
Full Scale Properties Model Scale Properties
B [m] 20.0 B [m] 0.05
B [m] 20.0 B [m] 0.05
r [m] 2.0 r [m] 0.01
Floor Area [m2] 396.6 Floor Area [m2] 0.002
Height of building [m] 400.0 Height of building [m] 1.00
Volume [m3] 158626.5 Volume [m3] 0.002
Density [Kg/m3] 250.0 Density [Kg/m3] 250.0
Mass x unit height[Kg/m] 99141.6 Mass x unit height[Kg/m] 0.6
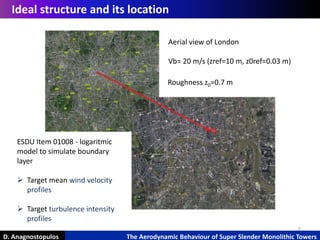
Similitudine requirements
Approach used only for very important
structures
Most reliable approach to predict
building’s dynamic response to wind
action
Simulates: mass, stiffness, damping of
actual structure
Flexes in response to the wind as the
real structure](https://image.slidesharecdn.com/mscthesisanagnostopulos-170313203219/85/Msc-thesis-Anagnostopulos-Danai-Iris-9-320.jpg)

![12
D. Anagnostopulos The Aerodynamic Behaviour of Super Slender Monolithic Towers
Design of the aeroelastic model
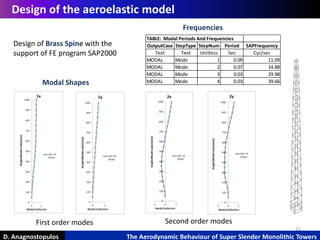
Construction
Outer Shell
Complete aeroelastic model
Density SLS thikness Vtot shell Mass shell
[kg/m3] [m] [m3] [kg]
900 0.002 0.0004 0.330
Derived by selective laser sintering
Formed by 10 vertical segments
1mm gap in between the segments
Instrumentation
Accelerometers 2 at the top
2 at the antinode](https://image.slidesharecdn.com/mscthesisanagnostopulos-170313203219/85/Msc-thesis-Anagnostopulos-Danai-Iris-12-320.jpg)
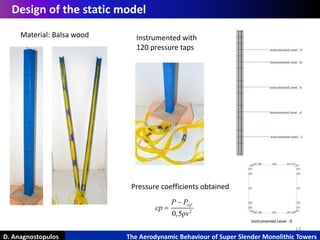
![14
D. Anagnostopulos The Aerodynamic Behaviour of Super Slender Monolithic Towers
Setup of aeroelastic tests
Calibration
Mode shapes
check
Frequency check
SAP Model WT Model
Mode Direction Frequency [Hz] Frequency [Hz]
1 X-Along 11.1 12.4
1 Y-Cross 14.9 13.8
2 X-Along 30.0 28.7
2 Y-Cross 39.7 44.0
𝑛2𝑜𝑟𝑑𝑒𝑟𝑊𝑇
𝑛1𝑜𝑟𝑑𝑒𝑟𝑊𝑇
= 3.3](https://image.slidesharecdn.com/mscthesisanagnostopulos-170313203219/85/Msc-thesis-Anagnostopulos-Danai-Iris-14-320.jpg)





![D. Anagnostopulos The Aerodynamic Behaviour of Super Slender Monolithic Towers
Pressure data analysis
The crosswind correlation
becomes very weak at a distance
equal to 120 m (i.e. 6 times the
cross-section side), similarly to
classic formulation in the
technical literature (e.g., the
harmonic method in EC1/CNR)
z Correl coeff Correl coeff
[m] cross along
340 1.00 1.00
300 0.64 0.73
220 0.12 0.46
140 0.01 0.33
,
,
( )i j
i j
i j
Cpp
,
1
1
( ) ( )( )
n
i j hi hi hj hj
h
Cpp cp mcp cp mcp
n
](https://image.slidesharecdn.com/mscthesisanagnostopulos-170313203219/85/Msc-thesis-Anagnostopulos-Danai-Iris-20-320.jpg)
![21
D. Anagnostopulos The Aerodynamic Behaviour of Super Slender Monolithic Towers
Structural response analysis
𝑆𝑐𝑖 =
4𝜋𝑚 𝑒,𝑖ξ 𝑖
𝜌𝐵2
m ξ ρ B Sc,i
[Kg/m] [-] [Kg/m3] m [-]
mode 1y 99141 0.0058 1.25 20 14
mode 2y 99141 0.0049 1.25 20 12
Scruton Number
CNR
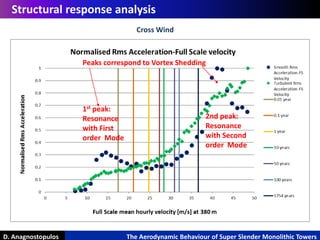
Low structural frequencies lead to resonance for both first and second order mode of vibration
Critical velocities migrate along the axis of the structure:
First order mode excited by vortex shedding for low wind speeds, at the top
Second order mode excited by higher velocities and has to be analysed for more critical
positions with regards to vortex shedding
Low values of Scruton Number show that the structure
is sensible to vibrations induced by vortex shedding](https://image.slidesharecdn.com/mscthesisanagnostopulos-170313203219/85/Msc-thesis-Anagnostopulos-Danai-Iris-21-320.jpg)