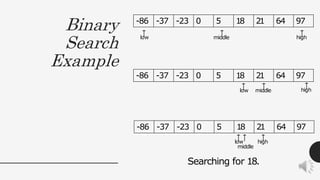
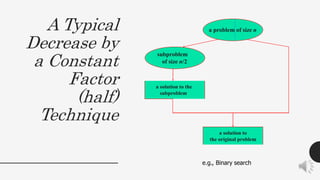
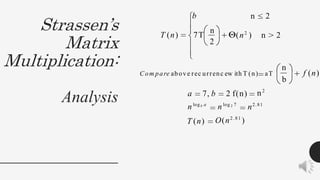The document discusses several algorithm design strategies including brute force, divide and conquer, and decrease and conquer. It provides examples of each strategy, including string matching and linear search as brute force algorithms. Merge sort and Strassen's matrix multiplication are presented as divide and conquer algorithms, with analysis of their time complexities. Binary search is analyzed as a decrease and conquer algorithm with logarithmic time complexity.

1. MODULE 2
DESIGN ANALYSIS AND ALGORITHMS
CREATED AND NARRATED BY – ARYANVARSHNEYA(18BCE10064)

2. INDEX • Brute Force Approach
String Matching
• Analysis of Linear Search
• Divide and Conquer
Merge Sort
• Strassen’s Matrix Multiplication
• Analysis of Binary Search
• Decrease and Conquer

3. Brute Force
Approach
• Brute force - the simplest of the design strategies
• Is a straightforward approach to solving a problem,
usually directly based on the problem’s statement and
definitions of the concepts involved.
• Just do it - the brute-force strategy is easiest to apply.
• Results in an algorithm that can be improved with a
modest amount of time.
• Brute force is important due to its wide applicability
and simplicity.
• Weakness is subpar efficiency of most brute-force
algorithms.
• Important examples:
• – Selection sort, String matching,Convex-hull
problem, and Exhaustive search

4. BFA:
String
Matching
• Align the pattern against the first m characters of the
text and start matching the corresponding pairs of
characters from left to right until all m pairs match.
But, if a mismatching pair is found,
• then the pattern is shift one position to the right and
character comparisons are resumed.
• The goal is to find i - the index of the leftmost
character of the first matching substring in the text
• – such that ti = p0,….ti+j = pj, …..ti+m-1 = pm-1

5. BFA:
String
Matching
(Cont…)
• Algorithm BruteForceStringMatching (T[0..n - 1],
P[0..m - 1])
• //Implements string matching
• //Input:An arrayT[0..n - 1] of n characters representing
a text
• // an array P[0..m - 1] of m characters representing a
pattern
• //Output:The position of the first character in the text
that starts the first
• // matching substring if the search is successful and -1
otherwise.
• for i ← 0 to n - m do j ← 0
• while j < m and P[j] =T[i + j] do j ← j + 1
• if j = m return i return -1

6. .
BFA:
String
Matching
(Cont…)

7. Linear
Search
Example
element
-23 97 18 21 5 -86 64 0 -37
-23 97 18 21 5 -86 64 0 -37
-23 97 18 21 5 -86 64 0 -37
-23 97 18 21 5 -86 64 0 -37
-23 97 18 21 5 -86 64 0 -37
element
element
element
element
element
Searching for -86.

8. Analysis
of
Linear
Search
How long will our search take?
• In the best case, the target value is in the first element of
the array.
• So the search takes some tiny, and constant, amount of
time.
• In the worst case, the target value is in the last element of
the array.
• So the search takes an amount of time proportional to the
length of the array.
In the average case, the target value is somewhere in the
array.
• In fact, since the target value can be anywhere in the
array, any element of the array is equally likely.
• So on average, the target value will be in the middle of the
array.
• So the search takes an amount of time proportional to
half the length of the array

9. Divide
and
Conquer
The most well known algorithm design
strategy:
• Divide the problem into two or more
smaller subproblems.
• Conquer the subproblems by solving
them recursively.
• Combine the solutions to the
subproblems into the solutions for the
original problem.

10. THE
DIVIDE
AND
CONQUER
ALGORITHM

11. Divide
and
Conquer:
Merge Sort
The merge sort algorithm works from “the bottom up”
• start by solving the smallest pieces of the main problem
• keep combining their results into larger solutions
• eventually the original problem will be solved
Sort into nondecreasing order
[25][57][48][37][12][92][86][33]
pass 1
[25 57][37 48][12 92][33 86]
pass 2
[25 37 48 57][12 33 86 92]
pass 3
[12 25 33 37 48 57 86 92]
• log2n passes are required.
• time complexity: O(nlogn)

12. Strassen’s
Matrix
Multiplication
• Strassen showed that 2x2 matrix multiplication can be
accomplished in 7 multiplication and 18 additions or
subtractions. .(2log
2
7 =22.807)
• This reduce can be done by Divide and
Conquer Approach.

13. Strassen’s
Matrix
Multiplication
(Cont…)
P1 = (A11+ A22)(B11+B22)
P2 = (A21 + A22) * B11
P3 = A11 * (B12 - B22)
P4 = A22 * (B21 - B11)
P5 = (A11 + A12) * B22
P6 = (A21 - A11) * (B11 + B12)
P7 = (A12 - A22) * (B21 +B22)
C11 = P1 + P4 - P5 + P7
C12 = P3 +P5
C21 = P2 + P4
C22 = P1 + P3 - P2 + P6

14. Strassen’s
Matrix
Multiplication:
Analysis
n 2
(n2
) n 2T (n) 7T
n
2
b
f (n)Com pare above rec urrenc ew ith T (n) aT
n
b
n2
n2.81
nlog 2 7
O(n2.81
)
a 7, b 2 f(n)
nlog b a
T (n)

15. Strassen’s
Matrix
Multiplication:
Time Analysis

16. Analysis
of
Binary
Search
The general term for a smart search through sorted data
is a binary search.
• The initial search region is the whole array.
• Look at the data value in the middle of the search
region.
• If you’ve found your target, stop.
• If your target is less than the middle data value, the
new search region is the lower half of the data.
• If your target is greater than the middle data value, the
new
• search region is the higher half of the data.
• Continue from Step 2.

17. Binary
Search
Example
low
Searching for 18.
middle high
-86 -37 -23 0 5 18 21 64 97
-86 -37 -23 0 5 18 21 64 97
low middle high
-86 -37 -23 0 5 18 21 64 97
low
middle
high

18. Analysis
of
Binary
Search:
Time
Complexity
• How fast is binary search?
• Think about how it operates: after you examine a
value, you cut the search region in half.
• So, the first iteration of the loop, your search region is
the whole
• array.
• The second iteration, it’s half the array.
• The third iteration, it’s a quarter of the array.
• ...
• The kth iteration, it’s (1/2k-1) of the array.
• Binary search only works if the array is already sorted.
• It turns out that sorting is a huge issue in computing

19. Decrease
and
Conquer
 Exploring the relationship between a solution to a given instance of
(e.g., P(n) )a problem and a solution to a smaller instance (e.g.,
P(n/2) or P(n-1) )of the same problem.
 Use top down(recursive) or bottom up (iterative) to
solve the problem.
 Example, n!
 A top down (recursive) solution
 A bottom up (iterative) solution
 Decrease by a constant: the size of the problem is reduced by the same constant on each
iteration/recursion of the algorithm.
 Insertion sort
 Graph search algorithms:
 DFS
 BFS
 Topological sorting
 Algorithms for generating permutations, subsets
 Decrease by a constant factor: the size of the problem is reduced by the same constant factor on each
iteration/recursion of the algorithm.
 Binary search
 Fake-coin problems
 Variable-size decrease: the size reduction pattern varies from one iteration of an algorithm to another.
 Euclid’s algorithm

20. A Typical
Decrease by
a Constant
Factor
(half)
Technique
subproblem
of size n/2
a solution to the
subproblem
a problem of size n
a solution to
the original problem
e.g., Binary search