Download to read offline
![# Import libraries --------------------------------------------------------
library(ggplot2)
library(car)
library(MASS)
library(ggfortify)
library(tree)
library(randomForest)
# Import Data -------------------------------------------------------------
Smartphones <- read.csv("train.csv") # dataset scaricabile da kaggle.com al seguente indirizzo:
https://www.kaggle.com/iabhishekofficial/mobile-price-classification#train.csv
str(Smartphones)
# Variables manipulations -------------------------------------------------
## Transform int variables in factors
Smartphones$blue <- as.factor(Smartphones$blue)
Smartphones$dual_sim <- as.factor(Smartphones$dual_sim)
Smartphones$four_g <- as.factor(Smartphones$four_g)
Smartphones$three_g <- as.factor(Smartphones$three_g)
Smartphones$touch_screen <- as.factor(Smartphones$touch_screen)
Smartphones$wifi <- as.factor(Smartphones$wifi)
Smartphones$price_range <- factor(Smartphones$price_range, levels = c(0,1,2,3), labels =
c("Low","Medium", "High", "Very High"))
str(Smartphones)
summary(Smartphones)
# Cross Validation --------------------------------------------------------
set.seed(1)
train <- sample(2000, 1333)
train
## Dataset test 667 observations
Smartphones_test <- Smartphones[-train,] # dataset test composto da 1/3 delle osservazioni
nrow(Smartphones_test)
## Dataset train 1333 observations
Smartphones_train <- Smartphones[train,] # dataset train composto da 2/3 delel osservazioni
nrow(Smartphones_train)
# LDA ---------------------------------------------------------------------
lda_0 <- lda(price_range ~ ., data = Smartphones_train) # LDA utilizzando tutte le variabili del dataset
lda_0
lda_0_pred <- predict(lda_0, Smartphones_test) # predizione delle osservazioni del dataset test
lda_Smartphones <- data.frame(Smartphones_test, "pred. price_range"=lda_0_pred$class, "post.
prob"=round(lda_0_pred$posterior, digits = 4))
addmargins(table(lda_Smartphones$pred..price_range, lda_Smartphones$price_range))
test_error_lda <- (1+6+9+3+6+1)/nrow(Smartphones_test) # test error della lda
test_error_lda
# Trees -------------------------------------------------------------------
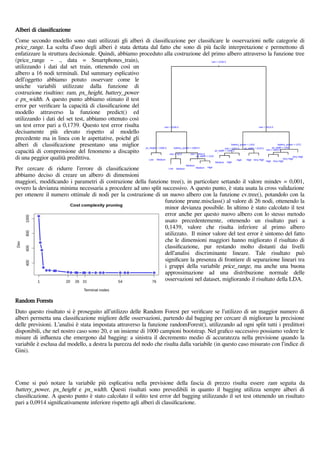
tree_Smartphones <- tree(price_range ~ ., data = Smartphones_train) # albero di classificazione
utilizzando tutte le variabili del dataset
tree_Smartphones
summary(tree_Smartphones)
## plot
plot(tree_Smartphones, lwd=2) # plot dell'albero
text(tree_Smartphones,pretty = 0,cex=0.9,col="blue")
## prediction using set Test
# predict class
tree_Smartphones_pred <- predict(tree_Smartphones, Smartphones_test, type = "class")
# predict probability
tree_Smartphones_pred_prob <- round(predict(tree_Smartphones, Smartphones_test), digits=4)](https://image.slidesharecdn.com/mobilepriceclassification-190225175855/85/Mobile-price-classification-5-320.jpg)
![rf_Smartphones <- randomForest(price_range ~ ., data = Smartphones_train, mtry = 4, importance=T,
ntree=1000) #foresta casuale, uso mtry=4 poichè faccio radice quadrata dei predittori, 1000 campioni
bootstrap
rf_Smartphones
importance(rf_Smartphones)
varImpPlot(rf_Smartphones, lwd=1, ce=0.9, col="blue") # importance plot per verificare quali variabili
sono più esplicative
## test error Random forest
rf_pred <- predict(rf_Smartphones, Smartphones_test, type = "class")
addmargins(table(Smartphones_test$price_range, rf_pred))
test.error.rf <- (10+9+11+21+10+10)/nrow(Smartphones_test) # test error random forest
test.error.rf
## Comparison between test errors of the models
print(c(test_error_lda, test.error.tree, test.error.prunetree, test.error.bag,test.error.rf )) #
comparazione tra i test error dei vari modelli utilizzati, LDA preferibile
data.frame(row.names = c("lda", "tree", "pruned tree", "bagging", "random forest"), "Test
error"=c(test_error_lda, test.error.tree, test.error.prunetree, test.error.bag,test.error.rf))
# PCA ---------------------------------------------------------------------
pca <- Smartphones[, -c(2,3,4,5,6,7,8,9,10,11,12,15,16,17,18,19,20)] #creo dataset con solo variabili più
significative emerse dai modelli precedenti
pca$price_range <- as.integer(pca$price_range) # trasformo variabile price_range in integer per poter
utilizzare PCA
pr_out <- prcomp(pca[,-4], scale = T) # uso funzione per la PCA
head(pca)
summary(pr_out)
pca$price_range<-factor(pca$price_range, c(1,2,3,4), c("Low","Medium","High","Very High")) # trasformo
price_range nuovamente in factor per effettuare il plot
autoplot(pr_out, data=pca, size=1, colour="price_range", loadings=TRUE, loadings.label=TRUE) # plot della
PCA
# Linear regression -------------------------------------------------------
### dipendent variable Ram
reg_ram <- lm(ram ~ ., data = Smartphones_train) # regressione lineare multipla con tutte le variabili
per stimare ram
summary(reg_ram)
vif(reg_ram) # verifico multicollinearità con il variance inflation ratio
reg_ram_price <- lm(ram ~ price_range, data = Smartphones_train) # regressione lineare semplice con solo
price_range come variabile indipendente
summary(reg_ram_price)
reg_ram_mobile_wt <- lm(ram ~ mobile_wt, data = Smartphones_train) #regressione lineare semplice con solo
mobile_wt come variabile indipendente
summary(reg_ram_mobile_wt)
reg_ram_dual_sim <- lm(ram ~ dual_sim, data = Smartphones_train) #regressione lineare semplice con solo
dual_sim come variabile indipendente
summary(reg_ram_dual_sim)
reg_ram_battery_power <- lm(ram ~ battery_power, data = Smartphones_train) #regressione lineare semplice
con solo battery_power come variabile indipendente
summary(reg_ram_battery_power)
reg_ram_px <- lm(ram ~ px_height, data = Smartphones_train) #regressione lineare semplice con solo
px_height come variabile indipendente
summary(reg_ram_px)
### dipendent variable battey power
reg_battery <- lm(battery_power ~ ., data = Smartphones_train) # regressione lineare multipla con tutte
le variabili per stimare battery_power
summary(reg_battery)](https://image.slidesharecdn.com/mobilepriceclassification-190225175855/85/Mobile-price-classification-7-320.jpg)
Mobile price classification
- 1. Mirco Barbero 203137,Alessandra Bellofiore 206014, Christian Isgrò 205632 Progetto Strumenti Quantitativi per la Gestione – Caratteristiche Smartphones Il dataset che abbiamo deciso di analizzare riguarda le caratteristiche tecniche di smartphones di diversi produttori. Sono state raccolte 21 variabili, quantitative e qualitative, per 2000 osservazioni: - Id: ID - Battery_power: l’energia totale che una batteria può contenere per volta - Blue: se è dotato di Bluetooth o no - Clock_speed: la velocità alla quale il microprocessore esegue le istruzioni - Dual_sim: se è dotato di due supporti per le sim o no - Fc: Fotocamera frontale in megapixel - Four_g: se è dotato di 4G o no - Int_memory: Memoria interna in gigabytes - M_dep: Spessore dello smartphone in cm - Mobile_wt: peso del mobile phone - N_cores: numero di core del processore - Pc: fotocamera principale in megapixel - Px_height: Risoluzione dei pixel in base all’altezza - Px_width: risoluzione dei pixel in base all’ampiezza - Ram: random access memory in megabytes - Sc_h: altezza dello schermo del cellulare in centimetri - Sc_w: ampiezza dello schermo del cellulare in centimetri - Talk_time: periodo di tempo in cui una singola batteria carica può durare con il telefono attivo - Three_g: se il cellulare è dotato di 3G o no - Touch_screen: se il cellulare è dotato di touch screen o no - Wifi: se il cellulare è dotato di wi-fi o no Sono state utilizzate tutte le variabili, in quanto a nostro avviso contribuiscono a dare un apporto al fenomeno. L’obiettivo di questa analisi è far comprendere alle imprese se lo smartphone da loro offerto, sulla base delle caratteristiche analizzate, rientri nella giusta fascia di prezzo. Può essere utilizzato anche dai consumatori per comprendere se lo smartphone da loro acquistato rientri nella giusta categoria. Manipolazione variabili Prima di cominciare l’analisi, le variabili quantitative del dataset sono state modificate in factor, in quanto come dati qualitativi, rendono più facile l’interpretazione. Queste sono: Bluetooth, Dual_sim, Four_g, Three_g, Touch_screen, Wifi, Price_range. Cross Validazione Successivamente, il dataset è stato suddiviso in un set training e in un set test con una proporzione rispettivamente di 2/3 e 1/3 in modo da poter testare i modelli che andremo a sviluppare. Questi dati sono stati analizzati utilizzando le seguenti tecniche: - LDA - Alberi di classificazione - Foreste casuali - Regressione lineare Classificazione L’analisi su cui ci siamo focalizzati è stata la classificazione delle osservazioni nelle categorie della variabile qualitativa price_range. A riguardo abbiamo utilizzato dei modelli che ci hanno permesso di raggiungere questo risultato valutandoli in base al valore di test error ottenuto da ognuno. LDA Come primo modello è stata utilizzata l’analisi discriminante lineare, la quale attraverso il teorema di Bayes produce stime sull’appartenenza di una variabile risposta qualitativa ad una certa categoria. Abbiamo preferito tale modello alla regressione logistica poiché il numero di classi della nostra variabile risposta sono maggiori di due: “Low”; “Medium”; “High”; “Very High”. Dall’analisi effettuata otteniamo un test error del modello pari a 0,0389 (dato da (1+6+9+3+6+1)/667). In questo caso, non sono stati calcolati i valori di sensitività e specificità poiché avendo quattro livelli della variabile qualitativa, il calcolo dei valori veri positivi e falsi positivi non risultava agevole, da qui la mancanza del grafico della curva ROC.
- 2. Alberi di classificazione Comesecondo modello sono stati utilizzati gli alberi di classificazione per classificare le osservazioni nelle categorie di price_range. La scelta d’uso degli alberi è stata dettata dal fatto che sono di più facile interpretazione e permettono di enfatizzare la struttura decisionale. Quindi, abbiamo proceduto alla costruzione del primo albero attraverso la funzione tree (price_range ~ ., data = Smartphones_train), utilizzando i dati dal set train, ottenendo così un albero a 16 nodi terminali. Dal summary esplicativo dell’oggetto abbiamo potuto osservare come le uniche variabili utilizzate dalla funzione di costruzione risultino: ram, px_height, battery_power e px_width. A questo punto abbiamo stimato il test error per verificare la capacità di classificazione del modello attraverso la funzione predict() ed utilizzando i dati del set test, abbiamo ottenuto così un test error pari a 0,1739. Questo test error risulta decisamente più elevato rispetto al modello precedente ma in linea con le aspettative, poiché gli alberi di classificazione presentano una miglior capacità di comprensione del fenomeno a discapito di una peggior qualità predittiva. Per cercare di ridurre l’errore di classificazione abbiamo deciso di creare un albero di dimensioni maggiori, modificando i parametri di costruzione della funzione tree(), in particolare settando il valore mindev = 0,001, ovvero la devianza minima necessaria a procedere ad uno split successivo. A questo punto, è stata usata la cross validazione per ottenere il numero ottimale di nodi per la costruzione di un nuovo albero con la funzione cv.tree(), potandolo con la funzione prune.misclass() al valore di 26 nodi, ottenendo la minor devianza possibile. In ultimo è stato calcolato il test error anche per questo nuovo albero con lo stesso metodo usato precedentemente, ottenendo un risultato pari a 0,1439, valore che risulta inferiore al primo albero utilizzato. Il minor valore del test error è sintomo del fatto che le dimensioni maggiori hanno migliorato il risultato di classificazione, pur restando molto distanti dai livelli dell’analisi discriminante lineare. Tale risultato può significare la presenza di frontiere di separazione lineari tra i gruppi della variabile price_range, ma anche una buona approssimazione ad una distribuzione normale delle osservazioni nel dataset, migliorando il risultato della LDA. Random Forests Dato questo risultato si è proseguito all’utilizzo delle Random Forest per verificare se l’utilizzo di un maggior numero di alberi permetta una classificazione migliore delle osservazioni, partendo dal bagging per cercare di migliorare la precisione delle previsioni. L’analisi è stata impostata attraverso la funzione randomForest(), utilizzando ad ogni split tutti i predittori disponibili, che nel nostro caso sono 20, e un insieme di 1000 campioni bootstrap. Nel grafico successivo possiamo vedere le misure di influenza che emergono dal bagging: a sinistra il decremento medio di accuratezza nella previsione quando la variabile è esclusa dal modello, a destra la purezza del nodo che risulta dalla variabile (in questo caso misurato con l’indice di Gini). Come si può notare la variabile più esplicativa nella previsione della fascia di prezzo risulta essere ram seguita da battery_power, px_height e px_width. Questi risultati sono prevedibili in quanto il bagging utilizza sempre alberi di classificazione. A questo punto è stato calcolato il solito test error del bagging utilizzando il set test ottenendo un risultato pari a 0,0914 significativamente inferiore rispetto agli alberi di classificazione.
- 3. In conclusione, poichéil bagging, utilizzando tutti i predittori del dataset per la costruzione degli alberi ad ogni split, tende ad aumentare la varianza, abbiamo provato ad utilizzare una foresta casuale con √p (nel nostro caso √20 = 4) predittori casuali ad ogni split. Con la funzione randomForest() impostiamo l’analisi sempre su 1000 campioni bootstrap. Anche in questo caso la variabile più esplicativa risulta essere ram e anche le misure di influenza risultano simili a quelle del bagging, mentre la stima dell’errore Out-Of-Bag risulta essere maggiore rispetto a quella del bagging. È stato stimato ancora una volta il test error per poterlo comparare con gli altri modelli. Abbiamo ottenuto un risultato di 0,1064, il quale è più elevato rispetto al test error bagging, nonostante ci aspettassimo un risultato inferiore. A termine dell’analisi abbiamo potuto constatare come il metodo migliore per la classificazione risulti essere l’analisi discriminante lineare poiché presenta un test error nettamente inferiore rispetto agli altri modelli. Nonostante ciò, tale modello non è di facile interpretazione, in quanto non dà informazioni su quali variabili abbiano una maggiore capacità di spiegazione del fenomeno osservato. Tuttavia, per il singolo problema di classificazione rimane il preferibile. PCA Per ottenere una verifica e possibile spiegazione dei risultati ottenuti, abbiamo deciso di inserire a conclusione dell’analisi di classificazione un modello di componenti principali (PCA). Tale modello è stato costruito utilizzando le variabili maggiormente esplicative emerse dai modelli precedenti. Ciò che risulta è una forte stratificazione delle osservazioni della variabile price_range, come emerge anche dalla distribuzione dei dati nel dataset. La variabile che meglio spiega la divisione in classi risulta ancora ram come già evidenziato precedentemente dagli altri modelli. Tale divisione netta dei gruppi può aver determinato il miglior risultato di classificazione del modello LDA, rispetto ad alberi di classificazione e foreste. Regressioni lineari Una volta conclusa l’analisi di classificazione ci siamo brevemente concentrati sulle variabili quantitative del modello, in particolare quelle messe in risalto dai modelli precedenti per la loro capacità predittiva del price_range. Quindi, attraverso dei modelli di regressione lineare abbiamo voluto verificare se e come queste variabili venissero influenzate. La prima variabile analizzata è stata ram. Attraverso la formula lm() abbiamo costruito un modello di regressione lineare multiplo inserendo come predittori tutte le variabili del dataset, sia qualitative che quantitative. In particolare, dall’analisi risultano significative: battery_power, dual_sim, mobile_wt, px_height, px_width e price_range. Anche il valore p-value della statistica F risulta significativo, determinando capacità predittiva del modello. Inoltre, il valore R2 indica una buona approssimazione lineare dei dati con un valore di 0.9108. Anche il valore di R2 aggiustato 0.9093 risulta in linea, sintomo
- 4. che l’alto numerodi predittori non ha penalizzato la statistica. A seguito della regressione multipla abbiamo verificato la presenza di multicollinearità nei dati per evitare un overfitting del modello. Si è quindi utilizzata la funzione vif() ovvero il variance inflation factor che mette a rapporto la varianza dei coefficienti nel modello multiplo con il loro corrispettivo in un modello semplice. Sono stati ottenuti tutti valori inferiori a 10, sintomo che la multicollinearità può essere ignorata. In merito all’effetto delle variabili possiamo notare che solo il price_range influenza significativamente l’aumento della ram. Nello specifico ogni fascia di prezzo genera un incremento di circa 1 gigabyte. Per completezza abbiamo eseguito delle regressioni lineari semplici con le variabili che sono risultate significative nella regressione multipla. Si è notato che solamente la variabile price_range risulta non influenzata dalle altre, mantenendo la propria significatività. Si è svolto lo stesso procedimento con le variabili battery_power e talk_time come variabili dipendenti ottenendo risultati non significativi con valori di p-value della statistica F elevati e multicollinearità di alcune variabili. Dunque, è stato deciso di non proseguire con l’analisi di tali variabili attraverso questo modello. Per ultimo si è costruito un modello lineare per verificare l’esistenza di relazione tra fotocamera principale e fotocamera frontale. Prendendo come dipendente la prima otteniamo dai dati che la seconda risulta significativa sia nel modello multiplo che in quello singolo. Il risultato è un rapporto incrementale 1:1 megapixel tra le due fotocamere. Di seguito il plot che descrive le due variabili e la retta di regressione stimata dal nostro modello. Conclusione L’analisi svolta permette di ottenere un modello ottimale per la classificazione delle osservazioni, attraverso il quale si evince se lo smartphone venduto dai produttori è collocato nella giusta fascia di prezzo, o se i consumatori hanno pagato la giusta fascia di prezzo. Per comprenderlo sono stati utilizzati vari modelli: LDA, alberi di classificazione, bagging e foreste casuali. Dall’analisi è emerso che il modello migliore è la LDA, in quanto presenta un test error inferiore rispetto gli altri. Nonostante ciò, questa non è in grado di fornire ulteriori informazioni sul fenomeno, come ad esempio gli alberi di classificazione, i quali ci hanno permesso di capire come la ram sia la variabile che influenza maggiormente il price_range. Ad ogni modo, per il solo obiettivo di classificazione la LDA risulta essere il modello preferibile. Infine, si è analizzato con modelli di regressione lineare come vengano influenzate le variabili quantitative enfatizzate dai precedenti modelli di classificazione. In particolare si è potuto osservare come la ram incrementi in base alla fascia di prezzo degli smartphones. Inoltre, è stato possibile stimare una relazione tra la fotocamera principale e secondaria notando come queste incrementino proporzionalmente.
- 5.
- 6.
- 7.
- 8.