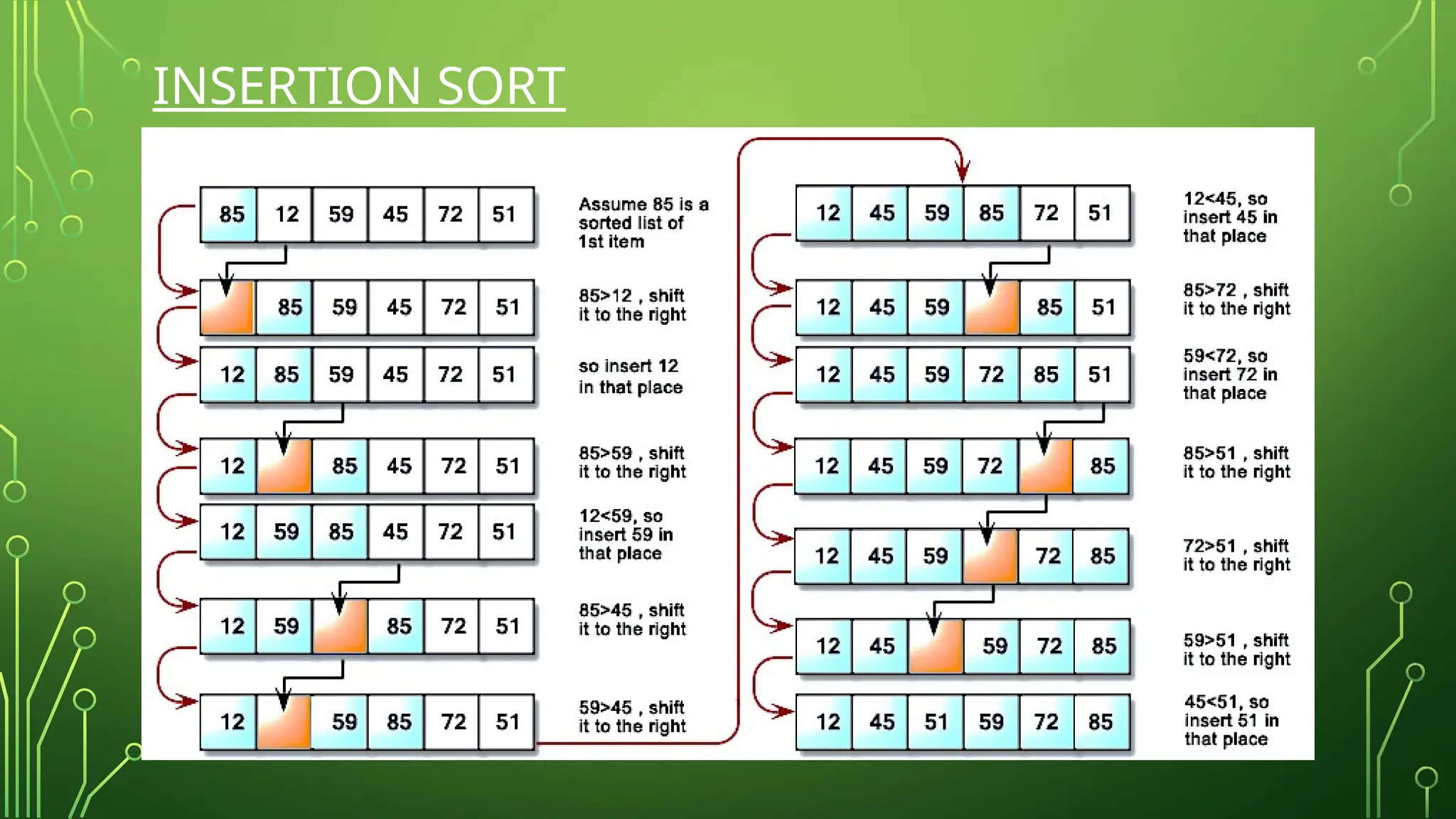
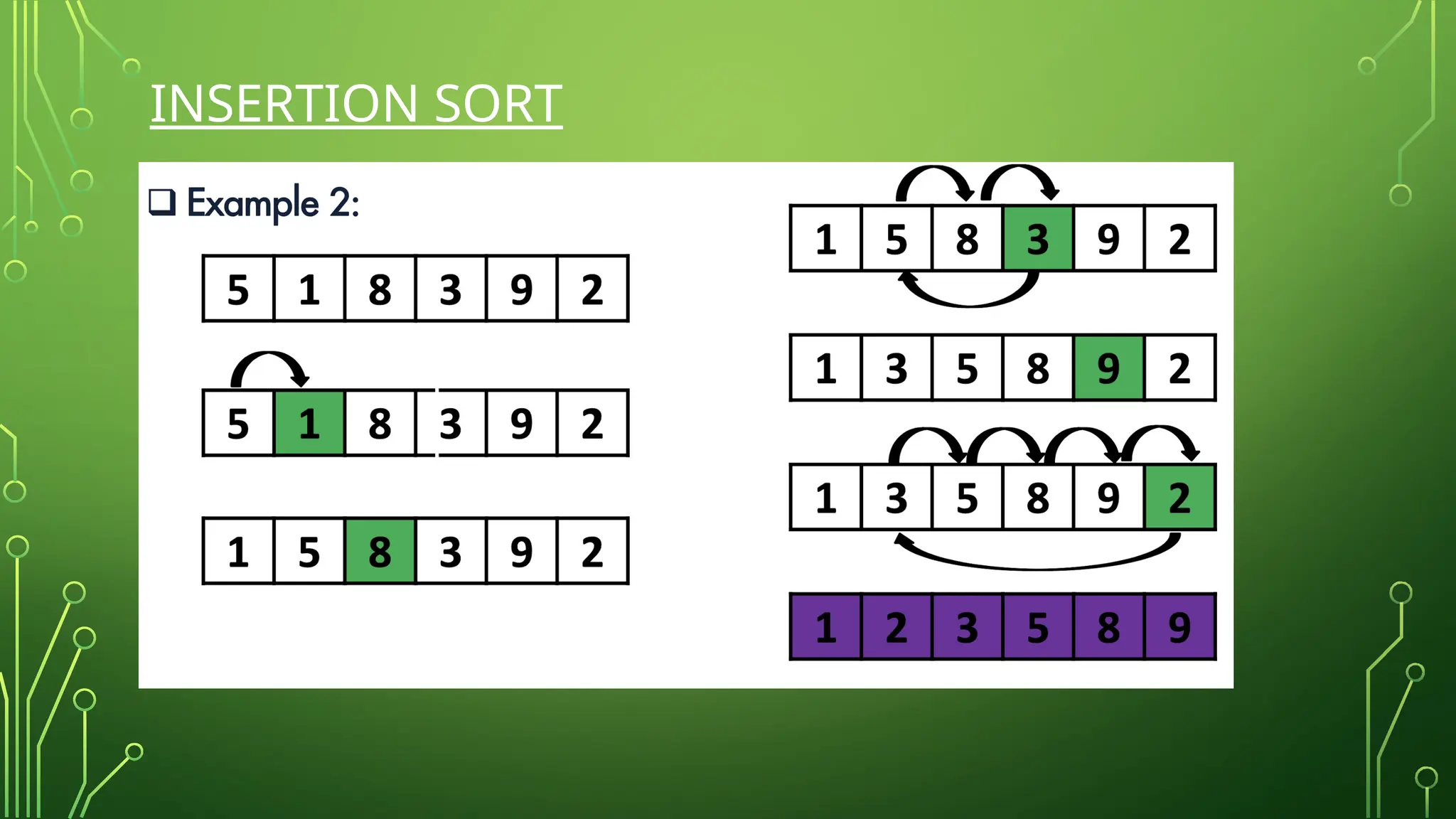
Dokumen ini menjelaskan algoritma pencarian dan pengurutan dalam ilmu komputer. Ia membahas metode seperti pencarian linier dan biner, serta berbagai algoritma pengurutan seperti bubble sort, selection sort, dan insertion sort, bersama dengan analisis kompleksitas waktu untuk masing-masing. Informasi ini penting untuk memahami bagaimana data dapat diambil dan diatur secara efisien dalam struktur data.

1. PENCARIAN & PENGURUTAN

2. PENCARIAN (SEARCHING)
• Dalam ilmu komputer, pencarian (searching) adalah proses
menemukan item dengan properti tertentu dari kumpulan item. Item
dapat disimpan sebagai catatan dalam database, elemen data
sederhana dalam array, teks dalam file, simpul dalam pohon, simpul
dan tepi dalam grafik, atau elemen ruang pencarian lainnya.
• Saat ini komputer dapat menyimpan informasi dengan jumlah cukup
besar. Untuk mengambil informasi ini dengan cepat, dibutuhkan
algoritma pencarian yang efisien

3. ALGORITMA PENCARIAN (SEARCHING)
• serangkaian langkah atau instruksi yang digunakan untuk
menemukan data tertentu dalam suatu struktur data
scholarhat.c

4. ALGORITMA PENCARIAN (SEARCHING
ALGORITHMS)
• Pencarian Beruntun/Linier
(data tidak harus terurut)
• Pencarian Biner
(data terurut)
https://favtutor.com/blogs/searching-algorithms

5. PENCARIAN LINIER (LINEAR/SEQUENTIAL
SEARCHING)
• Algoritma ini mencari elemen dengan memeriksa setiap elemen
dalam struktur data satu per satu hingga elemen yang dicari
ditemukan atau seluruh elemen telah diperiksa
• Keuntungan: Sederhana dan mudah diimplementasikan
• Kelemahan: Tidak efisien untuk struktur data tidak linear atau
data besar

6. ALGORITMA SEQUENTIAL SEARCH
(UNORDERED)
• Step 1 : Telusuri setiap elemen array menggunakan for loop.
• Step 2 : Di setiap iterasi for loop, bandingkan elemen pencarian
dengan elemen array saat ini, dimana :
• Jika elemennya cocok, maka kembalikan indeks dari elemen array
yang sesuai.
• Jika elemen tidak cocok, pindah ke elemen berikutnya.
• Step 3 : Jika tidak ada kecocokan atau elemen pencarian tidak ada
dalam larik yang diberikan, kembalikan nilai -1

7. SEQUENTIAL SEARCH
(UNORDERED)
• Algoritma Sequential Search :
• Step 1 : Telusuri setiap elemen array menggunakan
for loop.
• Step 2 : Di setiap iterasi for loop, bandingkan elemen
pencarian dengan elemen array saat ini, dimana :
• Jika elemennya cocok, maka kembalikan indeks
dari elemen array yang sesuai.
• Jika elemen tidak cocok, pindah ke elemen
berikutnya.
• Step 3 : Jika tidak ada kecocokan atau elemen
pencarian tidak ada dalam larik yang diberikan,
kembalikan nilai -1
• Contoh Implementasi :
Array :
K : 41

8. SEQUENTIAL SEARCH
(UNORDERED)
• Kode Python untuk Sequential Search :
• Contoh Implementasi :
i=0 :
i=1 :
i=2 :
i=3 :
i=4 :
i=5 :

9. SEQUENTIAL SEARCH (UNORDERED)
• Kompleksitas Algoritma Seqential Search
• Best case :
• Best case terjadi ketika elemen yang kita temukan berada di posisi pertama dari array.
• Kompleksitas waktu kasus terbaik dari pencarian linear adalah O(1).
• Average case :
• Kompleksitas waktu kasus rata-rata dari pencarian linear adalah O(n).
• Worst case :
• Worst case terjadi ketika elemen yang kita cari ada di akhir array atau elemen target tidak ada
dalam larik yang diberikan, sehingga kita harus melintasi seluruh larik.
• Kompleksitas waktu kasus terburuk dari pencarian linear adalah O(n).

10. SEQUENTIAL SEARCH (ORDERED)
• Jika elemen-elemen dari array sudah diurutkan, maka dalam banyak kasus kita tidak perlu memindai
seluruh array untuk melihat apakah elemen tersebut ada di dalam array yang diberikan atau tidak.
• Pada algoritma Sequential Search di bawah ini, dapat dilihat bahwa, kapan saja jika nilai pada A[i] lebih
besar dari data yang akan dicari, maka kita hanya mengembalikan -1 tanpa mencari di array yang tersisa.
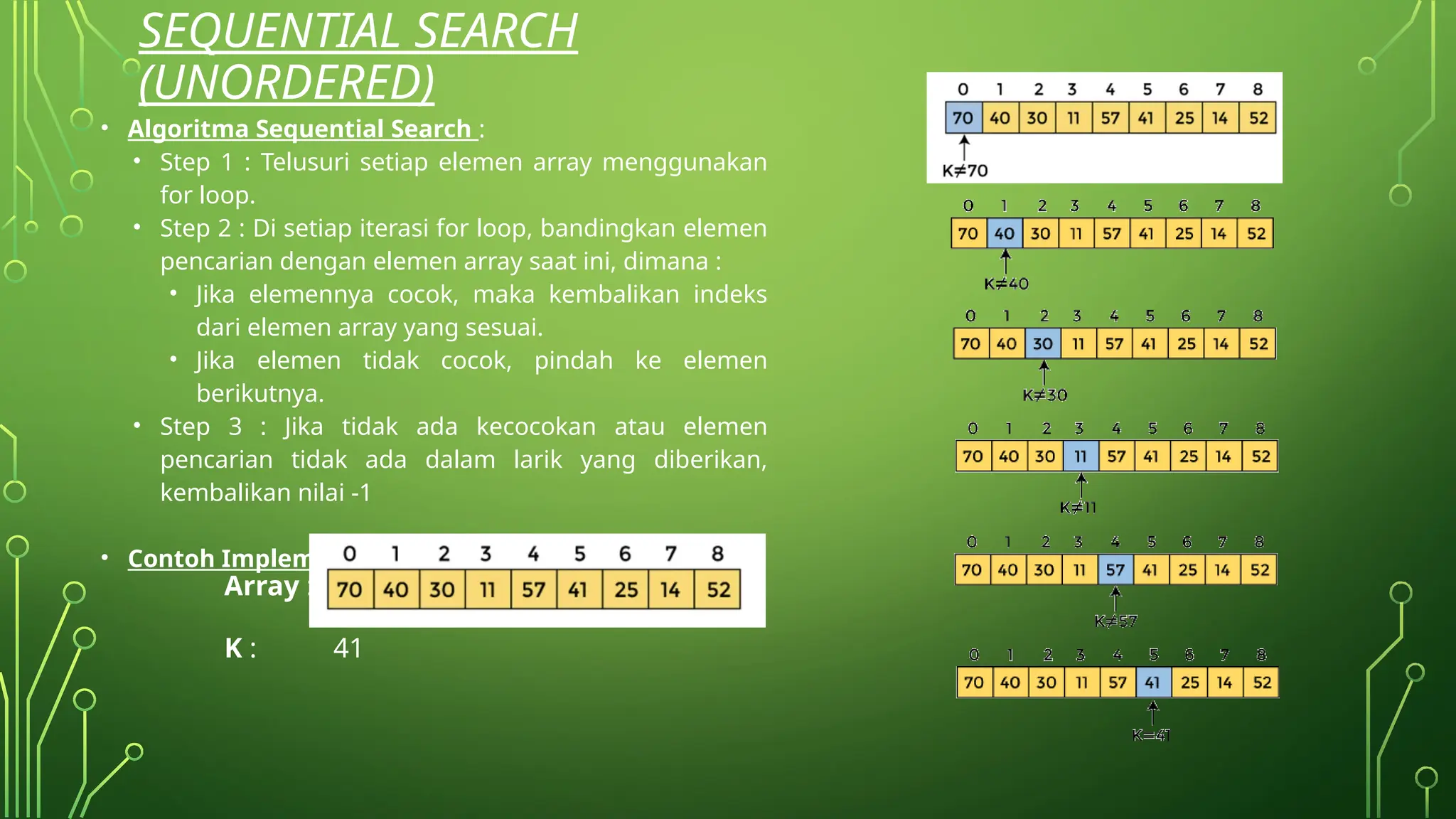
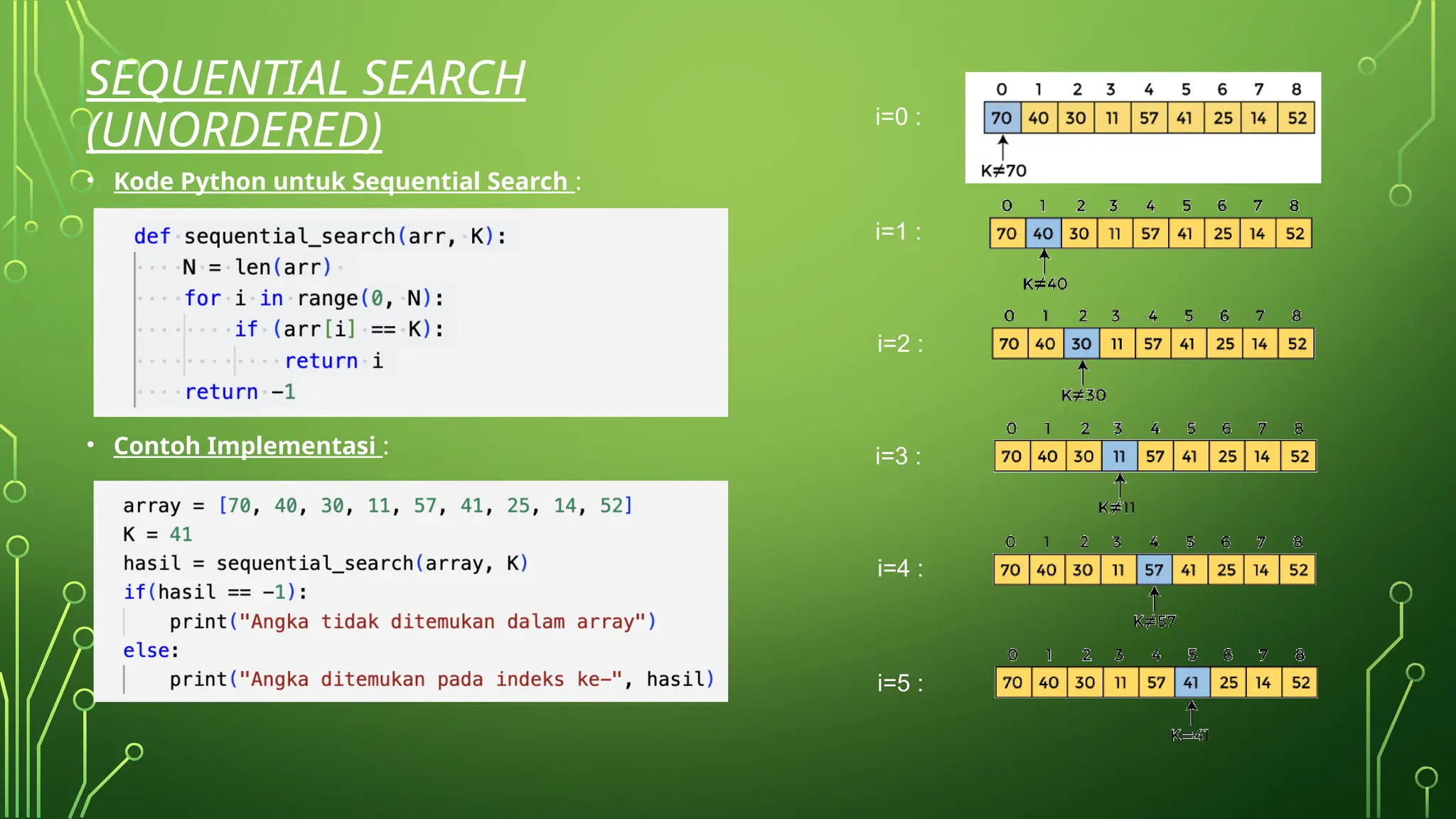
• Algoritma Sequential Search (Ordered) :
• Step 1 : Telusuri setiap elemen array menggunakan for loop.
• Step 2 : Di setiap iterasi for loop, bandingkan elemen pencarian dengan elemen array saat ini, dimana
:
• Jika elemennya cocok, maka kembalikan indeks dari elemen array yang sesuai.
• Jika elemen tidak cocok, pindah ke elemen berikutnya.
• Jika elemen saat ini > elemen pencarian, maka kembalikan nilai -1
• Step 3 : Jika tidak ada kecocokan atau elemen pencarian tidak ada dalam array yang diberikan,
kembalikan nilai -1

11. SEQUENTIAL SEARCH (ORDERED)
• Algoritma Sequential Search :
• Step 1 : Telusuri setiap elemen array menggunakan
for loop.
• Step 2 : Di setiap iterasi for loop, bandingkan elemen
pencarian dengan elemen array saat ini, dimana :
• Jika elemennya cocok, maka kembalikan indeks
dari elemen array yang sesuai.
• Jika elemen tidak cocok, pindah ke elemen
berikutnya.
• Jika elemen saat ini > elemen pencarian, maka
kembalikan nilai -1
• Step 3 : Jika tidak ada kecocokan atau elemen
pencarian tidak ada dalam larik yang diberikan,
kembalikan nilai -1
• Contoh Implementasi :
Array :
K : 35
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
40 > K
return -1

12. SEQUENTIAL SEARCH (ORDERED)
• Kode Python untuk Sequential Search :
• Contoh Implementasi :
i=0 :
i=1 :
i=2 :
i=3 :
i=4 :
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
0 1 2 3 4 5 6 7 8
11 14 25 30 40 41 52 57 70
return -1

13. SEQUENTIAL SEARCH (ORDERED)
• Kompleksitas Algoritma Seqential Search
• Best case :
• Best case terjadi ketika elemen yang kita temukan berada di posisi pertama dari array.
• Kompleksitas waktu kasus terbaik dari pencarian linear adalah O(1).
• Average case :
• Kompleksitas waktu kasus rata-rata dari pencarian linear adalah O(n).
• Worst case :
• Worst case terjadi ketika elemen yang kita cari ada di akhir array atau elemen target tidak ada
dalam larik yang diberikan, sehingga kita harus melintasi seluruh larik.
• Kompleksitas waktu kasus terburuk dari pencarian linear adalah O(n).

14. BINARY SEARCH (ORDERED)
• Binary Search adalah pencarian di mana elemen tengah dihitung untuk memeriksa apakah
lebih kecil atau lebih besar dari elemen yang akan dicari.
• Pencarian biner mengikuti pendekatan divide dan conquer di mana daftar dibagi menjadi
dua bagian, dan item dibandingkan dengan elemen tengah daftar. Jika kecocokan ditemukan,
lokasi elemen tengah dikembalikan. Kalau tidak, kami mencari di salah satu bagian
tergantung pada hasil yang dihasilkan selama perbandingan.
• Algoritma Binary Search bekerja secara efisien pada array yang terurut.

15. BINARY SEARCH (ORDERED)
• Algoritma Binary Search:
• Step 1 : Urutkan array dalam urutan ascending (menaik).
• Step 2 : Setel indeks elemen pertama array sebagai low dan indeks elemen terakhir array
sebagai high.
• Step 3 : Tetapkan indeks mid dengan nilai dari rata-rata indeks low dan high.
• Step 4 : Lakukan perbandingan, dimana:
• Jika elemen di indeks mid adalah elemen target, kembalikan indeks mid.
• Jika elemen target lebih kecil dari elemen di indeks mid, Lakukan Binary Search
dengan indeks high menjadi indeks mid – 1 (mencari di sisi tengah sebelah kiri)
• Jika elemen target lebih besar dari elemen di indeks mid, Lakukan Binary Search
dengan indeks low menjadi indeks mid + 1 (mencari di sisi tengah sebelah kanan)
• Jika elemen tidak ada di dalam array, kembalikan nilai -1.

16. BINARY SEARCH (ORDERED)
• Algoritma Binary Search :
• Step 1 : Urutkan array dalam urutan ascending
(menaik).
• Step 2 : Setel indeks elemen pertama array sebagai
low dan indeks elemen terakhir array sebagai high.
• Step 3 : Tetapkan indeks mid dengan nilai dari rata-
rata indeks low dan high.
• Step 4 : Lakukan perbandingan, dimana:
• Jika elemen di indeks mid adalah elemen
target, kembalikan indeks mid.
• Jika elemen target lebih kecil dari elemen di
indeks mid, Lakukan Binary Search dengan
indeks high menjadi indeks mid – 1 (mencari
di sisi tengah sebelah kiri)
• Jika elemen target lebih besar dari elemen di
indeks mid, Lakukan Binary Search dengan
indeks low menjadi indeks mid + 1 (mencari di
sisi tengah sebelah kanan)
• Jika elemen tidak ada di dalam array, kembalikan
nilai -1.
Array :
K : 56
Contoh Implementasi :

17. BINARY SEARCH (ORDERED)
• Kode Python untuk Binary Search :
‘
• Contoh Implementasi :
Array :
K : 56

18. BINARY SEARCH (ORDERED)
• Kompleksitas Algoritma Binary Search
• Best case :
• Dalam Binary Search, kasus terbaik terjadi ketika elemen yang akan dicari ditemukan dalam
perbandingan pertama, yaitu ketika elemen tengah pertama itu sendiri adalah elemen yang akan
dicari. Kompleksitas waktu kasus terbaik dari pencarian Biner adalah O(1).
• Average case :
• Kompleksitas waktu kasus rata-rata dari pencarian biner adalah O(n).
• Worst case :
• Dalam pencarian Biner, kasus terburuk terjadi, ketika kita harus terus mengurangi ruang pencarian
hingga hanya memiliki satu elemen. Kompleksitas waktu kasus terburuk dari pencarian Biner
adalah O(logn).

19. • Sorting adalah algoritma yang mengatur elemen-elemen dari sebuah list
dalam urutan tertentu baik secara ascending maupun descending.
• Outputnya adalah permutasi atau penataan ulang input.
ALGORITMA PENGURUTAN (SORTING)
https://en.wikipedia.org/wiki/Insertion_sort

20. Why is Sorting Necessary?
• Sorting adalah salah satu
kategori penting dari algoritma
dalam ilmu komputer.
• Sorting dapat secara signifikan
mengurangi kerumitan dalam
suatu masalah, dan sering
digunakan untuk algoritma dan
pencarian basis data.
Gambar 1. Semua penerbangan yang memiliki kota tujuan yang sama diurutkan
berdasarkan jadwal keberangkatannya;

21. BUBBLE SORT
• Bubble sort adalah algoritma sorting yang paling sederhana.
• Algoritma “Bubble” Sort artinya elemen yang lebih kecil "menggelembung" ke bagian atas
array.
• Algoritma Bubble sort :
• Step 1 : Bandingkan setiap pasang elemen yang berdekatan dalam array
• Step 2: Tukar dua elemen jika perlu
• Step 3: Ulangi proses ini untuk semua elemen hingga seluruh array hingga terurut

22. BUBBLE SORT
40 2 1 43 3 65 0 -1 58 3 42 4
2 40 1 43 3 65 0 -1 58 3 42 4
2 40 1 43 3 65 0 -1 58 3 42 4
2 1 40 43 3 65 0 -1 58 3 42 4
2 1 40 43 3 65 0 -1 58 3 42 4
2 1 40 43 3 65 0 -1 58 3 42 4
2 1 40 3 43 65 0 -1 58 3 42 4
2 1 40 3 43 65 0 -1 58 3 42 4
2 1 40 3 43 65 0 -1 58 3 42 4
2 1 40 3 43 0 65 -1 58 3 42 4
2 1 40 3 43 0 65 -1 58 3 42 4
2 1 40 3 43 0 -1 65 58 3 42 4
2 1 40 3 43 0 -1 65 58 3 42 4
2 1 40 3 43 0 -1 58 65 3 42 4
2 1 40 3 43 0 -1 58 65 3 42 4
2 1 40 3 43 0 -1 58 3 65 42 4
2 1 40 3 43 0 -1 58 3 65 42 4
2 1 40 3 43 0 -1 58 3 42 65 4
2 1 40 3 43 0 -1 58 3 42 65 4
2 1 40 3 43 0 -1 58 3 42 4 65

23. BUBBLE SORT
• Perhatikan bahwa pada setiap iterasi, dapat dipastikan satu elemen akan menempati
tempat yang benar
40 2 1 43 3 65 0 -1 58 3 42 4
65
2 1 40 3 43 0 -1 58 3 42 4
65
58
1 2 3 40 0 -1 43 3 42 4
1 2 3 40
0 65
-1 43 58
3 42 4
1
2
3
4

24. BUBBLE SORT
1 0 -1 3
2 65
3 43 58
42
40
4
0 -1 1 2 65
3 43 58
42
40
4
3
-1 0 1 2 65
3 43 58
42
40
4
3
6
7
8
Berhenti di sini!
Mengapa?
1 2 0 3
-1 3 40 65
43 58
42
4
5

25. BUBBLE SORT
• Python Code :

26. BUBBLE SORT
• Running time:
• Worst case: O(n2
)
• Best case: O(n) – kapan? Mengapa?
• Variasi:
• Bi-directional bubble sort
• Original bubble sort: hanya bergerak ke satu arah
• Bi-directional bubble sort bergerak dua arah (bolak balik)

27. SELECTION SORT
• Selection Sort mengurutkan array dengan berulang
kali dengan menemukan elemen minimum (untuk
urutan ascending) dari bagian yang tidak disortir dan
meletakkannya di awal.
• Algoritma Selection Sort :
• Step 1: Temukan nilai minimum dalam array
• Step 2: Tukar dengan nilai di posisi saat ini
• Step 3: Ulangi proses ini untuk semua elemen
hingga seluruh array terurut

28. SELECTION SORT

29. SELECTION SORT

30. SELECTION SORT
• Running time:
• Worst case: O(n2
)
• Best case: O(n2
)
• Berdasarkan analisis big-oh, apakah selection sort lebih baik dari bubble
sort?
• Apakah running time yang sebenarnya merefleksikan analisis tersebut?

31. INSERTION SORT
• Insertion Sort adalah algoritma pengurutan sederhana yang berfungsi seperti cara kita
mengurutkan kartu remi
• Saat pemain mengambil kartu baru, pemain memberi ruang untuk kartu baru dan kemudian
memasukkannya ke tempat yang seharusnya.
• Jika kartu berikutnya adalah 8, itu harus disisipkan di antara 6 dan 10, menjaga urutan
numerik (diagram tengah). Jika kartu berikutnya adalah angka 7, maka harus disisipkan di
antara angka 6 dan 8 seperti yang ditunjukkan di sebelah kanan.

32. INSERTION SORT
• Algoritma Insertion Sort:
• Step 1: Bandingkan setiap pasang elemen yang berdekatan dalam array
• Step 2: Masukkan elemen ke dalam array yang terurut, hingga menempati posisi yang
benar.
• Step 3: Tukar dua elemen jika perlu
• Step 4: Ulangi proses ini untuk semua elemen sampai seluruh array diurutkan

33. INSERTION SORT

34. INSERTION SORT

35. INSERTION SORT

36. INSERTION SORT
• Running time analysis:
• Worst case: O(n2)
• Best case: O(n)
• Apakah insertion sort lebih cepat dari selection sort?
• Perhatikan persamaan dan perbedaan antara insertion sort dan selection
sort.
Simulasi