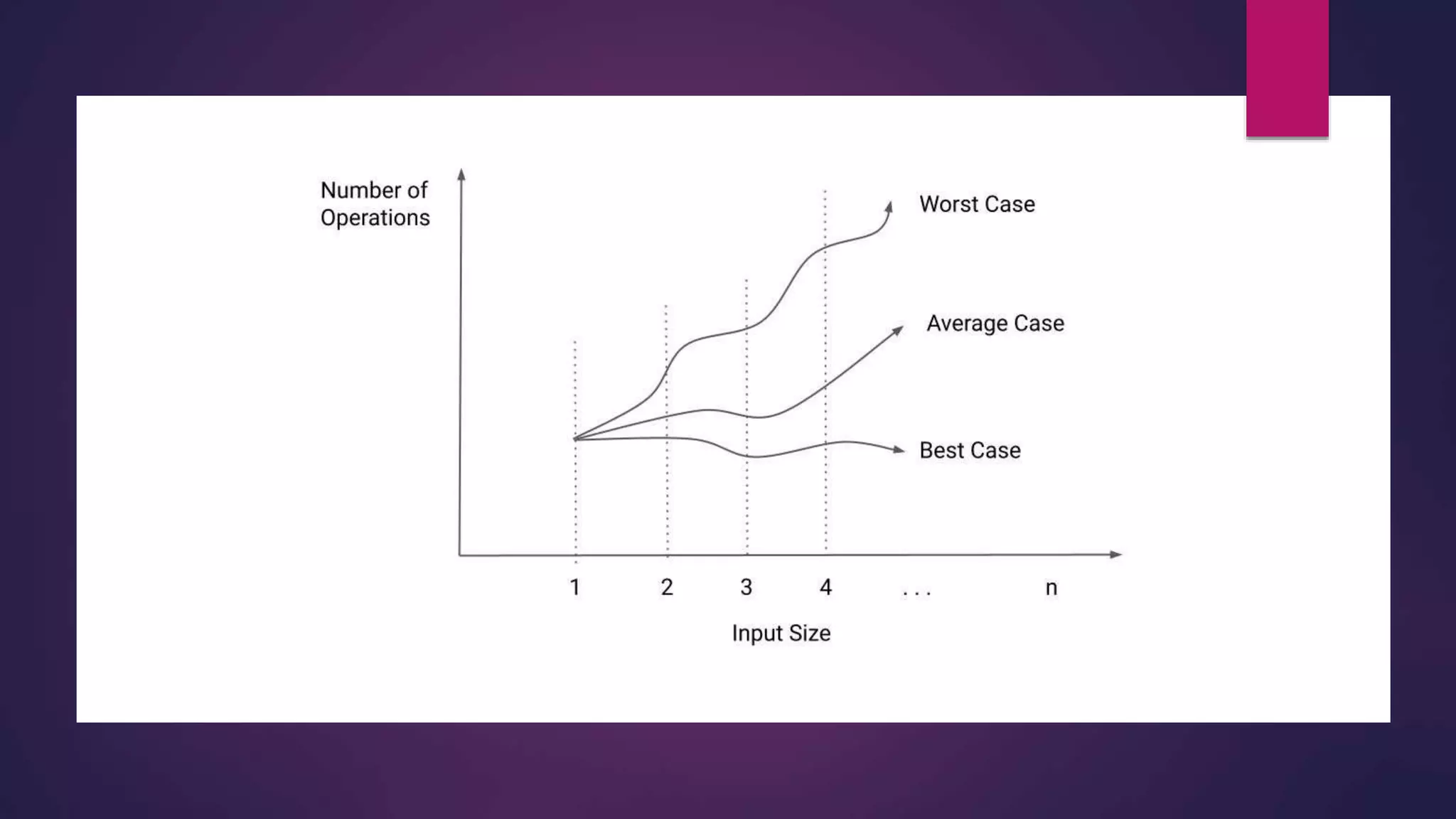
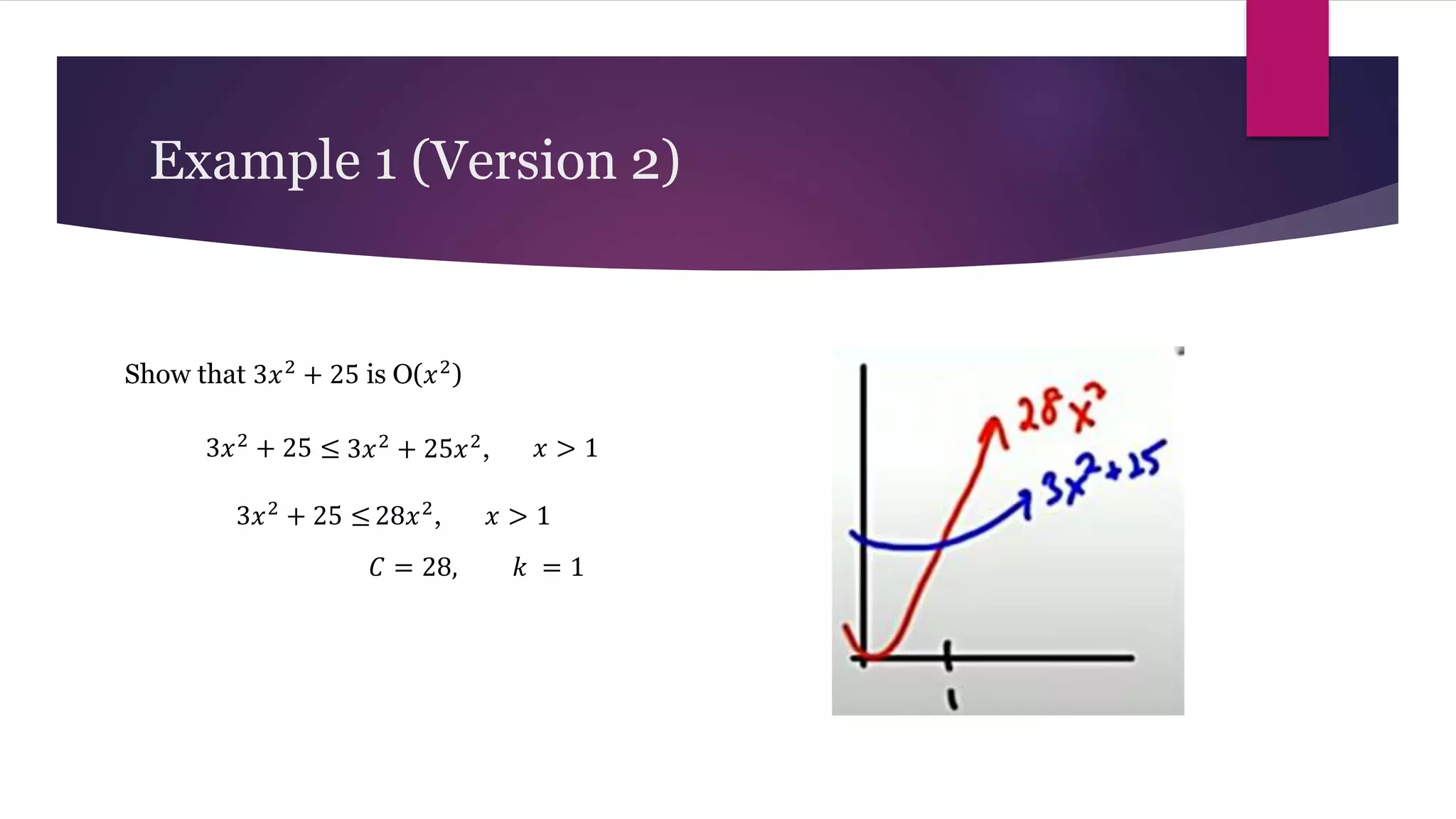
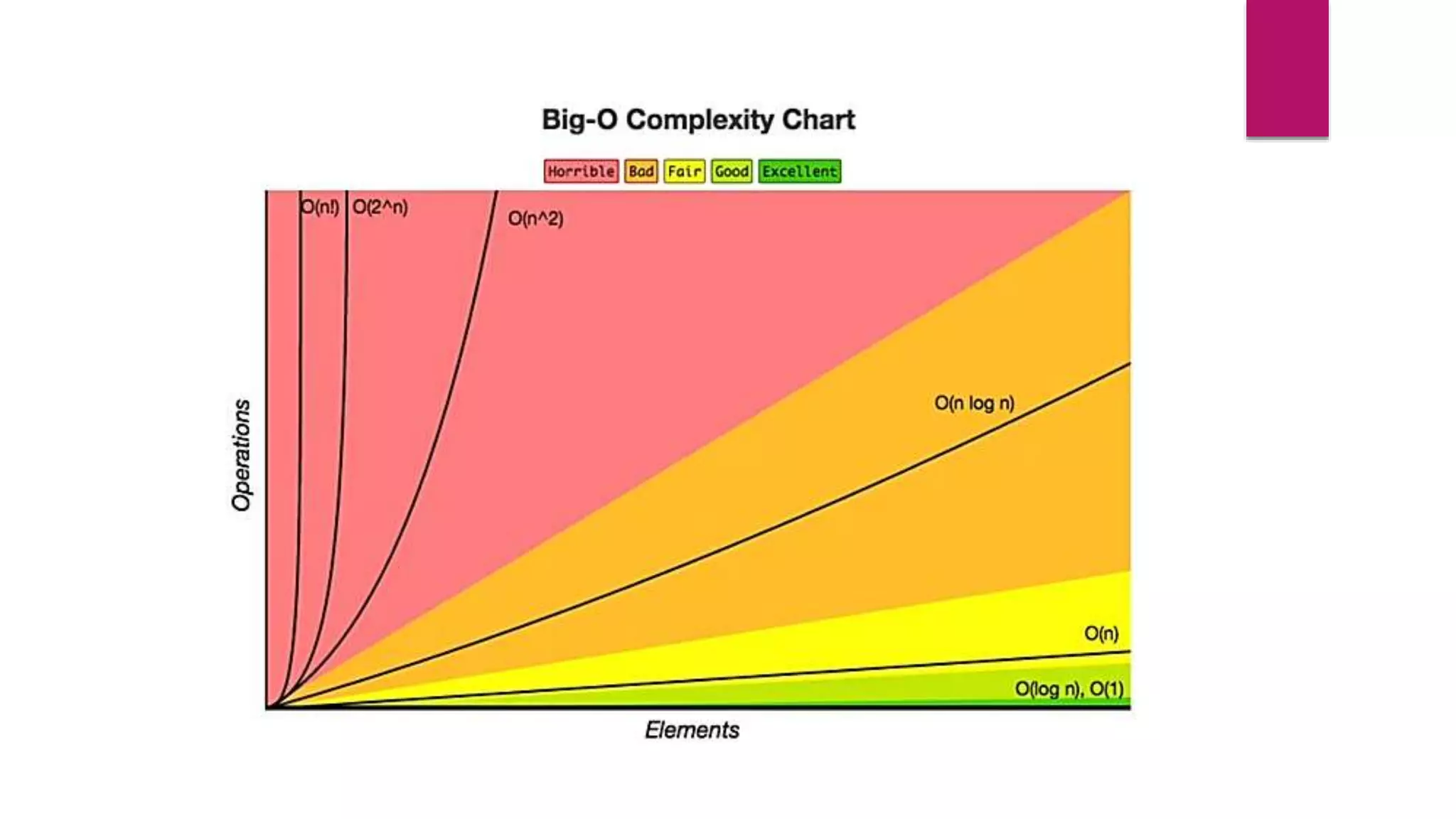
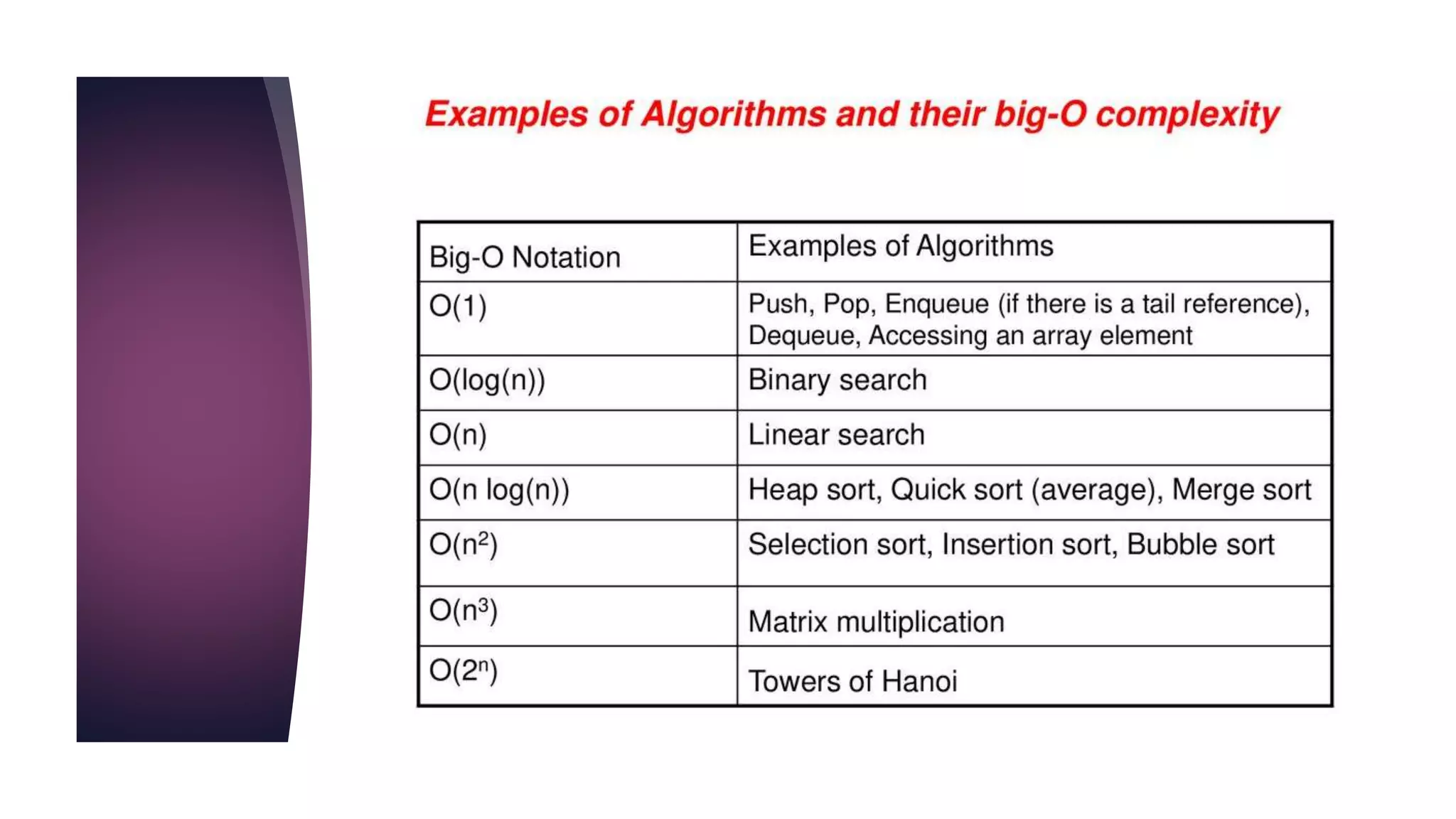
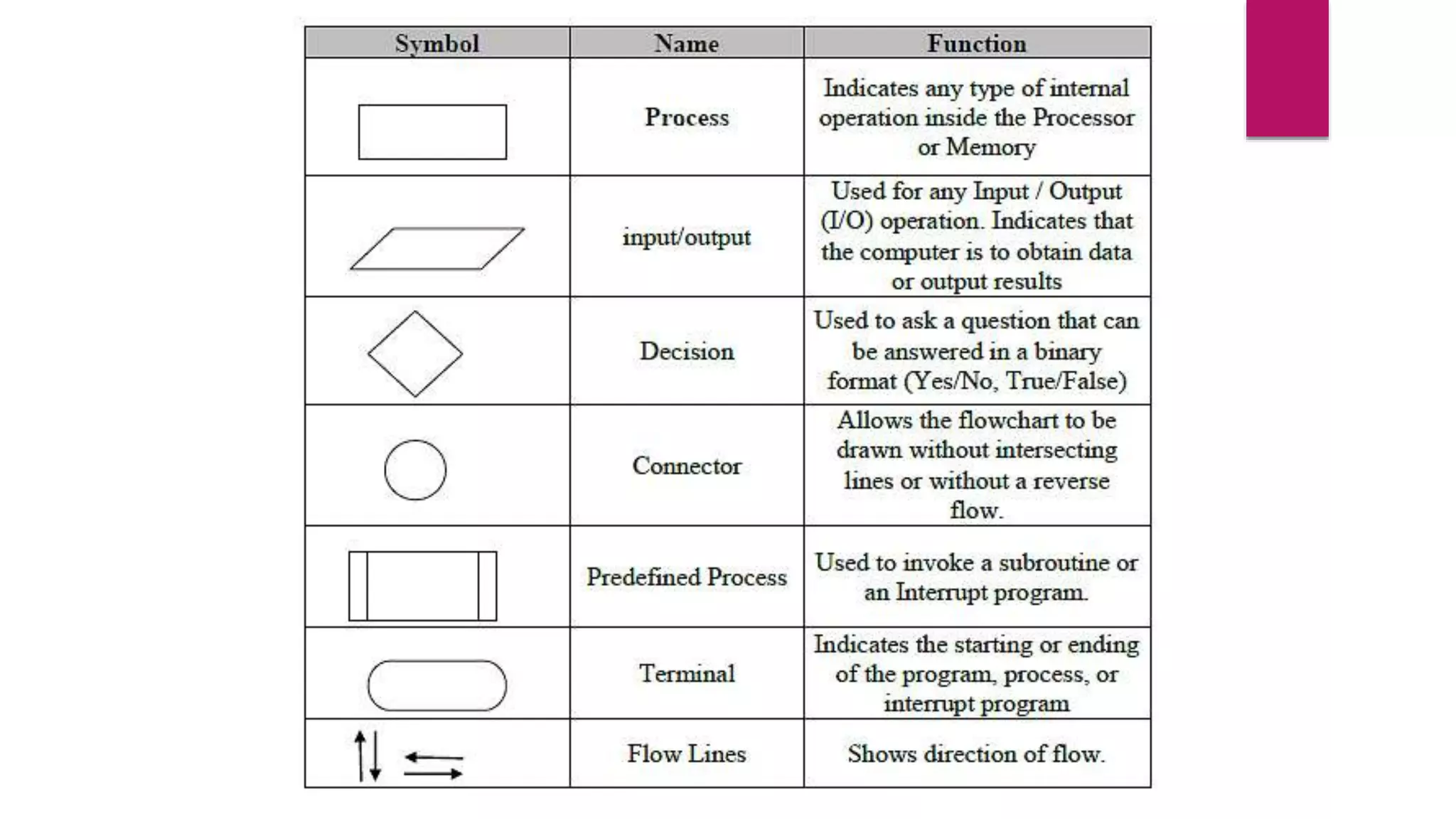
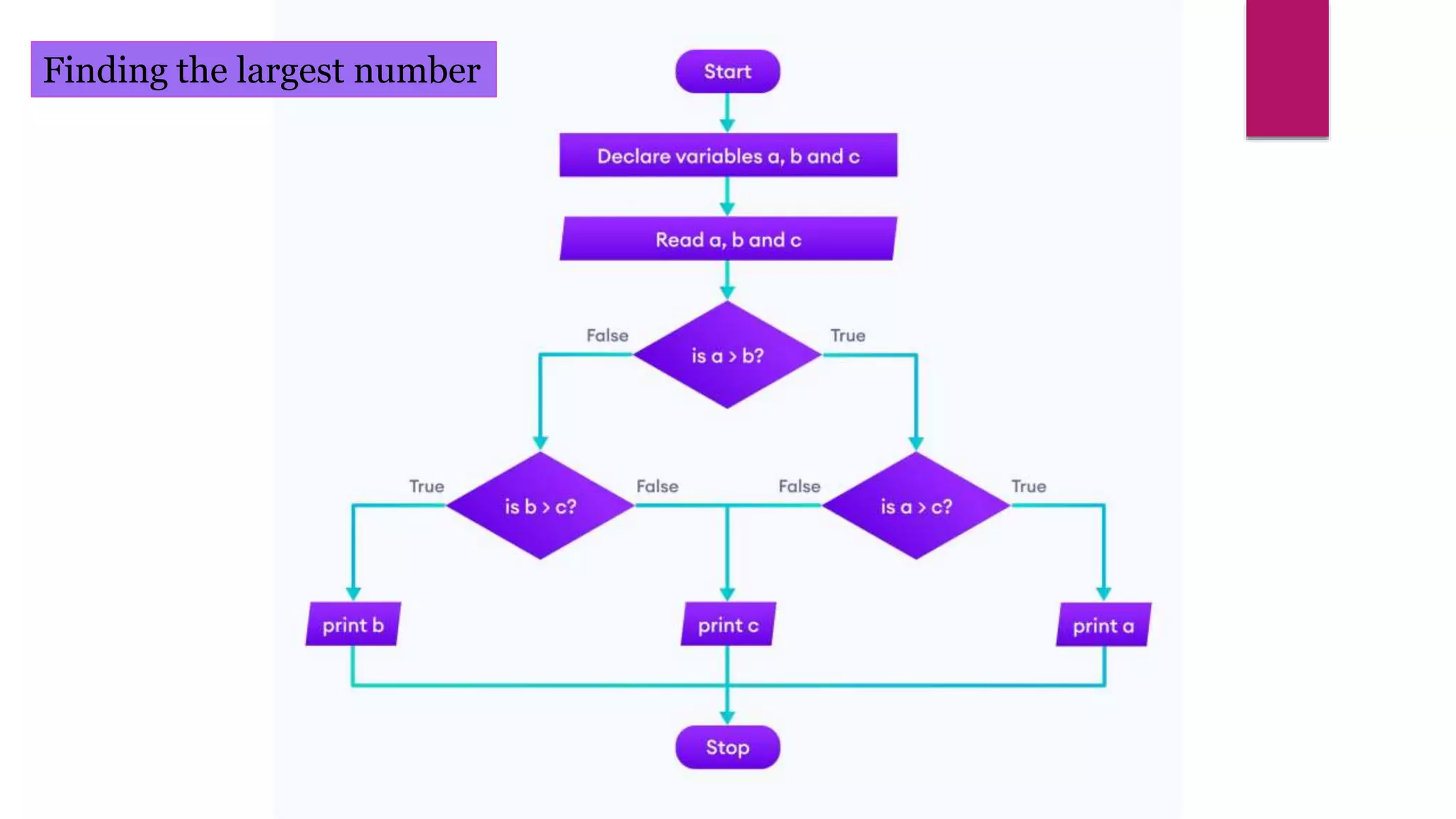
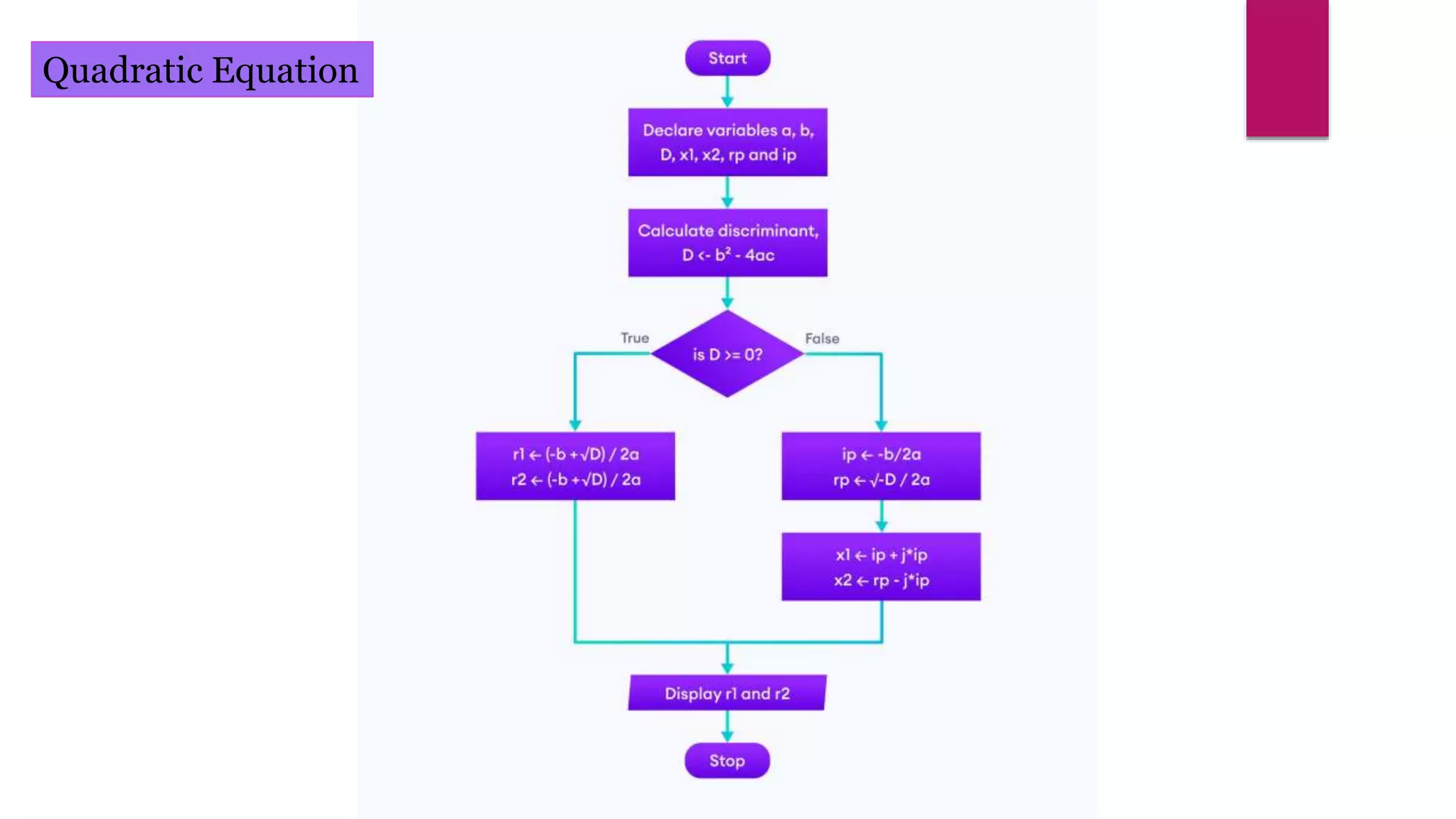
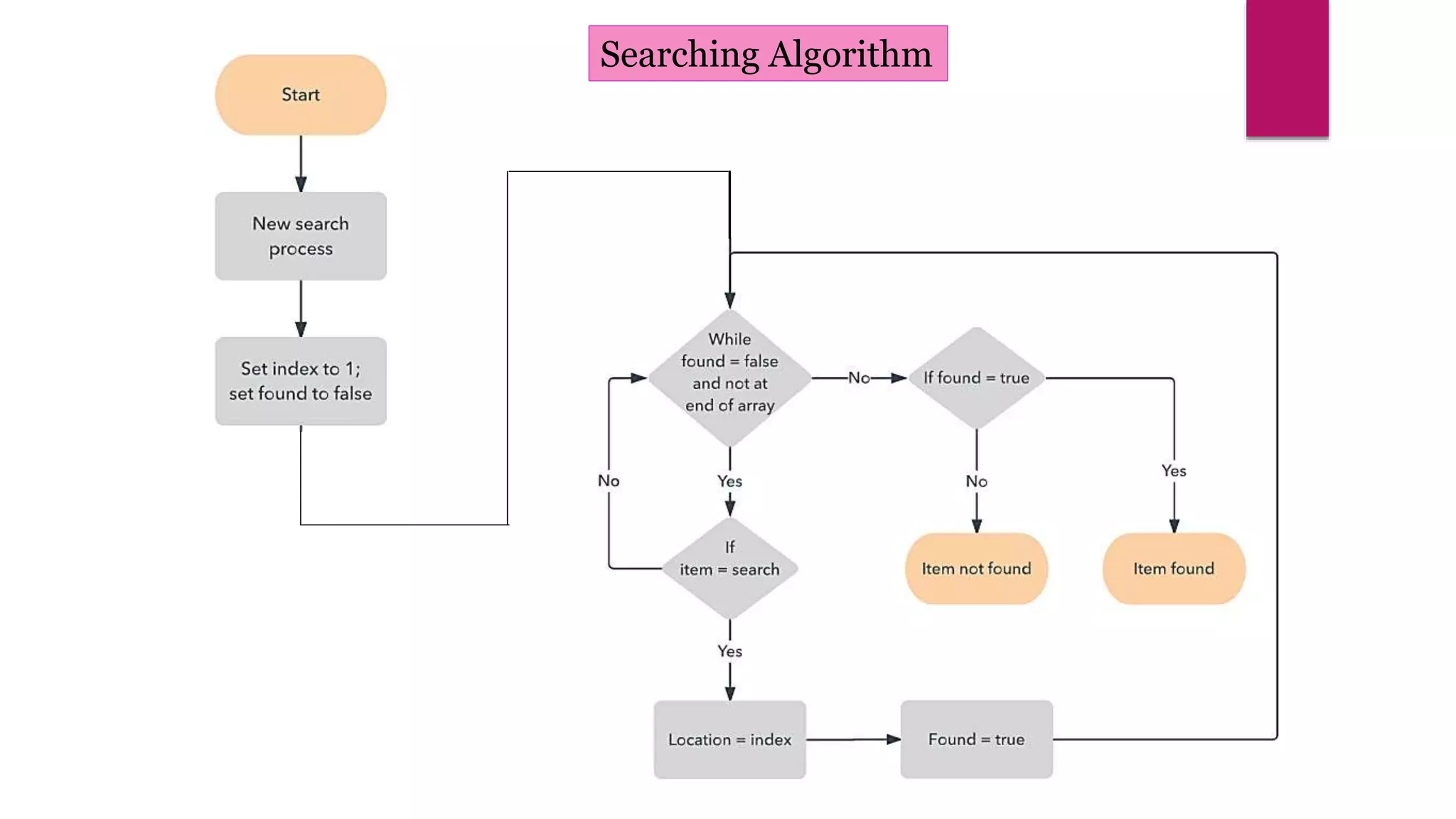
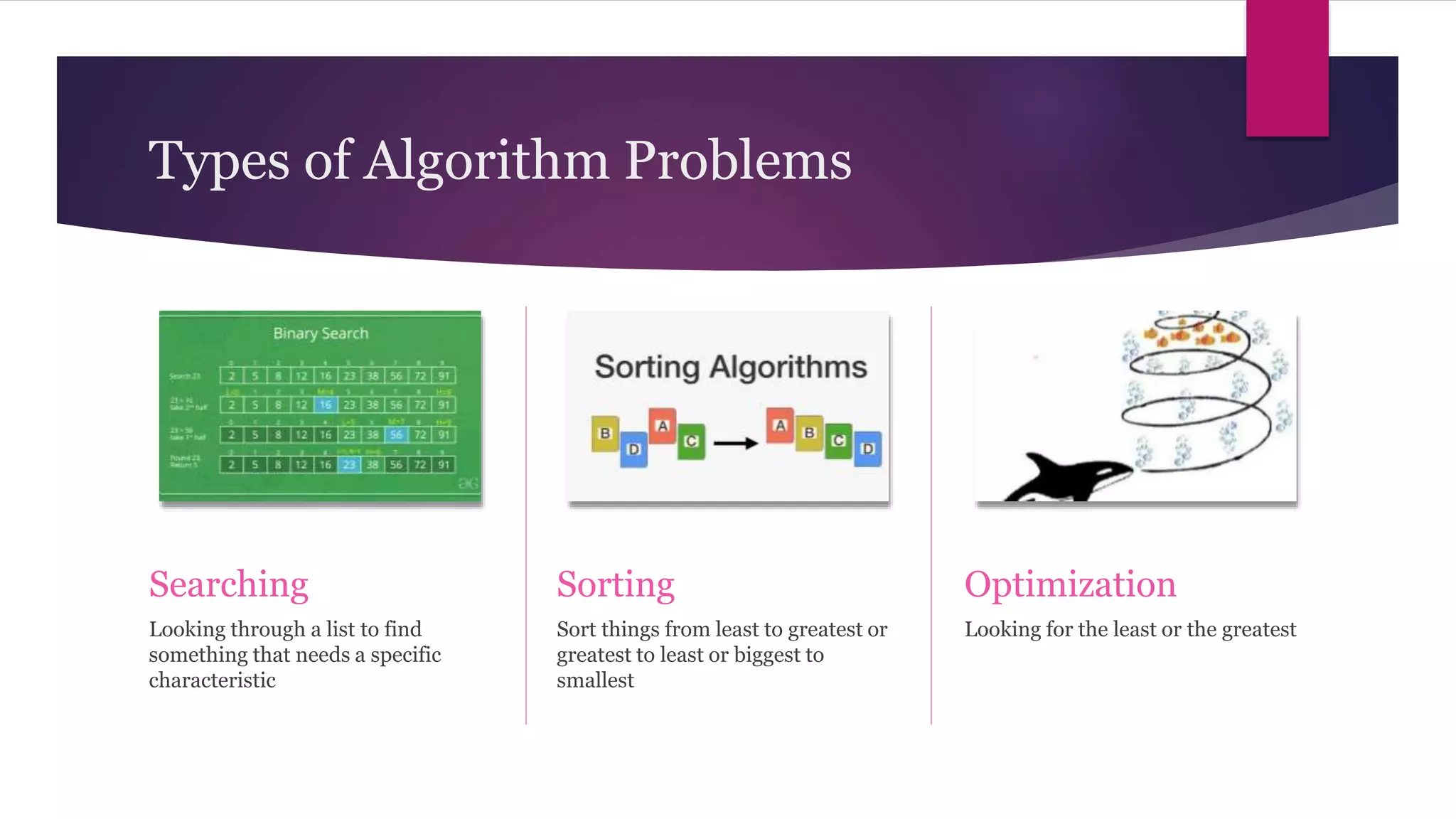
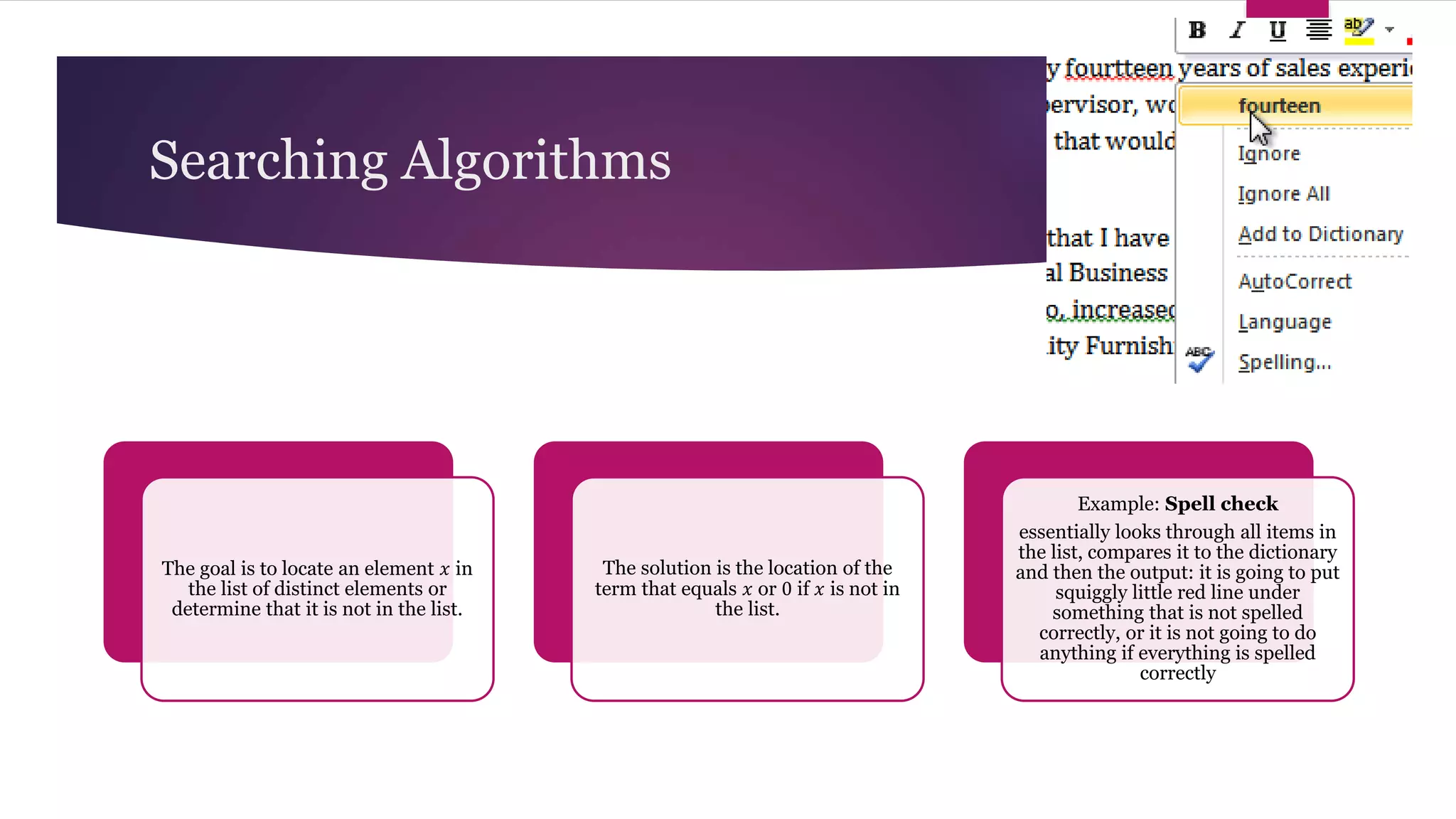
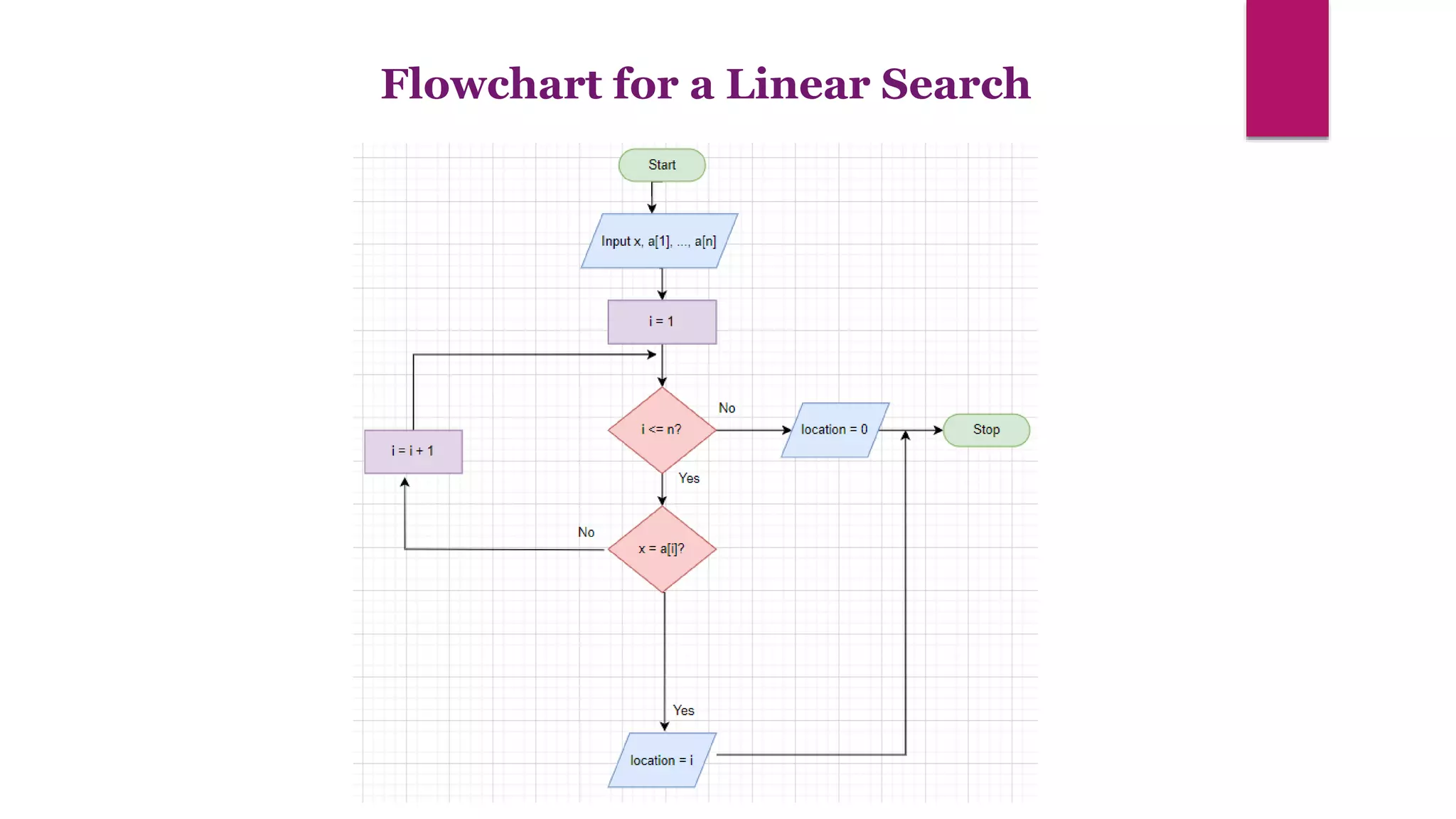
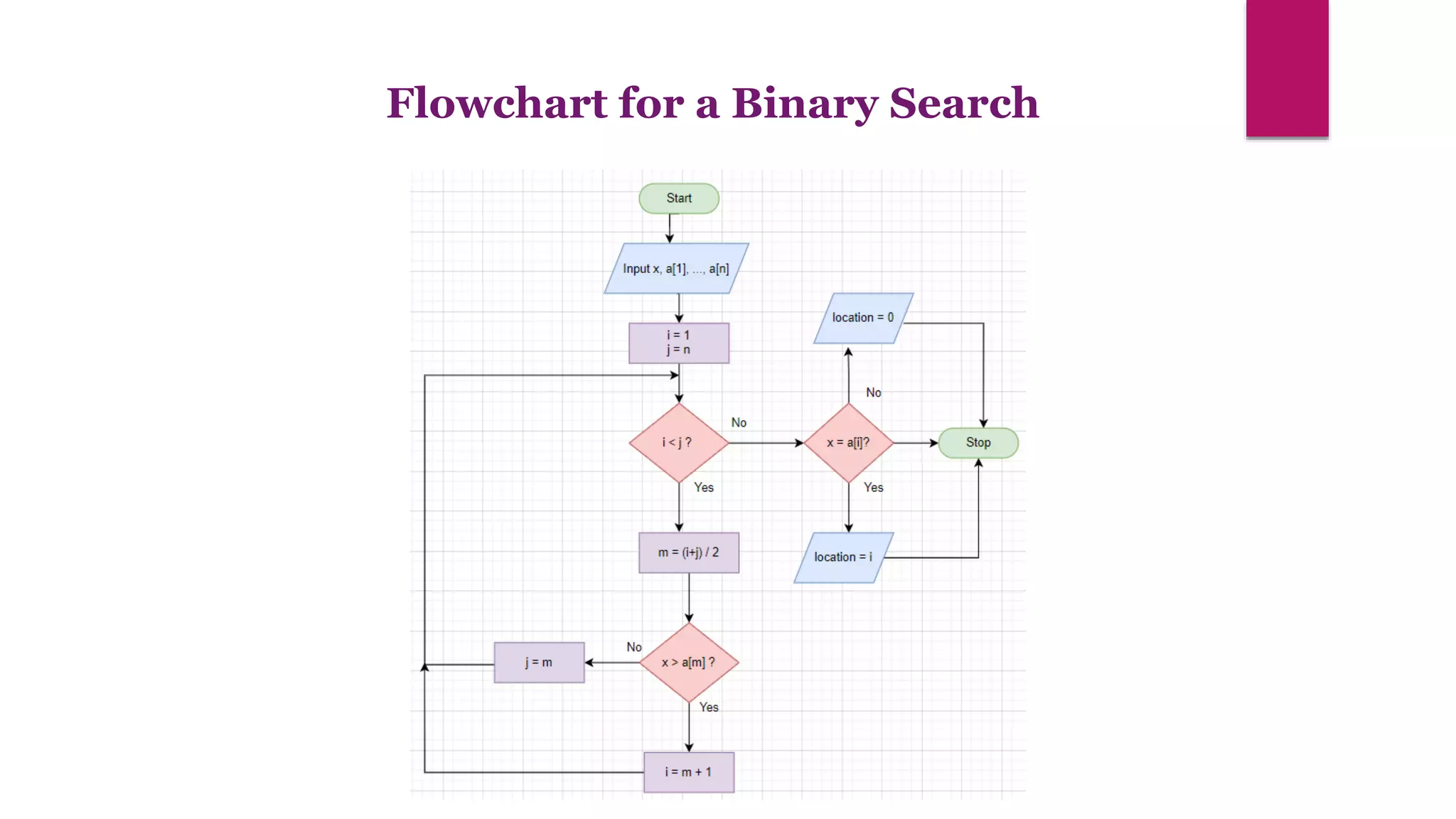
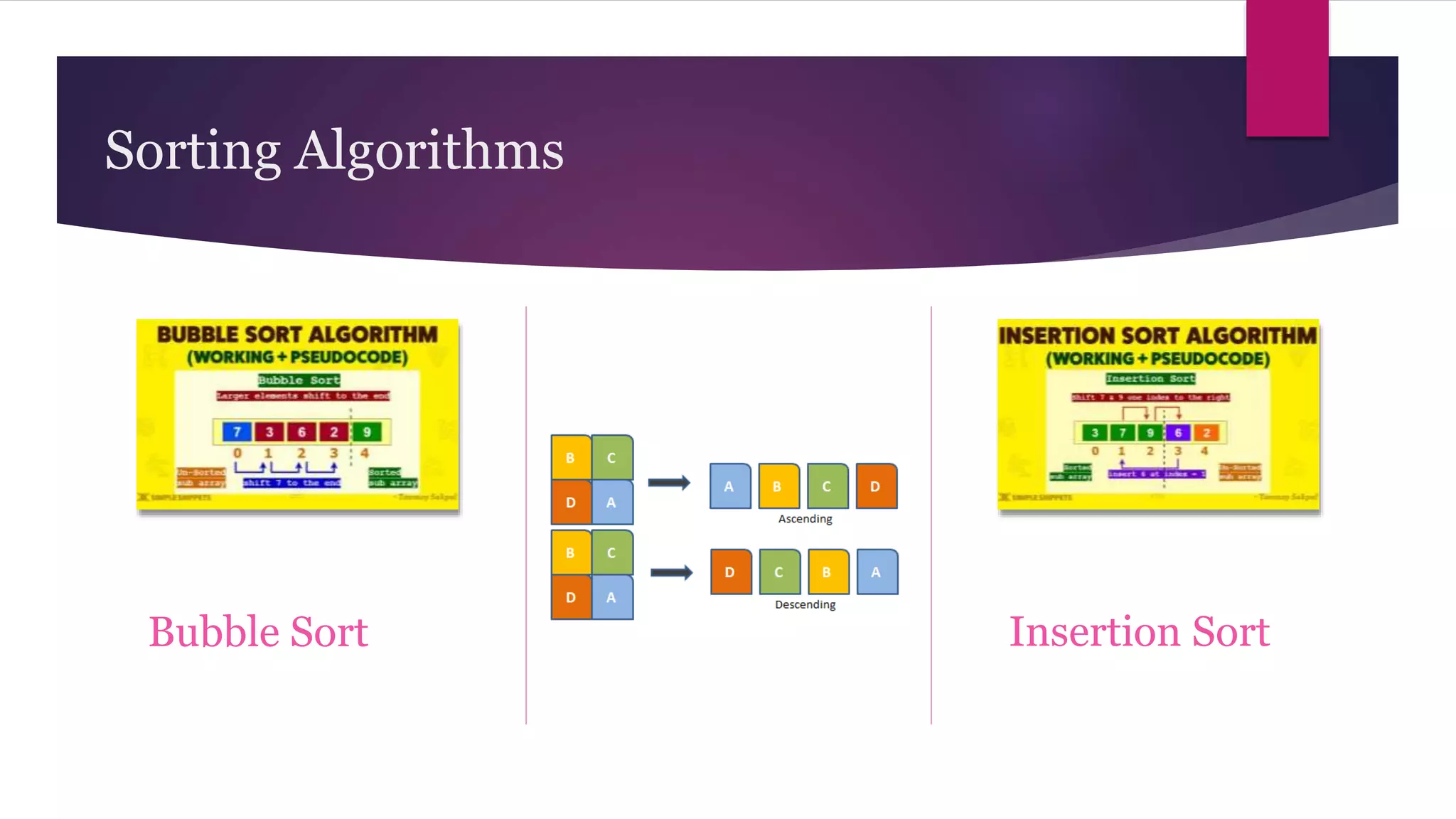
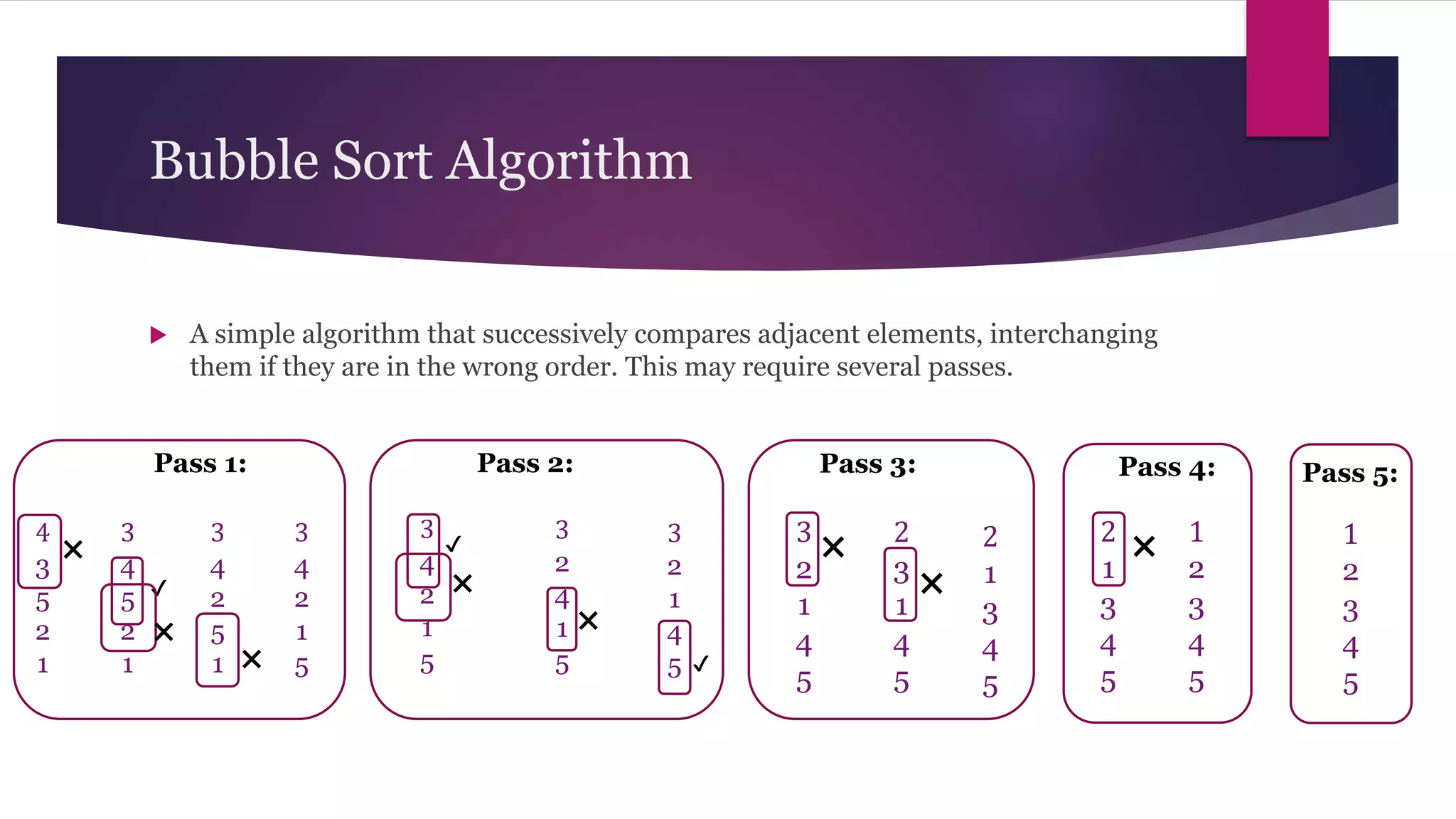
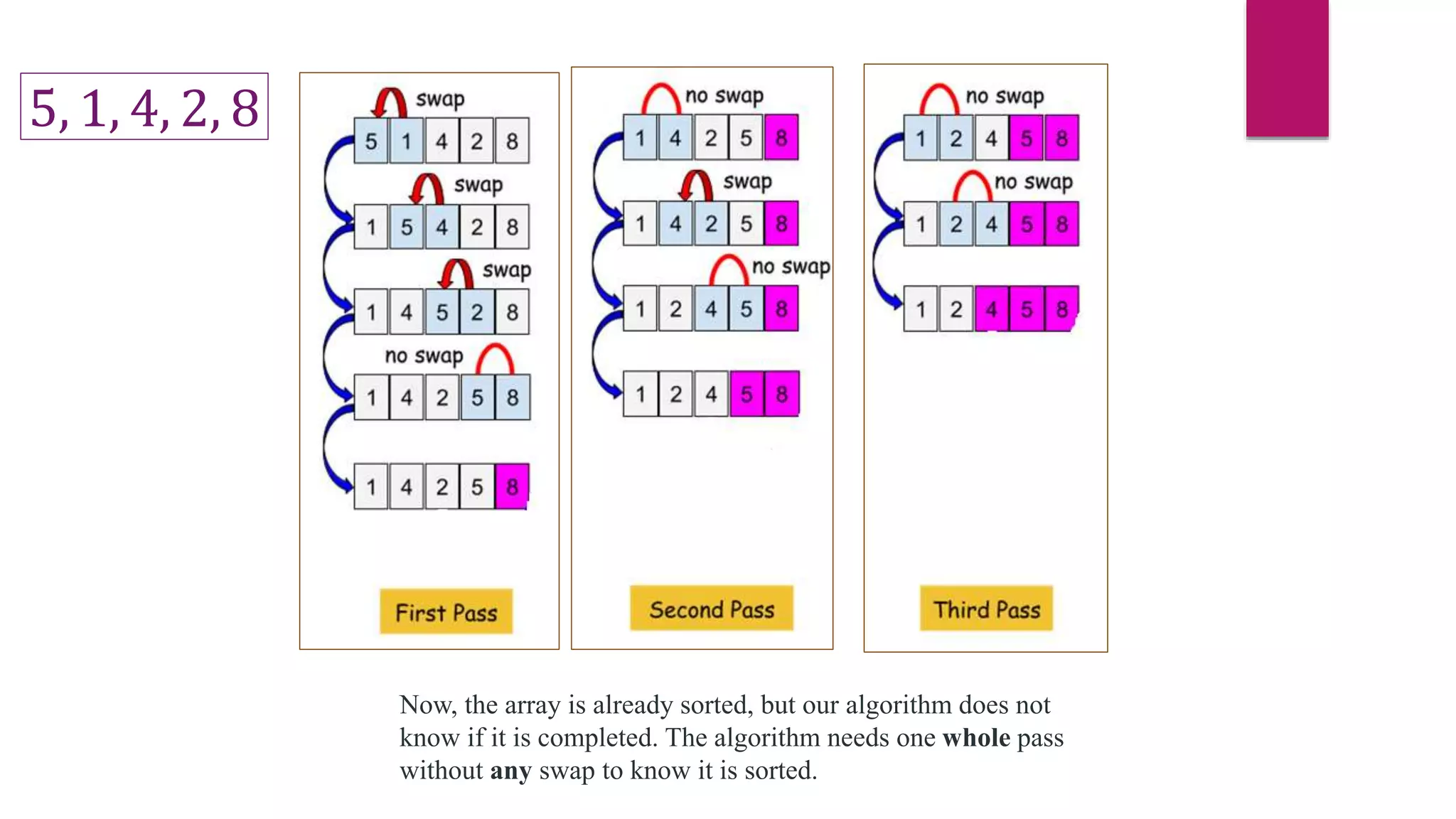
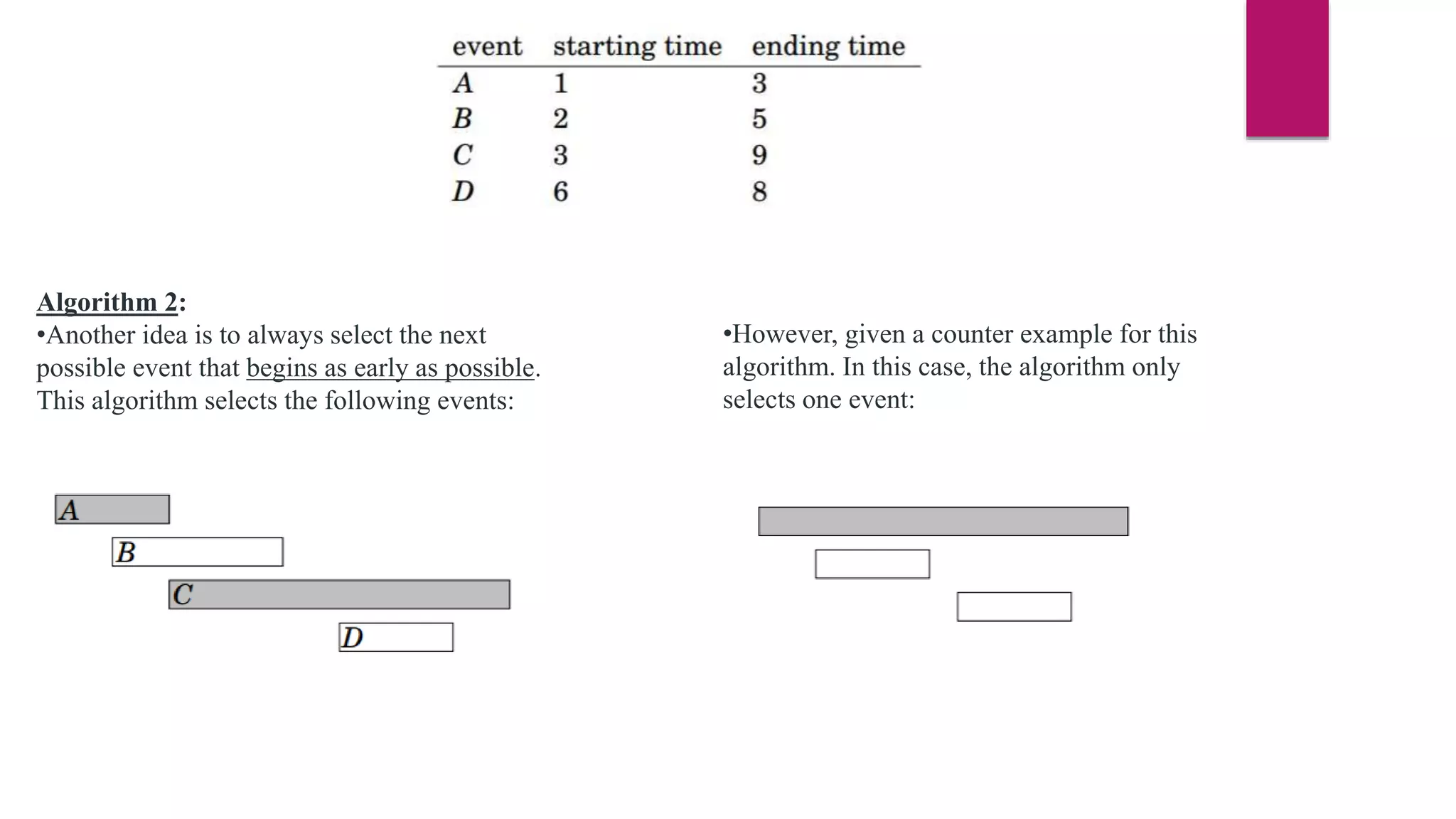
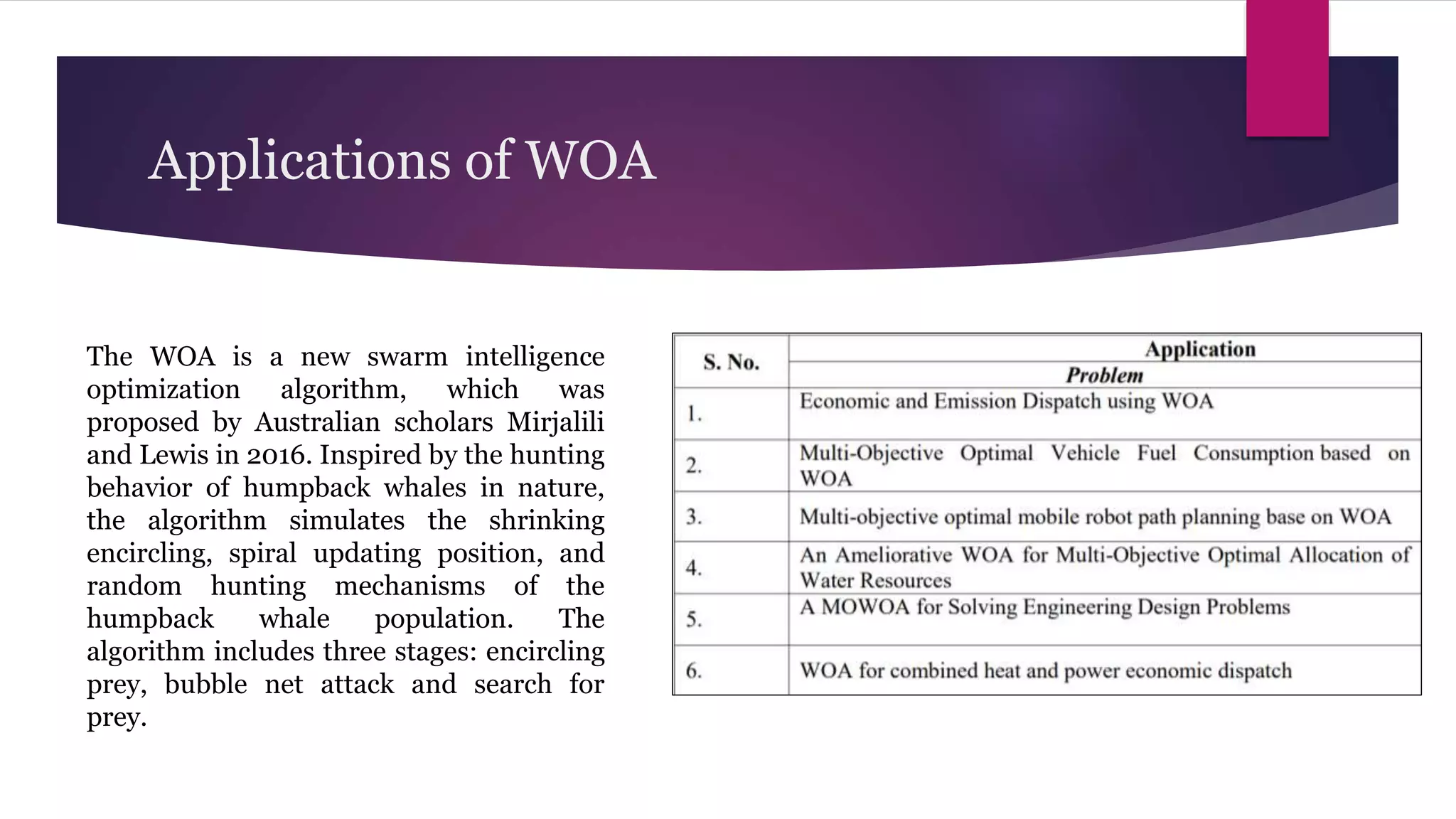
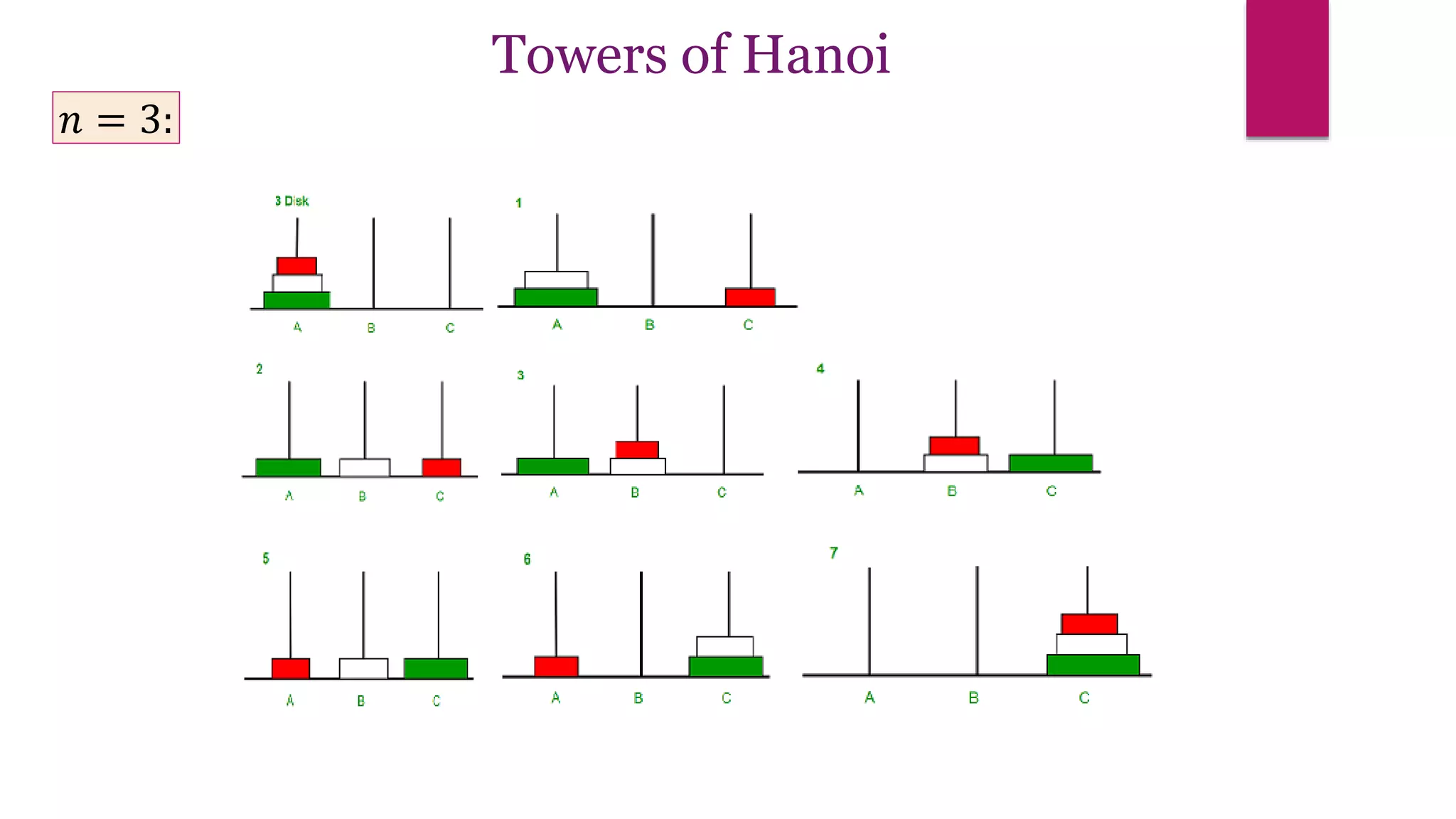
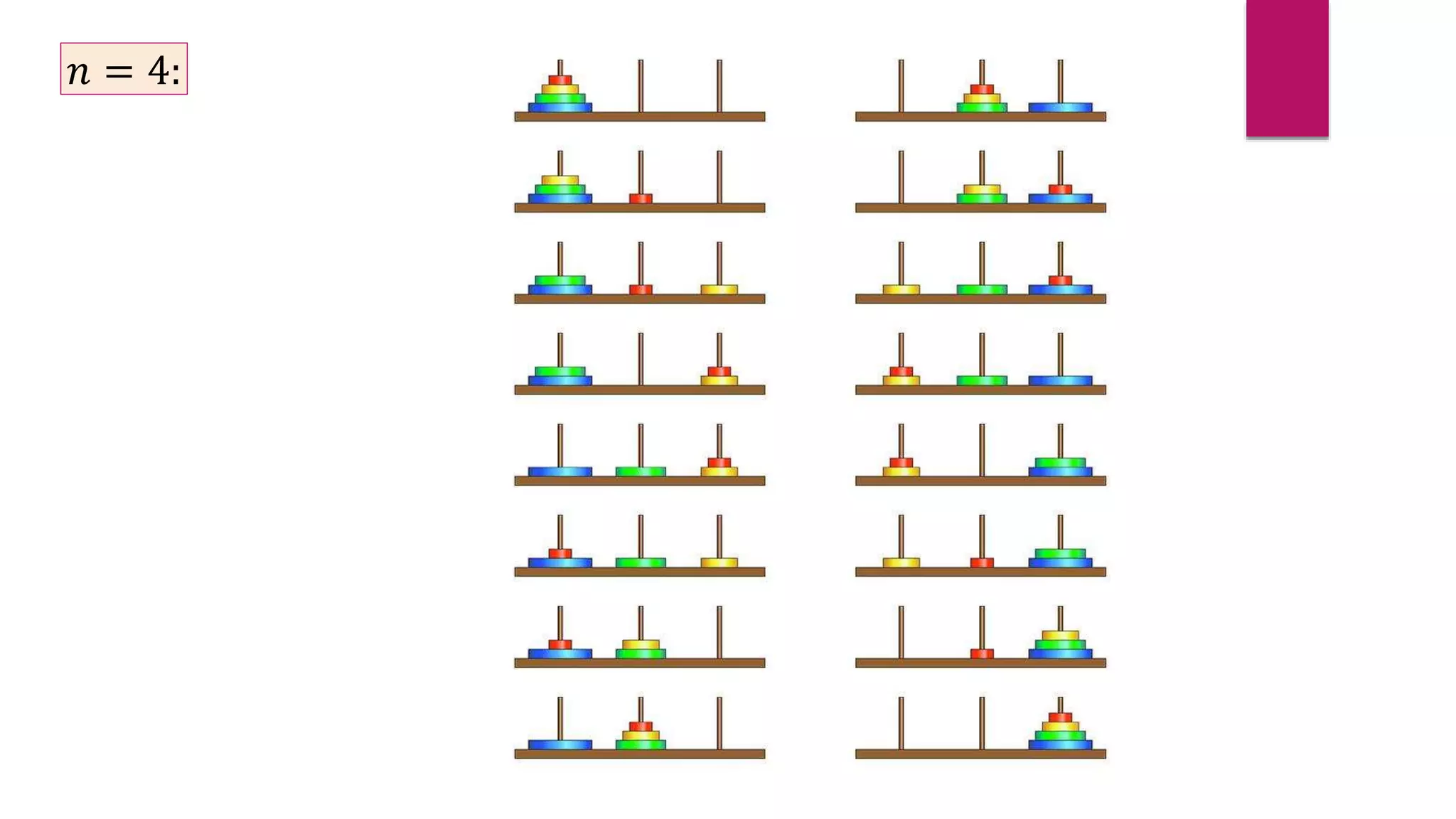
The document provides an overview of algorithms and pseudocode. It discusses key algorithm concepts like searching, sorting, and optimization problems. Specific searching algorithms covered are linear search and binary search, while sorting algorithms discussed include bubble sort and insertion sort. Pseudocode is introduced as a way to describe algorithms using plain language instead of a programming syntax. Examples are provided to demonstrate linear search, binary search, and bubble sort algorithms. The document aims to teach the fundamentals of algorithms through examples and explanations of common algorithm problems and solutions.






![Input: 𝑎𝑟𝑟[ ] = {10, 324, 45, 90,9808}; 𝑂𝑢𝑡𝑝𝑢𝑡: 9808
Input : 𝑎𝑟𝑟[ ] = {20, 10, 100, 20, 4}; 𝑂𝑢𝑡𝑝𝑢𝑡 ∶ 100
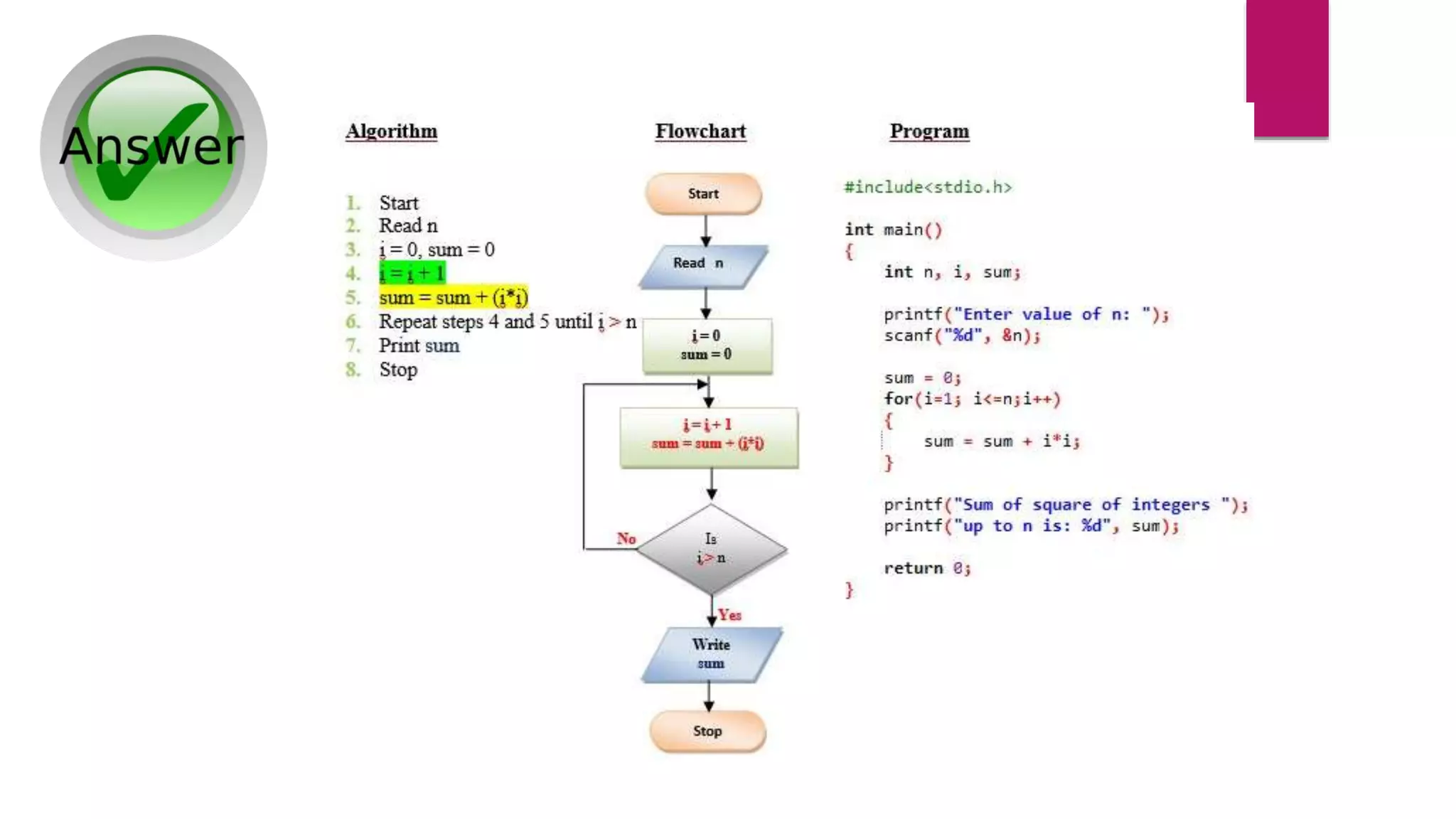
Go through each step of the given algorithm to find the max value in
array (show every step).](https://image.slidesharecdn.com/lecture-1-algorithms-230214193740-2d2c09f6/75/Lecture-1-Algorithms-pptx-13-2048.jpg)



















































![// Fibonacci Series using Recursion
#include <iostream>
using namespace std;
int fib(int n)
{
if (n <= 1)
return n;
return fib(n - 1) + fib(n - 2);
}
int main()
{
int n = 9;
cout << fib(n);
return 0;
}
#include<iostream>
using namespace std;
class GFG{
public:
int fib(int n)
{
int f[n + 2];
int i;
f[0] = 0;
f[1] = 1;
for(i = 2; i <= n; i++)
{
f[i] = f[i - 1] + f[i - 2];
}
return f[n];
}
};
int main ()
{
GFG g;
int n = 4;
cout << g.fib(n);
return 0;
}
// Fibonacci Series using Space Optimized Method
#include<bits/stdc++.h>
using namespace std;
int fib(int n)
{
int a = 0, b = 1, c, i;
if( n == 0)
return a;
for(i = 2; i <= n; i++)
{
c = a + b;
a = b;
b = c;
}
return b;
}
int main()
{
int n = 9;
cout << fib(n);
return 0;
}](https://image.slidesharecdn.com/lecture-1-algorithms-230214193740-2d2c09f6/75/Lecture-1-Algorithms-pptx-79-2048.jpg)