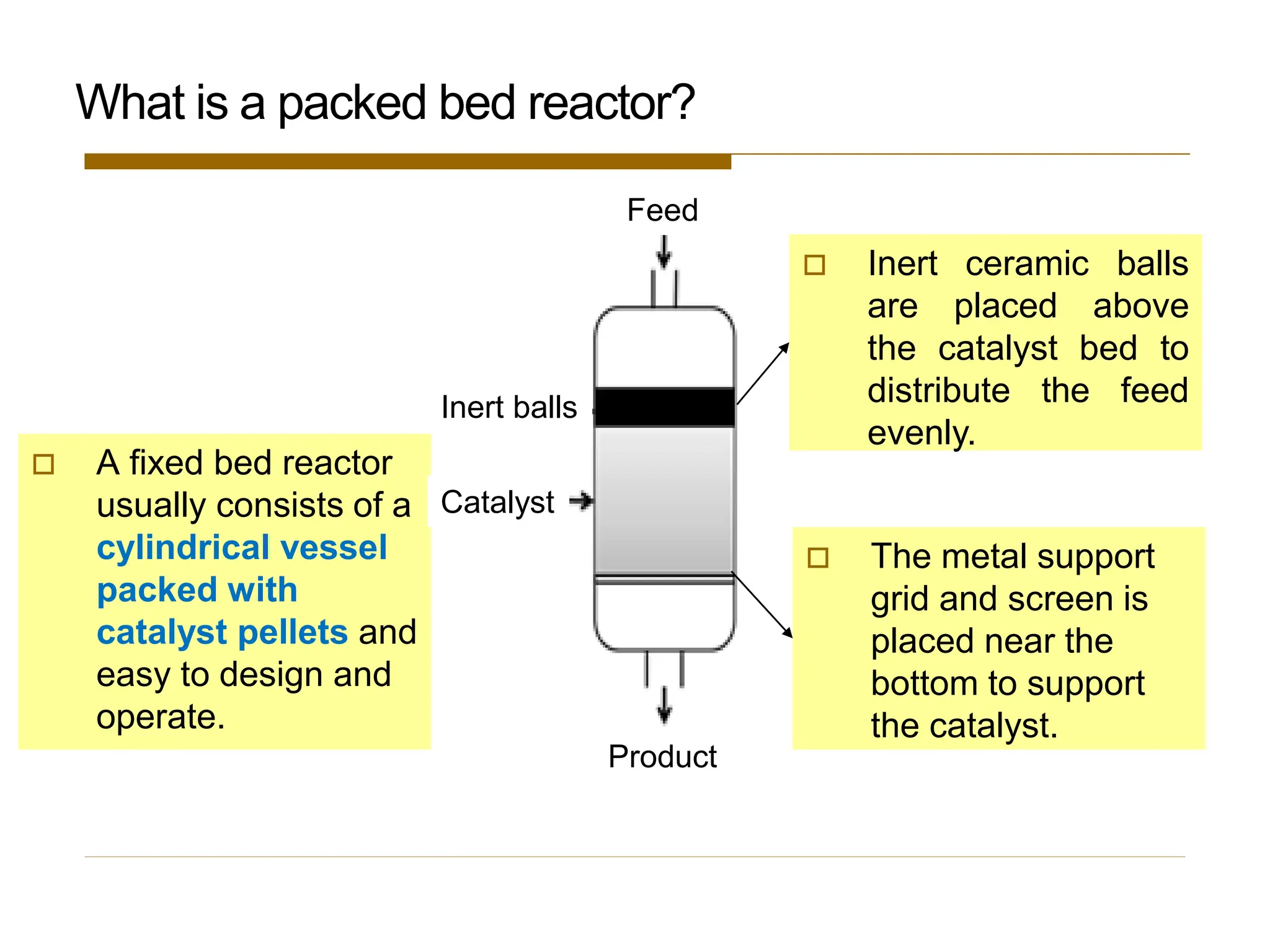
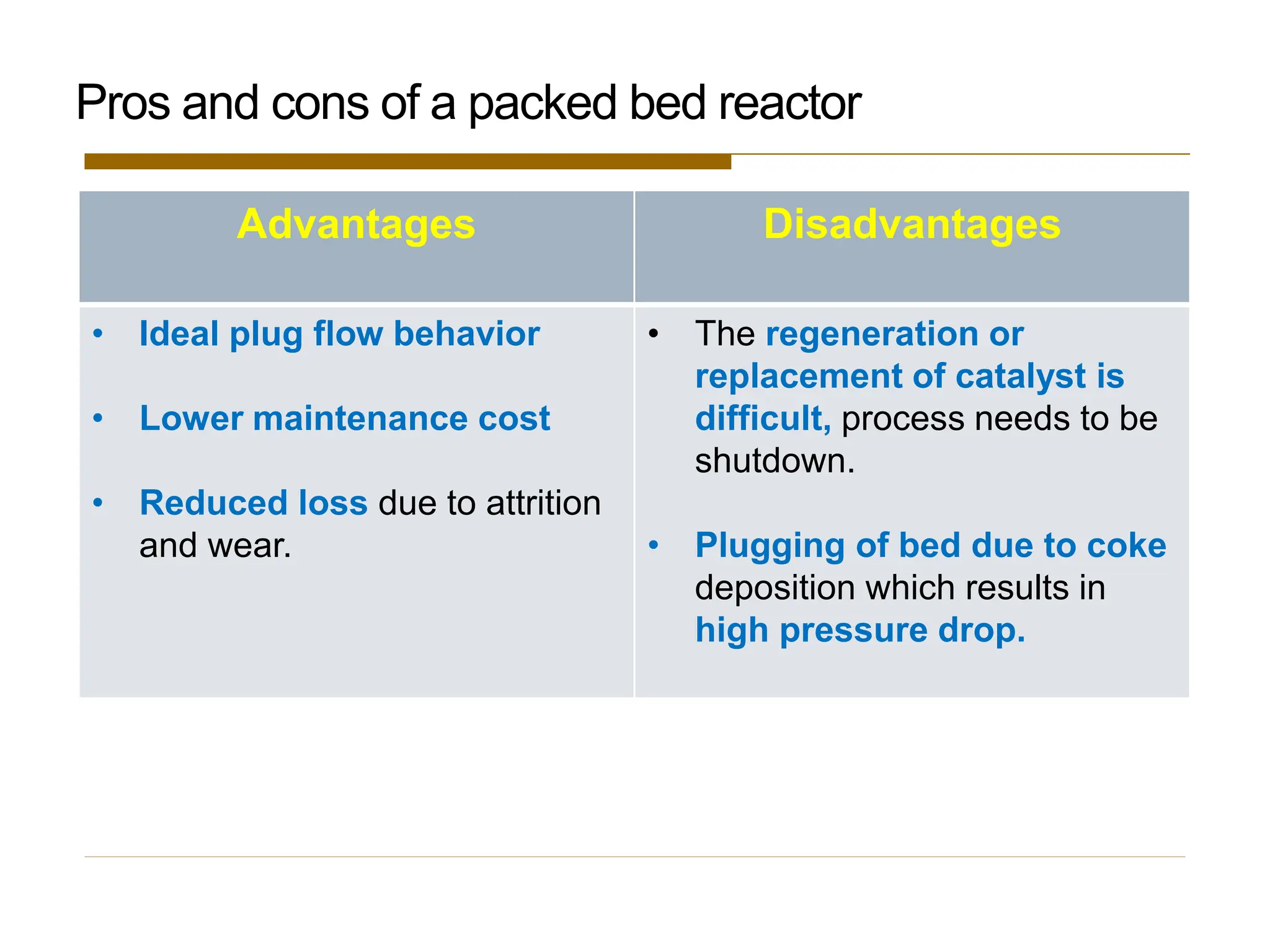
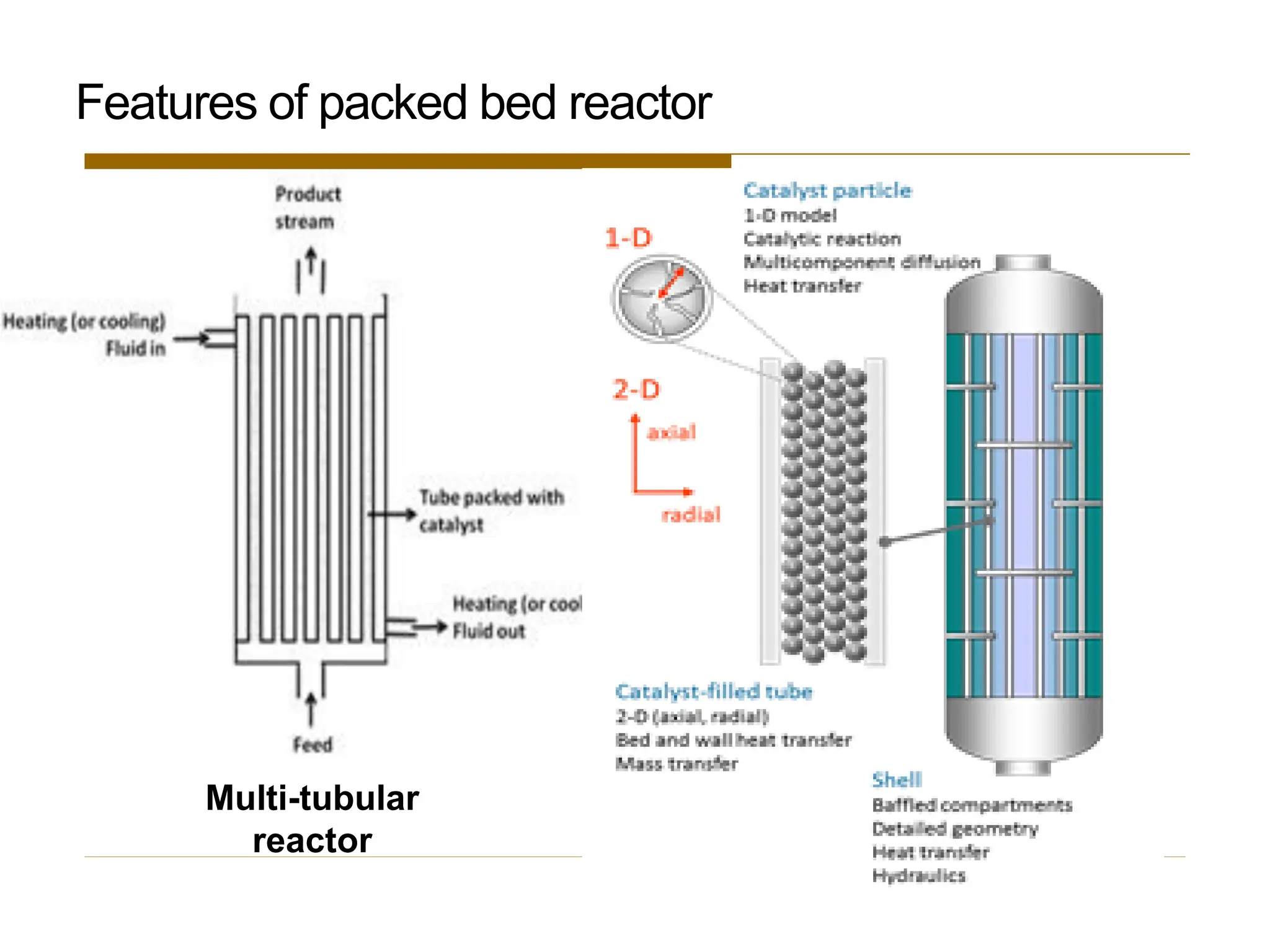
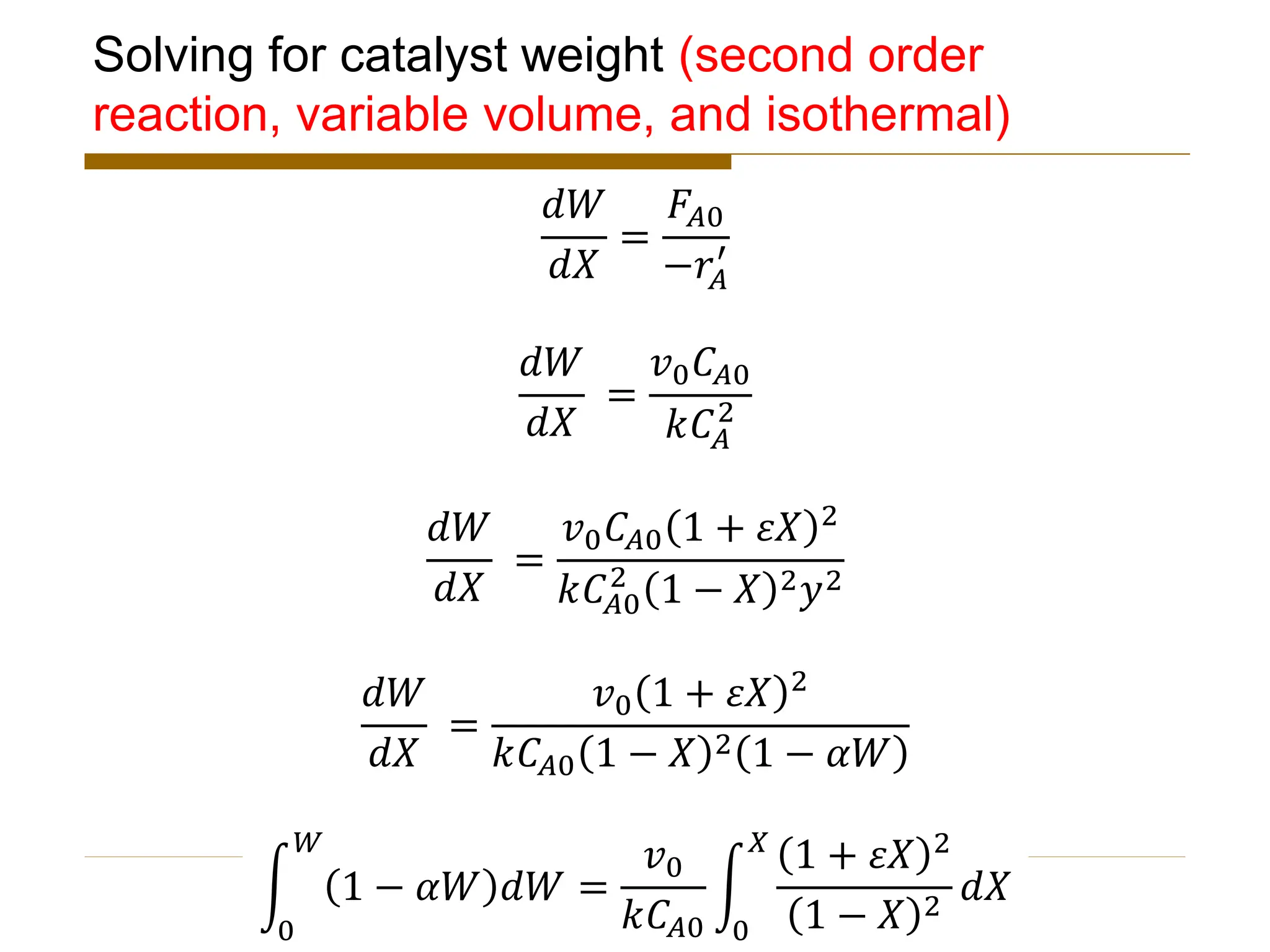
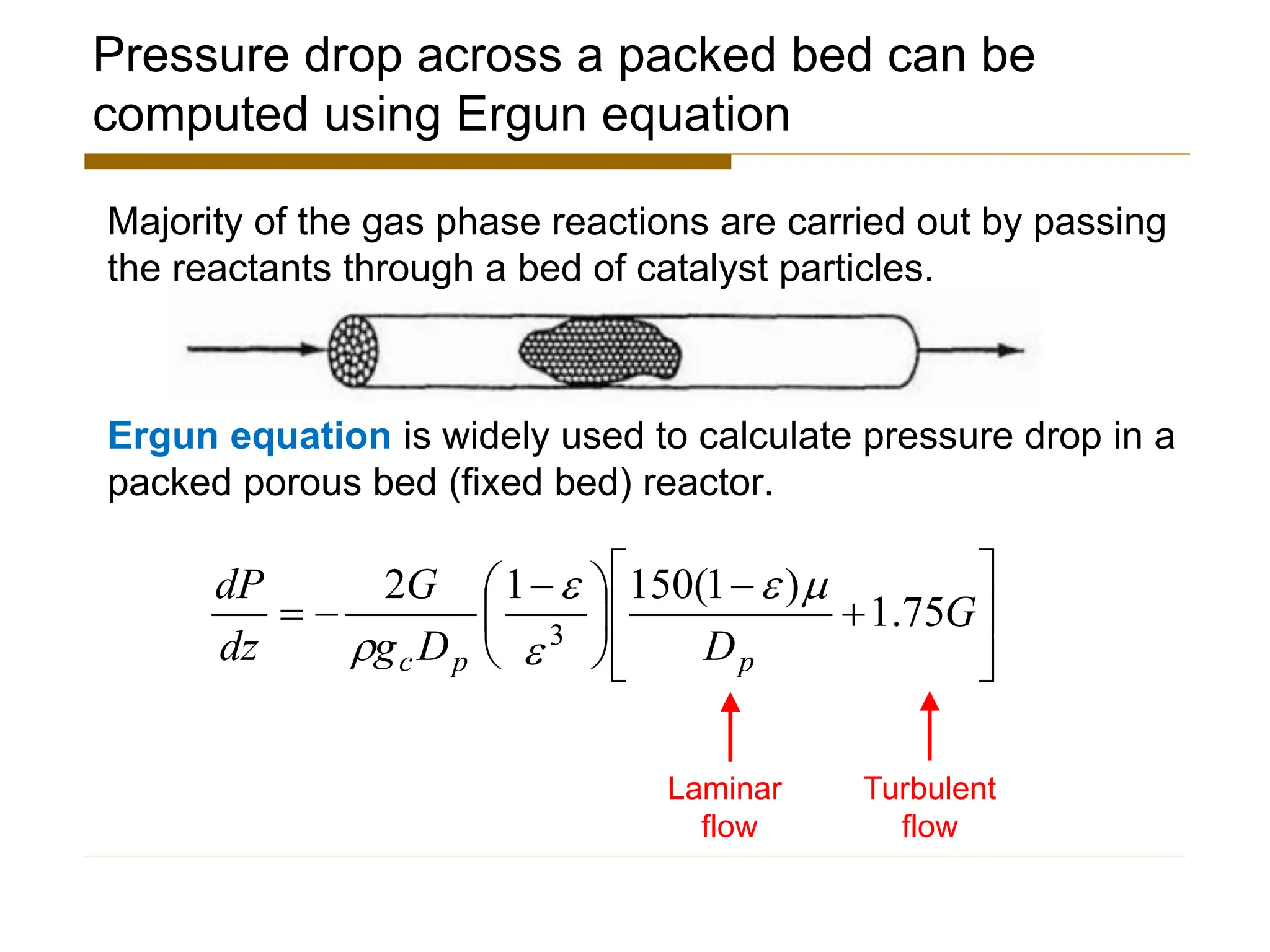
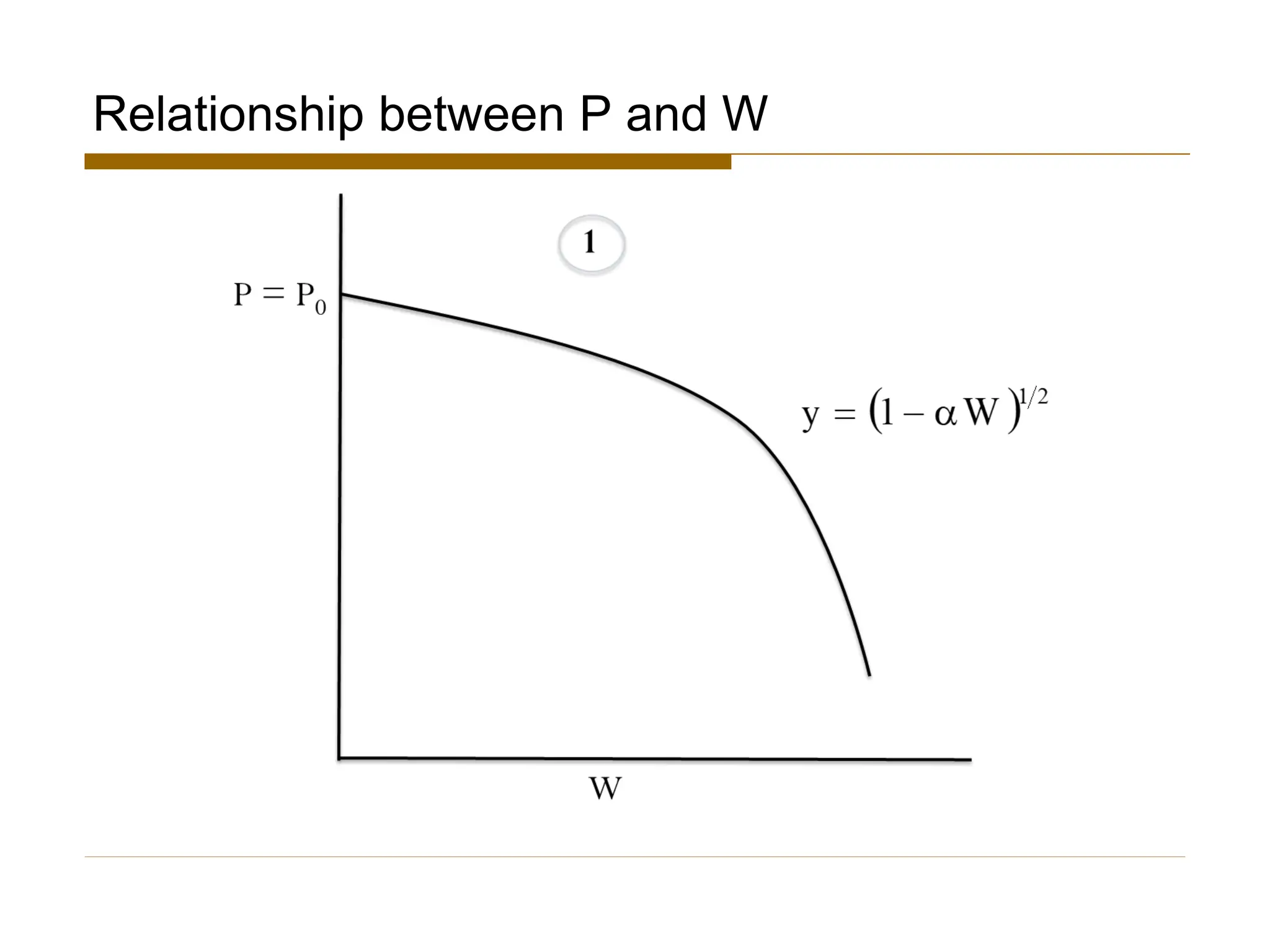
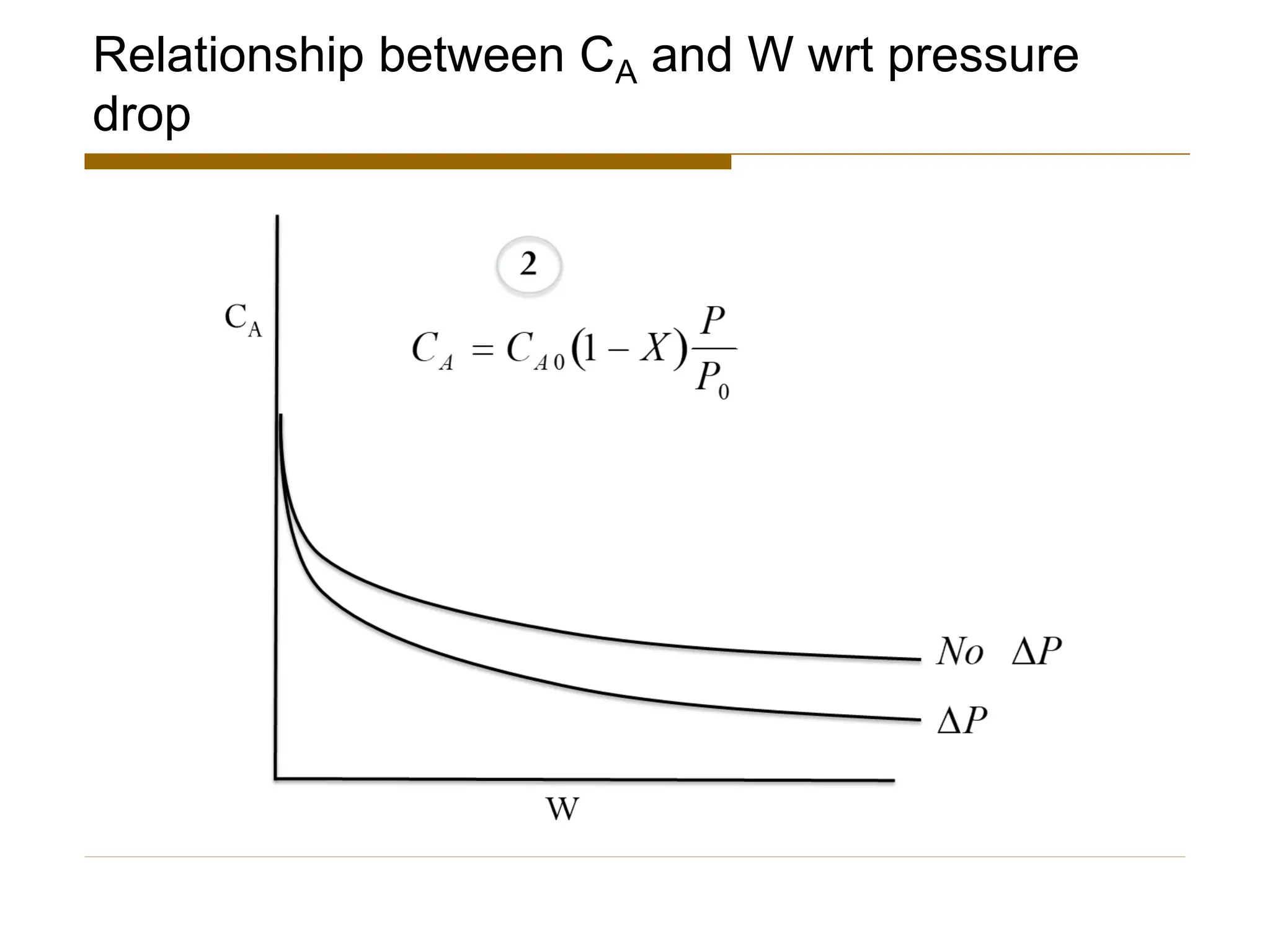
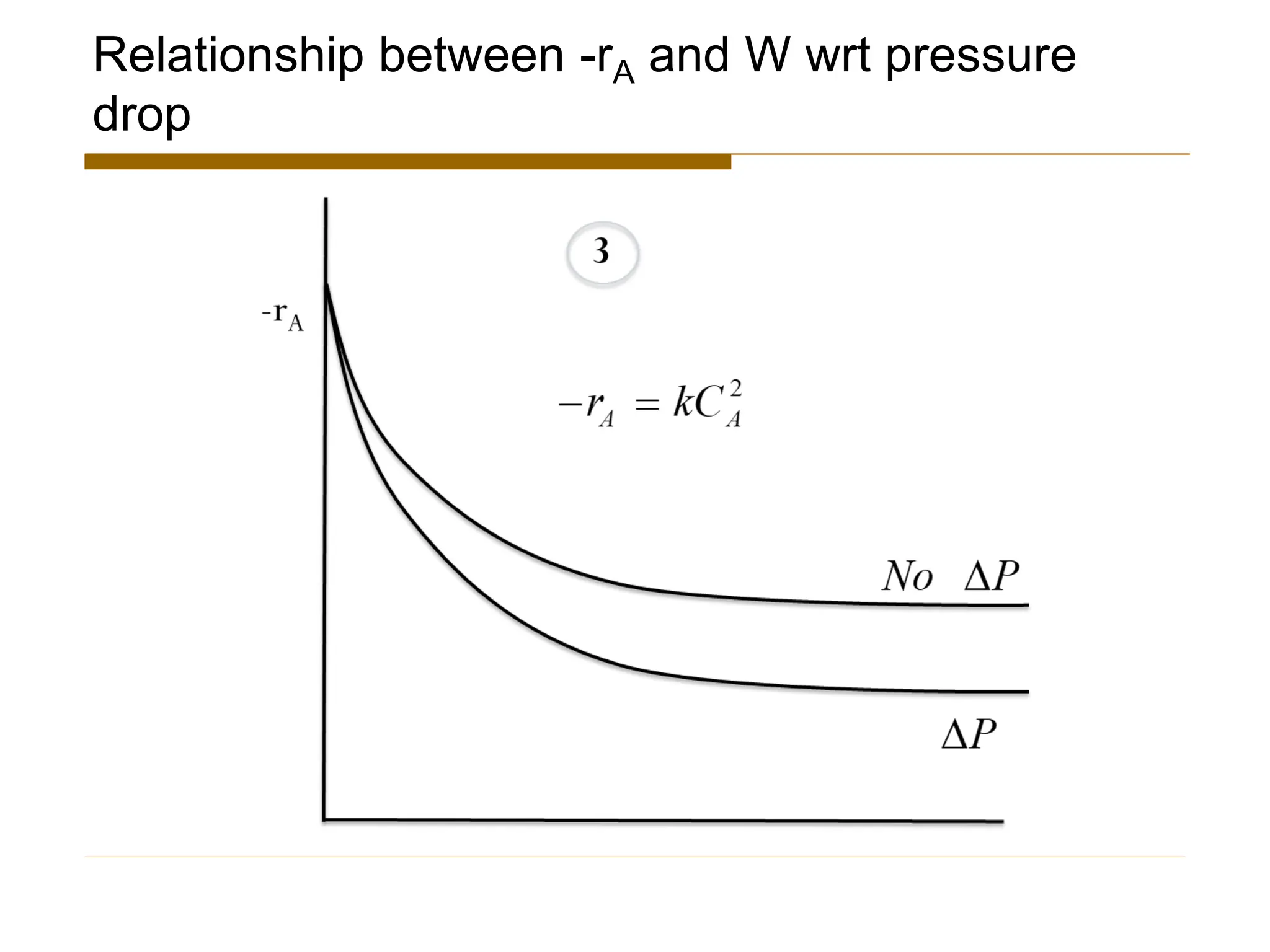
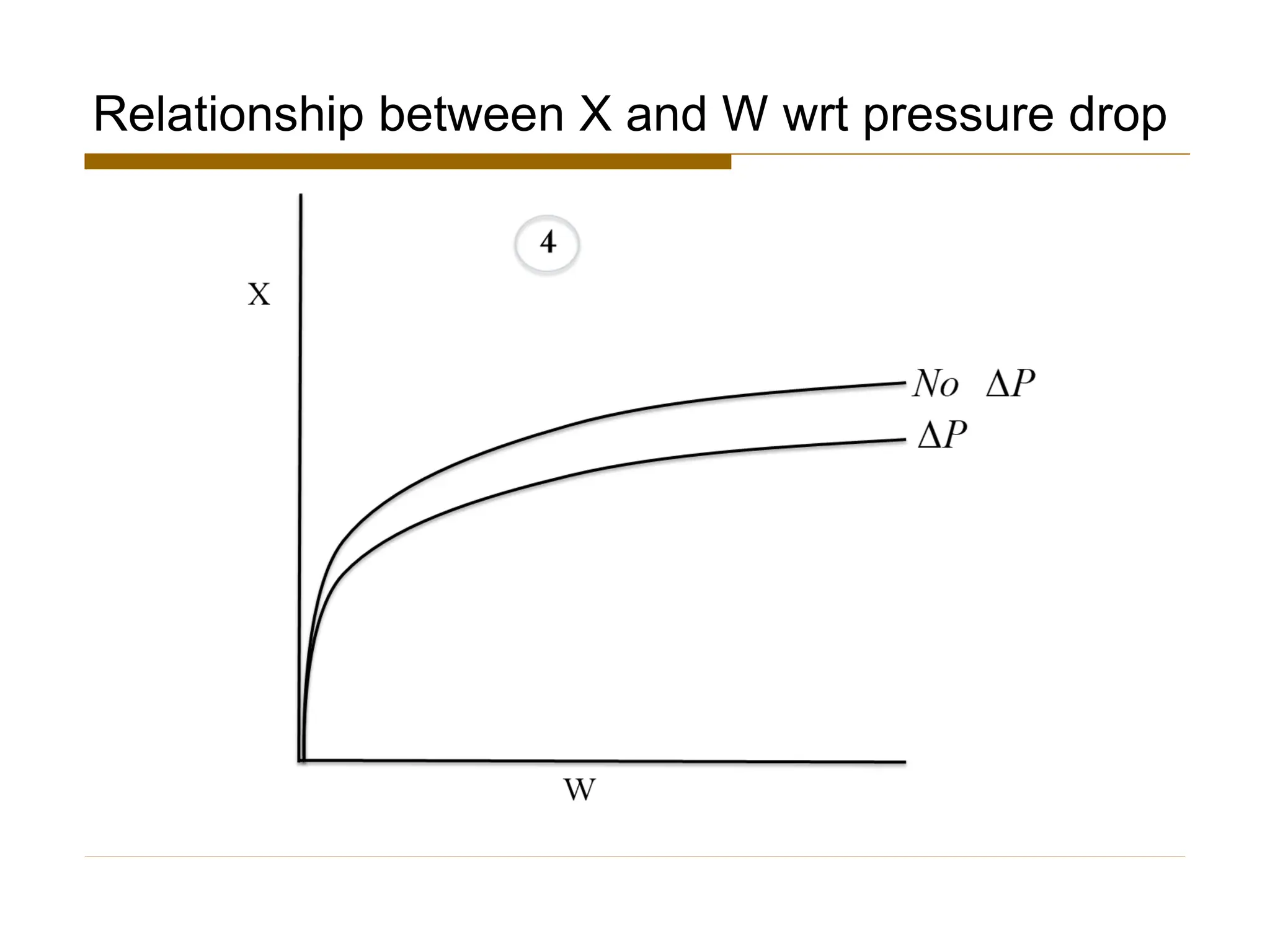
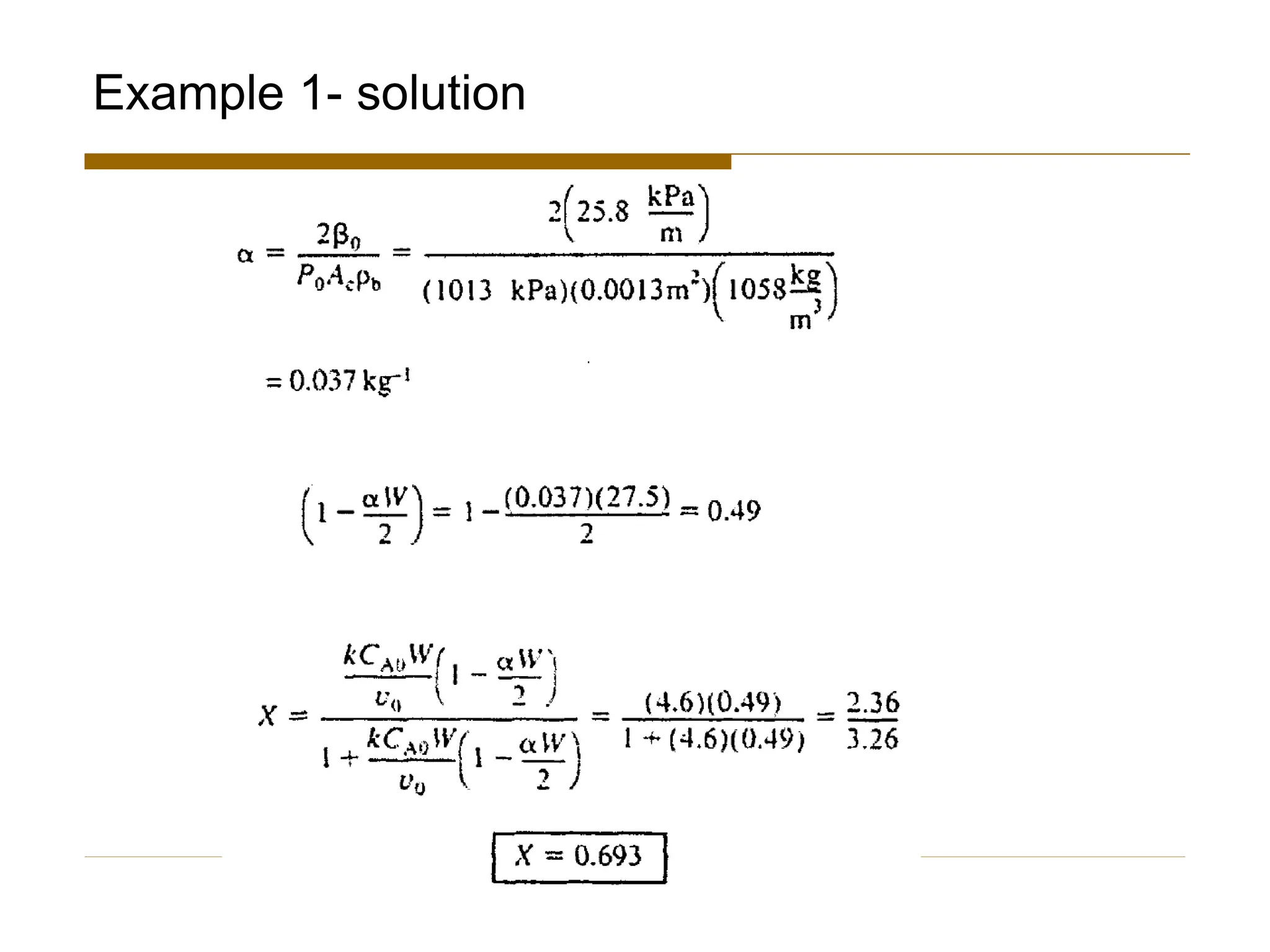
This document provides an overview of packed bed reactor design. It defines a packed bed reactor and lists learning outcomes which include determining catalyst weight, pressure drop parameters, and conversion. Advantages and disadvantages of packed bed reactors are given. Equations for governing reactor sizing are presented, including equations relating volumetric reaction rate, catalyst weight, and pressure drop. The impact of pressure drop on gas versus liquid phase reactions is discussed. The Ergun equation for calculating pressure drop is derived. Finally, an example problem is given to demonstrate the effect of pressure drop on conversion.

1. Lecture 9: Packed bed reactor design
CHE 62104 Chemical Reaction Engineering
Dr. Firnaaz Ahamed
Firnaaz.ahamed@taylors.edu.my
1

2. What is a packed bed reactor?
 A fixed bed reactor
usually consists of a
cylindrical vessel
packed with
catalyst pellets and
easy to design and
operate.
Catalyst
Inert balls
Feed
Product
 The metal support
grid and screen is
placed near the
bottom to support
the catalyst.
 Inert ceramic balls
are placed above
the catalyst bed to
distribute the feed
evenly.

3. Learning outcomes
At the end of the lesson, you should be able to :
 Design the packed bed reactor
◼ determine the weight of the catalyst
◼ determine pressure drop parameters
◼ determine conversion in the packed bed reactor
◼ study the effect of pressure drop on reaction rate
catalyst weight and conversion
3

4. Pros and cons of a packed bed reactor
Advantages Disadvantages
• Ideal plug flow behavior
• Lower maintenance cost
• Reduced loss due to attrition
and wear.
• The regeneration or
replacement of catalyst is
difficult, process needs to be
shutdown.
• Plugging of bed due to coke
deposition which results in
high pressure drop.

5.  Catalyst pellet sizes are usually in the range of 1 to 10 mm. Non-
uniform packing of catalysts can cause channeling of fluids
leading to poor heat and mass transfer.
 The bed voidage is usually:
Hollow cylinder of thin wall thickness ( ~ 0.6 – 0.8)
Sphere ( ~ 0.37 – 0.4)
Solid cylinder ( ~ 0.35)
 For better heat management for very highly exothermic (or
endothermic) reaction the multi-tubular reactor is used with
catalyst packed inside the tubes. The cooling (or heating) fluid
flows through the shell side.
Features of packed bed reactor

6. Multi-tubular
reactor
Features of packed bed reactor

7. Governing equations for sizing a packed bed
reactor (PBR)
 A general PFR is given as:
 In a PBR, catalyst weight is related to the volume as:
 The volumetric reaction rate is also related to the reaction
rate per unit mass of catalyst as:
𝑑𝑉
𝑑𝑋
=
𝐹𝐴0
−𝑟𝐴
𝑊 = 𝜌𝑏𝑉 = 1 − 𝜀 𝜌𝑐𝑉
kg = kg/m3 m3
−𝑟𝐴 = 𝜌𝑏 −𝑟𝐴
′
Τ
mol m3. s = kg/m3 Τ
mol kg. s

8. Governing equations for sizing packed bed
reactor
 A general PBR is given as:
𝑑𝑊
𝑑𝑋
=
𝐹𝐴0
−𝑟𝐴
′
𝑊 = 𝐹𝐴0 න
0
𝑋
1
−𝑟𝐴
′ 𝑑𝑋

9. The effect of pressure drop is negligible in liquid
phase reactions
In liquid phase reactions, concentrations of the reactants
are insignificantly affected by even large changes in the total
pressure. Thus, effect of pressure drop can be ignored
when sizing liquid phase reactors.
𝑑𝑊
𝑑𝑋
=
𝐹𝐴0
−𝑟𝐴
′
𝑊 = 𝐹𝐴0 න
0
𝑋
1
−𝑟𝐴
′ 𝑑𝑋

10. Pressure drop must be considered for gas phase
reactions
In gas phase reactions the concentration of the reacting
species is proportional to the total pressure, thus pressure
drop is a key factor in success or failure of the reactor
operation.
Consider a second order isomerisation gas phase reaction in
a packed bed reactor:

11. Pressure drop must be considered for gas phase
reactions
The concentration of the reactants must consider the changes
in pressure and temperature:
The rate of reaction is:

12. Pressure drop must be considered for gas phase
reactions
If isothermal operation (𝑇 = 𝑇0):
The pressure drop is given as:

13. Solving for catalyst weight (second order
reaction, variable volume, and isothermal)
𝑑𝑊
𝑑𝑋
=
𝐹𝐴0
−𝑟𝐴
′
𝑑𝑊
𝑑𝑋
=
𝑣0𝐶𝐴0
𝑘𝐶𝐴
2
𝑑𝑊
𝑑𝑋
=
𝑣0𝐶𝐴0 1 + 𝜀𝑋 2
𝑘𝐶𝐴0
2
1 − 𝑋 2𝑦2
𝑑𝑊
𝑑𝑋
=
𝑣0 1 + 𝜀𝑋 2
𝑘𝐶𝐴0 1 − 𝑋 2 1 − 𝛼𝑊
න
0
𝑊
1 − 𝛼𝑊 𝑑𝑊 =
𝑣0
𝑘𝐶𝐴0
න
0
𝑋
1 + 𝜀𝑋 2
1 − 𝑋 2
𝑑𝑋

14. For a second order reaction with no variable
volume and isothermal

15. Once we solve for catalyst weight, we can size
the reactor
𝑊 = 𝜌𝑏𝑉
𝑊 = 1 − 𝜀 𝜌𝑐𝑉
𝑊 = 1 − 𝜀 𝜌𝑐𝐴𝑐𝑧

16. What if the reactor is
NOT operated isothermally
or
temperature changes CANNOT be neglected?

17. Pressure drop across a packed bed can be
computed using Ergun equation
Majority of the gas phase reactions are carried out by passing
the reactants through a bed of catalyst particles.
Ergun equation is widely used to calculate pressure drop in a
packed porous bed (fixed bed) reactor.








+
−





 −
−
= G
D
D
g
G
dz
dP
p
p
c
75
.
1
)
1
(
150
1
2
3





Laminar
flow
Turbulent
flow

18. A
m
G
•
=
= 9.81 m/s2
ε
ε

19. Pressure drop using Ergun equation
In calculating the pressure drop using Ergun equation, the
only parameter that changes on right hand side is gas density.
At steady state
Recall
Combining
Simplifying








+
−
−
−
= G
D
D
g
G
dz
dP
p
p
c
75
.
1
)
1
(
150
)
1
(
3
0





𝛽𝑜 =
ሻ
𝐺(1 − 𝜀
𝜌𝑜𝑔𝑐𝐷𝑝𝜀3
150(1 − 𝜀ሻ𝜇
𝐷𝑝
+ 1.75𝐺

20. Pressure drop using Ergun equation
Recall
Thus, the Ergun equation can be modified in terms of weight
of the catalyst
Simplified
𝑊 = 1 − 𝜀 𝜌𝑐𝐴𝑐𝑧

21. Pressure drop using Ergun equation
Recall
Final differential form of Ergun equation for pressure drop in
packed beds

22. Relationship between P and W

23. Relationship between CA and W wrt pressure
drop

24. Relationship between -rA and W wrt pressure
drop

25. Relationship between X and W wrt pressure drop

26. What is the effect of catalyst size (Dp) and reactor
cross-sectional area (Ac) on the performance?
 Refer to relationship between the parameters in the
following equation:
 For turbulent flow:
 Laminar flow:








+
−
= G
D
P
D
g
A
G
p
p
c
c
c
75
.
1
)
1
(
150
2
0
3
0







27. Example 1
 The reactor is 20 m length with a cross sectional area of 0.0013 m2.
Experiment is conducted to study the effect of particle size on
conversion profile. However, it is assumed that the rate constant is
unaffected by the particle size.
Data:
Initial pressure, Po = 10 atm = 1013 kPa
Entering volumetric flow rate, vo = 7.15 m3/h
Catalyst pellet size, Dp = 0.006 m
Catalyst density, 𝜌𝑝=1923 kg/m3
Pressure drop parameter, 𝛽𝑜=25.8 kPa/m
Molar flow rate = 0.1 kmol/m3
𝑘 = 12
𝑚6
𝑘𝑚𝑜𝑙. 𝑘𝑔 𝑐𝑎𝑡. ℎ
Predict the changes on reaction conversion due to pressure drop effects
(compute X under the condition of with and without pressure drop.)

28. Example 1- solution
28
ε)=

29. Example 1- solution

30. Example 1- solution

31. Conclusion
 Able to design packed bed reactor parameters such
as conversion, weight of the catalyst bed etc.
 Able to relate pressure drop with rate law and weight
of the bed