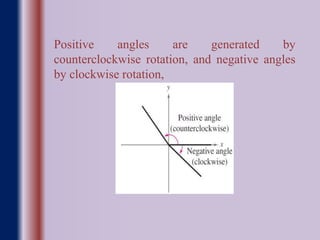
This document provides an overview of trigonometry including: - Definitions of measuring angles in radians and degrees, and conversions between the two units. - Definitions of the six circular functions (sine, cosine, tangent, cosecant, secant, cotangent) and how they relate to positions on a unit circle. - Examples of deriving the values of the six circular functions for a given angle. - Important trigonometric identities like the Pythagorean identity of sine and cosine. - A table of the values of the six trigonometric functions for common angles from 0 to 90 degrees.

1. TRIGNOMETRY
LECTURE 7
MISS. RIFAT JABEEN
25-Mar-2022

2. At the end of this section students should
be able to know
• Measure of angle in radian and degree
• Definition of circular function
• Derivation of circular functions for simple
cases

3. TRIGNOMETRY
Trigonometry, the branch of mathematics
concerned with specific functions of
angles and their application to calculations.
There are six trigonometric ratios, sine,
cosine, tangent, cosecant, secant and
cotangent. These six trigonometric ratios
are abbreviated as sin, cos, tan, cosec, sec,
cot.

4. An angle is determined by rotating a ray (half-line) about
its endpoint. The starting position of the ray is the initial
side of the angle, and the position after rotation is the
terminal side, .
ANGLES:-

5. Positive angles are generated by
counterclockwise rotation, and negative angles
by clockwise rotation,

6. Measure of Angles in Radian

9. Degree – Radian Conversion

11. 1° =
𝜋
180°
60° = 60 ×
𝜋
180°
=
𝜋
3
radian
60° =1.047 radian

13. 𝜋
6
=
𝜋
6
×
180
𝜋
= 30°

15. • Definition of circular function
• Derivation of circular functions for simple cases

16. Definition of circular function
circular functions are part of the set of
trigonometric functions. Each arc length s
determines a single ordered pair (cos s, sin s) on a
unit circle. Both s and cos s are real numbers and
define a function (s, cos s) which is called the
circular function cosine. Likewise, s and sin s are
real numbers and define a function (s, sin s) which
is called the circular function sine. These functions
are called circular functions since both cos s and
sin s are coordinates on a unit circle.

19. EXAMPLE:-
from point A(1,0) to point P is q units. What are the values of the six
circular functions of q?
Solution :
sin q =
1
3
and cos q=
√8
3
tan 𝑞 =
sin 𝑞
cos 𝑞
=
1/3
√8/3
=
1
√8
c𝑜 𝑡 𝑞 =
cos 𝑞
sin 𝑞
=
8
3
1
3
= 8
sec 𝑞 =
1
cos 𝑞
=
1
√8/3
=
3
√8
c𝑜𝑠𝑒𝑐 𝑞 =
1
sin 𝑞
=
1
1
3
= 3

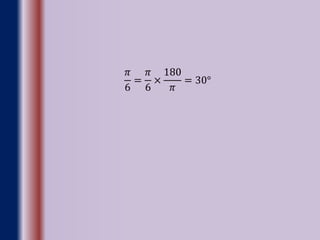
20. Pythagorean Identities
When the Pythagoras theorem is expressed in the form of trigonometry
functions, it is said to be Pythagorean identity. There are majorly three
identities:
•sin2 x + cos2 x = 1 [Very Important]
•1+tan2 x = sec2 x
•cosec2 x = 1 + cot2 x
Trigonometric
Ratios/
angle= θ in
degrees
0 ° 30 ° 45 ° 60 ° 90 °
Sin θ 0 1/2 1/√2 √3/2 1
Cos θ 1 √3/2 1/√2 1/2 0
Tan θ 0 1/√3 1 √3 ∞
Cosec θ ∞ 2 √2 2/√3 1
Sec θ 1 2/√3 √2 2 ∞
Cot θ ∞ √3 1 1/√3 0
Table
The trigonometric ratio table for six functions like Sin, Cos, Tan, Cosec,
Sec, Cot, are: