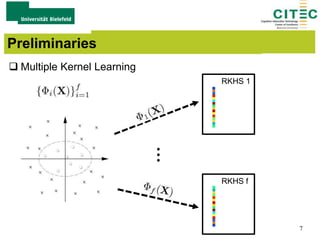
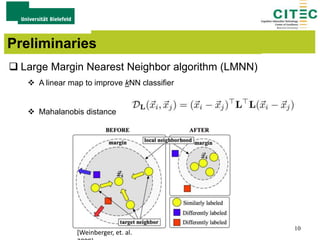
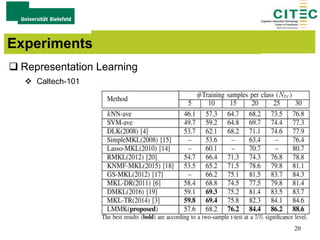
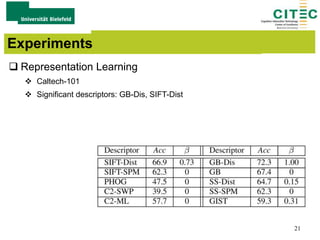
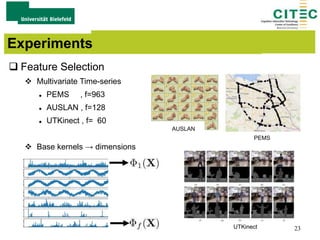
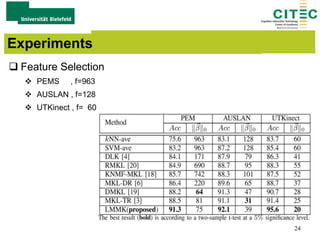
The document outlines a method for large-margin multiple kernel learning (LMMK) aimed at enhancing discriminative feature selection and representation learning in machine learning approaches. It discusses the optimization framework, local class separation in Reproducing Kernel Hilbert Space (RKHS), and details various experiments conducted with different datasets. Key techniques include the use of multiple base kernels and non-negative linear programming for effective feature selection and representation.

1. Large-Margin Multiple Kernel Learning
for
Discriminative Features Selection and
Representation Learning
Babak Hosseini, Barbara Hammer
IJCNN 2019, 14-19 July
Machine Learning Group
https://www.cit-ec.de/en/ML

2.  Classification and retrieval
Numerous representations (SIFT, HOG, GIST, … )
Hundreds of features (Joints, sensors)
Introduction
2

3.  Classification and retrieval
Goal:
 Improving accuracy
 Small selection set
Introduction
3

4.  Preliminaries
 LMMK algorithm
 Experiments
 Summary
Outline
4

5.  Preliminaries
 LMMK algorithm
 Experiments
 Summary
5

6.  Multiple Kernel Learning
 Map data to feature space
 Multiple transfers to RKHS
Preliminaries
6

7.  Multiple Kernel Learning
Preliminaries
RKHS 1
RKHS f
7

8.  Multiple Kernel Learning
 Base kernels:
 Different representations
 Feature selection
Preliminaries
8

9.  Multiple Kernel Learning
 Optimal combination of base kernels
 Optimization problem:
Preliminaries
9

10.  Large Margin Nearest Neighbor algorithm (LMNN)
 A linear map to improve kNN classifier
 Mahalanobis distance
Preliminaries
[Weinberger, et. al.
10

11.  Large Margin Nearest Neighbor algorithm (LMNN)
 Convex optimization problem
Preliminaries
11

12.  Preliminaries
 LMMK algorithm
 Experiments
 Summary
12

13.  Large Margin Multiple Kernel Learning (LMMK)
 Local separation of classes in RKHS
 Mahalanobis distance in RKHS
 B is diagonal
 : m-th entry of diagonal → weight of the m-th representation
LMMK Algorithm
𝛽 𝑚
13

14.  Large Margin Multiple Kernel Learning (LMMK)
 Local separation of classes in RKHS
 Sparse Combination of base kernels
LMMK Algorithm
14

15.  Large Margin Multiple Kernel Learning (LMMK)
 Local separation of classes in RKHS
 Sparse Combination of base kernels
 Non-negative for interpretation
LMMK Algorithm
𝛽
15

16.  Optimization framework
 Non-negative Linear programming
 LP solvers: YALMIP, CVX, etc.
LMMK Algorithm
16

17.  Preliminaries
 LMMK algorithm
 Experiments
 Summary
17

18.  Representation Learning
 Datasets
 Caltech-101
 Pascal VOC 2007
 Oxford Flowers17
Experiments
Caltech-101
Pascal VOC 2007
Oxford Flowers17
18

19.  Representation Learning
 Datasets
 Caltech-101
 Pascal VOC 2007
 Oxford Flowers17
 Base kernels → descriptors
Experiments
19

20.  Representation Learning
 Caltech-101
Experiments
20

21.  Representation Learning
 Caltech-101
 Significant descriptors: GB-Dis, SIFT-Dist
Experiments
21

22.  Representation Learning
 Pascal VOC 2007
 Oxford Flowers17
Experiments
22

23.  Feature Selection
 Multivariate Time-series
 PEMS , f=963
 AUSLAN , f=128
 UTKinect , f= 60
 Base kernels → dimensions
Experiments
AUSLAN
PEMS
UTKinect 23

24.  Feature Selection
 PEMS , f=963
 AUSLAN , f=128
 UTKinect , f= 60
Experiments
24

25.  Preliminaries
 LMMK algorithm
 Experiments
 Summary
2
5

26.  A new multiple kernel learning
 Diagonal metric in RKHS
 Linear programming optimization framework
 -norm sparsity leading to compact kernel combination
 Discriminative feature selection
Summary
𝑙1
26

27. Thank you very much!
Questions?
27