Koleksi soalan addmath kertas1

Koleksi Soalan-Soalan
Percubaan add math SPM
kertas 1

Disusun:
http://kampungebuku.blogspot.com

Daftar Isi
Koleksi Soalan-Soalan Percubaan Add Math Kertas 1
1. Peperiksaan Percubaan Sekolah Berasrama Penuh ……1
2. Jawapan Peperiksaan Percubaan SBP…………………. 19
3. Peperiksaan Percubaan Negeri Perak………………….. 25
4. Jawapan Peperiksaan Percubaan Negeri Perak ……… 41
5. Peperiksaan Percubaan Negeri Selangor ……………... 46
6. Jawapan Peperiksaan Percubaan S’ngor ……………. 71
7. Peperiksaan Percubaan Negeri Terengganu…………. 74
8. Jawapan Peperiksaan Percubaan T’gganu …………... 98

Name : ………………..…………… Form : ………………………..……

BAHAGIAN PENGURUSAN SEKOLAH BERASRAMA PENUH
DAN SEKOLAH KLUSTER
KEMENTERIAN PELAJARAN MALAYSIA

PEPERIKSAAN PERCUBAAN SELARAS SPM 2009 3472 / 1
ADDITIONAL MATHEMATICS
Kertas 1
Ogos 2009
2 jam Dua jam

Untuk Kegunaan Pemeriksa
JANGAN BUKA KERTAS SOALAN INI
Soalan Markah Markah
SEHINGGA DIBERITAHU Penuh Diperolehi
1 2
1. Tulis nama dan tingkatan anda pada
2 4
ruangan yang disediakan.
3 4
2. Kertas soalan ini adalah dalam 4 3
dwibahasa. 5 2
6 3
3. Soalan dalam bahasa Inggeris 7 3
mendahului soalan yang sepadan 8 3
dalam bahasa Melayu. 9 4
10 3
4. Calon dibenarkan menjawab 11 3
keseluruhan atau sebahagian soalan 12 4
sama ada dalam bahasa Inggeris atau 13 3
bahasa Melayu. 14 3
15 3
5. Calon dikehendaki membaca 16 3
maklumat di halaman belakang kertas 17 4
soalan ini. 18 4
19 3
20 3
21 3
22 3
23 3
24 3
25 4

TOTAL 80

Kertas soalan ini mengandungi 18 halaman bercetak

3472/1 2009 Hak Cipta SBP [Lihat sebelah
SULIT
http://kampungebuku.blogspot.com 1

SULIT 2 3472/1

The following formulae may be helpful in answering the questions. The symbols given are the ones
commonly used.
ALGEBRA
2
−b ± b − 4ac log c b
1 x= 8 logab =
2a log c a

2 am × an = a m + n 9 Tn = a + (n-1)d

3 am ÷ an = a m - n
n
10 Sn = [2a + ( n − 1) d ]
2
4 (am) n = a nm 11 Tn = ar n-1
5 loga mn = log am + loga n a(r n − 1) a (1 − r n )
12 Sn = = , (r ≠ 1)
m r −1 1− r
6 loga = log am - loga n
a
n 13 S ∞ = , r <1
7 log a mn = n log a m 1− r

CALCULUS

dy dv du
1 y = uv , =u +v 4 Area under a curve
dx dx dx b

du dv
= ∫ y dx or
v −u a
u dy
2 y= , = dx 2 dx , b

v dx v = ∫ x dy
a

dy dy du 5 Volume generated
3 = × b
dx du dx = ∫ π y 2 dx or
a
b
2
= ∫π x dy
a

GEOMETRY

1 Distance = ( x 2 − x1 ) 2 + ( y 2 − y1 ) 2 5 A point dividing a segment of a line
⎛ nx + mx2 ny1 + my 2 ⎞
( x,y) = ⎜ 1 , ⎟
2 Midpoint ⎝ m+n m+n ⎠
⎛ x1 + x 2 y + y2 ⎞
(x , y) = ⎜ , 1 ⎟
⎝ 2 2 ⎠ 6 Area of triangle
1
3 r = x2 + y2 = ( x1 y 2 + x 2 y 3 + x3 y11 ) − ( x 2 y1 + x3 y 2 + x1 y 3 )
2
xi + yj
4 ˆ
r=
x2 + y2

3472/1 2009 Hak Cipta SBP [ Lihat sebelah
SULIT

SULIT 3 3472/1

STATISTIC

1 x =
∑x ∑ w1 I1
7 I=
N ∑ w1
n!
∑ fx 8 Pr =
n

2 x = (n − r )!
∑f n!
9 n
Cr =
(n − r )!r!
3 σ =
∑ (x − x ) 2

=
∑x 2

−x
_2

N N 10 P(A ∪ B) = P(A)+P(B)- P(A ∩ B)

4 σ=
∑ f ( x − x) 2

= ∑ fx 2
−x
2 11 P (X = r) = nCr p r q n − r , p + q = 1
∑f ∑f
12 Mean µ = np
⎡1 ⎤
⎢2 N −F⎥
5 m = L+⎢ ⎥C 13 σ = npq
⎢ fm ⎥
⎢
⎣ ⎥
⎦ x−μ
14 z=
σ
Q1
6 I= ×100
Q0

TRIGONOMETRY

1 Arc length, s = r θ 9 sin (A ± B) = sinA cosB ± cosA sinB

1 2 10 cos (A ± B) = cosA cosB m sinA sinB
2 Area of sector , L = rθ
2
3 sin 2A + cos 2A = 1 tan A ± tan B
11 tan (A ± B) =
1 m tan A tan B
4 sec2A = 1 + tan2A
a b c
2 2 12 = =
5 cosec A = 1 + cot A sin A sin B sin C

6 sin 2A = 2 sinA cosA
13 a2 = b2 + c2 - 2bc cosA
2 2
7 cos 2A = cos A – sin A
= 2 cos2A - 1 1
= 1 - 2 sin2A 14 Area of triangle = absin C
2

2 tan A
8 tan 2A =
1 − tan 2 A

3472/1 2009 Hak Cipta SBP [ Lihat sebelah
SULIT

SULIT 4 3472/1

THE UPPER TAIL PROBABILITY Q(z) FOR THE NORMAL DISTRIBUTION N(0,1)
KEBARANGKALIAN HUJUNG ATAS Q(z) BAGI TABURAN NORMAL N(0, 1)

1 2 3 4 5 6 7 8 9
z 0 1 2 3 4 5 6 7 8 9
Minus / Tolak
0.0 0.5000 0.4960 0.4920 0.4880 0.4840 0.4801 0.4761 0.4721 0.4681 0.4641 4 8 12 16 20 24 28 32 36
0.1 0.4602 0.4562 0.4522 0.4483 0.4443 0.4404 0.4364 0.4325 0.4286 0.4247 4 8 12 16 20 24 28 32 36
0.2 0.4207 0.4168 0.4129 0.4090 0.4052 0.4013 0.3974 0.3936 0.3897 0.3859 4 8 12 15 19 23 27 31 35
0.3 0.3821 0.3783 0.3745 0.3707 0.3669 0.3632 0.3594 0.3557 0.3520 0.3483 4 7 11 15 19 22 26 30 34
0.4 0.3446 0.3409 0.3372 0.3336 0.3300 0.3264 0.3228 0.3192 0.3156 0.3121 4 7 11 15 18 22 25 29 32
0.5 0.3085 0.3050 0.3015 0.2981 0.2946 0.2912 0.2877 0.2843 0.2810 0.2776 3 7 10 14 17 20 24 27 31
0.6 0.2743 0.2709 0.2676 0.2643 0.2611 0.2578 0.2546 0.2514 0.2483 0.2451 3 7 10 13 16 19 23 26 29
0.7 0.2420 0.2389 0.2358 0.2327 0.2296 0.2266 0.2236 0.2206 0.2177 0.2148 3 6 9 12 15 18 21 24 27
0.8 0.2119 0.2090 0.2061 0.2033 0.2005 0.1977 0.1949 0.1922 0.1894 0.1867 3 5 8 11 14 16 19 22 25
0.9 0.1841 0.1814 0.1788 0.1762 0.1736 0.1711 0.1685 0.1660 0.1635 0.1611 3 5 8 10 13 15 18 20 23
1.0 0.1587 0.1562 0.1539 0.1515 0.1492 0.1469 0.1446 0.1423 0.1401 0.1379 2 5 7 9 12 14 16 19 21
1.1 0.1357 0.1335 0.1314 0.1292 0.1271 0.1251 0.1230 0.1210 0.1190 0.1170 2 4 6 8 10 12 14 16 18
1.2 0.1151 0.1131 0.1112 0.1093 0.1075 0.1056 0.1038 0.1020 0.1003 0.0985 2 4 6 7 9 11 13 15 17
1.3 0.0968 0.0951 0.0934 0.0918 0.0901 0.0885 0.0869 0.0853 0.0838 0.0823 2 3 5 6 8 10 11 13 14
1.4 0.0808 0.0793 0.0778 0.0764 0.0749 0.0735 0.0721 0.0708 0.0694 0.0681 1 3 4 6 7 8 10 11 13
1.5 0.0668 0.0655 0.0643 0.0630 0.0618 0.0606 0.0594 0.0582 0.0571 0.0559 1 2 4 5 6 7 8 10 11
1.6 0.0548 0.0537 0.0526 0.0516 0.0505 0.0495 0.0485 0..0475 0.0465 0.0455 1 2 3 4 5 6 7 8 9
1.7 0.0446 0.0436 0.0427 0.0418 0.0409 0.0401 0.0392 0.0384 0.0375 0.0367 1 2 3 4 4 5 6 7 8
1.8 0.0359 0.0351 0.0344 0.0336 0.0329 0.0322 0.0314 0.0307 0.0301 0.0294 1 1 2 3 4 4 5 6 6
1.9 0.0287 0.0281 0.0274 0.0268 0.0262 0.0256 0.0250 0.0244 0.0239 0.0233 1 1 2 2 3 4 4 5 5
2.0 0.0228 0.0222 0.0217 0.0212 0.0207 0.0202 0.0197 0.0192 0.0188 0.0183 0 1 1 2 2 3 3 4 4
2.1 0.0179 0.0174 0.0170 0.0166 0.0162 0.0158 0.0154 0.0150 0.0146 0.0143 0 1 1 2 2 2 3 3 4
2.2 0.0139 0.0136 0.0132 0.0129 0.0125 0.0122 0.0119 0.0116 0.0113 0.0110 0 1 1 1 2 2 2 3 3
2.3 0.0107 0.0104 0.0102 0 1 1 1 1 2 2 2 2
0.00990 0.00964 0.00939 0.00914 3 5 8 10 13 15 18 20 23
0.00889 0.00866 0.00842 2 5 7 9 12 14 16 16 21
2.4 0.00820 0.00798 0.00776 0.00755 0.00734 2 4 6 8 11 13 15 17 19
0.00714 0.00695 0.00676 0.00657 0.00639 2 4 6 7 9 11 13 15 17
2.5 0.00621 0.00604 0.00587 0.00570 0.00554 0.00539 0.00523 0.00508 0.00494 0.00480 2 3 5 6 8 9 11 12 14
2.6 0.00466 0.00453 0.00440 0.00427 0.00415 0.00402 0.00391 0.00379 0.00368 0.00357 1 2 3 5 6 7 9 9 10
2.7 0.00347 0.00336 0.00326 0.00317 0.00307 0.00298 0.00289 0.00280 0.00272 0.00264 1 2 3 4 5 6 7 8 9
2.8 0.00256 0.00248 0.00240 0.00233 0.00226 0.00219 0.00212 0.00205 0.00199 0.00193 1 1 2 3 4 4 5 6 6
2.9 0.00187 0.00181 0.00175 0.00169 0.00164 0.00159 0.00154 0.00149 0.00144 0.00139 0 1 1 2 2 3 3 4 4
3.0 0.00135 0.00131 0.00126 0.00122 0.00118 0.00114 0.00111 0.00107 0.00104 0.00100 0 1 1 2 2 2 3 3 4

1 ⎛ 1 ⎞ f (z)
f ( z) = exp⎜ − z 2 ⎟ Example / Contoh:
2π ⎝ 2 ⎠ Q(z)
∞ If X ~ N(0, 1), then P(X > k) = Q(k)
Q ( z ) = ∫ f ( z ) dz Jika X ~ N(0, 1), maka P(X > k) = Q(k)
k

O z

[Lihat sebelah
3472/1 SULIT

For SULIT 5 3472/1
examiner’s
use only
Answer all questions.

1 Diagram1 shows a function that maps set A to set B.
Rajah 1 menunjukkan fungsi yang memeta set A ke set B.
x
f x−3

−2 −5

4 m

6 3

Set A Set B

Diagram 1
Rajah 1

It is given that the function that maps set A to set B is f : x → x − 3 .
Diberi bahawa fungsi yang memeta set A ke set B ialah f : x → x − 3 .

Find
Cari
(a) the value of m ,
nilai m ,
−1
(b) the value of ff (3) .
−1
nilai ff (3) . [2 marks]
[ 2markah]

Answer/Jawapan : (a) ……………………..
1
(b).........................................
2
4
2 Given that g : x → , x ≠ 0 and the composite function gf : x → x + 2 , find
x
4
Diberi g : x → , x ≠ 0 dan fungsi gubahan gf : x → x + 2 , cari
x
(a) f (x ) ,
(b) the value of x when fg ( x ) = 6 .
nilai bagi x bila fg ( x ) = 6 . [4 marks]
[4 markah]

2

Answer/Jawapan : (a) ………......……………..
4
(b) ......……………………..

[Lihat sebelah
3472/1 SULIT

For
SULIT 6 3472/1 examiner’s
use only
6 − 2x
3 Given that f : x → 8 − px and g −1 : x → ,
5
6 − 2x
Diberi f : x → 8 − px dan g −1 : x → ,
5

find
cari

(a) g (x ) ,

(b) the value of p if g ( x − 2) = f ( x ) .
nilai p jika g ( x − 2) = f ( x ) .
[4 marks]
[4 markah]

Answer/Jawapan : (a) ………......……………..

(b) ......…………………….. 3

.
4
1 2
4 Given that x = 2 and x = − are the roots of the equation 3x + bx + c = 0 , find the value of
3
b and the value of c .
1 2
Diberi x = 2 dan x = − ialah punca-punca persamaan 3x + bx + c = 0 , cari nilai b
3
dan nilai c .
[3 marks]
[3 markah]

4

3
Answer/ Jawapan : b = ………… c = ………………

[Lihat sebelah
3472/1 SULIT

For SULIT 7 3472/1
examiner’s
use only
5 Find the range of values of x for x 2 + 20 < 9 x .
Cari julat nilai x bagi x 2 + 20 < 9 x .
[2 marks]
[2 markah]

5
Answer/Jawapan :........... ……..........

2

6 Given quadratic function f ( x ) = −[ ( x + 6 p ) 2 − 5 ] + q has a maximum point T ( −3n , 15n 2 ) .
Diberi fungsi kuadratik f ( x ) = −[ ( x + 6 p ) 2 − 5 ] + q mempunyai titik maksimum. T ( −3n , 15n 2 ) .

Express q in terms p.
Nyatakan q dalam sebutan p.
[3 marks]
[3 markah]

6
Answer /Jawapan: ………………………...

3 .

1
7 Solve the equation 25 x + 2 = .
625 x
1
Selesaikan persamaan 25 x + 2 = .
625 x
[3 marks]
[3 markah]

7

3
Answer / Jawapan: …………….…………

[Lihat sebelah
3472/1 SULIT

SULIT 8 3472/1
For
examiner’s
use only
8 Solve the equation log 3 x − log 3 ( x − 2) = −1 .
Selesaikan persamaan log 3 x − log 3 ( x − 2) = −1 .
[3 marks]
[ 3 markah]

8

Answer/Jawapan : ……..……...……….....
3

9 Given log 5 2 = h and log 5 3 = k , express log12 90 in terms of h and k .
Diberi log 5 2 = h dan log 5 3 = k , ungkapkan log12 90 dalam sebutan h dan k .

[4 marks]
[4 markah]

9

Answer/ Jawapan : ……………...………................
4

10 It is given an arithmetic progression is 5 , 7 , 9 , ………., 87. Find the number of terms of this
progression.
Diberi bahawa suatu janjang aritmetik ialah 5 , 7 , 9 , ………., 87 . Cari ilangan sebutan
dalam janjang itu..

[3 marks]
[ 3 markah]

10

Answer/Jawapan: …...…………..….................... 3

[Lihat sebelah
3472/1 SULIT

SULIT 9 3472/1
For
examiner’s
use only 1 1 1
11 It is given the first three terms of a geometric series are + + + ……….Find the sum to
9 27 81
infinity of the series.
1 1 1
Diberi bahawa tiga sebutan pertama dalam siri geometri ialah + + + ……….Cari
9 27 81
hasiltambah hingga sebutan ketakterhinggaan siri itu..
[3 marks]
[3 markah]

11
1
Answer/Jawapan: : ……………...……….....
3

12 The variables x and y are related by the equation y = px 2 + 2 x + 5q , where p and q are
constants.
2
Diagram 12 shows a straight line graph ( y − 2 x ) against x .

Pembolehubah x dan y dihubungkan oleh persamaan y = px 2 + 2 x + 5q , dengan keadaan
p dan q ialah pemalar.
2
Rajah 12 menunjukkan graph ( y − 2 x ) melawan x .
y − 2x
(4,3)

O x2

−5

Diagram 12
Rajah 12
Find the value of p and of q .
Cari nilai p dan nilai q .

[4 marks]
12 [ 4 markah]

4

Answer : p = ……….… q = ………………….

[Lihat sebelah
3472/1 SULIT

SULIT 10 3472/1

For
y x examiner’s
13 Diagram 13 shows a straight line PQ with the equation − = 1. use only
8 6
y x
Rajah 13 menunjukan garis lurus PQ yang mempunyai pesamaan − = 1.
8 6

y

P•

•
Q O x

Diagram 13
Rajah 13
Find the equation of the straight line which is perpendicular to PQ and passes through the
point Q.
Cari persamaan garislurus yang berserenjang dengan PQ dan melalui titik Q.
[ 3 marks]
[3 markah]

13

3

Answer/ Jawapan : ……….…………………….

[Lihat sebelah
3472/1 SULIT

For
examiner’s SULIT 11 3472/1
use only

14 Diagram 14 shows A,B and C are three points on a straight line .

Rajah 14 menunjukkan A , B dan C merupakan tiga titik yang terletak di atas garis lurus.

y
• B( x , y )

• C (2,3)
• A(0,2)

O x

Diagram 14
Rajah 14

It is given that 5AC = AB . Find the coordinates of B.
Diberi 5AC = CB. Cari koordinat B.
[ 3 marks]
[ 3 markah]

14

Answer/Jawapan : ………..………..
3
→ →
15 Given PQ = 3 x − 2 y and QR = (1 − h) x + 4 y . The points P , Q and R are collinear.
~ ~ ~
~
→ →
Diberi PQ = 3 x − 2 y dan QR = (1 − h) x + 4 y . Titik-titik P , Q dan R adalah segaris.
~ ~ ~ ~
Find the value of h .
Cari nilai h .

[ 3 marks]
[3 markah]

15

3
Answer/Jawapan :…………………..…..

[Lihat sebelah
3472/1 SULIT

SULIT 12 3472/1
For
examiner’s
use only
16 Solution by graph is not accepted for this question.
Penyelesaian secara graf tidak diterima bagi soalan ini.
→ →
Diagram 16 shows OABC is a parallelogram such that OA = 4i + 3j and OB = 11i + 5j,

Rajah 16 menunjukan OABC ialah sebuah segiempat selari dengan keadaan
→ OA = 4i + 3j
→
dan OB = 11i + 5j,

y
B

C

A

O x
Diagram 16
Rajah 16

→
Find the unit vector in the direction of OC .
→
Cari vektor unit pada arah OC .
[3 marks]
[ 3 markah]

16

Answer/Jawapan:…………………………..… 3

[Lihat sebelah
3472/1 SULIT

SULIT 13 3472/1

For
examiner’s
use only
17 Solve the equation 3 cos 2 x + sin 2 x = 0 for 0o ≤ x ≤ 360o

Selesaikan persamaan 3 kos 2 x + sin 2 x = 0 bagi 0 o ≤ x ≤ 360 o
[4 marks]
[4 markah]

17

Answer /Jawapan : ………..……….………
4
18 Diagram 18 shows a semicircle PQR with center O.
Rajah 18 menunjukkan sebuah semibulatan PQR berpusat O.

Q

θ
P O R
Diagram 18
Rajah 18

It is given that the arc length PQ is 6.5 cm and the radius of the semicircle is 5 cm.
Diberi bahawa panjang lengkuk PQ ialah 6.5 cm dan jejari semibulatan ialah 5 cm.
[ Use / Guna π = 3.142 ]

Find
Cari
(a) the value of θ in radian ,
nilai θ dalam radian,

(b) area , in cm2 , of sector QOR.
luas , dalam cm 2, sektor QOR. [4 marks]
[4 markah]

18

3 Answer / Jawapan : (a) …..……..................

(b).................................

[Lihat sebelah
3472/1 SULIT

SULIT 14 3472/1

For
examiner’s
19 Given that f ( x) = x 3 (5 − 3 x) 2 , find f ' (2). use only
Diberi f ( x) = x 3 (5 − 3 x) 2 , cari f ' (2).

[3 marks]
[ 3 markah]

19
0
Answer/Jawapan : ......................................... 3

2
20 Two variables P and x are related by the equation P = 3 x + . Given x increases
x
at a constant rate of 4 units per second when x = 2, find the rate of change of P.
2
Dua pembolehubah P dan x dihubungkan dengan persamaan P = 3 x + .
x
Diberi x bertambah dengan kadar malar 4 unit sesaat apabila x = 2, cari
kadar perubahan bagi P.
[3 marks]
[3 markah]

20

Answer / Jawapan : …...…………..……..…...
3

[Lihat sebelah
3472/1 SULIT

SULIT 15 3472/1

For 3
h dy
examiner’s
21 Given y = 3
and = g (x) , find the value of h if ∫ [ g ( x) + 1]dx = 7.
use only (2 x − 5) dx 2

3
h dy
Diberi y = 3
dan = g (x) , cari nilai bagi h jika ∫ [ g ( x) + 1]dx = 7.
(2 x − 5) dx 2

[3 marks]
[3 markah ]

21

Answer/Jawapan: ..…………........……..
3

22 The mean of a set of data 2m – 3 , 8 , m+1 is 7.
Min bagi set data 2m – 3 , 8 , m+1 ialah 7.

Find
Cari

(a) the value of m ,
nilai m,

(b) the new mean if each of the data multiflied by 3.
Cari min yang baru jika setiap data didarabkan dengan 3.
[3 marks]
[ 3 markah]

22
Answer /Jawapan (a) ..…………........……........
3
[Lihat sebelah
3472/1 SULIT

SULIT 16 3472/1

(b).............................................. For
23 Bag A contains 1 green pen, 2 red pens and 3 blue pens. Bag B contains 2 black erasers examiner’s
and 3 white erasers. Bag C contains 6 gift cards labeled 1, 2, 3, 4, 5 and 6. An item is use only
picked randomly from each bag.
Beg A mengandungi 1 pen hijau, 2 pen merah dan 3 pen biru. Beg B mengandungi 2
pemadam hitam dan 3 pemadam putih. Beg C mengandungi 6 kad hadiah yang dilabel
1, 2, 3, 4, 5 dan 6. Satu item diambil secara rawak daripada setiap beg.

Find the probability of getting a blue pen, a black eraser and a gift card with a number
less than 3.
Cari kebarangkalian mendapat satu pen biru, satu pemadam hitam dan satu kad hadiah
yang berlabel nombor kurang daripada 3.

[3 marks]
[3 markah]

23
Answer /Jawapan: ...…..……..……..…....
3

2
24 The probability that it will rain on a particular day is .
5
If X is the number of rainy days in a week, find

2
Kebarangkalian bahawa hujan akan turun pada sebarang hari ialah .
5
Jika X ialah bilangan hari hujan turun dalam seminggu, cari

(a) the mean of the distribution of X,
min bagi taburan X,

(b) the standard deviation of the distribution of X.
sisihan piawai bagi taburan X.
[3 marks]
[ 3 markah]

24
Answer/ Jawapan: (a)………..……………..
3
[Lihat sebelah
3472/1 SULIT

SULIT 17 3472/1

For (b) ………………….….
examiner’s
use only 25 Diagram 25 shows a standardized normal distribution graph.
Rajah 25 menunjukkan satu graf taburan normal piawai.
f(z)

0.7286

z
-k O k
Diagram 25
Rajah 25

The probability represented by the area of the shaded region is 0.7286.
Kebarangkalian yang diwakili oleh luas kawasan berlorek ialah 0.7286.

(a) Find the value of k,
Cari nilai k,

(b) X is a continuous random variable which is normally distributed with a mean
of μ and a standard deviation of 8. Find the value of μ if X = 70 when the z-score is k.

X ialah pembolehubah rawak selanjar bertaburan secara normal dengan min μ
dan sisihan piawai 8. Cari nilai μ jika X = 70 apabila skor-z ialah k.
[4 marks]
[4 markah]

25

4
Answer/Jawapan : (a)......……...…..……..…...

(b) ...…………..……..….

[Lihat sebelah
3472/1 SULIT

SULIT 18 3472/1

END OF THE QUESTION PAPER
INFORMATION FOR CANDIDATES
MAKLUMAT UNTUK CALON

1. This question paper consists of 25 questions
Kertas soalan ini mengandungi 25 soalan

2. Answer all questions.
Jawab semua soalan

3. Write your answers in the spaces provided in the question paper.
Tulis jawapan anda dalam ruang yang disediakan dalam kertas soalan.

4. Show your working. It may help you to get marks.
Tunjukkan langkah-langkah penting dalam kerja mengira anda. Ini boleh membantu anda untuk
mendapatkan markah.

5. If you wish to change your answer, cross out the answer that you have done.
Then write down the new answer.
Sekiranya anda hendak menukar jawapan, batalkan jawapan yang telah dibuat.
Kemudian tulis jawapan yang baru.

6. The diagrams in the questions provided are not drawn to scale unless stated.
Rajah yang mengiringi soalan tidak dilukis mengikut skala kecuali dinyatakan.

7. The marks allocated for each question are shown in brackets.
Markah yang diperuntukkan bagi setiap soalan ditunjukkan dalam kurungan.

8. A list of formulae is provided on pages 3 to 5.
Satu senarai rumus disediakan di halaman 3 hingga 5.

9. A booklet of four-figure mathematical tables is provided.
Sebuah buku sifir matematik empat angka disediakan.

10. You may use a non-programmable scientific calculator.
Anda dibenarkan menggunakan kalkulator saintifik yang tidak boleh diprogram.

11. Hand in this question paper to the invigilator at the end of the examination.
Serahkan kertas soalan ini kepada pengawas peperiksaan di akhir peperiksaan.

[Lihat sebelah
3472/1 SULIT


SULIT
3472/1
Additional
Mathematics
Kertas 1
Peraturan
Pemarkahan
August
2009

BAHAGIAN PENGURUSAN
SEKOLAH BERASRAMA PENUH DAN SEKOLAH KLUSTER
KEMENTERIAN PELAJARAN MALAYSIA
PEPERIKSAAN PERCUBAAN
SIJIL PELAJARAN MALAYSIA 2009

PEPERIKSAAN PERCUBAAN SPM
TAHUN 2009

KERTAS 1

PERATURAN PEMARKAHAN

UNTUK KEGUNAAN PEMERIKSA SAHAJA


Question Working / Solution Marks Total
1 (a) 1 1 2

1 (b) 3 1

2 (a) 4 2 4
f ( x) = , x ≠ −2
x+2
4 4
g −1 = , x ≠ 0 or =x+2 B1
x f ( x)

2(b) x = −3 2
4 B1
4
+2
x
3(a) 6 − 5x 2 4
g ( x) =
2

6 − 2x
=y B1
5
5
(b) p= 2
2
6 − 5( x − 2)
= 8 − px B1
2
4 b = - 5 and c = - 2 3 3

b = - 5 or c = - 2 B2
5 2
( x – 2) ( 3x + 1) = 0 OR x 2 − x − = 0
3 3 B1

5 4< x<5 2
2
( x − 5)( x − 4) < 0 OR x
4 5
B1
Must indicate the range
correctly by shading or other
method

or
4 5


6 q = 60 p − 5 2 3 3
q = 15( 2 p ) 2 − 5
B2
− 6 p = −3n or 5 + q = 15n 2 B1
7 2 3 3
−
3

2 ( x + 2) = − 4 B2

B1
5 2 ( x + 2 ) or 5 −4 x OR 25 −2 x
8 −1 3 3
x 1
=
x−2 3 B2
⎛ x ⎞
log⎜ ⎟ B1
⎝ x −2⎠

9 2k + h + 1 4 4
2h + k

2 log 5 3 + log 5 2 + log 5 5 B3
2 log 5 2 + log 5 3

log 5 2 2 + log 5 2 + log 5 5 or log 5 2 2 + log 5 3 or B2
log 12 3 + log 12 2 + log 12 5
2

log 5 90
or 2 log 5 3 or 2 log52
log 5 12 B1

10 n = 42 3 3
5 + ( n − 1)( 2) = 87 B2
d=2
B1
11 1 3 3
6
1
9
B2
1
1−
3
1 B1
r=
3


12 p = 2 and q = −1 4 4
p = 2 or q = −1 B3
3 − (−5)
p= or 5q = −5 B2
4−0 B1
y − 2 x = px 2 + 5q
13 3 9 3 3
y = x−
4 2

3 B2
y − 0 = − ( x + 6)
4
3
P ( 0,8) or Q (-6,0) or m ⊥ PQ = − B1
4
14 (10, 7) 3 3

x = 10 or y = 7 B2
x+0 y+8
= 2 or =3 B1
5 5
15 h=7 3 3
1
4λ = −2 or 3 = − (1 − h)
2 B2

⎛ 3 ⎞ ⎛1 − h ) ⎞
⎜ ⎟ = λ⎜
⎜ − 2⎟ ⎜ 4 ⎟ ⎟ B1
⎝ ⎠ ⎝ ⎠
16 7 i+ 2 j 3 3
~ ~
53
OC = 53 B2
B1
11 i + 5 j − 4 i − 3 j
~ ~ ~ ~
17 90 , 123.69 ,270 ,303.69o
o o o
4 4

90o, 270o or 123.69o, 303.69o B3
cos x (3 cos x + 2 sin x) = 0 B2

3 cos 2x + 2 sin x cosx = 0 B1


18 (a) θ = 1.842 2 4
5α = 6.5 B1

(b) 23.025 2
1 2 B1
(5) (1.842) * (candidate’s θ from a)
2

19 60 3 3

x 3 2(5 − 3 x )1 ( −3) + (5 − 3 x) 2 3 x 2 B2

B1
2(5 − 3 x )( −3) or 3 x 2
20 10 3 3
⎛ 2 ⎞ ⎛ 2 ⎞
⎜ 3 − 2 ⎟ × 4 or ⎜ 3 − 2 ⎟× 4 B2
⎝ x ⎠ ⎝ 2 ⎠
dp 2
= 3− 2 B1
dr x
21 h=3 3 3

h h
– =7
[2(3) − 5] 3
[2(2) − 5]3 B2

3
⎡ ⎤
( with the correct l imit ) or [x ]3
h B1
⎢ 3⎥ 2
⎣ (2 x − 5) ⎦ 2
22 a) m=5 2 3

2m − 3 + 8 + m + 1 B1
=7
3

b) 21 1
23 1 3 3
or an equivalent single fraction
15

3 2 2
× × B2
6 5 6

3 2 2
or or B1
6 5 6


14 1 3
or 2.8
24(a) 5

24(b) 1.296 2

2 ⎛ 2⎞
7 × × ⎜1 − ⎟ or equivalent B1
5 ⎝ 5⎠

25 (a) 1.1 2 4
0.1357 B1

25(b) 61.2 2

70 − μ B1
= *1.1 (candidate’s k)
8

“END OF MARKING SCHEME”


SULIT
NAMA:. NO. ANGKA GILIRAN:

PEPERIKSAAN PERCUBAAN
NEGERTPERAK

SIJIL PELAJARAN MALAYSIA 2OO9 3472t1
ADDITIOIAL MATHEMATICS
Kertas I
Sept.
2 jam Dua jam

Paper I

Two hours

JANGAN BUKA KERTAS SOALAN Markah Markah
Soalan
INI SEHIIGGA DIBERI-IATIU Penuir Diperolehi
1 J
2 2
1. Tuliskan nama dan nombor kad pengenalan
3 a
J
anda pada ruangan yang disediaknn.
4 3
a
J J
7 Kertas soalan ini adalah dalam dtyibahasa.
6 3
I 4
3. Soalan dalam bahasa Inggeris mendahului
8 a
J
soalan yang sepadan dalam bahasa Malaysia. .|
9 L

10 5
Calon dibenarkan menjawab keseluruhan atau
11 J
sebahagian soalan sama ada dalam bahase
t2 3
Inggeris atau bahasa Malaysia.
13 a
J

t4 a
J
Calon dikehendaki membaca maklumat di
15 a
J
halaman belakang kertas soalan ini.
16 4
t7 4
18 4
t9 2
20 a
J

2l 4
)) a
J

23 4
24 .+
25 +
Jumlah 80
Kertas soalan ini mengandungi20 halaman bercet:,k.
3472/l
[Lihat sebelah
SULIT

SULIT 6 3472/1
For
Examiner 3
Answerall questions.
Use Jawab semuasoalan.

Diagram shows psaph thefunction
1 the of f(x)=lz-zxl ror ttredomain_3<x<4.
RajahI menunjukkan bagifungsi "f(x) = - Zxl untukdomain-3 <
graf < x 4.
i3

Diagram I
State Rujah 1
Nyataknn

(a) the value of i,
nilai h,

(b) range of flx) correspondingto the given domain.
julat flx) berdasarknn domain yang diberi.

[3 marl<s)
13 markahl

Answer / Jawaoan : (a) h :

(r)
3472/l
SULIT

SULIT 7 34721r
For
U' a
a
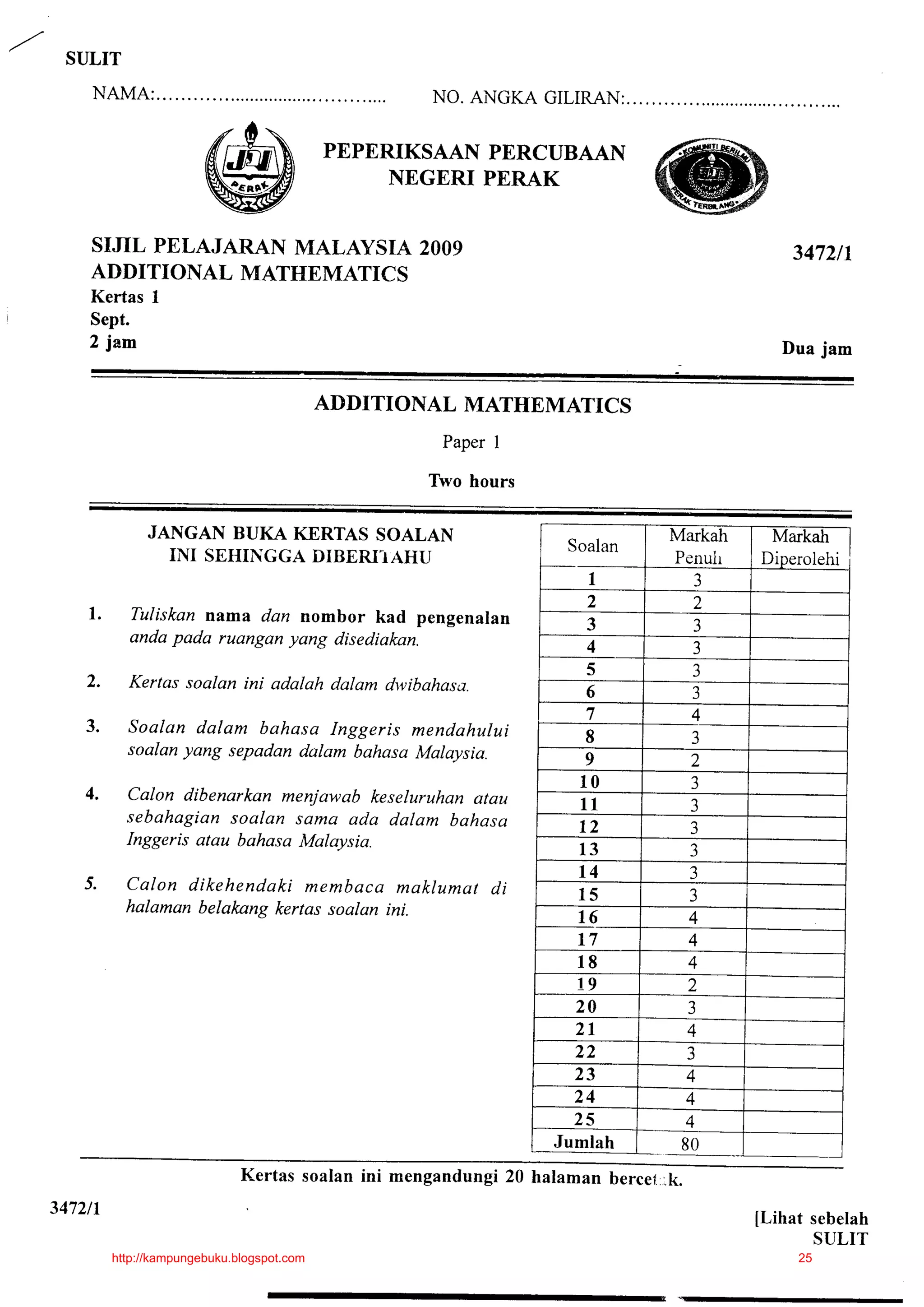
Given the function g : x - + If g(1) =:- , find the valueof 2 Examiner's
12marl<sl Use
__3 z
^
1
Diberi fungsi s : x -+ Jika g( 1) = 1, car i nilai ) , 12markahl
k z

Answer I Jawapan : )" :

-5
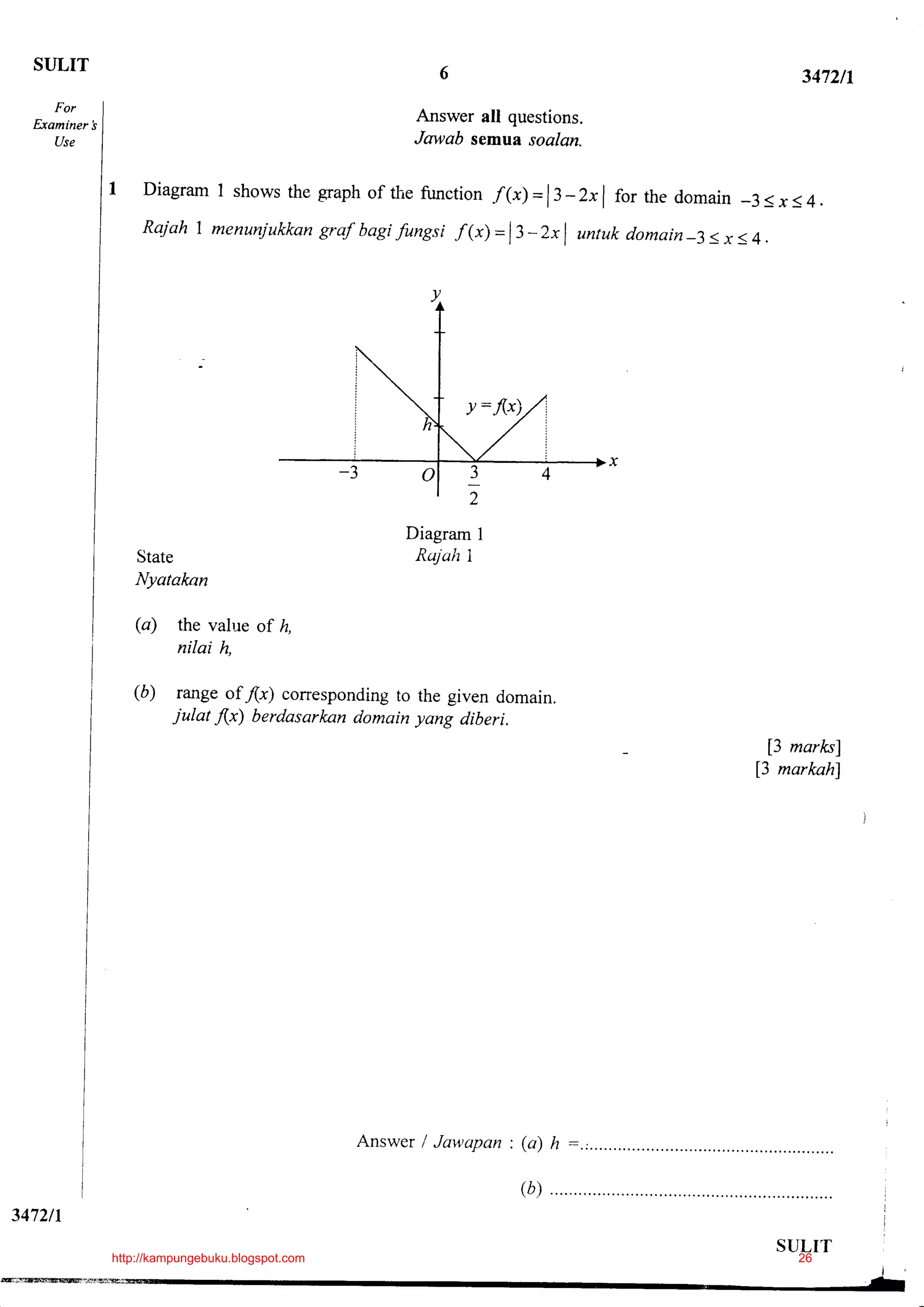
function-fg@)=3x2 and function 8(x) = 2- *2 ,
Giventhe composite
findl-4). [3 ntarks]
Diberifungsi gubahanf|(x) =3x2 -5 danfungsi g(x) = 2- x2, ceri A-4).
y3 markahl

Write the quadraticequation 2x2 -4x=3x2 +7x-15 in generalform. Then, solve it by
using formula. Give your answer correct to 3 decimal places.
[3 marl<s]
Tulis persqmadn kuadratik 2x2 -4x=3x2 +7x-75 dalam bentuk am. Seterusnya,
selesaikan dengan menggunakan rumus. Berikan jawapan tepat kepada 3 tempat
perpuluhan.
[3 markah]

Answer I Jawapan
3472/l [Lihat sebeiah
SULIT

SULIT 8 3472t1
For
Examiner's Find the rangeof valuesof a if 2x2 -.r-15>0. [3 marks]
Use
Cari julat nilai x, jika 2x2 - x - 15 > 0. [3 markah]

Answer / Jawapan

Find the coordinates the maximum point cf the quadraticequation !=4x-r2
of -9 by
using the method of completing the square. [3 marks)
Cari koordinqt titik maksimum bagi persamaan kuadrctik !:4x - 12 -9 dengan
menggttnakanknedahpen))empurnaan kua,sadua. 13 markohl

Answer I Jowapan :

It is given that Io g zs +2 l o g 5 Q 1, expr ess in ter m s q.
p = p of 14marks)
p+2log5Q=7, ungkapkan dolamsebutan
Diberi bahawa logzs p q. [4 markah]

3472t1
SULIT

SULIT 9 3472t1
For
)
8 x 2'-3 Examiner
b
Solvethe equation -3
1
[3 marks] Use
22n

r = t.
persamssn
setesaiknn [3 markah]
:r'=lt
L

Answer/iawapan:n:

It is given that the first four terms of an arithmetic progressionare 3, -8, x and -30.
Diberi buhswa empat sebutanpertama suatujanjang aritmetik ialah 3, -8, x dan -30.
Find the value of x. [2 marks]
Cari nilai x. 12markahl

Answer / Jawapan

l0 The third term of a geometric progressionis 16 and its common ratio is '

Find the sum to infinity of the progression. 13marksl
Sebutan kztiga suatu janjang geometri ialah 16 dan nisbah sepunya ialah

Cari hasil tambah hingga ketakterhinggaanjanjang itu. [3 markah]

Answer I Jawapan
3472t1 [Lihat sebelah
SULIT

I SULIT

Solvethe equation
8 x 2n-3
22n
-3 1. [3 marksl
3472t1
For
Examiner 3
Use

8 x 2n-3
persamaan--Fr=3-
Selesaikan I
l .
13 markahl

Answerliowapan:n:

It is given that the first four terms of an arithmetic progressionare 3, -8, x and-30.
Diberi buhowa empat sebutan pertama suatu janjang aritmetik ialah 3, -8, x dan-30.
Find the value of x. 12marksl
Cari nilai x. 12marknh)

Answer/Jawaoan:x:

10 The third term of a geometric progressionis 16 and its common ratio is '

Find the sum to infinity of the progression. [3 marks]
2
Sebutan ketiga suatu janjang geometri ialah 16 dan nisbah sepunya ialah ; .
J

Cari hasil tambah hingga ketakterhinggaanjanjang itu. 13marknhl

Answer I Jawapan
SULIT

SULIT 10 3472tr
For 1l The first four termsof an arithmeticprogression -7, -3, l, 5.
are
Examinerb
Use
Empatsebutan pertamasuatujanjang aritmetikadalah -7, -3, l, 5.
Find
Cari
(a) the fifth term of the progression,
sebutankelimajanjang itu,
(b) the sum of next 24 termsafter the fourth term.
hasil tambah24 sebutanberikutnyaselepas sebutankeempat.
[3 marks]
[3 marlcah]

AnswerlJawapan:(a)

(D)

The points P(2a,a), Q(b,c) and R(2b,3c)areon a straightline.
p dividesPR in the ratio 3 : 4.
Titik-titikP(2a,a), Q(b,c) dan R(2b,3c)terletak
pada satugaris lurus.
Q membahagi dengannisbah 3 : 4.
PR
Express in termsof c.
6 [3 marks]
Ungkapkan dalam sebutanc.
b 13markahl

Answer I Jawapan
3472/l
SULIT

SULIT 1l 3412tr
For
13 The variables and y arerelatedby the equation/=2x2 +4x3. A straightline graphis
x Examiner b
Use
obtainedby plotting { against x, as shown in Diagram2.
xo

Pembolehubah x dan y dihubungkan
oleh persamoan!=2x2 +4x3.Graf garis lurus

diperolehdenganmemplotka" + mebwan x, sepertiditunjukkanpada Rajah 2.
x-

Diagram2
Rajah 2
Find the value of m and n.
13marlul
Cari niloi m dan n.
[3 markah)

3472/l [Lihat sebelah
SULIT

SULIT t2 3472t1
For
Examiner b
14 Diagram shows straightline pe with the equation- -+
x v
?= |
Use
3 a

Rajah 3 menunjukkan x y r
garis lurus Pe yang mempunyai
persamaan - - = I
3 4
The point P lies on x-axis and the point e lies on the y-axis.
Titik P terletakpada paksi-x dan titik e terletakpada paksi-y.

Diagram 3
Rajah 3
Find the equation of the straight line perpendicularto PQ and passing through the point p.

[3 mark^s]
Carikan persamaan garis lurus yang berserenjongdengan PQ dan melalui titik p.
13 markohl

Answer I Jawapan :
3472t1
SULIT

I

, SULIT 13 347211

15 For
Examiner's
Use
a D
Jh A

B a

Diagram 4
Rajah 4

Diagram4 shows vectors OA'=g, OB'=b. OC'and Cd on a grid of equal squares.
Rajah4 menunjukknn
vehord= g, O?= b, O? aordi di atassatqhgrid segiempat
sama.

Expressin terms oi q and b.
Ungkapknndalam sebutan g dan 12.

---
(a) OC,

[3 marks]
13 markahl

SULIT

SULIT t4 3472t1
t - o r l 1 6 Diagram 5 shows a trapezium P?RS.
Examiner I
s
(Jse I Rajah 5 menunjukkansebuah trapezium PQRS,

I
Diagram 5
Rajah5
G i v e nth a tth e ve cto V d =@+4) L+ 6 j undTR) =3m i+ 107.Find
r

D i b e r ive kto rP Q=@+4 )t_ +6j dan SR' = 3m i+ 10 Car i
j.

(a) the valueof rz,
nilai m,

(b) the magnitude ur"ro, V/.
of
)
mognitud bagi vehor PQ'.

[4 marl<sl
[4 markah]

Answer I Jawapan : (a)

(b)

S o l v et h e e q u a t i o n s e c ' x - 5 = t a n x f o r 0 o ( x < 3 6 0 . .
3
[4 marl<s]
S e l e s a i k np e r s a m c a n3 s e k 2 x - 5 = t a n x b a g i 0 o ( x < 3 6 0 o .
n
14 markahl

Answer I Jawaoan :
3472/l
SULIT

SULIT 15 3472tr
18 Diagram6 showstwo concentriccircles with centreO. For
Examiner
b
Rajah 6 menunjukkan
dua bulatan denganO sebagai pusatnya.. Use

Diagram 6
Rajah 6

Given that OP : 6 cm, OQ : 3OB and ISOR= 50o. POR and SOQ are straight lines.
Diberi bahawa OP : 6 cm, OQ : 3OB dan ISOR = 50o. POR dan SOQ adalah garis
lurus.

(a) Find the value of 0, in radians.(Use z =3.142)
Cari nilai 0, dalam radian, (Guna n =3.142)
(b) Calculatethe area of the shadedregion.
Hitungkan luas kawasan berlorek.
14marksl
14markahl

Answer/Jawapan:(a)e:

The curve y= -f(x) is such that I x -2px-3,
' d wherep is aconstant.

The gradientof curve at x= 4 is -p. Find the value ofp. [2 marl<sl
Suatu lengkung y= f(x) adalah dengan keadaan !=2pr-3, p ialah pemalar.
d-r
Kecerunan lengkung itu di x = 4 ialah - p . Cari nilai p. 12marknhl

Answer I Jov,epan: p :.........
317211 [Lihat sebelah
http://kampungebuku.blogspot.com 36 S U L I T

SULIT t6 3472/l
For
Examiner
b 20 The curve ! = -2x2 +24x+r has a maximumpoint at x = /
Use ow h e r e r i s a c o n s t a n t .
Find the value of r.
[3 marl<s]
Lengkungr = -2x2 +24x + r mempunyai
titik maksimumpada x = r, dengankeadaan
r ialah pemalar Cari nilai r.
[3 markahl

Answer/Jawapan:r=

that Il, sfrXr = 5, find
Given

Diberifl,sftPr =5 , cari

r-l
(a)
J, sG)dx,

(b) [lr[rrra- rx]d-r
[4 marks)
[4 markah]

Ansrver I Jawapan : (a)

(b)
3472/1

http://kampungebuku.blogspot.com SULIT
37

I7 34721r
SULIT
of 6 and standarddeviation For
22 SetX consists 50 scores, for a gamewhich has a mean
of x, Examiner b
Use
of 4.5.
min 6 dan sisihanpiowai
Set mengandungi skor,x, bagi suatupermainandengan
X 50
4.5.
Calculate
Hitungkan

(a) the sum of the scores,Ix'
jumlah skon 2x ,

(b) the sum of the squarss of the "o"', It2

hasil tambah kuasa dua skor Lx2 '
l-3marksl
13markah)

a quiz' The membersof the
A committeeof 4 studentsis to be formed to organise
5 girls' Find the number of
committeewill be chosenfrom a group of 6 boys and
of
committees that can be formed such that the committee consists
untuk menganjurknn suatu kuiz'
Satu.iawatankuasadengan 4 orang pelqiar harus dibentuk
kumpulan 6 pelajar lelaki dan 5
Ahli-ahli jawatankuori it, aknn dipilii daripada satu
dibentukjika jawatankuasa
pelajar perempuon. Carikan bilangan jawatankuasa yang boleh
tersebutmengandungi
(a) 3 girls,
3 pelaiar Peremquan,
(b) at least2 boYs.
sekurang-kurangnya pelajar lelaki'
2
14marl<sl
14markah)

Answer I JawaPan :

[Lihat sebelah
34721r SULIT

SULIT 18 3472/l
For 24 '40Yoof the carson the road in Malaysia Malaysian
are made.'
Examiner
b '40%odaripada kereta-kereta jalan raya di Malaysia adalah buatanMalaysia.'
Use di

(a) If l0 cars are chosenat random,find the probabilitythat exactly 7 of them
are Malaysianmade.
Jikn l0 buah keretadi pilih secorqrawek, cari kebarangkalian bahawa
tepat 7 daripadanyaadalah buatanMalaysia-

(b) If n carsare chosen ranCom, probabilitythat all the n carsare
at the

Malaysianmade i, * . Find the value of n.
olJ
Jika n buah kereta dipilih secara rawak, kebarangkalian bahawa setnua n

buah keretaitu atlalaltbuatanMalaysia
ialah . cari nirai n.
#
[4 marks]
[4 markah]

AnswerlJawapan:(a)

(b)n=
3472/l
STJLIT

, SULIT 19 347211
For
25 X is a continuous random variable of a normal distribution with mean, p a&d standard
Examiner
b
deviation 4.2. Use
X ialah pemboleh ubah rawak selanjar bagi suatu taburan normal dengan min, p dan
sisihan piawai 4.2.
Find
Cari
(a) the value of p if the z-score is 2.2 when X = 18.4,
nilai 1t jika skor-z ialah 2.2 apabila X : 18.4,

(b) P(10.02<x<12.2).
14marks)
[4 markah]

END OF QUESTION PAPER
KERTAS SOAILIN TAMAT
SULIT

| ' .
I P+eriksaanPcrcubaan
SPM 347211
I NeseriPerak2009

MARK SCHEMEFORPAPERI ADDITIONAL L,TATIIEMATICS

Question and Marks
Working scheme Mark
No. allocation
1. (a) 3 I

(b) 0</(x)s9 or 9>/(x)>0
81: whenf(x)<9 or 0 < /(x) seen.

) ,)
9

ZtL J
BI
)"+3 2
3. _iJ -]

82: flx):l-3x
Bl: f(2-x27=3v2-5 or g '(x)=lz-x

4. x = 1.227 , - 12.23 12.227) [Both conect]
(- j

r-:-
- ^ . -__------------ 0-x - i s )
-ili{r1z -4
tszt 1_- [For substitutingthe valuesconectly
2(r)
-
into ttre formula]

B l : . r 2+ 1 l x - 1 5 = 0

3-
x<-| or x)3 conect]
fBothinequalities

vath '*re x 'raluesshcwn or ind.iceted.
82: The correct sectionis shaded

Bl: (2x+5)(x-3)>0

6. -s)
(2, 3

R 2 :y = - ( r - 2 ) ' - 5

L,
t't: 1,-lxz -4x+(1)z -(-2)21-9 or y = - l x z - 4 x + 4 - 4 + 9

1 l

34'12/l
SPM
Percubaan
Peoeriksaan
NegeriPerak2009

,<
8 3 : l o g 5P = tocsA) or

B2 : log5 p + lcg5 qa =log s52
logsP
o' . or los{ 5
2 - -

J

B'2:.-n+3=0
-20
91 . 23+n-3-2n+3
-19
-30-x -x- (-8) or -30-x =-8-3 cr
Bl : x- (-8) = -8-3 or
otherequivalentform

108
36
S* )
3

i 87 va:36
I
{a) 9
(b) 1320

B 1 , r , , = 2 ] L r { s )* ( 2 4 - l ) 4 1 o r

sx - s+=|Of-rl * <r8 lL2eT+(4-1)41
-r)4-
l:D
.t
'l b=-4c

82:b=8a

I -m:4,n=6

82:18=2+4(m) n:2+4(l)

Bl:1=2+4x Y=2+4X

2 - (j'-


SPM
Percubaan
Peperiksaan 3472tr
Negoi Perak2009

3 9
- =--X--
V 4 4

3' -.r 9
B2: v -0 = -:lx - (-3)| or c=---:
4 ' 4

4
Bl:. m.> -=-l
x
J

(a) 3s+!

(b) e-3b
Rl : g+3BO or q+(4CE)

(a) m= 5
*
r r 2m + 4 = i m ' ( i )
.
l(*.+)=im
w: t =| o, t"=J
(6) .fi7 or 3Jil or 10.82or 10.817 lr
x= 45o,i46.31',225",326.31"or 45",l45ol9',225",326o19'
x = 45o 146.31o oi x=45'and 146o19'
aiid
{3tant+2xtanx-1)=0
3tarfx-tanx -2:0
(a) 2.269

(b) 72.62 72.615 or
ot 72.61 72.608
or

-
rr2,zl:@' Q.26, (2:?5e)] equivarent
"r
ta)'

I
e=3
Blt-P=2P141-3

r=6
B,2:0=4r+24
9 11 9 = - 4 x + 2 4
dx


34't2/l
PeDeriksaanPercubaanSPM
Ne;eri Perak2009

(a) -s

(b) -2
f )1 ? |
B'2,to-l;-;) :

3x2
81 : 2x5 o, -,

(a) I x = 3 0 0 I

J
(5) Y 1 2 = 2 8 1 2 . 5
L.
i
t'-2 Zx' -36=zo.zs
B 1 : ^lLl-_ze=q.s
I

I ) U
50 t
i

(a) 60
sqx6q or 10x6 .
B!:
I

(b) 26s
t c r + u c r t t c r + u c oo r
Bi : uqr
I
I

1 5 x 1 0 + 2 0 x 5 + 1 5o r 150+100+15 f

(a) 0.04217
l

/?t/1'
B t : ' o C , l: l I ; I o r e q u i v a l e n t
I'
!,

)/ )/ F
it
(b) n=a
'!
ii
/au rta u
Bl :l: | == o re q u i v a t e n t ,l
5/ 625 d
5

J
(a) p =9.16 :l
1
-l
:l
:I
at . 1't -18'4- P
t a
l
'I
'+.L I

l
(b) 0.1842
1

16<z sYl!!!
r ) r . o(lWi:J
,,, , t r . . t 4.2 )
''-
:l
P(0.204s<70.?238)
<
l

4 .ll-

Panduan Lengkap
e-Book KERTAS SOALAN RAMALAN MATEMATIK SPM 2010

“Rahsia Pelajar-Pelajar Cemerlang MATEMATIK Terbongkar”

e-Book KERTAS SOALAN RAMALAN MATEMATIK SPM mengandungi

• 2 set soalan ramalan beserta skema jawapan

• 8 set soalan soalan percubaan negeri 2009 beserta skema jawapan

• Soalan ramalan 13 matapelajaran SPM 2009 beserta skema jawapan

• 5 set soalan tahun-tahun lepas 2005-2009 beserta skema jawapan

Cuma RM20.00 sahaja

Untuk keterangan lanjut dan tempahan sila layari

http://exam2010.gourl.org

Panduan Lengkap
e-Book KERTAS SOALAN RAMALAN MATEMATIK TAMBAHAN 2010

e-Book KERTAS SOALAN RAMALAN MATEMATIK TAMBAHAN SPM
mengandungi:

1. 2 set soalan ramalan beserta skema jawapan

2. 8 set soalan soalan percubaan negeri 2009 beserta skema jawapan

3. Soalan ramalan 13 matapelajaran SPM 2009 beserta skema jawapan

4. 5 set soalan tahun-tahun lepas 2005-2009 beserta skema jawapan

Cuma RM20.00 sahaja

Untuk keterangan lanjut serta tempahan sila layari


Lv

3 ; l ?l / l O. K,D PENGEI{,LAN
l l a ,c m a t i k
'flmoahan
Kertas I ANCKA GII-IR,
2009 nrO
Septembcr +
2 janr
JABATAN PBLAJARAN SELANGOR.

PROCTTANIPENINGKATANPRESl'ASI
SAINS DAN bIATtrMATiK 2OO9

Kod Pemeriksa
N! A'l'ltDl A'I'l K'L,lr! BAFLdN
Kei'tas I Soalan lVlarkah Markah
Penuh Dipcrolrh
L)ua Jam 3
2 4
J;)iCAll BIIi(A K[]iT/S S0'l,AN 3 3
iiii lijlilttiCC; Dlll ltl:i1"tAI {lJ 4 2
5 3
6 3
i. Ti:!i.sicta nc:rbcr i,iad pcngr:;ir!an,
7 3
ln;;ll:: gllir*n, n]jfir:rc/,:#; tillil<:t:zn
antll p t :!ctr: i.i :! t:!.t tGnq d :sJ{!i e k{t;i.
t1 it .]
9 2
.1-.
Kcrlcs so,-tiunini t:tlalct.tdaii;tt IO 1

dri!.,c1,,:.trt. tl 2
12 ..t
I ' / " ; . l t ! : ; ; tl , t l : , : ; . t , t . - .
l ,, l3 4
t,t iIJL:It.t!|tisooIJ/;,vaflg :tcl)t't,:|| (!aidn
bu!:. tst l'!,:Ia,.,u- l.l 3
l5 2
' : .: ,. . 1 . . , . , . t , . .- . - . . . . - . - . . , . . . r .
:j'.i,,/
,,r . ..'ir., t r s , , ( . ; , / t : ; < - , ' . . r 'rr , r . : r ;
, fi 3
..!it1Lt (t!|li lLi!.1m l:ctIu.sct l::ggt't i,'; ttlit:t .1
18
!:t i : t.t t t ]i.' ! c.,t t.
t
l9 3
5. Ct:iot t! ikt'itr.t<tnkin'.';itbt:ttt 2n .!
ontttl;t t!i htLi;nlLn b':Ilka;:i; i;<'rius 2l
1) 3
),3 4
21 -i
l) tl

J u l l'rl:]h

1 . " ' : r t ris i i m c n : : l r d L : a , t i l l h r l l r : : r n L r c i c c t : iC:r l I h : t l : l : i u n i Cr k ' o l r c c l ; , 1 ; .
i ? l l

i i,ii:::i r:::i::l:r1r
? i;.?,t1 :; i_rl,I
i

http://kampungebuku.blogspot.com www.banksoalanspm.com 46

s ut,tl' 3'472i1

T h e 1 b i 1 w r n g i l : r n : u h er n l , b c l ; ; l p f u l i n , n s * e r i n gt h e q u c s t i o n sT h e s ; ; m b o l s l . n a r c
' . g
lhc onescomn.:only used.

herikut boleh membctntuandu mt:njawah soalctn. Simbol-sinbol -vangdiberi
RLtrrtus-ntmus
aduluh yang bidsa digunakan.

ALGEBR.,
-br{i 4* lo:t . b
I g rog"b=,-
ld I Og. .J
2 9 T,: a + (.n l)d

3 A - A - A

l0 J,,= -l la+ln t)dl
4 2 '

5 1og, mn : log. rrt i log" n ll T,: ctr"
I

6 , m- 12 -l)
lu& roR,r, rog.,
n " , a(r" , at-r )
n
l-r
7 log, m"'., n la9um ll , . u
, ) ,= ; rl- I
l r

{i 1,1-c[1],cjs I i:,t !,:i;.j.t., J;
I

tl; dv r!,.; ,1 .,.;:r,..rili:r;r cLii..rc
rlr ar l.:: !,t: :,,: d i i' <:., h ! e:ig.l.y,1t
vt

!-
-: l,) . . ^- l^r.'.,
citt {;i'
2 v t l :
,, ,ly - -crit-..--....c:.n
'
v' ,!:t h
t ,
J '

: ./.il',,,.. 3,:iu-':ateii !.siptuiujai:;c;t
I
it, -
dit d;r
-1., -:- "
w -.---
3 ck rl;i d.,; f r
I ir,- '/: ()i ( {r/-.lJ)
'i,
J

Ir r ' (t)
J .

3.:72/l SUi,IT

www.banksoalanspm.com

ST,I,IT 3172t1

S1',TiiJ'l'iC:; I S i.4 IIST I X

,.Twr
'
- u"
./- '
- Lfx
'
)-l (n-r)l

nl
'-2 -
L " -
n r)!r!

- r': l0 P(AIB) = P(A) + P(B) - P(Ar8)
> f ll P ( X : r ) : n C , p r q 4 - ' ,p + q : 1

/ t 2 Mcan / Min , p: np
m :t + l = Y - 4 l c
f . , ) IJ
o = ^["ps

a.
,:.r-x 100
l1 v - lt
/:
Q,,

C,"tOivlE-I;iV / 6 ?.8':ii,L-triTJ

I Dlsl::rce/ -/rr.";;i,r 4 A:ea ol trter';eI Lucs sryiiigl
: 'l('r, - x,)' + 0z - Yt)' : I r:t, t--r.y.'i' -r.y,) - (;r. + ;r.,y,r- .r,y,
t 1, )j
r)(

I l )
i.'r ti.i /

r , , , 1 , : f r2t , . i i):) r
, 2 " ri +_yj
1 2 2
'; J I

J A poini rliviriial3a sr,-g;ncitt line o1'a
Ti l i k yt : ;1 *: en!; d: c,: i .s a tu t eii:b cre ng,tll r is
u
(''," "" tt,- '::t,
- - . - )l
'
t:ttrt tltln ,1

ll ii:::l r;l: il: I
.rti2li
: s r"i
{-t;'


5UT-tT' i172il

TRIGO' Ot1U' i,l I TRIGA"O.vE
IRt

Arc length, : r 0
.s sin (.4 L|9) - sin,.:lcos B I cos.,l sin B

Panjanglengkok,
s:j 0 sin (l + B) : sin -.1kos B I kos I sin I

._ -L
Arcf, ol sector. I = r-
c o s( l 1 A ) : c o s l c o s - BT s r n , 1s i n B
t ^
L:
Luas,sektor, e kos (l + B) = kos.,l kos B T sin I sin B
; i'

s i n 2, 1+ . o . 2 l : 1 t0 1an(l+B)= a n A + t a nl j
sitt2A + kcs2 I -"1
I + lfn /4 te;l 1J

l l
tln2 A:
, . " 2 . 1: l u r r n 2 A
I - tan2 ,1
, " k 2 1 : l ' + - t " , r 2I

anr".2l - l+ coi2l 12.
srn-,1 sin rf sin C
kosi:k2l -. I + kott/

:;in ?"1: ) si;rl ccs l I.l , , t , . .i,t 2 + c 2 . 2 l l r ' c o s , , 1
sin 2l ?-sil I kos I
, r 2 .- h? ', ,) 2bt l:ot I

sc:;2.':l ,:,,:,t ,1 ::":,'
- 2. cost ,4 |
-., I 2|r'12 I

:
ki:s 2.,1 kt;s2 -,'1 sirr2 .,1
: 2 k o s 2 , , 1i
== | 2 st.t't I

317 i1
2 SLLIT

I

sul.t'I 11 3172t1

Anslve r all qucjtitlns.
J uuu h sctr'ltJasrxt lun.

I :
.l(-t) r-l-rJ, iir thedornain 2!.ri
Gir cn thefunction l'

Diheri.limgsi = 11
fl.t) -3.q, untukdomuin 2 5x< I'

(rz) sketchthc graph ofthe function./(-t) the axcs in the answerspace,
on
l akLt
rktn graf untuk.fungsi flr) pttda pakt i-pttk i da ktm ntat:i;,m.iawapan,

(6) statethe rangeof/(-t) corresponding thc given domain.
to [3 marks)
nyatu*tn julat flx) berdusurkan domain yang diberi. 13narkah)

Answcr / Jawopan :
(") (b)

t
Ci;rn tlrc lr:nction:;./ (") = 3, - 2 ord ir{,r)'=/i:r - 3, 1l;:d
iliiti:r! f;irg::i ./ '('r) - 3,t- z dat: 2;i1' lt; 3, cari

(.n) /(;r),
,,,t tt t l-. 7. i"i,'::-/,t"

I-L *. ..i I.t

|.:: tsttr I .ltto1;ct:t : (t;)

(i)

| 1 - " -1 l I : - - l l . , 1
].11
:1,i7 SlrLi'f


3172.'l

Diagrarn shows
I thatreprtsents t'rnc:icn (-r)= ?-L,,
an:r :rv diagrarr the r/ * *.
:.Y-l
Rajah I menunjui&cn sualu gambtrajah antk panah vang mewakili.t'itng.si

Itx=lJ.x-m.
lr-l

,f x-p
x + 2 x- l

Dia;.;amI
Rcjoh 1

Find the valut cf
Cari nilai

a) m,

(b) p.
13mcrk;j
13narkchl

!,:-;.:,,:t: / ,!::',,;:".:.:;:t
. : (rN;:r --

(r))p'-

3:,12J1 5UI,IT


5 i,iLiT 31,12tl

F i n u t h c v l l u e o 1 ' f t i l ' r h c q i r a d : a t i c e q u a t i c n / r - r : . 1 . r + 3 = 0 h a s t l v ore q us .l
oot a
[2 marks]
Curi nilai h jiktr persdmdanquddrutic h.t? 4.r+3-0mempun.sui puncu-punc'a
!"ung sama. [2 markahl

Ans'wet / Jawcpun :

Fir:d thc range of valuesofp if ti:e gr:ph of tl:e quadraticidnctlon
JG).- "'-Zpx +2Jt +3 clcesnot intrrsectthe x-axis. f3 ncrk:l

Ccri juk:t niini p .jika graf .fing.si kuudratik ./(-r) = rt ' 2 px + 2 p + 3 titi;tlt bt:r:;i!ang
de;1qL:ri
lttr:tsr-r. 13 n:it:i;cltj

An:s';verI Ja',r't:1:::in:

l.il^* -.!. ^'- ",

: 1i1iN 5Ut_I'i


3 34121t
s 1,1.1-r

i;::ction 'r(r) = t it -')r' rvi.rcrc ald I
/r
6 Diegr-rm2 sl'ows thc gilph oiir r;Lratlratic
3rc conslSnls.
: ft (r + 5f ' tlengun keadcan
Rajah2 mattuniukkttngral bttgi /ungsikLratlrttik 1r)
h dun k iulutt Pcmular.

I
r
-f'

I' lgra:l 2
State 'tjeit 2
Ilyar, tt:
tk
(.r) thc vr.lue of ll,
niliii lt,
(b) oi'l',
thc valr.ic
nilti it,
tlc r:r-lu:ition fi:e:ui:; o! slj)li:lc y'
of 13n:arks)
(,J
p,.'r,;a:ntx:r Pt:ksi .sj;'tt't i'
! 13n::;rk.4)

r
.!iuLt
3.t"!21


Strl-IT 3112i1

7 l i o l i ' c i h e c q u a t i cr i :

St,I t:su i kun Stc rs a maun : 13marks)
1 l u c . ._ R t t3 markchl

Ans'Ner
/Jav,apan: x:

Given that logl -r1+ 5 logt-r : 2
Diberi logtxy t 5 log:x: 2.

lixpress.yin tcrr:rsof ,r. [3 mcrks)
y
Uxgkapkun cltlan sehuton
x. 13markahl

Ans',1..:/ ix.gc,r

Ii,ii:::rt::]11:.1:
2.+*l2ll SUL!?'


--

5U l- lT 1{) -t-l ,;/ I

3
( j i v e n t h c t i r r c cc o n s c c i i v c t c n n so f a g c t r l t t c l r ip r o g r c s i i o 'a r c 6 . a : ] d
c l
3
rvherex > 0.
Irind the value of-r. 12mark.sl
d
Diberi ligo sebuldn bertitrul-lurul dulum junjung gconrt'lri itiith 6, r and
3'
d e n g a nk c a d a u n r > 0 .
Cari nilui x. 12mcrkahl

A s,,n /.,/..rrtl, rrril : r :
cr

t0 Given the sccondtenn and th. tenth triL o i a n a i i l h n e t i cp r o g r e s s i oa r e 1 2 a n d5 2
n
rc pectively.

Diltcri bahcwt sebult:n ktditt t.lrutsebt; .tt l:t stp uli iI t .sttii tt j anj ctn ori tnrl i );
t g
iak:lt 12.d,-:i 52 .
nos!t;74-mttsir:g

Find
L.GfI

(l) tir: cori:n';cr"r
diiici'lrcr,
bztt sepu:yt,
(6) lire ltii;t tcr:n.
:;th||:{:ti perIul;0. li nurtu)

ri;r.. ; : (,,)
l',ils'l;t / .-/cr:

t))

34i2il ;cUtr,lT


_-

sul-t'r 1t) -ll;l/ l

fi
(iiven :l]c lirrceconsecrtivgtcr-]lns a qatilllclf progressitl'l 6. Nild
of ic arc
3
rvherex > 0.
F ind the valuc of -r. 12murlcsl
d
Diberi tigo seburdn bertitrut-lltntt &tlum lun jung l1conn'lri iriitth 6. r 'tntl
3
dengan keadaanx>0.
C.ari nilui s. 12markahl

A:'swcr/Jat'^apun:x:

t0 Given the sccondtenn ard t|e lenth trir ol-ar a;ilhmctic progression l2 and 52
are
rc pectively.

j
Diltcri bohawa schulr:n kt'tli:t dr:rts:abt.;:n l:cst'Jtt.t r .:;tttiltt onj ct;tgoritrutli);
liil
nic:;it;g-nos irg it:lch 12 Ci;:i 52.

Iiind
Cari
(l) conr.rl(.jn iiiilrrr,
1i.ie di
h:tt sei,tu:iu:,
(5) tire iil;t tcnn.
:rhuiutt perla;t;tt. ] r,l.:orks)

,.iilsi'r;t /.-/r.'r:o;:. ; : (,,')

t ])

il
3,1i2 Strt,lT


S t . I -l ' I rr 3112i1

II l,.is i 0 tcrms. (iivcn that thc lirst tcrrn is I an,.l lssttcrm
A gcorxc{ricprogrcssi!,n the
)
is 156, flnd thc conrnon ratio ol'this progrcssion. 12 nrark.sl

jttttjtmg gconrctri tttt,ttntrntui 10 .yehuttn. Dihti
Sutrttr sebtrturtpertrtnta iulah ! tlan
I

scbulan lt'rukhir ittlul:256, turi nishuh septnt;ubagi jujuktn int [2 markah)

At:..t;t, lJultcpan

i2 lJiagianr3 shous parl of a strf,ightlrnc grtp obtrined plotting agairst{
by -ry .
x
graf gtri. urtt.s
Rttjah 3 ntenunjuiiltun .sahaht:giun t,angdiperolchclengtnnempkst
xy
. 1
t:tclit:vtttt ; .
r irl,

(3, 6)
/"

t
l

lr:it::ii;;t -1
l!ult:it 3

trirprt:il; in ilrir,s ol -r.
y [4 r:rir,l;.]

U)1 k{tl *! n,l' .lu !{;rt,ycbit lt in .r.
! 1.1ntr.lith)

l : l } 1 : 15 ! : r : : : :
l . t ?- 1 i ; SII],IT

http://kampungebuku.blogspot.com www.banksoalanspm.com 57

SUI"I'I l2 3,r?:il

!3 Diagram 4 showsa strarghtiine ,'{B lvith the equation ] - f- - f .
-1 6
-Y _t
persamacn
Rajah 1 menunjukl<tngaris lurus AB yang mernpun;;ai
3 6

Diagram .i
Rojah 4

(a) Exprcssthc ccuatjon ofthe straightlire.,18 in grarlicntfonl.
Unglicpkan per.;,:;:itt:: gcri.slurus AB daian ltcntuk ltaceruntn.

(6) I.ind the cqn:-iloncf ttr: sir-:ii;;irt 1-';ri:cndicui:r l3 airCpr.ssing
lin; 1l thiough
the point B.

Curi perst;mtz::t i4:iri,s lt;r::,t 1clt itt:r.t!:renjir4! (1":t1!lr!n all:'lr
AB
nc!sl:ti titlli [. 14nrcrlisl
14nn;'!tal)

(j)

(i-,)

SU],IT


SU I-IT t3 3172i1

l.l Given that thc points l(1, 4), B(2h r l, 2) and ti(5,'1) arc coilinear,find the
value cf h. L3 mcsrks)

Diberi titik-titik (1, 1).8(2h+1,2)danC(5,4)ddalahsegari.s,carinilaih.
A
[3 markahl

15 cocrr"lintts p.
GivenOP= 7 i-.i andI'Q=9i+3 i, findti::: of

Diheri bdi:ava OF =l i- .i .l.r,ri! - 9 it-3j , c,trik,;ttrtlnt;t
Q. 12 matlrch)

[I,ii:: t r i.r;i:h
j,!"1
1.17 Ii iiLi'i


SLr t]'
t- l-l J1 ,:t I

l6 l)iarr:rnr 5 sho.rs a :r'ar)e;riLrnt
I'pr!.! *lrcr.,:fr(.)is parallcj to S,R.

Rafuh 5 ;nenunjukkn.yahtiu[r trap(.:itltn PQttS dcngan keltluun pO.selori dengun .SR.

J,r

P

l);,,-qral.lt
5
I :jtih 5

GivenFp-3.., Cri -2), 1t.'d),['O tl.
3
Dil'tri l,uit.r,t P() I r. ().: 2 r . , , i. ' ; " ) l.ti.

IlxL,rc"* '- teri:i:; of .r a::d 1 :

Un;;kepkn dilatn scll',tir;:t .r ditn ;'

(rr)

(r.) i':t.
|,1 ,,-.,-: ..

tl ,.^,l r,r

1r..,:i;ttf /,.1t|r.;;)a:ti :(c) :i.i'

(1,);rt

3.i72tl I;LI;,{T


sr;t_lT l-i 31't2il

li ( . i v c n t h a t t a n f ) - . , ' ? ,* h c r e I i s a c o n s t a na n d C " . 0 < 9 ! l ' ' .
t
Dibt'ri tan}- Ji , di.rrrn t tkth panrular t)oLz0"< 0 < 90".

F i n d .i n t e r m so f l :
Cari, clulant .chutan t.

( a ) c o t0 ,
kot0,

(r) s i n ( 1 8 0 "- 0 ) . [3 markl
13 n:ctrkahl

I
ti i:,,.r , ,
L l l I l ' , i .
- -r.
. . ] l :
I

3;11t1 ir'.1i,i r


l6 3412t1
SUI.IT

13 I)iaqrlrn 6 showsa scctr:rGP(] with ccnrreO
';ektor OFQ dengonpusat L)'
Rujih 6 mcnun;ukfutn vbuuh

lliagam 6
liuiah 6

: I radian,fiir,i
Given that OT - TP -.8 cnr, a:T I Q{.}I'
C

-- T'P -'U ctt:,t!t:': I {}C{': Lrar!icn' cari
Dibcri bnl:uwtt OT

(.t CP, in crn,
Oi', ttttldn cm,

(r) thc arcx, i;: c:rr, of l,'-: thir;:r-i i'iljl Ji' 14t:;critsl
'' /
! : : : . , ,d , : ! . : t t ( l , r ' . / . . . ' : ' ' r ' ' i i ' 14ncrkr:it)

(ri

(r)

5 l J - ! -1 1
3472i1


I
- t
-t
- sr.r.r'r ',1 3nzri
-
f l9 lrlo va, ia'lies,-r anC.1', relatedby the equalion.r'" .r(3 -r)r.
ue
I Civen that r increases a constant
at rate of4 units per sccottl, iind the ratc ofchang:
of-r whcn -r - 2. 13mark';l

Dua pcmbolehubah, r r)any, dihubungl<anr.tleh rutmoctn y = r(J r)r.
pe
Diberi y herlarnbah padu kadar malar I unit sesaat,cari fudar perubahun x
apabila r : 2. 13mcrkahl

.Lrt riet I .Jl',rapun:

Ii,ii r:t s':l;11:.or
3 " i?,tl 5iri,]-t'


ST'T,tT l3 t472i1

:0 The gradientfirnctionofa curve is p"t + 3, wherep is a constant.
The straightline
-- 5 2-r is a tangent to ihe curve at the point ( 2, I ).
"v

Fung.si kecentrutn lenglung ittLth px + 3, di nana p arlalah pemalar. Caris lurus
:
;, 5 - 2x ialah tcngen kepuda lenglotngpada titik ( 2, 1).

Find
Cari

(a) the value ofp,
nilai p,

(b) the equationofthe curve. [3mar,L,sl
J)?rsamaanlengkung iiu. 13markahl

,,'",ii ci I . l :;,".. t :;, t : I,t;)
trr; t

(I)J

3,fi2l1 I rii-lT


SUt,Tf it 3472t1

7l Givcn that | ---1- - a .=I, tln,l the ralue of k. 13marks)
'i (a .r)' 5
t n l
J
Dibtri | .1.,./r' , t a r i n i l , tA .
i 13markahl
'1('1 r)- 5

A set of dala rvhicll ccnsistsof l2 n:rni1-'ers a meanof rur
hes anr-l
l'arianceof 4.
Thr sun of tl:c ni::::bcrsis 360
Stii:t sel tlgla 1'cr:glcnliri dot ipath 12 notnbnr metnptutl,:rir;tin m dan yaricns 4.
I!c.;il t:t,,,ish br:;qironbor- nonLar iiu cC,slch 360.

Irir:'.i
(iti i

(l) tL:;;
v:iu:: ol'r;r,

(5) thc sLln of sr;urrrsolithi nulirbris. [3 r::i;l;11
!t:i:;i! tcn:i;t:lt bagi kt:a.'t:<!iianonl;or-itortbor ilu. 13n,arkr:i:l

lI iL+t r,1.,- lr

3 il2lx S i- !.{?'


SULTT 2ii

trophicsas prizeslbr a birdnliltlrll tournment.
A tea(ltcr wants to ch0ose5 dit.furi:nt
l wo t,ithe trophiesarc madeofpeu'ter and the otiier threeare nlade ofpiastic The
teachcrcan choosethe 5 trophiestiom 6 tlpes of pewlcr trcphiesand 8 1lpcs of
p i,lstiotrophies.

Seorang guru ingin nemilih 5 trttJi scbagai httdiah untuk suatu perlantlingctn
batlminton. Dua dar:pada troft adalah jenis pewter dun tigd )'ang lain adalahjenis
pla.;tik. Guruboleh memilih5 trof ittt daripada 6 jenis trof pewter danS jenis trof
plastik.

Find
Cari

(a) the number ofdifTerentways the teachcrcan choosethe trophies,
bilangcn cttra yt;ng herlainon grtnt ilu boleh ntemilih trofilro/i ilu,

(/') the ltumber ofways thc trophiescan be arralged in a row on a table if
the pewtcr trophicsmust be placcd llext to eachother.
bilongan sitsunan troii-tr"oJiilu boleh di:;usunclalamsualu bcris di atas meja

.jika lro/i-troJi pewtenne sli C!!cic'!tCi scbck:h-ntctyebeluh
14nar!<sl
14 markrih)

l":'-:;* l: / .,Icr'lr;irl,r: (a)

gtiL!T
3'i1211


SLI IT 2i l{7:,'!

21 ln a iurvey conducleC,:ncollegesrudents, is ibund thai 129,i, thc college
ir r.rf
studcn,sdo not own a computer.ln a san:pleof 10 collegesnrdenls chosenrandoml.l.
find

I)ulum :uatu soul selidik yang dijalankan ke atas pelar"t kolej, terdapat 12 9'o
pelajar
kolel :idak memptnfai komputer. Dalam saiu sutnpelyang terdiri daripadtt l0 orang
pelcltr kole.jyang dipilih secara rawuk, cari

(r.r) the probability that at leastone of them doesnot own a computer,

keburangkaI ian bahau.,a ekurang-kuntng sctu doripada mereka titluk
s
ntmpunyai komTtr!tr.

(b) the total nun:bcrofcollcgc students
who doesnot own a computerif the coilcge
has 1200 studcnts.

.junit:h pelajar kolej ycng tidak mempun.yuikcs:;puter
jika kotej itu terdiri
dariTudrt I 20t) orang 1t.l.lor.
14 narlcs)
11 mcrkahl

ll,il::t slLtir:i:
-a.f
i::.11 S U I-I'i


st. ..t-r :2 3472;1

25 Diasrrm 7 sho* s a standardnonnal distributiongraph.
R.;jah 7 nt' nunjukkan sun gritf iuhurun normal piatvci.

Diagram 7
Rajdr T

The probability represented the areaofthe shaded
by regicn is C 7416.
Kebarcngktliun yang diu;akili clah l:s:s }.,{tva:;cnberlorgk iclch 0.1416.

(o) Find thc valuc offt.
Ct:ri nilai k.

(6) rnnClnr vr::'i::l;l::
X is a coi'ltinuous nhich il n*rnally tl:11:i'r:utedilh a mi3r
u
j'1.
r-,
cf 85 :rnd a.slsda:d dcvi:r1-:;:n
Filil fir* vah:e c|Xrvl:.:r il'::z :co;,..is .. ( .

X iaLlr p:tni;o!el:i:h iitt:(:;'!:!ui}t'tiicl d::;t;;.:.,, ',:i;i'..i5
t r:',:t:',.:::!:,r:.1tr l;e;'!t:,i;t.t:'{:;;
dnit si:;li:'yt i,'!ttw:i 3.
gnrl 7711;;11;;:rlt;!u *.c,r-: i,tj,:i:
,)( ii. ['1 r;;;rlr]
':"
i4 r:''''

l.,f.i:-i r:]l- : jlil'.! l : i::11iilli;i
i i [.: i T.'l,li,.1.',.. ii ;'.,i: ;'..1!
i,r,..i

Jitztl


,' !,

S{,LIT t:i 3472t1

BLANK PAGE
H,'IL,IMAN }IOSONG


S i i . 1r ' 3172t1

I :i.-t)Rll.l'Io r {)R c.5DID.TES

i . T h i s q u t s t i o np a p e rc o n s i s t s f 2 5 q u e s t i o n s .
o

2. .,nswerall qucstions.
provided in this qucstionpaper.
3. Writc ,vouranswersin thc spaccs
'1. Shox your,'vorking.It nray help you to get marks.

5. I1-you wish to cirangeyoui answcr,crossout thc answerthat you haveCone.Then
write down the new aniiwcr.
'l'he
6. diagramsin the qucstionsprovided are not dra',vn scaleunlessstated.
to
'Ihe
7. marks allocatedfor eachqucstionare shownin blackcts.
i 8. A list of formulac is provided on pages2 to 4.
:
mathcnatical tlrblesaro allowed.
9. Fr.rur-figure
scienlificcalculator.
10. You may usc r non-piograntrnabie
I 1. LI3nd in this questionpilr,.i to the in.rigileiorat tlte end of the examination.

NiAKi,Ul,lr^'I' UNTI]i{ Cr'"i.(;iil

1. Fkrlus scctktn ini n,'ngati:!::;:11i 25 soalt;tr.

2. Jsv uh simul sacllil.

3. .Jgu'llsn uittto ht:irkkici: r.!!rt!i.spt;tlri niar:l )tc::g t! i.t,:t!iukr''t r.!ulum k:rics:;att!::t ini.

4. Tusijukksn lu; t;',keh-!t:t1].,';:t lr.j'::j:iE L:Jl'Yt l;::;ji: ir;:tt71itu r;:t:h. Itti I'tt!el; r:t:nbcttitt
lt
a n ltt t tt ! : rk r:tetl J: :;t i : :'fu ''t :i: tr'it,::lt.
';t,'ti.-;;t.i r!t'i:,.;::;t kc:t:t::; jo.+apr:n ri:itg tt!u!t
5. -tikt ntrlu hcnit!1 ntuit*c:.j,::,,":a:ltr.rs!,
dibu::t. Xenuditi1 l!t!;:; j 't',:ii;i:,t
r-(:n.: i':,':i:nt.

6. litju);1.r.:i'tg r;:tn,qiri::;1i sr.tui::rtti:!ti; dilirl:it ;i.ti',;;"::tI sku!t; l;:':u,;li clitt's !:;.itttt.

8. !'u!:.t :;cruirtLi tit :ii.t diskii!.!.1.r,t,:!i ijcrtfi:.tn ?, iit:.,11:: 4.
(). B:.iktt sil)r rtda,'rttiik tt,:i;::: rt.':g)it i!hrn,::ri;ut'.

iti:!:i;!!i!r
tiii;cttitrit:t't t,-tt:r;:.,,;i:i:':.1;i)1
IA. .,1nilLr s6:,tlif'l .t t:.'t;7tidu.L bo!tit r!t;;;o"1;r;;n.

12. S:rc!:kt;tt k!r:t1, so{rldtl in! lt,:;:,-;1,!ti
1.ttt:1:,r;',;'0,:; pitalt tl.:h;r ra;),..ril:c{r:1.
y)t'Stt'rii::;t;r;:t

2tl
-147 gJLIT


+
progrlnr per
ingkatan P r e s l a r i
'ltltti{s'!! !lq1!"nt,1t c r l l : r r kSla i n s l l : r r c n r r r t i1 0 0 9
t
& k
i I i g t.hcrr:e p:rpcr
I
r
]
(.1)
t(r_,1

I
as
-uraph sh,trvn
i

...shapcd
l ( n )n 5
'(t
)r t5
rl
l., I
''lr''rrrh I
----l---->
i.- i
I

(b) 0<.l lr) < 7

t

(h)k-i -)
2
I
l s
4k 3-j I B2
/'(2)=c lBz BI

9
I 1 " . 3

2 lo-1, -r6y iogr g B2
4-p B) Iog.,11- ' lo-g;rj logr 9 B]

I

4(rx3) 0
- B1

-l r., -l
/,4 I
(p -3)(p, t) o
I 7rr tl -5
(-2!,)t 4(2p l) (_)
tl 1 2n x i a


i i
l r ir . ?
t i

I
'
l5t,
()o ) ' l_i'i
,a 7. 5l: - f1 /(
BI
i 1,, l-;,

t
-
I I 3
.,
_r .- |
lLt) Rl' -. /l( ) + O/,

I z 1, -1r 2
.rl' i l
-Y
c - j
ttr- )t tjr./)1) BI
,t] l B2
BI (.b) Fi - .r: 2
-v
or ll,f BI

,rU j,
(.h)
! -l_ r:+ _l
2 2
1 ,
= (_r
-).' o -i) ,r
.1
2
l
2 s i n( 1 8 0 " 0 . r= s i n0

J
(a) ll3t/ri126

(r) l8 2l
(i

]lt+l I
lrttt:rr 'i;j I r xt r r
s D-)
2 )
I
J j t r 't ' ; 'fil
I
I


- I
19
l9 tlx a f. I,
I : :-t I (u) 8.10 2
I '8., ncr, oc,
.':^ ; ', I t BI
I i,7;'l'.
i i*-, i"'i (r) i8
'l', r .11
/ 4rlx2x I x2
7

B1

5
(u p--
l0 2 z.t o tzts
l { u ) "'c,,
I I 10l2f,1088;,,, BI
(6) ,r,..'lx: + 3-r+ 2 3
(r5)334
5 " R2
'1 ' - 4 - r - + - i - Y + a C . 2 75 x 1 2 0 0
3 B1
BI

1,)
2l J (t't k I 13 2

l 1 4 l l'(z) k) - 0.1292 BI
,1-k -) 5 I
B2
(,';) ,'..81.61 2
{ 8_5
'
It+ ..) ]* 3 BI
L ("i)1, BI

22 (.u) rn - l0

(D) i ud:18 z

)-rl
' - I
I l(, I
12 I -
l B l


l"

SULIT 3472tr
NAMA:

TINGKATAN:

.IABATAN PT),AJARAN TERENGGANU

PEPERIKSA"dNPERCUBA,{N SPM2OO9 347211
ADDITIONAL MATHBMATICS
Kertas1
Sept2009
Untuk Kewnaan Pemeriksa
2 iam
Markah Markah
Soalan
Penuh Diperoleh
2
JANGAN BUKAKERTAS SOALAN INI 2 J
')
SEHINGGA DIBNRITAHU 3
4 3
|. Tuli.t Nama dar Tingkatxn pada ruong,yong 5 3
disediakan. 6 3
2. Kertas soalan ini adalah dalatr dwibahasa 7 3
8 3
3. Soalandalam hahasaInggeris mendohuhti
soalan yang sepadandalam hahasa Melayt. 9 4
l0 2
4. Calon dibenarkannenjawab keseluruhan
atou sebahagiun soalan sama ada dalam I L 3
hahasaInggeris atau dalam bahasa Melayu.
l3 4
5. membaca
Calon dikehendaki maklumstdi l4 3
halamanbelakanskzrtas soalan ini' t) 3
l6
A

l8 2
l9 +
20 3
2l 4
22
LJ 3
24 4

I Di.!,ll kln ol(h;
AKIIAiI NEGERI TNR[N(;(;AN ti
25
Jumlah
3
80

l ) i h i a ] / ] io [ t h :
KNRA,'AAN NO(; ERI TI]RI]N(;(iA NtJ

Di etuk olch
P!rcetqkan ytJ'atu, lsln. Terenggunu Sln' Bhl.
lit|: 60Q-b66il6 |I 6(t-2 I6t)| f-ukt: 6t)Q-6(6 (t6 | l.00()l

. Kertassoalanini mengandungi halaman
24 bercetak'

347211 @2009TRIALwww.banksoalanspm.com
sPM HakciptaJabatan
Tefengganu
Negeri
Pelajaran [Lihrt sebelah
74
SULIT

SULIT 3472/l

Thefollowingformulaemaybehelpfulin answering questions. symbols
the The givenarethe
onescommonly used.
Rumus-runus berikut bolehmembantu
andamenjawob yang diberi
soalan.Simbol-simbol
atlalahyang biasadigunakan.

ALGABRA

-b! - 4sc los^
--=-:-b
l. .r = 8. log- D :
Iog. a

T, = a.tn'l)d
2. fxt={"^
ro.s, =
-t. {+d = {-' iza+tn-al
ll. T" = 1v'-l
({y = {'
a(r" * l)
5. log mn = log, m + log, n
J' *. I

o.
. m
lo& ._ =logE'..m-logltn r3. - fr, ,,t.'
.r-
7 . log, mn = n log, m

CALCULUS KALKULUS
/

l. y:w 4- Areaundera curve
Luas di bawah lengkung
dv dv . d- u
J' r,..
:
dx dx dx )Y dx or lalau
du dv
, v ..-- - u--' b
^ u a Y- , **7- d x
d x -
)x d.r'
v d,
5. Volumegenerated
- d -:- = ---:- d -- u
v d v
-J. x Isipadujanaan
dx du dx
b
= lfi v- fit or I alau

b
=
l|t x- dy

'fRlAt,

317211 A l(n9 Sl'M Hak Cipta .labltlrn Pcll.irurn Nclrcri lcrcngganu sut.IT
ILihat sebelah

ST]LIT 3 3172/l

STATISTICS / STATISTIK

-
l.
Yy
7, ' - - W . I{ /

Fr
N /,'i

Llx 'l!
8. = -

Lf n-r)l

i _, ,-'.=- ,1|

r o = , / n f i . L = f r : t ;1 ,
"r 7. L-' -
(r - r)l r!

t0. P(AvB)= P(A)+P(Bt-P(.4^B)
@mmmmmml=w;
I :r J:/ f l . P ( X = r ) = n C P ' q ' - ', P + q = |
,

l].v-r) l C 12. Mean Min = np
I
5 . m = L + |" -*
t f l
'/ l,r )
13. o =.,lnpq
n,!
E
6. y= v l[S
rlt ', - " r'
Qo

(GEOMETRY)
CEOMETRI

1. DistanceJaraL
I I tiga
4. Areaoftriangle Luassegi
it, , +xr}r) -(x?.vr xry, +r,y3)l
+
= - - x 2 ) 21 y 1 - ! 2 2
J1x, * l { " , - u ,* t r t ,

2. Midpoint Titiktengah
/
( x ,, + x' . v , + v .l
(r-ul= I - :r--,1-:I
l 1 1 t

3 . A pointdividing segment line
a ofa 6. i=
Titikyangnenbahagisuatutembereng
gans
(nx,+mx, nv, my,
+
=
(x.-Y) l- . - I
m+n m+n )

3472/1 A 2009 IRIAL SPM Ilak Cipta Jabal.rnPelaiaranNcgcri Terengganu
ILihat sebelah
http://kampungebuku.blogspot.com sul-tT 76

S]TJLIT 3472t1

TRTGONOMETRY/ TRIGONOMETRI

i. Arc length,s = rO 8. sin(l t.B) = siM cos8 * coM sin8

Panjanglengko( s -70 sin(,4 * A) = sinl kos.BJ kos,4sinj

2. Areaofsector = ! rz, 9. cos(l + B) = coMcos6 T siM sinj
z

! kos(l t B) = kos,ekos.BT siM sinB
Luassektor,f: i2g
2 '

3. s i n 2A + c o s 2 A : I tsnl t tanB
to. tan(l t B) =
I + tanltanB
s i n 2 , {+ k o s z r = r

11. tan2A = ,",u 1 ,
4. seczl = I + tan? A L*tan'A

sek2l - I + tan2,4
b.,- '
2. -!-=
srnl sinB sinC
5. cosec2l = I + cot2l

kosek2l = I + kor2l
1 3 .d : h"+c'-2bccosA

d = b2+t-2bckosA
6. sin 24 = zsiM cosl

sin 2,4 = 2 sinl koM
14. Area of triangle / lna.r se8i,iga

7. cos2l = coszl - sin2I = I aDsin C
2
= 2cosel-l

= l-2sin2l

kos 2l = kos2l * sin2I
= 2koszl-l
* I *2 sin2l

347211 A 2009 TRIAI- SPM Hak Clipn Jabatan
Negeri l'erenSganu
Pelajaran [Lihat sebelah
STILIT
77

SULIT 3472t1

For
Answer questions.
all Etamlner't
Use
Jawabsemuasoalan.

Diagram shows function/thatmaps to/ andthe function thatmapsyto z.
I the x g
Rajah I menunjukkanfungsif yang memetakan kepada danfungsig yang memetakan
x y
y kepadaz.

Diagram1
Rajah I

Determine
Tentuktn

(a) c '(6)
(b) d(4)
[2 narks]
12narkahl

AnswerlJawapan:(a) I

(b)
r-:
I l2l

{ l

347211 @ 2009 TRIAL SPM Hak Cipta JabatanPelajaran
NegeriTerengganu ll-ihat seb€lah
s't]I,xT
78

I*

ST]LIT 3472t1

For Thefunctions/and aredefined f: x --+I - 3x andg : x -t x2+ 3.
g by
FJarninet's
Use
fdan g ditatviJkanolehf : x -+ | - 3x tlan g: x -+ x2+ 3.
Fungsi-fungsi

Find I Cari

(a) d2}
(b) I'd2).
[3 marksl
[3 markahl

2
Answer Jawapan'.(a)
/

t;
Findtherange ofvaluesofp suchthaltheequation -, = p *2 hasno realroots.
Z*
12narl<sl
Cari julat nilai p dengankeadaan rsamaan - x = p - 2 tidak me
pe zxz mpunyaipunea
nydtd. [2 narkahl

3
r-:
I l2l

r--)
347211A 2009 ]'RIAI. SPM Hak Cipla Jabatan
Pelajaran Negeri Terengganu lLihat sebelah
sLlllT

Stn,IT 3472tr

4 equation ir + 8 = 0 is twicetheother.
Giventhatoneofthe rootsofthe quadratic x'* For
Findthe values ft.
of [3 marks] Exominer's
Use
Diberi bahawa satu daripada punca-punca persdmaan kuadratik t' - k + 8 = 0 adalah
dua kali ganda yang satu lagi. Cari nilai-nilai k. 13markahl

4

Answer/Jawapan:k=
T_:3 t
I t

Findtherange values /for (/-4) > l8-t.
of of [3 narles]
Carijulat nilai t bagi t(t*4) > 18-/. [3 markahl

5

G
1

3172/1 A 2009 TRIAL SpM Itak Cipla Jabrranpehiafan Negeri ltrcngganu
[Lihat sebelah
STJI,TT

I

$nlT 3472tr

For Diagram shows graphofa quadratic
6 the function/(x) = 9 - 2(x - l)2 andthe
Ftqmlner's maximum pointis (r, &),where and,t areconstants.
I
Use
Rajah6 menu4iukkan graffungsi kuadratikflxl = 9 -2O - h)2yang mempunydi ti,ik
malrsimum k), dengankeadaan dan k adalahpemalar.
(h, h

Diagram 6
Rojah6

State Nyataknn
I

(a) thevalueof*,
nilei k,
(b) thevalueofi,
nitai h,
(c) theequation the axisof symmetry.
of
persamaanpaksi simetfi,
13narksl
[1 martahl

Answer Jawapan: (s) ,t =
I

m
6
(b) h=

347U1 a 2009 TRIAL SPM Hak cipta Jabatan
NegeriTerengganu
Pelajsran [Lihat sebelah
STJLIT
81

ST]LIT
3472/r

7 Thevertices atrian are
of ele p(7;.3.), - --''- _t). Given thearea the
5)and n(,L
triangle 19unit2, thepossiblie(_1,oit.
is finl frlu".
that of For
Erominer's
[3 narksl Us
Bucy;buc.uslb.u7lysttigaialh gl_1,5) danR(k,_t). Diberibahawa
-' '- '- .ii
tuas
itu cart .l(7,3),
segitiga iatah t9 unit2, nilai-niiiliri ^ung*iiiogi
i. ^**on

I J
Answer I t3l
/Jawapan: k=

Sofve equarion
the Z't(Blb) = Jj .
{3 narksl
Selesatkan
persamaanZ7(g1b) - Jj .
13narkahl

I

Answer Jawapan:
I
r:l t 3 l
I

www.banksoalanspm.com llihat sebelah
1472/l A 2f[9 TRJAL SpM Hak Cipra Jabaran
pelaiaranNegeriTerengganu
St]I,TT

lo 3472t1

For Diagram9 showstwo sectorsOpP and0lt8 with centreO.
Iianiner's
Use Rajah9 menunjukkan sektar,OQPdan ORS,
dua berpusat
O.

Diagram 9
Rajah9

GiventhatOQ= 16cm andtheperimeter sector
of OOPis 42 cm.
Diberi bahawa = 16cm danperimeter
OQ sektor
OQPialah42 cm.

(a) Findthevalue d, in radians.
of
Cari nilai 0, dalam radian.

(6) If theratioO]t I RQ = 3 : I , find thearea sector
of ORS.
Jika nisbah : Rg = 3 : 1,cari luassektorORS.
OR
f4 narkr)
[4 narkah]

9
t--: 4 l
I t
Answer/Jawapan:(a) e =
(r)

www.banksoalanspm.com [Lihat sebelah
317211 A 2009 TRIAI, SPM llak Cipta JabatanPclajaranNcgcri Tcrcngganu
ST]LIT

SL]I.IT u 3472/r

10 Given three
the consecutive
ferms an arithmetic
of progre.ssion 1 2 , 3 k - 2 a n d 4 + k ,
are For
where is a constant.
* Find thevalue k.
of Erominer's
[2 narks] Llse
Diberitiga 'rebutan
berturatansuatu
ianiang arilhetih ialah rz,3k - 2 daa4 + t,d€..ga..
kesdaan adalahpemalar. Cari nilai k.
k
12markahl

l0
I --l
Answer / Jawapan : k - I
|
t - ll
|
?

11 The first threetermsof a geometric
progrcssion 36, 12,4.
are
Tiga .rebutan
pertama sudlujaniang geometriiqldh 36, lZ, 4.
Find I Cari
(a) the fourth term,
sebutankeempat,
(b) the sumto infinity,ofthe geometric progression.
hasil tambuh hingga sehutan ketakterhinggaan, bagi .ianjong itu.

[4 marks]
14markah

ll
Answer
lJawapun:(a)
t--:4 l
I l
(,5)

3472/l A 2009 TRlAt, SPM Hak Cipta Jabaran pclajaran Negcri Terenggallu
ILihat sebelah
http://kampungebuku.blogspot.com SLII,IT 84

I.

SIJLIT t2 3472t1

For
Examiner's
Use
Given h = ! a,ld/r 3q,
that = expr€ss'"r
r ofp q.
terms and
[+J'"
[3 marlcsl
t!aolam
Diberi bahawa = 3pdank= 3q ungkapka, - - t
h , n'rgr( sebutan danq.
p
e J
[3 markah]

t2
r-----]
t - J
I l ? l
Answer / Jqwaoan :

Giventhat logtQ.- logeP ' = -1, express in terms 0.
P of [4 narksl

Diberi bahawalogzQ- log eP 2 = -1, ungkapkan dalamsebutan
P Q. [4 markoh]

l3

T-;l4 l
I t
Answer / Jawapan :

347U1 @ 2009 TRIAL SPM Hak Cipta Jabatan
Pelajaran
NegeriTerengganu [Lihat sebelah
S]T]LIT
85

STJLIT t3 3472t1

l-or
Exaniner's
Use
14 Tablel4 showsmarksobtained a groupofstudents a monthlytest.
by in
markah
Jadual 14menunjukkan pelajar dalamsatuujian
yang diperolehsekumpulan
bulanan,

Marks l -20 2l -40 4l -60 6l - 80
Markah
Numberof students o 9 l3 t2
Bilanganpelaiar
Tabtel4
Jadual14

Withoutdrawinganogive,find thethirdquartile mark.
Tanpamelukisogif, cari markahhnrtil ketiga.
[3 narks]
13markahl

l4

t;

www.banksoalanspm.com lLihat sebelah
347211 A 2009 TRIAL SPM Hak Cipta JabatanPclaiaran
NegeriTerengganu
STJLIT

SL,'LIT t1 3472t1

E a iher's
Use 15 Giventhat theequation a curvewhichpasses
of throughpointP is y : 12r- I )2.
The normalgradient the curveat pointP is -;. Findthe coordinates
to ofP.
I
[3 marlcs]
Diberi bohawapersamaansuatu lengkungyang melalui titik,P ialah y = (2x * 112.
Kecerunan normal kepada lengkung itu pada titik P ialah *- . Cari koordinat P.

13narkthl

l5

tG

3472/l O 2009 TRIAL SPM tlak Cipta .tabatan pelaiaran Ncgeri Terengganu [Lihat sebelah
SUI,IT

S{JLIT t5 3472t1

l 6 Giventhat = 7, findthevalue
of
IS@a,
I
4
f
utDcrt bahawa = 7. car! nilui bagi
I RG) dx
I

I

(4) | .S(-r) .
dr

(D)- fI lls("r)- nl dx = 25.
z )""'

P l t K o Jl l' 2 ( x l -
" -
Dl dx - 25.
l

[4 marksl
[4 narkah]

Answer/Jrn,apon:(a) 16

( h )p : t__]l
I l4

a)

3172/l A 20{)9 TRIAL SpM Hak Cipra Jabardn pelaiaran Ncgcri Terengga u
Il,ihat sebelah
http://kampungebuku.blogspot.com SUI,IT
88

s'utxT lo 3472t1

For
Examiner's 17 A curvewhichhasgradient function - 2, where is a constant,
ftx I passes
through
Use
points l0) and(2, 0).
(0,
yang mempunyai
Satulengkung fungsi kccerunanla -2, dengankeadaan adalah
k
pemalar,melaluititik-titik(0, l0) dan(2,0),

Find / Cari

(a) thevalueof ft,
nilai k,
(6) theequation
ofthe curve.
persamaanlengkungitu.
14narlcsl
14narknhl

l7
T-:l 4 l
I
Answer/Jowapant(a)
k:

(b)

f47Al @ 2009 TRIAL SPM Hak Cipta JabatanPclajaran
Negeri Terengganu fl-ihat scbelah
http://kampungebuku.blogspot.com ST]LIT89

ST]LIT l7 3472t1

--t
For
18 Diagram 18 showssquaregrids where OP = a and OO = b. Exaniner's
-+ Use
Rajah 18 menunjukkangrid-grid segiempatsama dengan keadaan O P = a
--'
dan Og =6.

.tt

P
; l a
t

(,t
A
Diagram18
Rajah 18
-+
(a) Express in termsof a and b.
OR
-+
Ungkapkan OR dalam sebutan^ dqn b.
-+
(D) Intheanswer
space plot label point
given, and the Swhere
RS=b*2a.
Pada ruangjawapan, tanda dan labelkan titik S dengan keadaan RS = b - 2a.

[2 marksl
12marlcahl
-)
lJawapan:(a) O.ie
Answer =

(b)
R

1E
P

0
t-t l 2 l
I
a

o
A

347211A 2009 TRIAL SPM Hak Cipta JabatanPclajaranNegeriTerengganu ll,ihat sebelah
ST]I,IT

L

SUI,IT lll 3172t1

Fbr 19 Diagraml9 showsa parallelogram
PpR.S Mis the mid pointof Q,R.
and
E atniner's
Use Rajah 19 menunjukkan selari PQRSdan M ialah titik tengahQR.
segiempat

Diagraml9
Rajah 19
--t
Giventhat PQ=4i+ j and PM : 5i + 4j, whefei andj areunit vectors parallel x-axis
to
and y-a,xisrespectively.
-+ -+
Diberi bahawo PQ = 4i + i dan FM '= Ji + 4j, ctengan kzadoani dan j masing-masing
aclalah vektor unit selari denganpaksi-x dan paksi-y.

Find I Cari
-+
(a) QM in termsof i andj,
-)
QM dalam sebutani dan j,
-)
(b) (D tPst,
(ii) the unit vectorin the direction *
of .
veklor uni! dalam oroh 1S .
14marksl
[4 markah]

t9 -+
Answer Jawapan: (a) QM =
I
T; l 4 l
I (D)(i) lPsI =

r-)

3472/1 A 2009 TRIAL SPM Hak Cipra Juba(an I'elajaran Ncgcri Terengganu [Lihat sebelah
http://kampungebuku.blogspot.com SLLIT 91

SUI,IT t9 3172t1

line graphof log royagainst ro:r.
20 Diagram showsa straight
20 log Ilaminer's
Use
graJ'garislurus log rcy meluwanlog nx.
Rajah 20 menunjukkan

lo8ro
Y

(l l, q)

l0 *

Diagram20
Rejah20

calculate value
Civenthat-y= 1000x?, the ofp andof4.
Diberi hahav,a = 1000x2,
Jl niloi p dannilai 11.
hitungkan
13marksl
f3 markahl

z$
AnswerI Jawapan : p:
T-:l 3 l
I
"'

n

Pclajaran
347211 A 2009 TRlAt, SPM Hak Cipta Jabatan Negei Terengganu U,ihat sebelah
SULIT

20 3472t1

For
Eiquiner's equation 2x- 2sint=0 for 0" <x < 180o.
Solve trigonometric
the sin [4 marksl
Use
Selesaikan
persamaan
tligonomerri
sin2.r-2sinx=0 untuk SxS 180o. 14markahl
0o

2l
T_:4 l
I t

Theprobability Raihan,
for Michelle Amira qualify thefinalof a school
and to for level
'' I
publrc
speaKrngcontest -. 1 * a ! r e s D e c t i v e l v .
are
5 g
Kebarangkalian
bahawaRaihan,MichelledanAmira layak keperingkatakhir pertandingan
syarahanperingkatset<olah
adalahmasing-masing *"
*,i *
Cafculate probability / Hitungkan
the that kebarangkalian
bahawa
(a) onlyoneofthemwill qualify,
hanyaseorangdaripadamereka akanlayak,
(6) Raihan Michelle qualifo.
or will
Raihanatau Michelle akanlavak.
14marksl
14markahl

)',

T_:] l
I l4 Answer/Jawapan:(a)

t l (r)

pelajaranNegeriTerengganu
347211 A 2009 TRTAL SPM Hak Cipta Jabatan [Lihat sebelah
SULIT

SUI,IT 21 3472/l

Exsniner's

EMtrEtrHtr
Use

Diagram23
Rajah23

23 Diagram shows
23 five letters two digits.How manypossible
and wayscanall theletters
andthedigitsbearranged if
Rajah23 menunjukkan lima huruf dan duaangkt. Berapabanyakbilangancara ,semua
huruf dan angkndapatdisusunjika

(a) none ofthe letters digitsis repeated.
and
tiadl huruf dan angkadiulengi.

(b) thedigitsareseparated each
fiom other.
angku-angfuiadarahterpisah
antarasatusdmarain.
13marksl
[3 markah]

tl
Answer/Jawapan:(a)

(r)
l--J 3 l
I l

/

347211 A 2{X)9TRIAL SpM H.rk Ciptr Jabahn pelajarrDNegcri Terengganu ILihat sebelah
SLILIT

ST]LIT 22 3472/l

Fot
FJaniner's
Use
24 A team of 6 playersare to be selectedrandomlyfrom 7 girls and 4 boys.
Find the numberof ways the team can be formed if
Satupasukan terdiri daripada 6 orang pemain akan dipilih secara rawak daripada
7 orang perempuandan 4 orang lelaki. Cari bilangancara pasukanitu tlibentukjika

(a) there is no restriction,
tiada syarot dikenakan,

(b) the numberof girls is morethanthe number boys in the team.
of
pemainperemputn lebih ramai daripadapemain lelaki dalampasukanitu.

14marksl
14narkahl

24
r-:
I l4t
AnswerI Jawapan: (a) . . . . . . . . . . . . . . .

3472/1 O 2009 TRIAI- SPM Hak Cilta JabalanPelajaranNegeri Terengganu
[|,ihat sebelah
STILIT
95

SUIIT 23 3472t'l

tq Diagram showsa standard
25 graph'
normaldistribution LamLner's
L'se
graftaburan normalpiu*'ai.
Raiah 25 menuniukkan

Diagram 25
Rajah 25

The probabilityrepresented the areaofthe shaded
by regionis 0 7648'

Kebarangkalian yang tliwakili oleh luas kawasanberlorekiulah 0'7648'

Find / Cari
(a) P(z > i),
(b) the valueof ft.
nilai bagi k.
[3 marks]
13markahl

25
Answet/,lau,upan: (a) P(z
t--: r l
I t
(b) k=

H N DO F Q T ] E S ] O N P A P E R
I
IiERT'AS SOAI.AN TAMAT

lLihat sebelah
i472/l c:; -100t) Ncgeri Tl-rcnSganu
1l{lAl. SPM ll k tli|tiL.lirbaurr Pcl:tiaftrn
sul.lt'

SLII,IT 21 3472t1

INFORMATTONFOR CANDIDATES
MAKLUMAT UNTAK CALON

l. paper
This question of25 questions.
consists
Kertas soalon ini mengandungi soalan.
25

2. Answerall questions.
.Iawab sernuusoalen.

providedin the questionpaper'
Write your answersin the spaces
Tulisjawapan anda dalan ruang yang disediaktn dalam kprtas soalan'

Showyour working.It may help you to getmarks.
TunjukkanlangkahJangkahpenling dalam kefa mengiraanda. Ia boleh membanlu
markah.
anda untuk mendaPslkan

). lfyou wish to change your answerrcrossout the answerwork that you havedone'
Then wrile down the new answer.
Sekiranyaanda hendakmenukar iawapan, batalkan jau'apan yang telah dibuat'
Kemudian tulis jawaPan Yang baru

The diagramsin the questionsprovidedarenot drawn to scaleunlessstated.
Rajah yung nengiringi soalan tidak dilukis nengikut skala kecuali dinyatakan'

7 . The marksallocatedfor eachquestionare shown in brackets.
Markah yang diperuntukkanbagi setiapsoalanditunjukkandalam kurungan'

8 . A list of formulaeis providedon pages to 4.
2
Satusenarai rumusdi,sediakan halaman2 hing.ga
di 4.

tablesis provided.
9. A bookletoffour-figure mathematical
Buku sifir matematik empat angka disediakan.

calculator'
scientific
10. Youmayusea non-programmable
kalkulator
menggunakan
Andadihenarkan saintifikyanglidakbolehdiprogram'

ll. Hand thisquestion
in paperto invigilator theendof theexamination'
the at
kertassoalunini kepoda
Serahkan peperiksaan aLhirpeperiksaan'
pengowas di

NegeriTerengganu
Pelajaran
347211A 2009 TRIAL SPM Hak Cipta Jabatan SLILIT
97

74
SULIT 3472t1(.PP)

TERENGGANU
JABATANPELAJARAN

PEPERIKSAANPERCUBAAN SPM 2OO9 34721I
Kertas 1
PeraturanPemarkahan
Sept2009

g
Perllturall peilrarkahanini ntengalrdLrlrgi halamittt bcrcstak

34721(PP) .rr2009 SPtvl Cipto
TRIAL Hak Negeri
Pelajamn
Jabatan Tefengganir [Lihat sebelah
SULIT


3412t1(l>P)
stn-lT'

INSTRUCT IONS FOR F]XAMIN F]RS

I, MARKING GUIDII

1.I Mark all the anslvers.
1.2 Do not mark lvorking/ answerthal hasbecncancelled
workingis considercd final
the
l.i Answerwritten in the answerspace at the endofthe
or
allswer.
the working'
1.4 lull mark is given fi,'rthe correctanserwithout referringto
mark as statedin the
1.5 If the linal answer ls wrong, award the corrcspondingmaximunl
tnarking scheme.
l.6lfmoretlrenonefinalanswerisgiven'clroosethcanswerwiththehighestmarkUnless
statedotherwise in the marking schenre'
full mark is not
wrongly in the answerspace'
1.7 lf tlre final answerrs coffect,but stated
au'arded.

2. NOTATION
2 . 1 l u l l m a r k t b r e a c l r u e s t i o nn t h i sp a p e r s e i t h e 2 , i u 4
q i i r

2.2 If full mark is not awarded, following systetn used:
the is

83 - ct'
3 marksis awilrdedif the answerat this stagcis corre
B2 - 2 tnalks is awardedil'the answerat this stageis concct'
tst - 1 mark is awtrrded the answera1this stageis correcL
if
qucstion'
2 . 3 O n l y o n eo u l o f 8 3 , 8 2 o l B l i s a w a r t . l e bl r e a c h u e s t i o n r p a d o f a
lt q o

3.Acceptanswerscofrectto4significantfiguresunlessstatetlotherr,viseint|remarkingschenre.

4. rvhichare not given irr the markingscheme'
Acceptothercorrectmethods

5. in Melayrt
Acceptansrvers Bahasa

6. Calculatingtotal nlatKs

S e r ) r co r I ' u p u r I f
f I s c " r e l { ' r I ' i r l ) cIr ,^ ^ , , ,
I l{0

Pelaiaran retengsanu
Jabatan
cipta Negeri llihat seb,clah
sPMHak
rRIAL
317211{PP) io20os
SI]LIT


3 347?/1(Pt)
STILIT'

Mark Scheme E Marks

(a) 3

(b) (l

(a) 7 (r)

(b) 2 {2)
| -3x:7 or B1

', . - 8 or p<Itl75 (2)

( l 1 2 - 4 ( l ) ( 21 , ) 0 tll ((iive B0 lbr othcr than < 0)

k:6. 6 (3)

d+ 2a=-k, a(2a):8 (both) ald o: !2
(acccpta: 2)

,t'2u k tlr t,t(2n) 3 BI

OR

k:6,6 (3)

-k= 3a, 2l:8 (botlr) a n d c = t 2 B2
(accept 2)
ll-

(r - aX.{ 2/l :0 xnd " t 2m, ar+2i-0

I < 3 , 1 >6 (J) ({iive li2 tbr othett}ran1)


(PP
3.1?2/r )
ST]I,IT'

I (a) 9

(b) |
(l)

(1)
Mark Scheme

(c) r= I (l)

4, 42 (borh) t3)
I
I t r r 5 ) . ( t x l ) | l , { l ) I I ( l r ' k t 5 't ] t l } l l - l { )
.
1

;
I
J 1715r ( Ix
1 r) , ( l ) - t l ( l ) - { ( 5 rI 7 ( l r l J ' l9
'
sign)
tfor 82 thcre is rroatrsolute

l
, J I r 7 ( 5 r ( r X l , , l ( t ) I I ( t ) * l ( 5 ) 7 r I ) lI
)
)

i- or -0.11
- 125 (3)
16
I
- i a (Z r ) ' ) o r c q u i ra l . r t t
- B2
I
-
3: 13+i2-')1 :r rvith base3
Bl for any two out of thme irrdiccs

s l0
(a) 0.625 or ( 2 1 { d on ( , 1 ( c r p t . . )
a
ll lo

l 0 = r 6 ' or cqLriva
lent
antl PQ - 10 crn (value l0 seenanywherein
rvorking sPace) Bl

( b ) 45 cnt' (2) iigrroreLrnit)

l -
Aroa =. : ( l?l' +f/ + krllorv firr0' lll

t l
I L

(PP)
3,t7211 O 2OO9TRIAL EXAM SPI"'I BakciptaJabatan NegefiTerengga'ru [Lihat sebclah
Pelsiaran
sut.l'l'


j SI,ILIT

Marl< Scheme
3472!t(1'P)

I Marks

k:4 (21

3k-2 12 {tr 1+k,(3k 2')

4
- o r
(al i .33:l 0)
l -

thI 5/ (3) accept
53.997 na1
bU! 5i.99

JO 36
, r
! -
i - .0 . 3 3 1 3
3

a : 3 6 unal , : ,l
3
accept0.3333

Zp-rq- 2 (3)

2 l o g s / z + l o g r , t l o g 39 Ilz

lll fol either using log.,nn or log,, A
n

l
I
I I
347211(Pl'') @r
2009TRIAL
EXAMsPlvl HakciptaJabatan
Fetaja€n
Negeri
rerengganu lLiSat sebelal
SUI,I'


3412tr..|PP)
sUt.l '

Mark Schcme
)
/'t r
t
t -. - j
J
or (0'75,025) (3)
4 4)
3
1t) r - l X 2)-2 9r':t or equlval9lli

4)
ul lignore
2x - 1)(7) or equivalent
;

(al -7 (l)

(b) -6 (3)

1 llr(4) P(l)l-25 82 (subslitutc)

I ]5 Rl lor integration
[r.tl,'

(3)
ta, . - 1

', : lll
2
--)yt )0 82

'PX zxl c' BI (ignore+r' for 81)
'v--. - 2

? -
(b) 'r,: ?-a-r' - 2x-rl0 gg equivalenl (l)
,

(a) 2a+b

( 1 ) for corrcctlY sPotted
R
and labelled

P
I ,l

a
A

Terengganil
Negeri
sP[4 Hak CiptaJabaianPelajaran
rRIALEXAM lLihat scbclah
(PP)
341211 o 2oos sul,r'l'


' 3172/1(vPJ
stJI t'f

Mark Schcme X Marks

(a) i+3i (l)

(b) (i) .,/a0or 6 i25 or 2 Jt 0 (2)

-)
P^9- 2(i | 3j) q! cquivalent Il1

2 I
(ii) :il + Jt) or (2i + 6j)
#(ii3i) V'+{l J+o

2-i , j:i sr 0'3162+ 3i)
(i
J40 J40

0 . 1 5 8(1 ir 6 j ) o r 0 i l 6 2 i + 0 9 4 8 6 i
2 (1)

p : 3. q -- 25 (both) (3)

- rt, t)
('ornprr(': f I !I l 82
t l

n-2 o r c - l o g , ,1, 0 0 09 1 c : 3 B1

F r o m : l o g , uJ ' : l o g r o 0 0 0+ 2 l o g r ) x
1

;r = 0',90", 180" (4)

_t= 0.. I80" or _r.'90.

s i nr : 0 9g cos - i
r 82

? s i r . t ( c L r s .lr) - 0

-r
2 sin.tcc,s 2 sirl.r = {l lll
I
I
l

I
1
i

(PP,
347211 (.i 2009TR'AL EXAM SPM Hak CiplaJabatanPelaiaran Tereigganir
Negerl ll,ihat scbelah
SLLII


SUI,IT 3472/t(PPl

Mark Schcme X Marks
l
(a) Ql
1

(t I r)
-,
n rf ' ' . ' l - ,f l . r . 5 l B r
"
l2'a'n.J 5 rj/ lr 5 8/

o); e)
(t r r) ( t 4 3 )
- r J x-x
o I R1
l,t';"*J 2 5 8)

(a) 5040

ib) 3600
"P., t. x.2l)
7: {.61 IJI

(a) '1.62 (I)

(b) i 0 1 (3)
-(.,,' '(',, 'c'. r (' ' t{-'o t{',
I r x Bz

''f-'o 'tc,
tc'u
t or
'('r, (|,r 't:,*t{..'., Bl

ta) 0 . 1 0 i 8 (r)
(b) 1 . 2 6 (2)

0 li 14 or 0 8962 or 0 i0-18 or 0 ?352 BI

ENt) ()F Nl.{Rh. S(' tlllMlL

-f€rengganu
34?2/1 (PP! g2009TRjALFXAM
sP[,] flakcipta..]abaian Negeri
Pelajaran
sul.i I


Panduan Lengkap
e-Book KERTAS SOALAN RAMALAN MATEMATIK SPM 2010


e-Book KERTAS SOALAN RAMALAN MATEMATIK SPM mengandungi

• 2 set soalan ramalan beserta skema jawapan

• 8 set soalan soalan percubaan negeri 2009 beserta skema jawapan

• Soalan ramalan 13 matapelajaran SPM 2009 beserta skema jawapan

• 5 set soalan tahun-tahun lepas 2005-2009 beserta skema jawapan

Cuma RM20.00 sahaja

Untuk keterangan lanjut dan tempahan sila layari


Panduan Lengkap
e-Book KERTAS SOALAN RAMALAN MATEMATIK TAMBAHAN 2010

e-Book KERTAS SOALAN RAMALAN MATEMATIK TAMBAHAN SPM
mengandungi:

1. 2 set soalan ramalan beserta skema jawapan

2. 8 set soalan soalan percubaan negeri 2009 beserta skema jawapan

3. Soalan ramalan 13 matapelajaran SPM 2009 beserta skema jawapan

4. 5 set soalan tahun-tahun lepas 2005-2009 beserta skema jawapan

Cuma RM20.00 sahaja

Untuk keterangan lanjut serta tempahan sila layari


Koleksi soalan addmath kertas1

More Related Content

What's hot

Viewers also liked

Similar to Koleksi soalan addmath kertas1

Recently uploaded

Koleksi soalan addmath kertas1