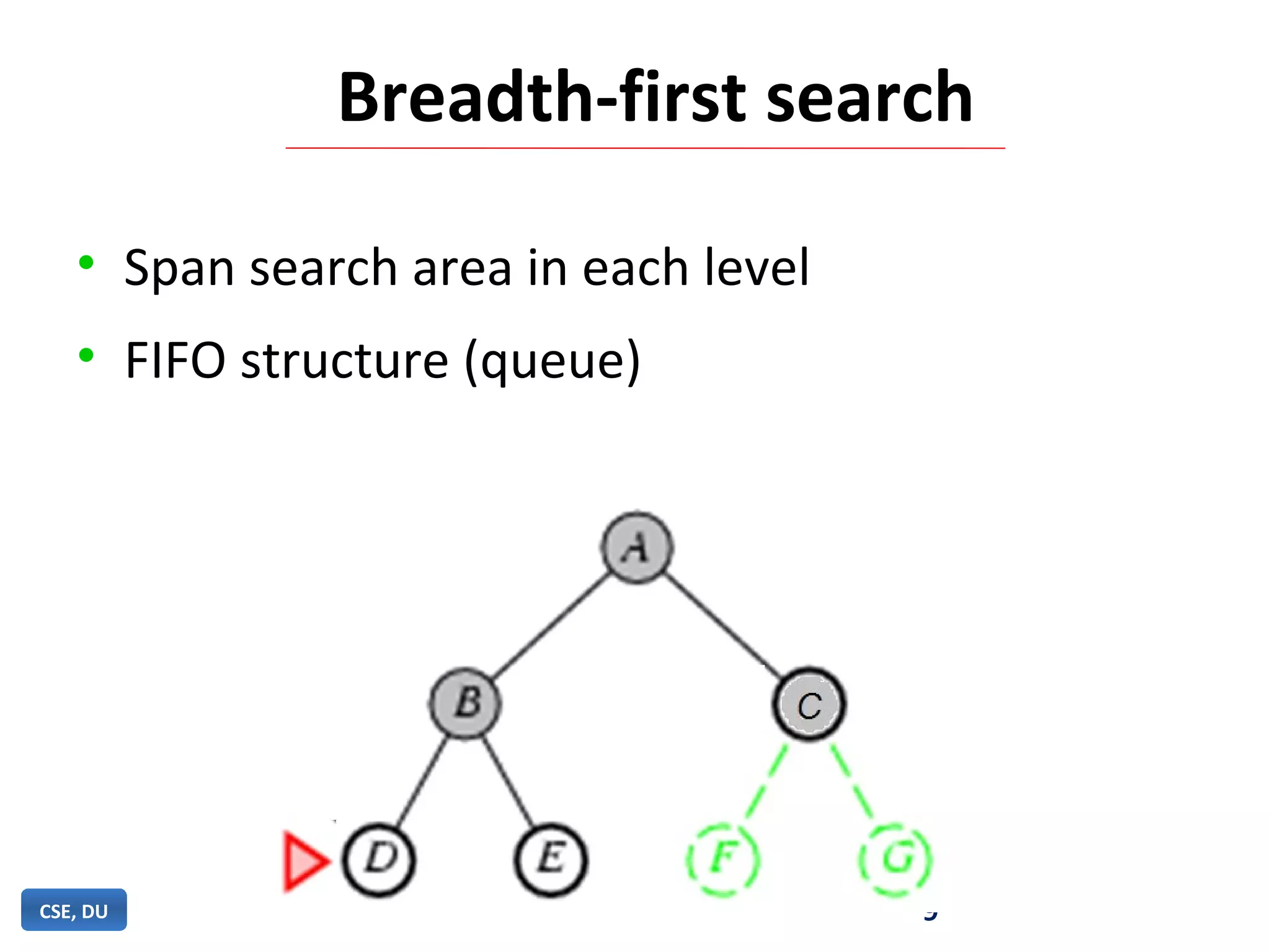
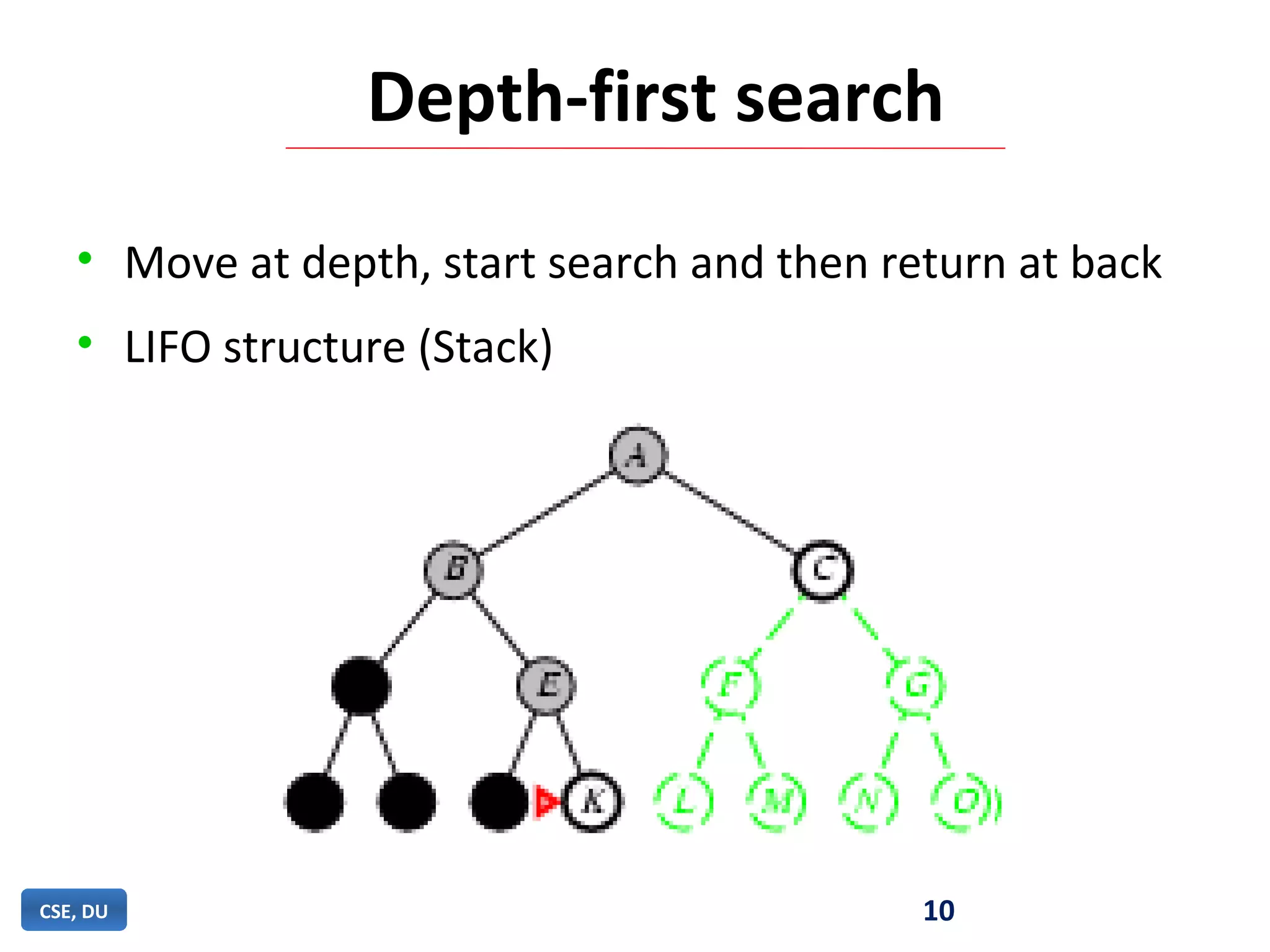
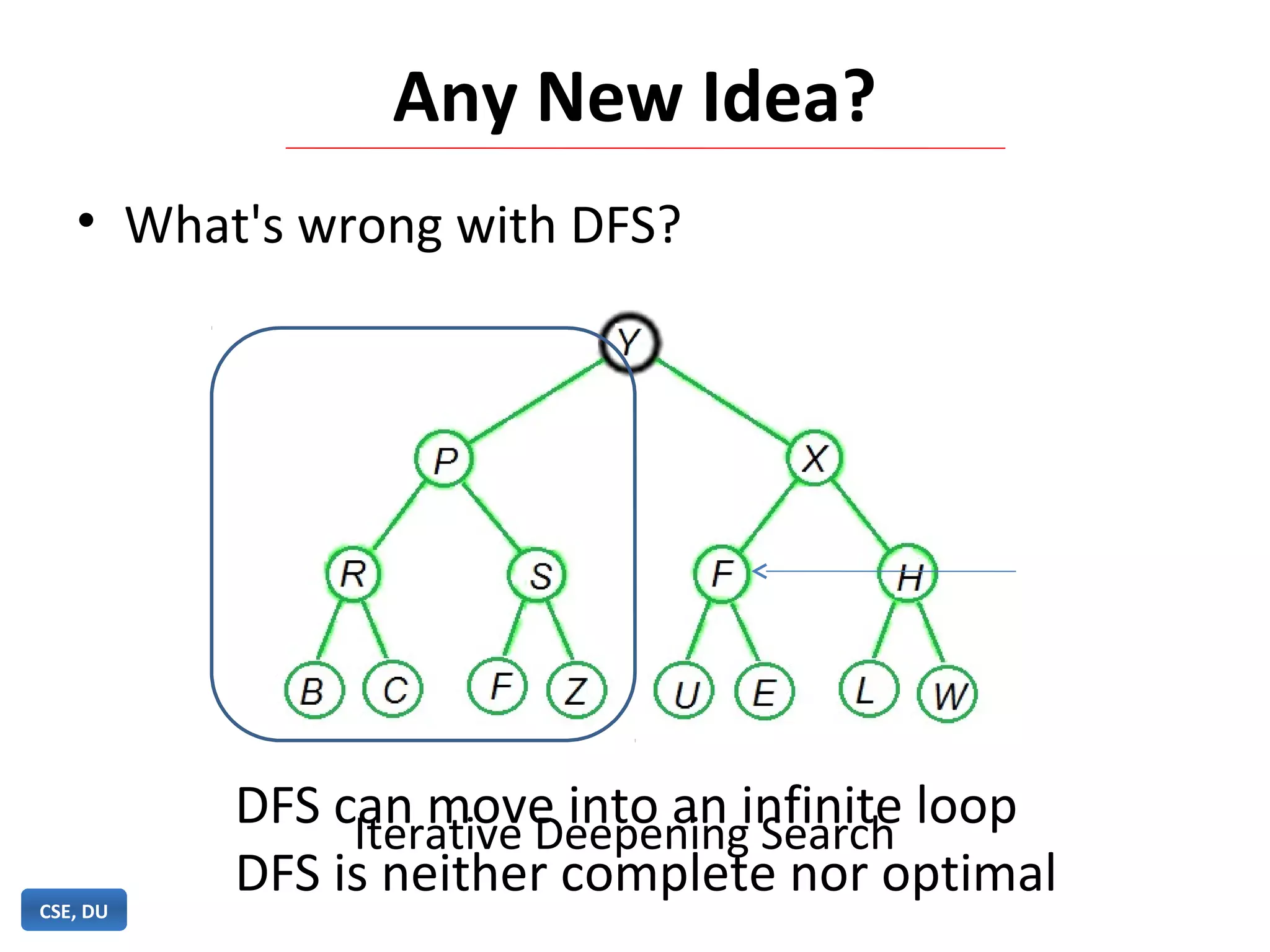
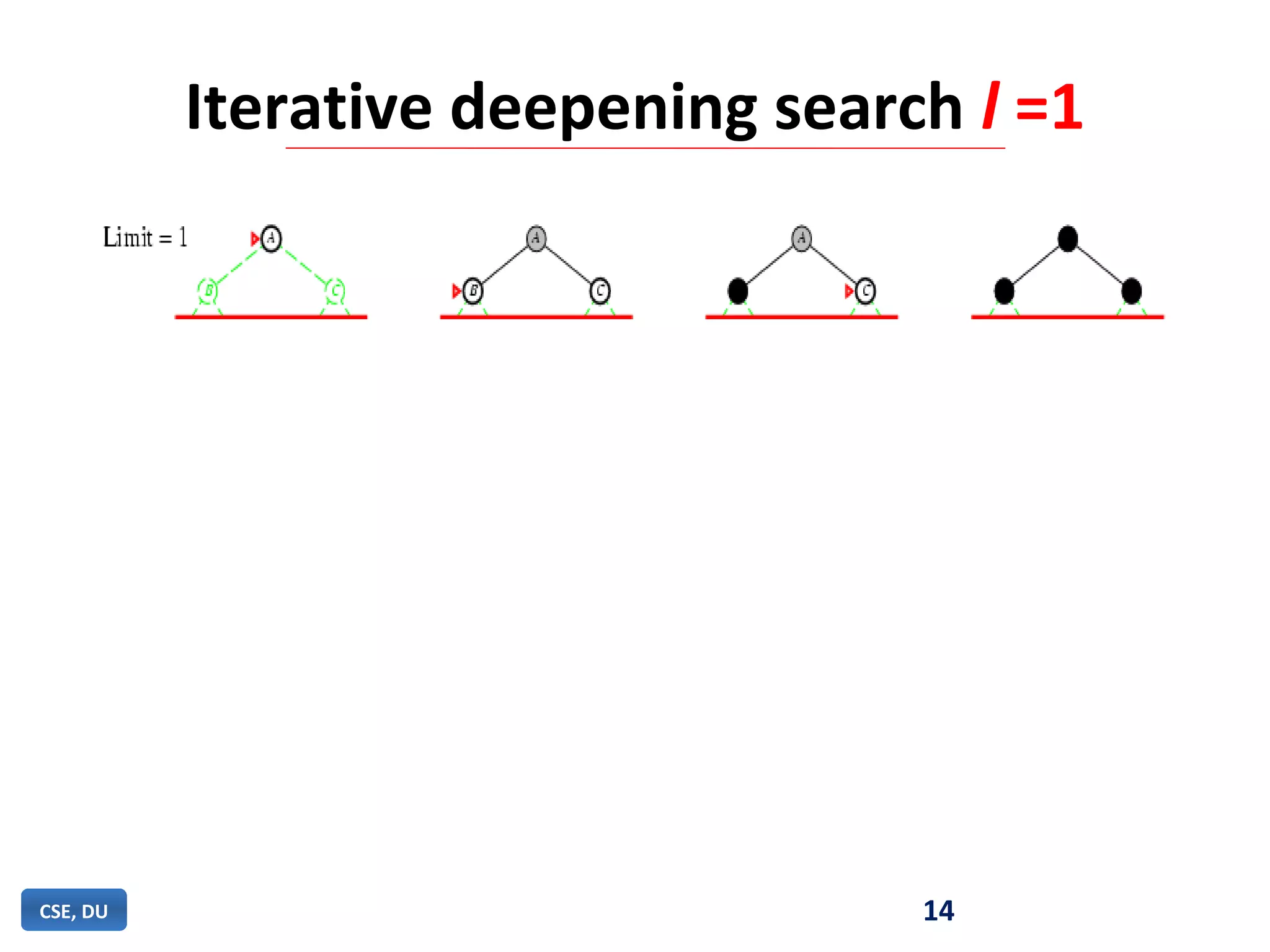
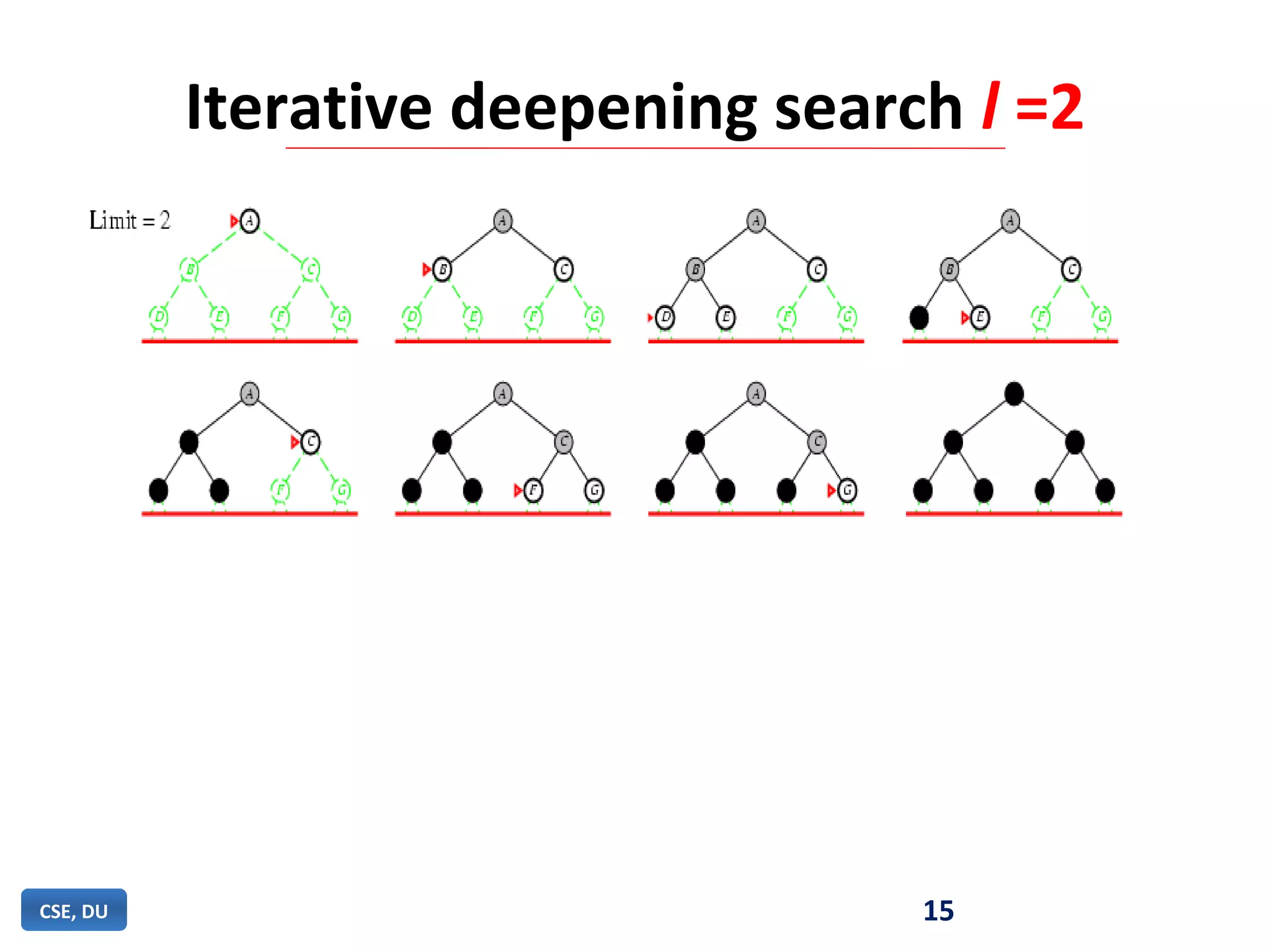
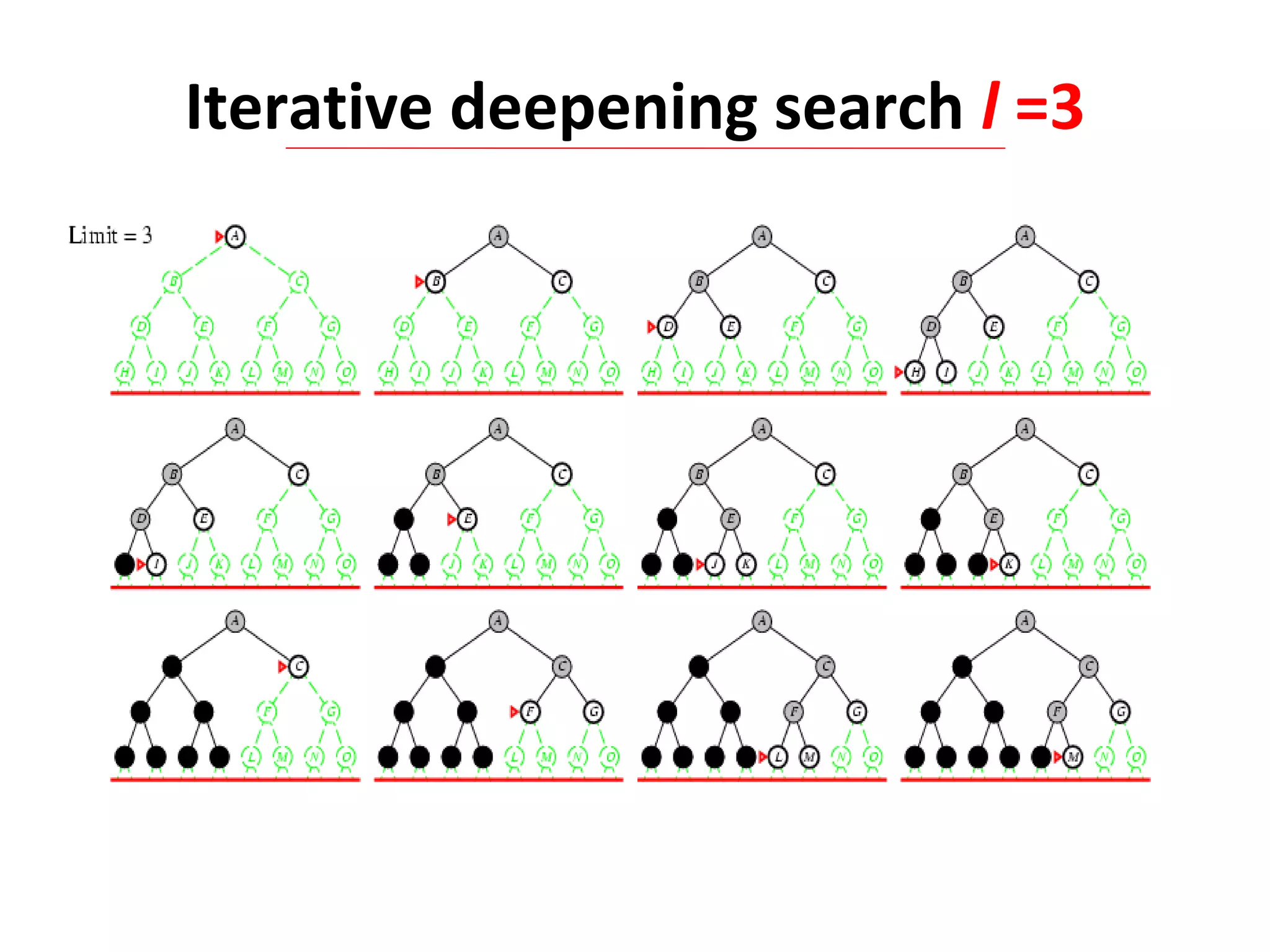
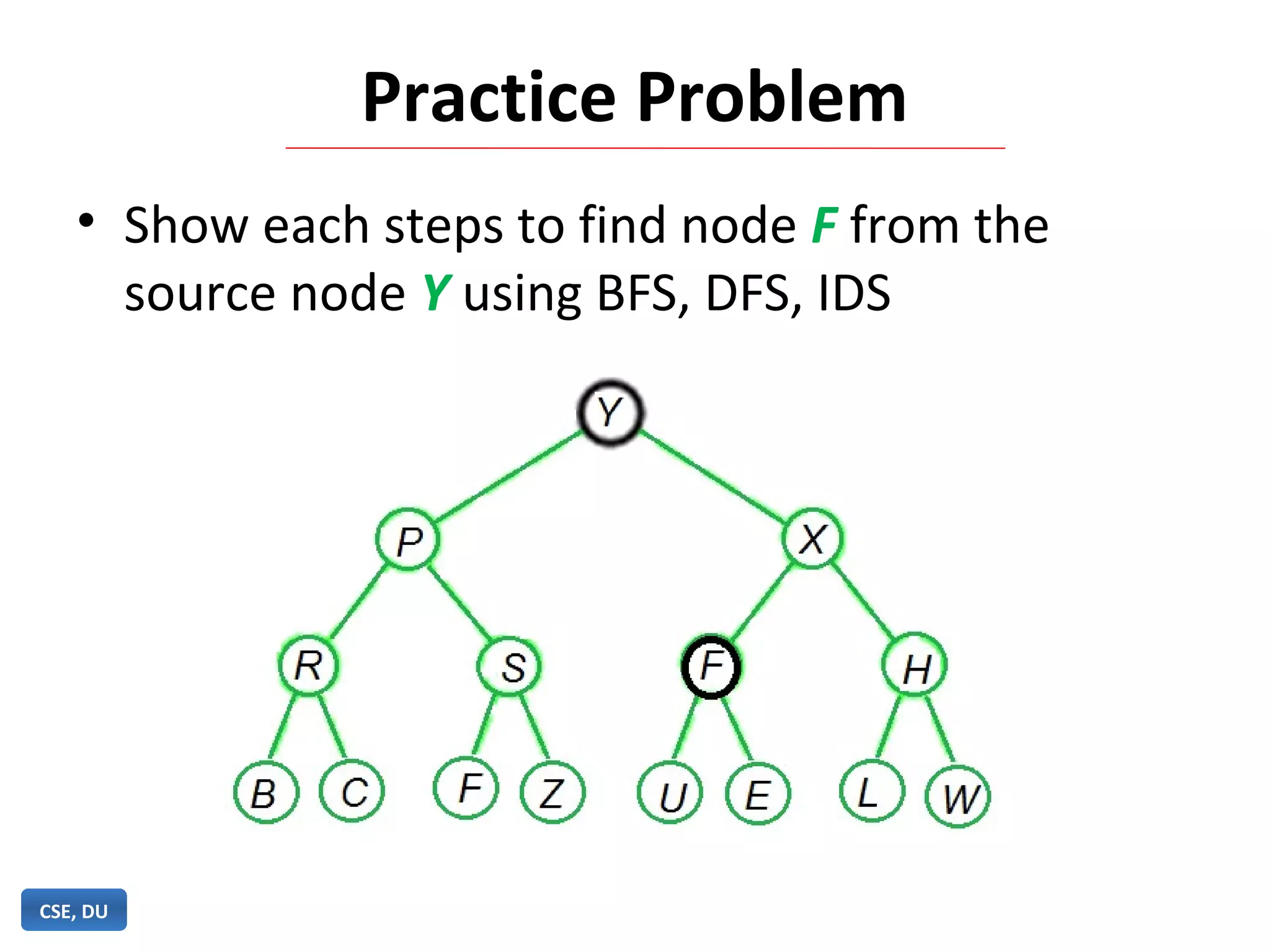
Iterative deepening search (IDS) is an algorithm that combines the completeness of breadth-first search with the memory efficiency of depth-first search. IDS performs an exhaustive depth-first search, increasing the depth limit by one each iteration, until the goal is found. IDS is guaranteed to find a solution if one exists, uses less memory than breadth-first search by limiting the depth of search at each iteration, and is more efficient than depth-first search which can get stuck in infinite loops.

1. Iterative Deepening Search
Ashis Kumar Chanda
Department of Computer Science and Engineering
University of Dhaka

2. Topics
• Introduction
• Searching Methods
• Iterative Deepening Search
• Properties
• Analysis
• Summary
CSE, DU

3. Introduction
• Search an item in Graph
CSE, DU
Air flight system
• Each city represents a vertex
• Each direct flight represents an edge

4. Graph
• A well recognized tool in modeling problems
• Consist of:
– Vertices can be considered locations.
– Edges represent connections connections.
CSE, DU
D
E
A
C
F
B
Vertex
Edge

5. Graph Representation
• How will we represent a graph in computer?
1. Adjacency Matrix
2. Use a 2D matrix to represent the
graph
3. Adjacency List
4. Use a 1D array of linked lists
5CSE, DU

6. Adjacency Matrix
A[i][j] = 1 if there is an edge connecting vertices i,j
A[i][j] = 0 otherwise
6CSE, DU

7. Adjacency List
The adjacency list is an array A[0..n-1] of lists,
where n is the number of vertices in the graph
7CSE, DU

8. Searching Methods
• Most common methods
– Breadth First Search (BFS)
– Depth First Search (DFS)
CSE, DU

9. Breadth-first search
• Span search area in each level
• FIFO structure (queue)
9CSE, DU

10. Depth-first search
• Move at depth, start search and then return at back
• LIFO structure (Stack)
10CSE, DU

11. Any New Idea?
• What's wrong with DFS?
CSE, DU
Iterative Deepening Search
DFS can move into an infinite loop
DFS is neither complete nor optimal

12. Iterative Deepening Search
• IDS is similar to DFS
• Depth is not known
• increasing the depth limit with each iteration
until it reaches d, the depth of the goal state
CSE, DU

13. Iterative deepening search l =0
13CSE, DU

14. Iterative deepening search l =1
14CSE, DU

15. Iterative deepening search l =2
15CSE, DU

16. Iterative deepening search l =3

17. Pseudo-code
CSE, DU
Input: Graph root, goal
Output: solution or failure
IDS(root, goal)
{
for(i=0 to infinite)
{
DLS(root, goal, depth=i)
}
}
depth-limited DFS (called DLS);

18. Properties
where b is the branching factor and d is the depth of goal
CSE, DU
Criteria Properties of IDF
Complete search Yes
Required Time O(bd )
Memory Space O(bd)
Optimal Solution Yes

19. Analysis
• Applicable when there is a large search space
and depth is not known
• The main advantage of IDS in game tree
searching
• IDS combines depth first search’s space
efficiency and breadth first search’s complete
-ness
CSE, DU

20. Practice Problem
• Show each steps to find node F from the
source node Y using BFS, DFS, IDS
CSE, DU

21. Summary
• Representation of Graph model
• Searching model BFS, DFS
• Iterative Deepening Search Model is
combination of BFS, DFS
• Better than DFS and needs less space than BFS
CSE, DU

22. About Me
• Research Topics:
- Flexible Periodic Pattern Mining
- Closed Frequent Pattern Mining
• ML course of Stanford University
• Won several Software Contests
• Solve Hundreds ACM problem
CSE, DU
Story writing Code Rage Badge
www.chandacse.blogspot.com

23. References
CSE, DU
- Artificial Intelligence a Modern Approach
by Russell and Norvig
- Introduction to Algorithm by Cormen
- Fundamentals of Computer Algorithms by
Ellis; Sahni, Sartaj Horowitz
- http://en.wikipedia.org/wiki/Iterative_deepening_depth-
- http://artint.info/html/ArtInt_62.html
- http://will.thimbleby.net/algorithms/doku.php?id=iterati