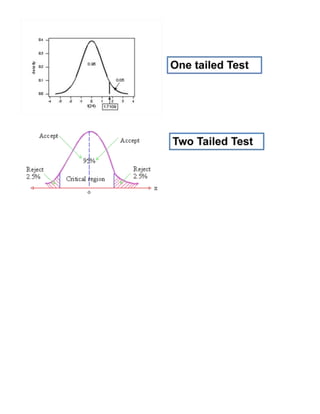
Inferential statistics allow researchers to draw conclusions about populations based on data from samples. They estimate population parameters and test hypotheses about populations that extend beyond the sample data. Hypothesis testing provides objective criteria for deciding whether to accept or reject research hypotheses as true or false based on the probability that any observed differences are due to chance. It involves selecting a test statistic, significance level, computing the test statistic, and comparing it to critical values to determine whether to reject the null hypothesis. Type I and Type II errors can occur but the significance level controls the risk of Type I errors.

1. INFERENTIAL STATISTICS
Inferential Statistics
provide a means for drawing conclusions about a population given data from a sample
trying to reach conclusions that extend beyond the immediate data alone
to make judgments of the probability that an observed difference between groups is a dependable one or that
might have happened by chance
Probabilistic estimates involve some error, but inferential statistics provide a framework for making objective
judgments about their reliability.
Researchers use inferential statistics to estimate population parameters from sample statistics.
Sampling Distributions
To estimate population parameters, it is clearly advisable to use representative samples, and probability
samples are the best way to get representative samples.
Inferential statistics are based on the assumption of random sampling from populations, an assumption that is
widely violated.
Even when random sampling is used, sample characteristics are seldom identical to population characteristics.
Example
 Suppose we had a population of 50,000 nursing school applicants whose mean score on a standardized entrance
exam was 500 with an SD of 100.
 Suppose we had to estimate these parameters from the scores of a random sample of 25 students.
 Would we expect a mean of exactly 500 and an SD of 100 for this sample?
 Let us the sample mean is 505. If a new random sample were drawn, we might obtain a mean value such as 497.
 The tendency for statistics to fluctuate from one sample to another reflects sampling error.
Sampling error refers to differences between population values (such as the average age of the population) and sample
values (such as the average age of the sample)
So what do we do now!!? If average value computed from a single sample can be erroneous!?
Let’s consider this:
 Consider drawing a sample of 25 students from the population of 50,000, calculating a mean, replacing the
students, and drawing a new sample.
 Each mean is considered a datum.
 If we drew 10,000 samples, we would have 10,000 means (data points) .
 This distribution could be used to construct a frequency polygon and it is called sampling distribution of the
mean.
Statistical Inference two techniques:
1. Estimation of Parameters
2. Hypothesis Testing
Hypothesis Testing
Allows objective decisions if results likely reflect chance sample differences or true differences in a population.
provides objective criteria for deciding whether research hypotheses should be accepted as true or rejected as
false
Hypothesis testing is based on rules of negative inference.
Null hypothesis (Ho) = No
Alternative hypothesis (H1) = There is

2. If null hypothesis is rejected, alternative hypothesis is accepted
If null hypothesis is accepted, alternative hypothesis is rejected
Steps in Hypothesis Testing
1. selecting an appropriate test statistic
2. selecting the level of significance
3. computing a test statistic
4. determining the degree of freedom
5. comparing the test statistic to a tabled value
Errors in Hypothesis Testing
Type I Error
- rejecting a “true” null hypothesis
- is a false positive conclusion
Type II Error
- accepting of a “false” null hypothesis
- is a false negative conclusion
Level of Significance
Also known as Significance Level
Researchers control the risk of Type I error by selecting a level of significance
Pre – decided prior to testing hypothesis to avoid bias
Referred to as Alpha
Commonly used level .05 and .01
0.05 sig. level = 100 samples drawn from population, “true” null hypothesis would be rejected 5 times
5% chance of Type 1 error (rejecting a true null)
0.01 sig level = 1 sample out of 100 would the null wrongfully rejected
1 % chance of Type 1 error (rejecting a true null)
0.01 or 0.001 for important decisions
Lowering risk for Type I error increases risk for Type II error (accepting false null hypothesis)
also known as the Acceptable Error
is compared against the Probability of Error (P Value)
P Value - is the estimated probability of rejecting the null hypothesis (H0) of a study question when that hypothesis is
true.
The term significance level (alpha) is used to refer to a pre-chosen probability and the term "P value" is used to indicate
a probability that you calculate after a given study.
Critical Region
Reject null if test statistics falls at or beyond the limits of the critical region
Not really manually computed
Every statistic there is theoretical distribution to which the computed test stat value is compared
STATISTICALLY SIGNIFICANT = test stat beyond critical limit