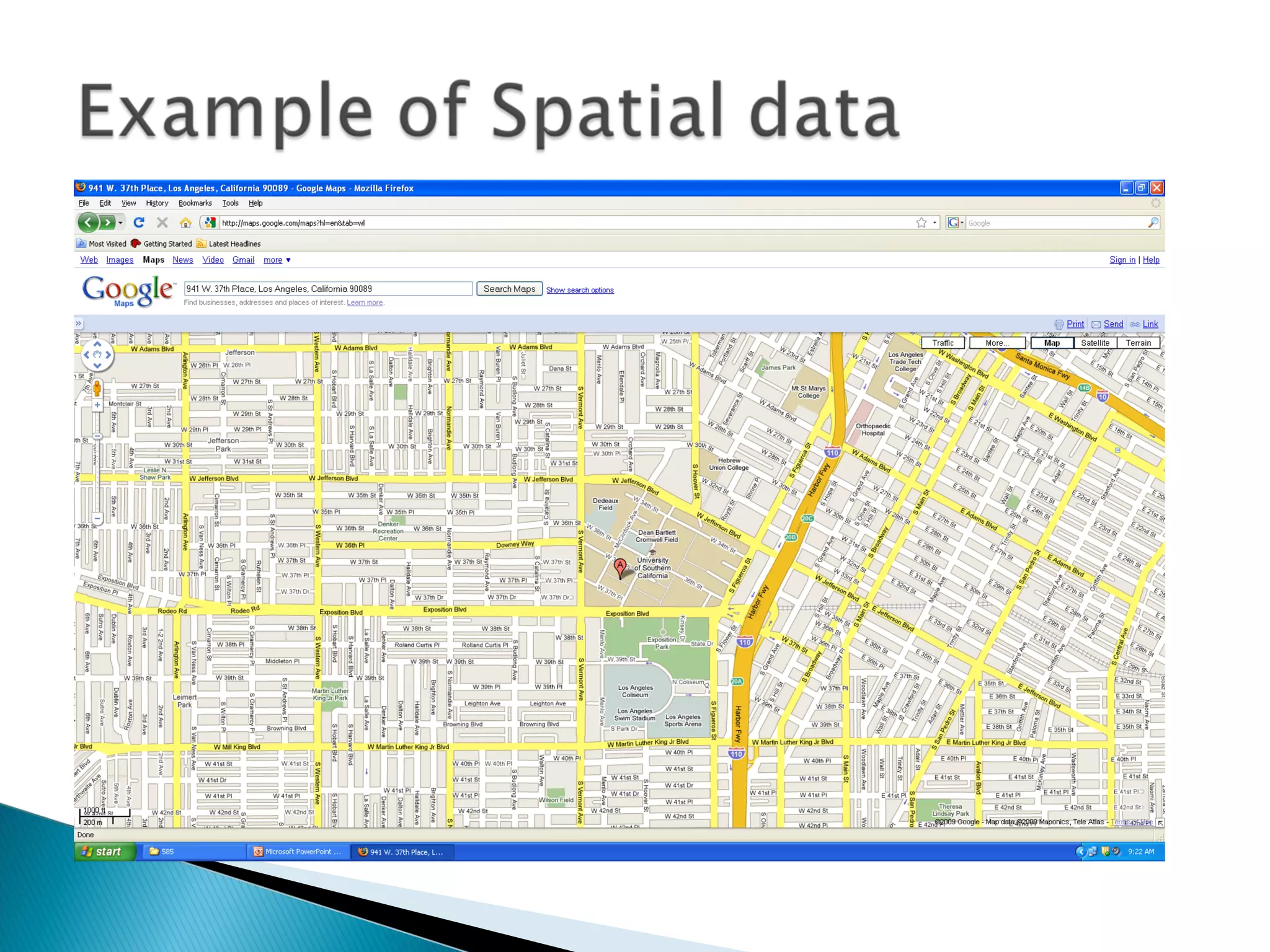
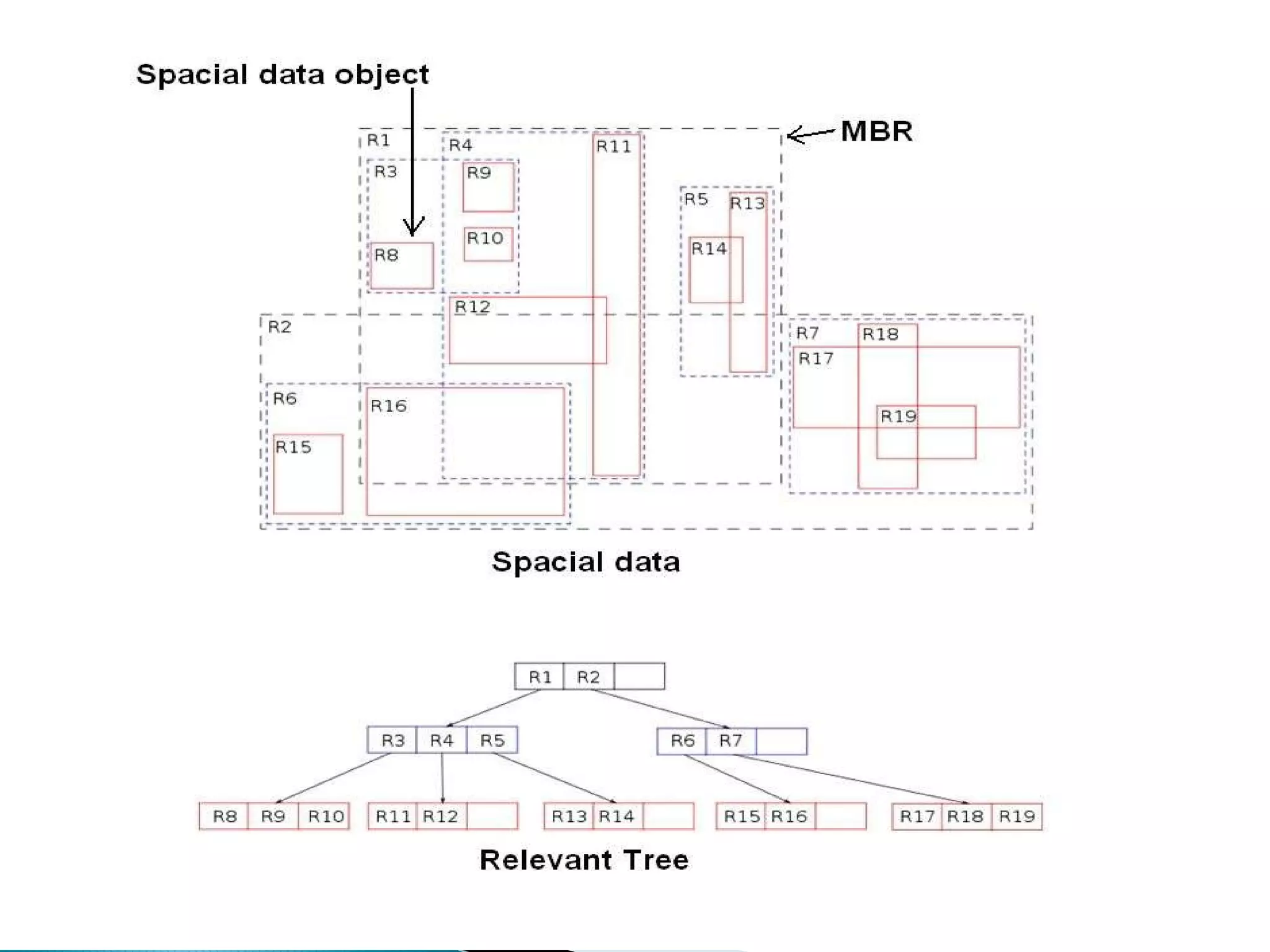
The document discusses R-trees, a data structure used to index multi-dimensional spatial data. R-trees allow for efficient searching of spatial data by grouping data into minimum bounding rectangles (MBRs) and storing them in a tree structure based on these envelopes. The tree structure resembles a B+-tree, with internal nodes containing pointers to child nodes or data records. R-trees provide efficient search, insertion, and deletion of spatial data objects through operations on the tree structure and splitting or merging of nodes as needed.

1. Vivek Kantariya (09bce020) Guided by : Prof. Vibha Patel

2. Manage large data Provide faster access Easy search Reduce unwanted memory access Proper memory allocation Increase efficiency

3. It contains a search key and a pointer. Search key - an attribute or set of attributes that is used to look up the records in a file. Pointer - contains the address of where the data is stored in memory.

4. Five Factors involved when choosing the indexing technique: access type access time insertion time deletion time space overhead

5. Access type - is the type of access being used. Access time - time required to locate the data. Insertion time - time required to insert the new data. Deletion time - time required to delete the data. Space overhead - the additional space occupied by the added data structure.

6. It is for multi- dimension data. Used to describe 2D or 3D objects. Real world usage. Examples are : R tree , R+ tree , KD tree , A tree , Hilbert tree , etc

7. Computer Aided Design (CAD) Geographic applications (like maps) Multimedia Applications (like X-rays) Biological Databases

8. Any Type of Geometry Point City Line Trail Polygon Border A Collection of Geometries Ski Resort Trails Any Coordinate System Meters Pixels WGS84 (GPS)

10. Proposed by Antonin Guttman UC Berkley All Spatial Data Enveloped Minimum Bounding Rectangle (MBR) Stored and Indexed According to MBR Structure Resembles B+-tree Height Balanced

11. For an index record <I, tuple-identifier> I = (I 0 , I 1 , … I n ) n = Number of Dimensions in the Geometry Each I is a set of the form [a,b] describing the range of the rectangle along the dimension a or b can be equal to infinity Tuple-identifier points to a record Non-leaf nodes are in the form: <I, child-pointer>

12. M is the maximum number of entries in one node m specifies the minimum number of entries in a node , where m ≤ M/2 Properties : Every Leaf Node Contains Between m and M index records unless it is root. For each index record, <I, tuple-identifier> in a leaf node is the smallest rectangle that spatially contains the n-dimensional data object.

13. Every non-leaf node has between m and M children unless it is the root. For each entry <I, child-pointer> in a non-leaf node, I is the smallest rectangle that spatially contains the rectangles in the child nodes. The root node has at least two children unless it is a leaf. All leaves appear on the same level.

15. Search Insert Delete Nearest Neighbor

16. Given R-tree with root T and and all records overlap with Search rectangle S. If T is not leaf, check each entry E to determine whether Ei overlaps with S. For all overlapping entries invoke search on each of them with root as node pointed by Ep. If T is a leaf check each entry E. If it overlaps output it.

17. Start at the root node Select the child that needs the least enlargement in order to fit the new geometry. Repeat until at a leaf node. If leaf node has available space then insert.

18. Else split the entry into two nodes. Update parent nodes Update the entry that pointed to the node with a new MBR [ Minimum Bounding Rectangle ] . Add a new entry for the second new node If there is no space in the parent node, split and repeat.

19. Make sure nodes are split so they cover the smallest possible area. Split should minimize average search time. GOOD SPLIT! BAD !

20. Remove index node E from R-Tree. Find node containing record. Remove E. If node contains fewer than m records remove the node and add it to Queue. Move up and do the same reducing covering rectangles. Reinsert all records from Queue.

21. Split Entries in the tree so that there is no overlap No more multiple paths to reach a solution Child pointers duplicated within the tree R-Tree MBRs R+-Tree MBRs

22. Do not split nodes on insert Take entries from the overfull node and reinsert them into the tree Changes MBRs Saves time and possibly rebalances the tree

23. www.ieeexplore.ieee.org A NEW APPROACH TO CREATING SPATIAL INDEX WITH R-TREE by Ze-Bao Zhang, Jian-Pei Zhang, Jing Yang, Yue Yang A NEW VARIATION OF R-TREE FOR INDEXING SPACIAL DATA IN GIS by Chen Yongkang , Zhou Xintie , Shi Tailai , Feng Xiaoming http://wikipedia.org/wiki/R_tree