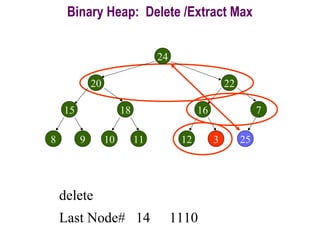
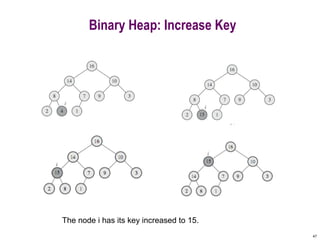
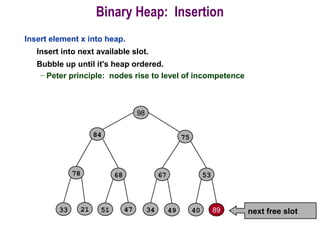
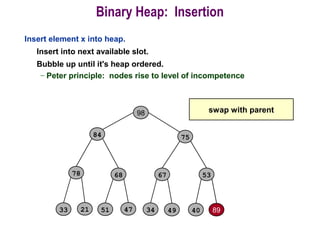
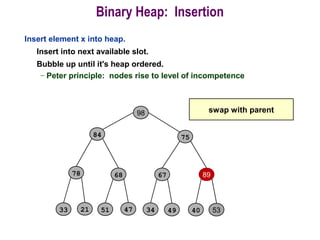
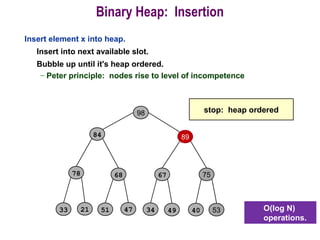
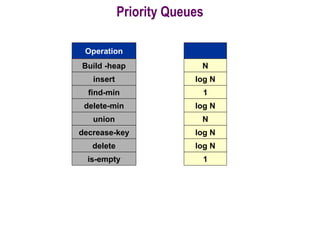
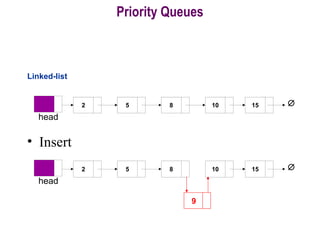
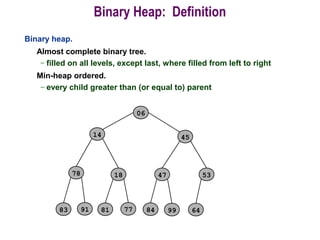
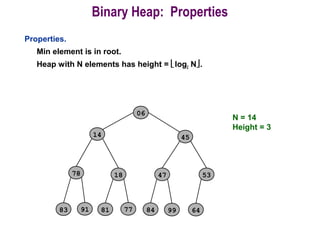
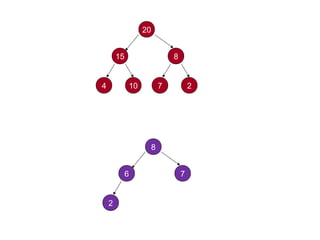
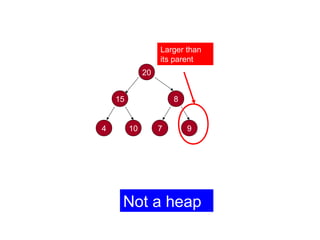
This document provides information about priority queues and binary heaps. It defines a binary heap as a nearly complete binary tree where the root node has the maximum/minimum value. It describes heap operations like insertion, deletion of max/min, and increasing/decreasing keys. The time complexity of these operations is O(log n). Heapsort, which uses a heap data structure, is also covered and has overall time complexity of O(n log n). Binary heaps are often used to implement priority queues and for algorithms like Dijkstra's and Prim's.

1. HEAPS

2. Priority Queues
Linked-list
2 5 8 10 15 ∅
head
• Insert
2 5 8 10 15 ∅
head
9

3. Priority Queues
Supports the following operations.
Insert element x.
Return min/max element.
Return and delete minimum/maximum element.
Increase/Decrease key of element x to k.
Max/Min-HEAPIFY
BUILD-Max/Min-HEAP
HEAPSORT
Applications.
Dijkstra's shortest path algorithm.
Prim's MST algorithm.
Event-driven simulation.
Huffman encoding.
Heapsort.
. . .

4. Time Complexity
Insert:
Delete:
n deletions and
insertions:
O(n)
O(n2
)
O(1)

5. Heap
A max (min) heap is a complete
binary tree such that the data stored
in each node is greater (smaller) than
the data stored in its children, if any.

6. Heap Types
Max-heaps (largest element at root), have the max-heap property:
for all nodes i, excluding the root:
A[PARENT(i)] ≥ A[i]
Min-heaps (smallest element at root), have the min-heap property:
for all nodes i, excluding the root:
A[PARENT(i)] ≤ A[i]

7. Binary Heap: Definition
Binary heap.
Almost complete binary tree.
– filled on all levels, except last, where filled from left to right
Min-heap ordered.
– every child greater than (or equal to) parent
06
14
78 18
81 7791
45
5347
6484 9983

8. Binary Heap: Properties
Properties.
Min element is in root.
Heap with N elements has height = log2 N.
06
14
78 18
81 7791
45
5347
6484 9983
N = 14
Height = 3

9. 20
815
4 10 7 2
8
76
2

10. 20
815
4 10 7 9
Larger than
its parent
Not a heap

11. 25
1210
59 711
1 6 3 8
Missing left
child
Not a complete tree – Not a heap

12. 1
32
54 76
8 9 10 11 12
Where to add the next
node?
How to find it?
Complete Binary Tree

13. 1
32
54 76
8 9 10 11 12 13 14 15
1 0001 6 0110 11 1011
2 0010 7 0111 12 1100
3 0011 8 1000 13 1101
4 0100 9 1001 14 1110
5 0101 10 1010 15 1111
After the first 1 from left: 0 – left; 1 –

14. 1
32
54 76
8 9 10 11 12
Next 13
1101
1
3
1
6
3
13
6
1
3
1
7
3
14
7
Next 14
1110

15. Binary Heaps: Array Implementation
Implementing binary heaps.
Use an array: no need for explicit parent or child pointers.
– Parent(i) = i/2
– Left(i) = 2i
– Right(i) = 2i + 1
06
14
78 18
81 7791
45
5347
6484 9983
1
2 3
4 5 6 7
8 9 10 11 12 13 14

16. 1
32
54 76
8 9 10 11 12
Storing a Complete Binary Tree in an Array
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
for any node at index i
parent = i/2 left child = i * 2 right child = i*2+1

17. Binary Heap: Insertion
Insert element x into heap.
Insert into next available slot.
Bubble up until it's heap ordered.
– Peter principle: nodes rise to level of incompetence
06
14
78 18
81 7791
45
5347
6484 9983 42 next free slot

18. Binary Heap: Insertion
Insert element x into heap.
Insert into next available slot.
Bubble up until it's heap ordered.
– Peter principle: nodes rise to level of incompetence
06
14
78 18
81 7791
45
5347
6484 9983 4242
swap with parent

19. Binary Heap: Insertion
Insert element x into heap.
Insert into next available slot.
Bubble up until it's heap ordered.
– Peter principle: nodes rise to level of incompetence
06
14
78 18
81 7791
45
4247
6484 9983 4253
swap with parent

20. Binary Heap: Insertion
Insert element x into heap.
Insert into next available slot.
Bubble up until it's heap ordered.
– Peter principle: nodes rise to level of incompetence
06
14
78 18
81 7791
42
4547
6484 9983 53
stop: heap ordered
O(log N)
operations.

21. Binary Heap: Decrease Key
Decrease key of element x to k.
Bubble up until it's heap ordered.
06
14
78 18
81 7791
42
4547
6484 9983 53 O(log N)
operations.

22. Binary Heap: Delete Min
Delete minimum element from heap.
Exchange root with rightmost leaf.
Bubble root down until it's heap ordered.
– power struggle principle: better subordinate is promoted
06
14
78 18
81 7791
42
4547
6484 9983 53

23. Binary Heap: Delete Min
Delete minimum element from heap.
Exchange root with rightmost leaf.
Bubble root down until it's heap ordered.
– power struggle principle: better subordinate is promoted
53
14
78 18
81 7791
42
4547
6484 9983 06

24. Binary Heap: Delete Min
Delete minimum element from heap.
Exchange root with rightmost leaf.
Bubble root down until it's heap ordered.
– power struggle principle: better subordinate is promoted
53
14
78 18
81 7791
42
4547
6484 9983
exchange with left child

25. Binary Heap: Delete Min
Delete minimum element from heap.
Exchange root with rightmost leaf.
Bubble root down until it's heap ordered.
– power struggle principle: better subordinate is promoted
14
53
78 18
81 7791
42
4547
6484 9983
exchange with right child

26. Binary Heap: Delete Min
Delete minimum element from heap.
Exchange root with rightmost leaf.
Bubble root down until it's heap ordered.
– power struggle principle: better subordinate is promoted
14
18
78 53
81 7791
42
4547
6484 9983
stop: heap ordered
O(log N)
operations.

27. delete
Last Node# 14 1110
25
2420
1815 716
8 9 10 11 12 16
22
3
7
3
25
3
24
22
3
3
16
25
Binary Heap: Delete /Extract Max

28. 28
Binary Heap: Delete /Extract Max

29. Max-Heapify Example
98
4186
13 65
9 10
32 29
44 23 21 17
index 1 2 3 4 5 6 7 8 8 10 11 12
value 98 86 41 13 65 32 29 9 10 44 23 2117
17
17
children of root: 2*1, 2*1+1 = 2, 3
17
86
86
left child is
greater
??
? ?
right child is
greater
17
65
children of 2: 2*2, 2*2+1 = 4, 5
17
44
1765 1744

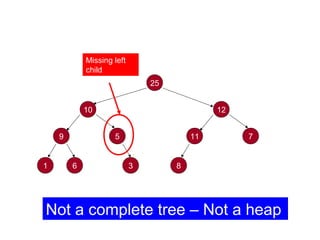
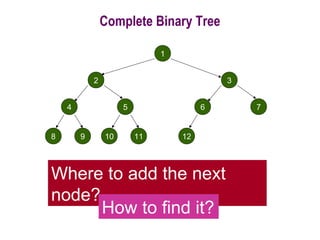
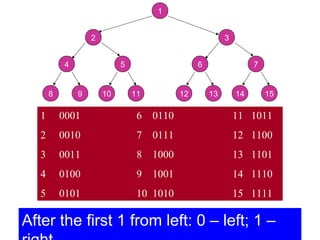
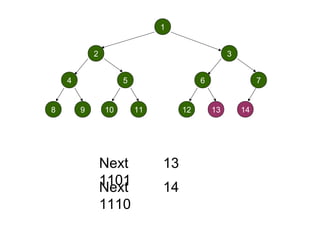
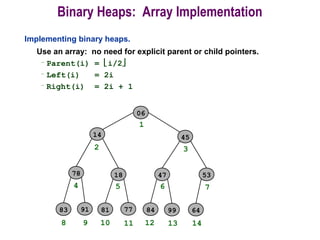
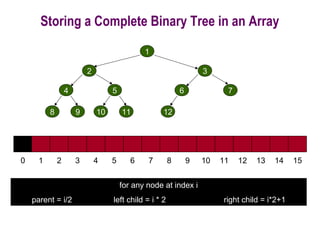
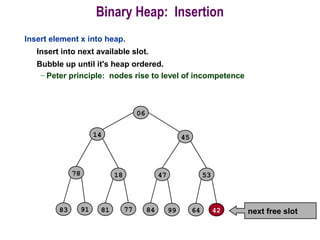
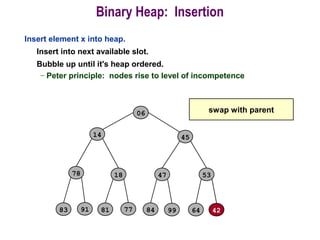
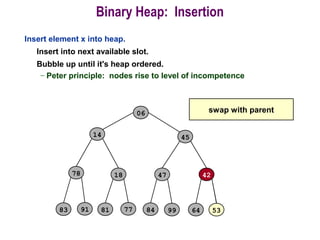
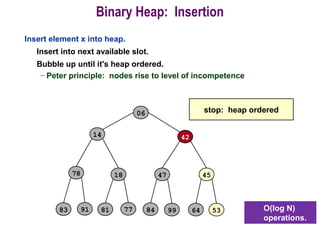
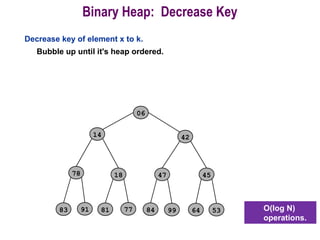
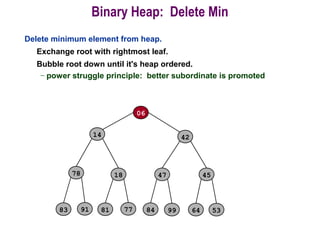
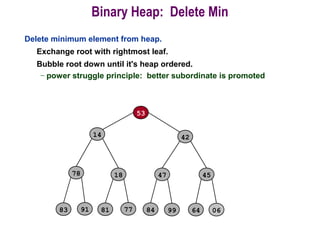
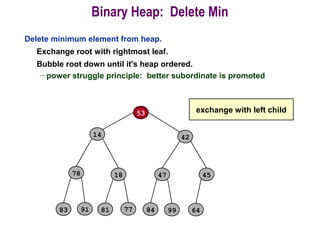
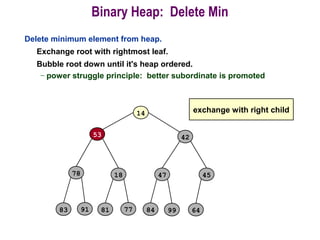
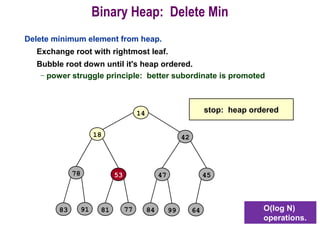
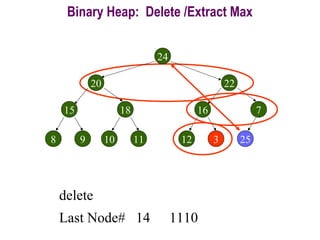
30. Procedure MaxHeapify
MaxHeapify(A, i)
1. l = left(i);
2. r = right(i);
3. if (l ≤ heap-size[A] && A[l] > A[i])
4. largest = l;
5. else largest = I;
6. if (r ≤ heap-size[A] && A[r] > A[largest])
7. largest = r;
8. if (largest != i)
9. Swap(A[i], A[largest])
10. MaxHeapify(A, largest)
MaxHeapify(A, i)
1. l = left(i);
2. r = right(i);
3. if (l ≤ heap-size[A] && A[l] > A[i])
4. largest = l;
5. else largest = I;
6. if (r ≤ heap-size[A] && A[r] > A[largest])
7. largest = r;
8. if (largest != i)
9. Swap(A[i], A[largest])
10. MaxHeapify(A, largest)
Assumption:
Left(i) and Right(i) are
max-heaps.

31. MaxHeapify – Example
26
14 20
24 17 19 13
12 18 11
14
14
2424
14
14
1818
14
MaxHeapify(A, 2)

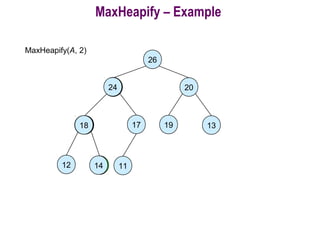
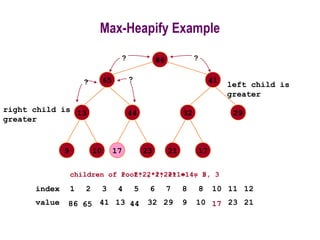
32. Running Time for MaxHeapify
Time to fix node i
and its children =
Θ(1)
Time to fix the
subtree rooted at
one of i’s children =
T(size of subree at
largest)
PLUS
MaxHeapify(A, i)
1. l = left(i);
2. r = right(i);
3. if (l ≤ heap-size[A] && A[l] > A[i])
4. largest = l;
5. else largest = I;
6. if (r ≤ heap-size[A] && A[r] > A[largest])
7. largest = r;
8. if (largest != i)
9. Swap(A[i], A[largest])
10. MaxHeapify(A, largest)
MaxHeapify(A, i)
1. l = left(i);
2. r = right(i);
3. if (l ≤ heap-size[A] && A[l] > A[i])
4. largest = l;
5. else largest = I;
6. if (r ≤ heap-size[A] && A[r] > A[largest])
7. largest = r;
8. if (largest != i)
9. Swap(A[i], A[largest])
10. MaxHeapify(A, largest)

33. Running Time for MaxHeapify(A, n)
T(n) = T(largest) + Θ(1)
largest ≤ 2n/3 (worst case occurs when the last
row of tree is exactly half full)
T(n) ≤ T(2n/3) + Θ(1) ⇒ T(n) = O(lg n)
Alternately, MaxHeapify takes O(h) where h is
the height of the node where MaxHeapify is
applied.

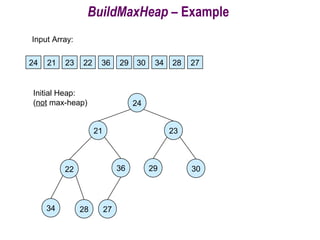
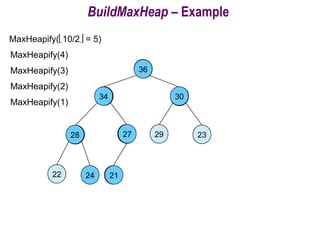
34. Building a heap
Use MaxHeapify to convert an array A into a max-heap.
How?
Call MaxHeapify on each element in a bottom-up
manner.
BuildMaxHeap(A)
1. heap-size[A] = length[A]
2. for i = length[A]/2 down to 1
3. do MaxHeapify(A, i)
BuildMaxHeap(A)
1. heap-size[A] = length[A]
2. for i = length[A]/2 down to 1
3. do MaxHeapify(A, i)

35. BuildMaxHeap – Example
24 21 23 22 36 29 30 34 28 27
Input Array:
24
21 23
22 36 29 30
34 28 27
Initial Heap:
(not max-heap)

36. BuildMaxHeap – Example
24
21 23
22 36 29 30
34 28 27
MaxHeapify(10/2 = 5)
3636
MaxHeapify(4)
2234
22
MaxHeapify(3)
2330
23
MaxHeapify(2)
2136
21
MaxHeapify(1)
2436
2434
2428
24
21
21
27

37. Running Time of BuildMaxHeap
Cost of a MaxHeapify call × No. of calls to MaxHeapify
O(lg n) × O(n) = O(nlg n)
BuildMaxHeap(A)
1. heap-size[A] = length[A]
2. for i = length[A]/2 down to 1
3. do MaxHeapify(A, i)
BuildMaxHeap(A)
1. heap-size[A] = length[A]
2. for i = length[A]/2 down to 1
3. do MaxHeapify(A, i) Θ(logn) Θ(n logn)

38. Heapsort
Goal:
Sort an array using heap representations
Idea:
Build a max-heap from the array
Swap the root (the maximum element) with the last element in the
array
“Discard” this last node by decreasing the heap size
Call MAX-HEAPIFY on the new root
Repeat this process until only one node remains

39. Example: A=[7, 4, 3, 1, 2]
MAX-HEAPIFY(A, 1, 4) MAX-HEAPIFY(A, 1, 3) MAX-HEAPIFY(A, 1, 2)
MAX-HEAPIFY(A, 1, 1)

40. Heapsort(A)
HeapSort(A)
1. Build-Max-Heap(A)
2. for i = length[A] downto 2
3. swap( A[1], A[i] );
4. heap-size[A] = heap-size[A] – 1;
5. MaxHeapify(A, 1);
HeapSort(A)
1. Build-Max-Heap(A)
2. for i = length[A] downto 2
3. swap( A[1], A[i] );
4. heap-size[A] = heap-size[A] – 1;
5. MaxHeapify(A, 1);

41. Algorithm Analysis
In-place
Not Stable
Build-Max-Heap takes O(n) and each of the n-1 calls to Max-Heapify
HeapSort(A)
1. Build-Max-Heap(A)
2. for i = length[A] downto 2
3. swap( A[1], A[i] );
4. heap-size[A] = heap-size[A] – 1;
5. MaxHeapify(A, 1);
HeapSort(A)
1. Build-Max-Heap(A)
2. for i = length[A] downto 2
3. swap( A[1], A[i] );
4. heap-size[A] = heap-size[A] – 1;
5. MaxHeapify(A, 1);
Θ(logn)
Θ(n)
Θ(n -1)
Θ(n logn)

42. delete
Last Node# 14 1110
25
2420
1815 716
8 9 10 11 12 16
22
3
7
3
25
3
24
22
3
3
16
25
Binary Heap: Delete /Extract Max

43. 43
Binary Heap: Delete /Extract Max

44. 44
Analysis Binary Heap: Delete /Extract Max
Θ(1)
Θ(logn)
Θ( logn)

45. 45
Binary Heap: Return/Find Max

46. 46
Analysis Binary Heap: Return/Find Max
Θ(1)
Θ(1)

47. 47
Binary Heap: Increase Key
The node i has its key increased to 15.

48. 48
Binary Heap: Increase Key

49. 49
Analysis Binary Heap: Increase Key
The running time of HEAP-INCREASE-KEY on an n-element
heap is O(lg n), since the path traced from the node to the
root has length O(lg n).

50. Binary Heap: Insertion
Insert element x into heap.
Insert into next available slot.
Bubble up until it's heap ordered.
– Peter principle: nodes rise to level of incompetence
98
84
78 68
51 4721
75
5367
4034 4933 89 next free slot

51. Binary Heap: Insertion
Insert element x into heap.
Insert into next available slot.
Bubble up until it's heap ordered.
– Peter principle: nodes rise to level of incompetence
98
84
78 68
51 4721
75
5367
4034 4933 4289
swap with parent

52. Binary Heap: Insertion
Insert element x into heap.
Insert into next available slot.
Bubble up until it's heap ordered.
– Peter principle: nodes rise to level of incompetence
swap with parent98
84
78 68
51 4721
75
8967
4034 4933 4253

53. Binary Heap: Insertion
Insert element x into heap.
Insert into next available slot.
Bubble up until it's heap ordered.
– Peter principle: nodes rise to level of incompetence
stop: heap ordered
O(log N)
operations.
98
84
78 68
51 4721
89
7567
4034 4933 4253

54. 54
Binary Heap: Insertion

55. 55
Analysis Binary Heap: Insertion
The running time of Insert on an n-element heap is O(lg n),
since the path traced from the node to the root has length
O(lg n).

56. Priority Queues
Build -heap
Operation
insert
find-min
delete-min
union
decrease-key
delete
N
log N
1
log N
N
log N
log N
is-empty 1