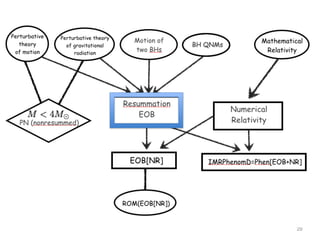
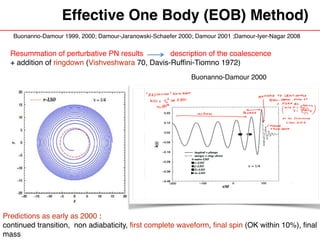
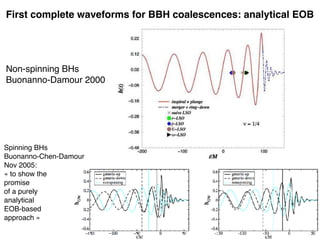
- The document discusses gravitational waves and binary systems, including perturbative computations of gravitational wave flux from binary systems up to order v7/c7. - It covers the effective one body (EOB) method for modeling binary coalescence, including resummations of post-Newtonian results and the addition of ringdown effects. This provides the first complete waveforms for binary black hole coalescences. 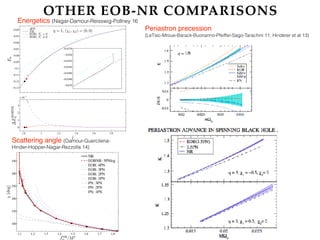- Developments are discussed such as extending EOB to include spinning bodies, comparisons to numerical relativity results, and using gravitational self-force calculations to improve EOB modeling.

1. GRAVITATIONAL WAVES
and
BINARY SYSTEMS (lecture 3)
Thibault Damour
Institut des Hautes Etudes Scientifiques
Waves on the lake: the astrophysics behind gravitational waves
Lake Como School of Advanced Studies - May 28 - June 1, 2018,
Como, Italy

2. 2-body Taylor-expanded 4PN Hamiltonian [DJS, 2014]
13

3. 3
Explicit Source Quadrupole Moment at 3.5 PN for a binary system
(Blanchet-Damour-Esposito-Farese-Iyer’05; Blanchet et al;Faye-Marsat-Blanchet-Iyer’12)

4. Perturbative computation of GW flux from binary system
• lowest order : Einstein 1918 Peters-Mathews 63
• 1 + (v2 /c2) : Wagoner-Will 76
• … + (v3 /c3) : Blanchet-Damour 92, Wiseman 93
• … + (v4 /c4) : Blanchet-Damour-Iyer Will-Wiseman 95
• … + (v5 /c5) : Blanchet 96
• … + (v6 /c6) : Blanchet-Damour-Esposito-Farèse-Iyer 2004
• … + (v7 /c7) : Blanchet
x =
⇣v
c
⌘2
=
✓
G(m1 + m2)⌦
c3
◆2
3
=
✓
⇡G(m1 + m2)f
c3
◆2
3
⌫ =
m1m2
(m1 + m2)2

5. 29

6. Effective One Body (EOB) Method)
Buonanno-Damour 1999, 2000; Damour-Jaranowski-Schaefer 2000; Damour 2001 ;Damour-Iyer-Nagar 2008
Predictions as early as 2000 :
continued transition, non adiabaticity, first complete waveform, final spin (OK within 10%), final
mass
Resummation of perturbative PN results description of the coalescence
+ addition of ringdown (Vishveshwara 70, Davis-Ruffini-Tiomno 1972)
Buonanno-Damour 2000

7. First complete waveforms for BBH coalescences: analytical EOB
Non-spinning BHs
Buonanno-Damour 2000
Spinning BHs
Buonanno-Chen-Damour
Nov 2005:
« to show the
promise
of a purely
analytical
EOB-based
approach »

8. EOB THEORY + EOB[NR] + EOB[SF] DEVELOPMENTS
8
Buonanno,Damour 99 (2 PN Hamiltonian)
Buonanno,Damour 00 (Rad.Reac. full waveform)
Damour, Jaranowski,Schäfer 00 (3 PN Hamiltonian)
Damour 01, (spinning bodies)
Buonanno, Chen, Damour 05,
Damour-Jaranowski,Schäfer 08, Barausse, Buonanno, 10, Nagar 11,
Balmelli-Jetzer 12, Taracchini et al 12,14, Damour,Nagar 14
Damour, Nagar 07, (factorized waveform)
Damour, Iyer, Nagar 08,
Pan et al. 11
Damour, Nagar 10 (BNS tidal effects)
Bini-Damour-Faye 12
Bini, Damour 13, Damour, Jaranowski, Schäfer 15 (4 PN Hamiltonian)
EOB vs NR and EOB[NR]
Buonanno, Cook, Pretorius 07,
Buonanno, Pan, Taracchini 08-
Damour-Nagar 08-
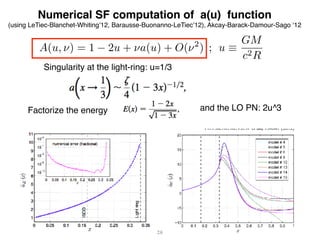
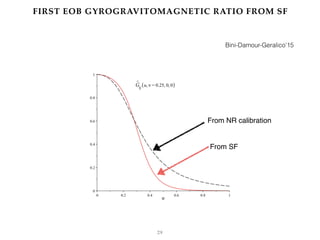
EOB vs SF and EOB[SF]
Damour 09
Barack-Sago-Damour 10
Barausse-Buonanno-LeTiec 12
Akcay-Barack-Damour-Sago 12
Bini-Damour 13-16
LeTiec 15
Bini-Damour-Geralico 16
Hopper-Kavanagh-Ottewill 16
Akcay-vandeMeent 16
Reduced Order Model version (Pürrer 2014, 2016) of
EOB[NR] (Taracchini et al 2014)
Phenomenological model (Ajith et al 2007, Hannam et
al 2014, Husa et al 2016, Kahn et al 2016)
of FFT of hybrids EOB + NR
EOB vs PM
Damour 16

9. EOB: resumming the dynamics of a two-body system (m_1,m_2,S_1,S_2)
in terms of the dynamics of a particle of mass mu and spin S*
moving in some effective metric g(M,S)
Effective metric for non-spinning bodies: a nu-deformation of Schwarzschild
ds2
e↵ = A(r; ⌫) dt2
+ B(r; ⌫) dr2
+ r2
d✓2
+ sin2
✓ d'2
µ =
m1m2
m1 + m2
M = m1 + m2 ⌫ =
µ
M
=
m1m2
(m1 + m2)2

10. Real dynamics versus Effective dynamics
G G2
1 loop
G3
2 loops
G4
3 loops
Real dynamics Effective dynamics
Effective metric for non-spinning bodies: a nu-deformation of
Schwarzschild
31
⌫ =
m1m2
(m1 + m2)2
ds2
e↵ = A(r; ⌫) dt2
+ B(r; ⌫) dr2
+ r2
d✓2
+ sin2
✓ d'2

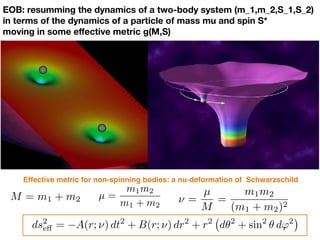
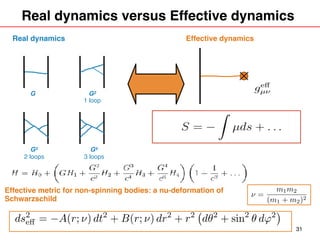
11. TWO-BODY/EOB “CORRESPONDENCE”:
THINK QUANTUM-MECHANICALLY (J.A. WHEELER)
11
1:1 map
(m1, m2)
µ =
m1m2
m1 + m2
ge
µ⇥
Bohr-Sommerfeld’s
Quantization Conditions
(action-angle variables &
Delaunay Hamiltonian)
J = ⌃ =
1
2
p d⇥
N = n = Ir + J
Ir =
1
2
prdr
Real 2-body system
(in the c.o.m. frame)
An effective particle
in some effective metric
Hclassical
(q, p) Equantum
(Ia = nah) = f 1[Equantum
e (Ie
a = nah)]
E = f(E)
Hclassical
(Ia)
µ2
+ gµ⇥
e
⇥Se
⇥xµ
⇥Se
⇥x⇥
+ O(p4
) = 0

12. 2-body Taylor-expanded N + 1PN + 2PN Hamiltonian
11

13. 13
Technical aspects of EOB
After going to the c.m. frame (p_1=-p_2=p) look for a canonical transformation G(q,p’)
Parametrizing a general energy-map:
System of algebraic eqs for unknown coefficients; impose b1=2

14. 14
EOB results at 1PN and 2PN

15. 2-body Taylor-expanded 3PN Hamiltonian [JS 98, DJS 01]
12

16. 16
EOB results at 3PN (DJS’00)
Less eqs than unknowns ? Need to introduce higher-in-momenta contributions
post-geodesic effective mass-shell condition
at 3PN
DJS gauge: z1=z2=0 to have only pr^4 terms

17. 17
3PN EOB

18. 2-body Taylor-expanded 4PN Hamiltonian [DJS, 2014]
13

19. Resummed (non-spinning) 4PN EOB interaction potentials
ds2
e↵ = A(r; ⌫) dt2
+ B(r; ⌫) dr2
+ r2
d✓2
+ sin2
✓ d'2 ¯D ⌘ (A B) 1
u ⌘
GM
R c2
AEOB
(u) = Pade1
4[AP N
(u)]

20. 20
Spinning EOB effective Hamiltonian
He↵ = Horb + Hso
S = S1 + S2 ; S⇤ =
m2
m1
S1 +
m1
m2
S2 ,
r3
GPN
S = 2
5
8
⌫u
27
8
⌫p2
r + ⌫
✓
51
4
u2 21
2
up2
r +
5
8
p4
r
◆
+ ⌫2
✓
1
8
u2
+
23
8
up2
r +
35
8
p4
r
◆
r3
GPN
S⇤
=
3
2
9
8
u
15
8
p2
r + ⌫
✓
3
4
u
9
4
p2
r
◆
27
16
u2
+
69
16
up2
r +
35
16
p4
r + ⌫
✓
39
4
u2 9
4
up2
r +
5
2
p4
r
◆
+⌫2
✓
3
16
u2
+
57
16
up2
r +
45
16
p4
r
◆
Gyrogravitomagnetic ratios (when neglecting spin^2 effects)
! HEOB = Mc2
s
1 + 2⌫
✓
He↵
µc2
1
◆
Damour’01, Damour-Jaranowski-Schaefer’08,Barausse-Buonanno’10, Damour-Nagar’14, ……

21. Resummed EOB waveform
(Damour-Iyer-Sathyaprakash ’98) Damour-Nagar ’07, Damour-Iyer -Nagar ’08, Pan et al. ‘10
NB: T_lm
resums an
infinite number
of terms and
already contains,
eg, 4.5PN tail^3
terms
(Messina-Nagar17)

22. STRUCTURE OF THE EOB FORMALISM
EOB Hamiltonian
Resummed (BD99)
PN dynamics
(DD81,D82,DJS01,IF03,BDIF04
)
EOB Rad. Reac. force
ˆFHEOB
Factorized waveform
h⇧m = h
(N,⇥)
⇧m
ˆh
(⇥)
⇧m
ˆh
(⇥)
⇧m = ˆS
(⇥)
eff T⇧mei m ⇧
⇧m
Resummed (DN07,DIN08)Resummed (DIS98)
BH perturbations
RW57, Z70, Z72
hEOB
m = (tm t)hinsplunge
m (t) + (t tm)hringdown
m (t)
hringdown
⇤m (t) =
N
C+
N e
+
N (t tm)
EOB waveform
PN waveform
BD89, B95&05,ABIQ04,
PN rad losses
WW76, BDIWW95, BDEFI
05
Matching at merger time
⇥N = N + i⇤N
QNMs spectrum
BNS: tides
(Love numbers)
22

23. OTHER EOB-NR COMPARISONS
23
Periastron precession
(LeTiec-Mroue-Barack-Buonanno-Pfeiffer-Sago-Tarachini 11, Hinderer et al 13)
−0.13
−0.12
−0.11
−0.1
−0.09
−0.08
−0.07
−0.06
−0.05
−0.04
Eb
4PN
NR
EOB, Fr = 0
EOB, Fr ̸= 0
2.8 3 3.2 3.4 3.6 3.8
0
1
2
3
x 10
−3
j
∆EEOBNR
b
−0.039
−0.0388
−0.0386
−0.0384
−0.0382
−0.038
−0.0378
q = 1, (χ1, χ2) = (0, 0)
Energetics (Nagar-Damour-Reisswig-Pollney 16
Scattering angle (Damour-Guercilena-
Hinder-Hopper-Nagar-Rezzolla 14)

24. EOB AND GSF
24
Comparable-mass case:
Gravitational Self-Force Theory : m1 << m2
• Analytical high-PN results : Blanchet-Detweiler-LeTiec-Whiting ’10,
Damour ’10, Blanchet et al ’10, LeTiec et al ’12, Bini-Damour ’13-15,
Kavanagh-Ottewill-Wardell ’15
• (gauge-invariant) Numerical results : Detweiler ’08, Barack-Sago ’09,
Blanchet-Detweiler-LeTiec-Whiting ’10, Barack-Damour-Sago ’10, Shah-
Friedman-Keidl ’12, Dolan et al ’14, Nolan et al ’15, …
• Analytical PN results from high-precision (hundreds to thousands of
digits !) numerical results : Shah-Friedman-Whiting ’14, Johnson-McDaniel-
Shah-Whiting ’15
m1 ⇠ m2
Bini-Damour-Geralico’16, Hopper-Kavanagh-Ottewill’16
Akcay-van de Meent ‘16

25. 25
Gravitational Self-Force
Black-Hole perturbation theory `a la Regge-Wheeler-Zerilli-Mano-Suzuki-Takasugi

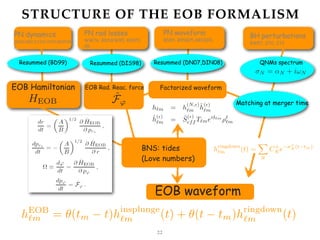
26. EOB, SF, EOB[SF], LISA ETC
26
Remarkable cancellations in EOB expansions in nu=m1m2/(m1+m2)^2: while
EOB[SF] program: improve the few EOB gauge-invariant potentials by SF-computing
(analytically or numerically) the contributions linear in nu. Recently implemented for
A, B, Q, gS, gS* (Bini,Damour,Geralico,Kavanagh,Akcay, van de Meent, Hopper,Wardell,Ottewill,…
Computation of 4PN O(nu) term in A from numerical (Barausse-Buonanno-LeTiec’12)
and analytical (Bini-Damour’13) SF computation;
Confirmation of all 4PN O(nu) terms of Damour-Jaranowski-Schaefer’14’15 from SF
computations (Barack-Damour-Sago, Bini-Damour-Geralico, van de Meent)
Aim: define template banks for LISA

27. GSF : ANALYTICAL HIGH-PN RESULTS
27
Bini-Damour 15 Kavanagh et al 15

28. 28
Numerical SF computation of a(u) function
(using LeTiec-Blanchet-Whiting’12, Barausse-Buonanno-LeTiec’12), Akcay-Barack-Damour-Sago ‘12
A(u, ⌫) = 1 2u + ⌫a(u) + O(⌫2
) ; u ⌘
GM
c2R
Singularity at the light-ring: u=1/3
Factorize the energy and the LO PN: 2u^3

29. FIRST EOB GYROGRAVITOMAGNETIC RATIO FROM SF
29
Bini-Damour-Geralico’15
From NR calibration
From SF