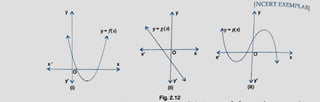
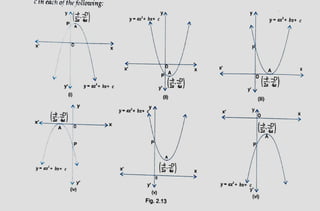
The document discusses various aspects of polynomials, including their graphs and properties, specifically focusing on quadratics and binomials. It poses several mathematical problems involving finding zeros, analyzing relationships between zeros and coefficients, and interpreting the behavior of polynomial functions. The content emphasizes the importance of understanding these relationships in the study of algebra.

1. foynomials (Grade o) (RAS) (,)
Aaw the arath of the tbonamial )e 2z
Alno,ind the Coordinaten_of theport nhe
þataboa
clacsmate
2)Aaw the grah of the fatynGrial f)a
3Aras the gaph of the auadrat paynsia
Date
4)Aaw the qoph of the baynamial S)=x6x+
S)ATa the qrah of thebonmial )
-4 t4x-A. AleO,d thhe Netex
8)TA each
)Araw the qraph t thebsynamial f)a
2?-4xt 5..
hicthone
the falauring grah in the
graph of a foty
faynamial, then identity rhieh
comohando toa
Coeahando to a auodrohe þounomial?

2. X
y'
()
y-f() yg()
(W)
Fig. 2.12
X
(H)
[NCERT EXEMPLARI
X

3. are qven in below

4. In each of the following:
x.
A
y
y= a+ bx+ c
0)
(iv)
y ar+ bx+ c
X
y= ax+ bx+ c
y ax+ bx+
y'
(v)
Fig. 2.13
A
X
X
y
y ar+ bx+ c
P
y
P
(1)
(v)
y= ax+ br+ c

5. 1o) Fnd the 2eras at theauadrate patynamial x't+1R,
and veriy the latn between the 2eros and its
loatgioents.
ie

6. I)ind he 2utoS. of the quadatie ktynomial
#)a bz-3,andvurçu the relatianahi between
the zurs andts coetticAnts
Data
12) Hnd the 2oos of the botynamiad fl)a 4u
+8u,and veitu the relathionahi etween
the zes and its eoethients
a
Paga
3) Fnd a auadatie batunial eoch ith the
gren munbu as the um and roduct o its
2U05 Jakucive
15)T one
4) C the roduct of the 2etos of the koynaial
az-6z-6 is4kind the vae ota
-(K2) in nucitrocal it she other,than fnd
he value o .
t 6a is recbrocal ot the othet, hnd the
Nae o a
o&
)rd the zeroS of the bsunsmialax-R
and veity the nelation etwean tthe enetiurds
and enos f the potynamiak.
18)ind the 2eras ot th paynamialt)
43+5x-23, and veity the latignahi
hatuseen the 2eroA and its coahfcunts
a) Find the zeros ot the auadratieþoynamial
A) ab + (6-ac)z-be and venisy the
alahsnehih beten the ROS and its caetticints.
20) TÊ d and axe the zNOS Of the quadatie
bstuamial f)2z-þx tq, thenfnd the values

7. a) Fnd a quadrat'e þotynomial, the um and
product of nhose 2en0e0 aree a and -
reabechrey. Alao, ind its 2eroeo.
r this to be bossible
aA) TA d, ane the 2aros of the poynmia
f)22? +5x+ k satishuing the nelatim
a4Tt d and ae the z005
clAsSmute
29)
Date
Poge
aadatie oynmial mchose 2er05 ane
Yeeitocala of the zercoS of the þatynamial.
of the quodratie
otynamial f)e-x-2,find a potunarnual
adt1 and2pt4
nhose 2eob asre
25)TA d ad Rae the 20C0S ot the quadrahe
aunamial foabxte, than eaate i
T dand Bae
26)TA d and ßae the20s thepotynanal
4l)-Sztkjuch that d-BaAtind
hose 2et05 are Qdt 36 and 3t2B
the zerOS of the auadohe
botumial A)kxt 4x+4 such that B'=24
nd the valwe okk
2
the 2ess o& the quadathc
2a)Te d and ae the r0s of the auadathe
batnsmial fl) e3z-4at4yfon a quadate
potunomial nhose 24rOs ae and g².

8. find the vae
of k
auadate ponsmials)= 2-8x+k
in 0,
the sauare
of 2IOS
of he
Page
Dat
a l
a
ssmat
e
30TA Aum