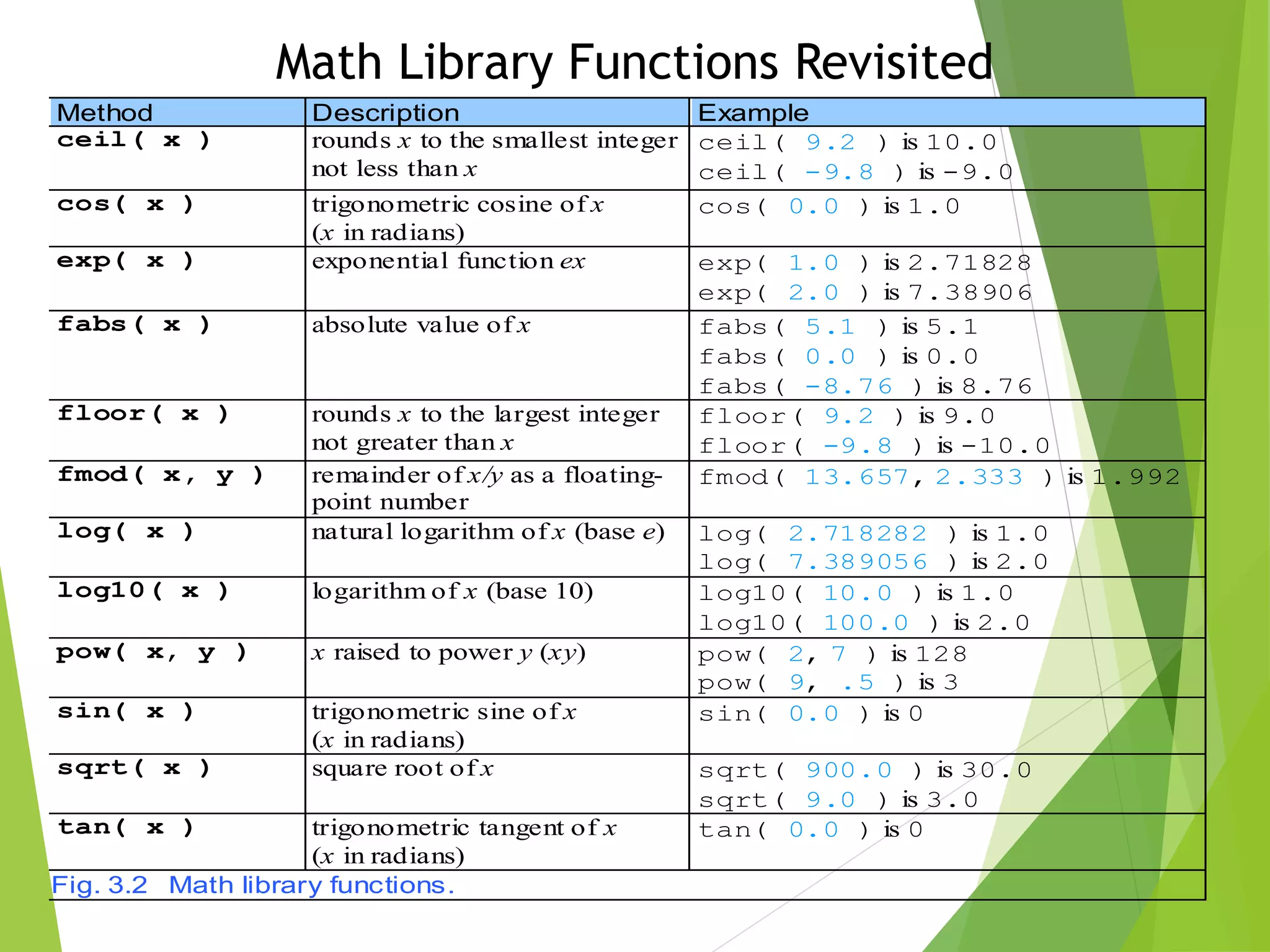
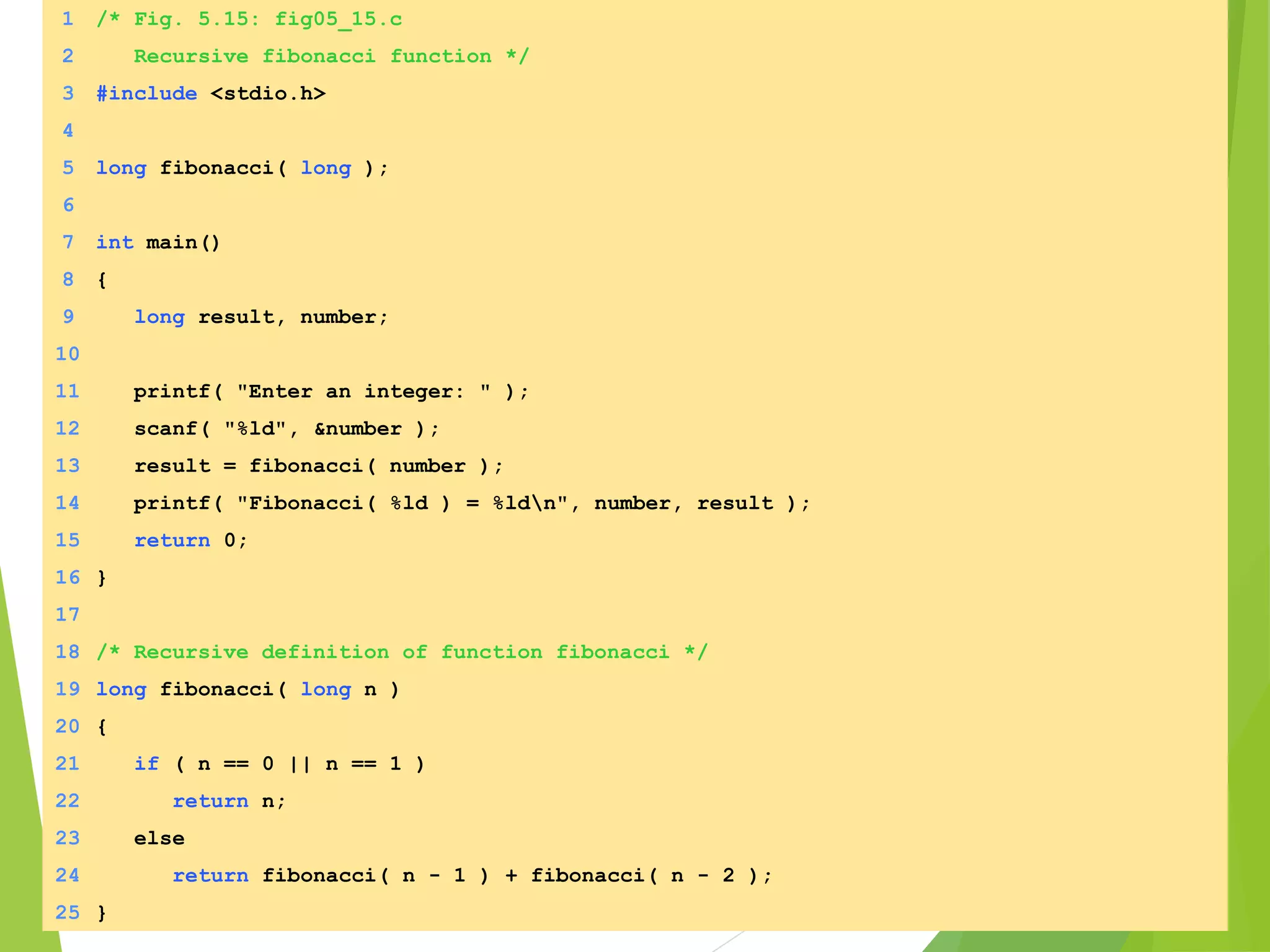
The document is a report on the topic of computer programming and utilization prepared by group C. It discusses functions, including the definition of a function, function examples, benefits of functions, function prototypes, function arguments, and recursion. It provides examples of math library functions, global and local variables, and external variables. It also includes examples of recursive functions to calculate factorials and the Fibonacci series recursively.