The document provides a detailed overview of Francis turbines, focusing on their main components, velocity triangles, and efficiency calculations. It discusses aspects such as velocity at different points, forces exerted by jets on the turbine buckets, and the work done by the jet on the runner. Additionally, it covers the definitions of hydraulic, mechanical, and overall efficiencies relevant to turbine performance.

1. Francis Turbine
Main Components
Velocity Triangle
Efficiencies
Design Aspects
Satish G. Taji
Assistant Professor
Civil Engineering Department
SRES’s Sanjivani College of Engineering, Kopargaon1
Hydraulic Turbines
1

2. Francis Turbine – Main Components
Prepared By Prof. S. G. Taji
Image Courtesy: Wikipedia (Google); gmdu.net (Google); pinterest (Google), learnengineering.org

3. Francis Turbine – Velocity Triangle
 R1, R2= Radius of wheel at the inlet and outlet of vanes
 V1, V2 = Absolute velocities of the jet at the inlet and
outlet respectively,
 u1, u2 = Peripheral velocities of the vane at the inlet
and outlet respectively,
 Vr1, Vr2 = Relative velocities at the inlet and outlet
respectively,
 Vf1, Vf2 = Velocities of the flow at the inlet and outlet
respectively,
 Vw1, Vw2 = Velocities of the whirl at inlet and outlet
 θ, φ = Tip angles at the inlet and outlet respectively,
 α, β = Angles made by absolute velocities at the inlet
and outlet
Prepared By Prof. S. G. Taji

4. Francis Turbine – Velocity Triangle
β < 90o
Prepared By Prof. S. G. Taji
Wheel
Tangent
at outlet
Tangent
at inlet
1
2
2
1
1
2

5. Francis Turbine – Velocity Triangle
β =90o
Prepared By Prof. S. G. Taji
Wheel
Tangent
at outlet
Tangent
at inlet

6. Francis Turbine – Velocity Triangle
β > 90o
Prepared By Prof. S. G. Taji
Wheel
Tangent
at outlet
Tangent
at inlet

7. Francis Turbine – Velocity Triangle
 Uniform velocity at inlet and outlet Tip (vane)
 u1 = π D1 N / 60
 u2 = π D2 N / 60
where, D1 =Dia. Of Wheel at the inlet
D2 =Dia. Of Wheel at the outlet;
N= Speed in rpm = 60f/p
 Force exerted by Jet on the Bucket (β<90O )
 Force exerted in the direction of motion
 Fx = Rate of Change of Momentum in the same dirn
But, in this case, momentum is angular momentum
∴ Fx= Mass of water striking the vane per second ×
(Initial angular momentum – final angular momentum)
Prepared By Prof. S. G. Taji
m
R
VM = m x v
Angular momentum
= (m x v) x R

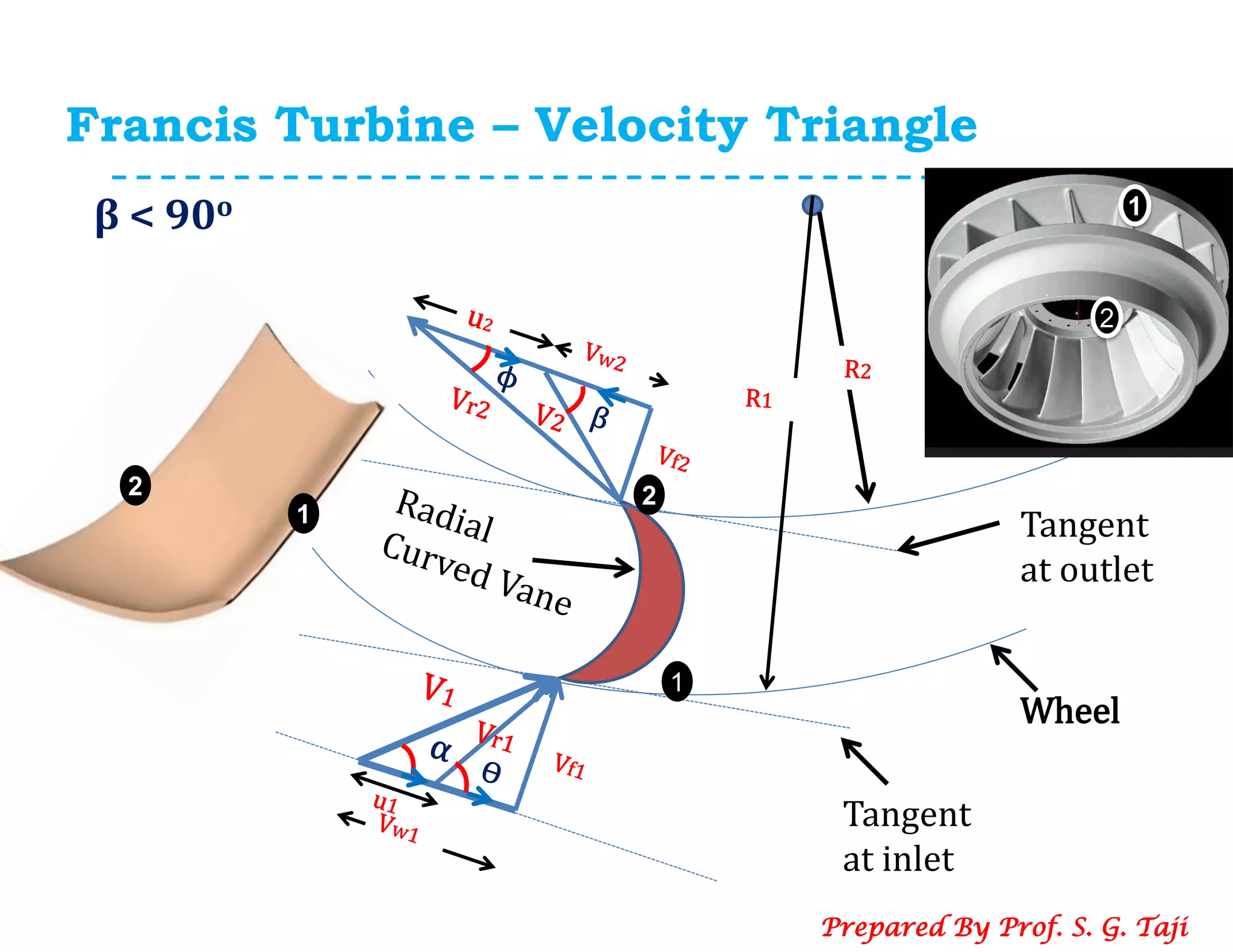
8. Francis Turbine – Velocity Triangle
 Force exerted by Jet on the Bucket (β<90O )
 Now, Angular Momentum = Momentum x Radius
i. momentum /sec at the inlet = (mass/sec) x (velocity
component in tangential dirn)
= (ρ a V1) x [Vw1]
ii. momentum /sec at the outlet= (mass/sec) x (velocity
component in tangential dirn)
= (ρ a V1) x [-Vw2]
iii. Angular momentum at inlet = (ρ a V1) x [Vw1] x R1
iv. Angular momentum at outlet = (ρ a V1) x [-Vw2] x R2
Prepared By Prof. S. G. Taji

9. Francis Turbine – Velocity Triangle
 Force exerted by Jet on the Bucket (β<90O )
∴ Fx= Mass of water striking the vane per second ×
(Initial angular momentum – final angular momentum)
Fx = (ρ a V1) x [Vw1 R1] - (ρ a V1) x [-Vw2] x R2
= (ρ a V1) [Vw1 R1 + Vw2 R2]
 When, β > 90o  Fx (ρ a V1) [Vw1 R1 - Vw2 R2]
 In general,
Fx = = (ρ a V1) [Vw1 R1 ± Vw2 R2]
 When, β = 90o (Radial discharge at outlet )
Fx = = (ρ a V1) [Vw1 R1]
Prepared By Prof. S. G. Taji

10. Francis Turbine – Velocity Triangle
 Work Done by Jet on the runner / sec
Work Done /sec = Fx x Angular Velocity (ω)
= (ρ a V1) x [Vw1 R1 ± Vw2R2] x ω
= (ρ a V1) x [Vw1 ω R1 ± Vw2 ω R2]
but, u1 = ωR1 & u2 = ωR2
Work Done /sec = (ρ a V1) x [Vw1 u1 ± Vw2 u2] N-m/s
Power = (ρ a V1) x [Vw1 u1 ± Vw2 u2] N-m/s or watts
 When, β = 90o (Radial discharge at outlet )
Work Done /sec = (ρ a V1) x [Vw1 u1]
Prepared By Prof. S. G. Taji

11. Francis Turbine – Efficiencies
 Hydraulic Efficiency (ήh)
 ήh = (WD/sec) / (KE/sec) OR RP / WP
Prepared By Prof. S. G. Taji

12. Francis Turbine – Efficiencies
 Mechanical Efficiency (ήm)
 ήm = (Shaft Power) / (WD/sec) OR SP / RP
 Overall Efficiency (ή0)
Prepared By Prof. S. G. Taji

13. Francis Turbine – Design Aspects
1. Discharge through reaction Turbine
Prepared By Prof. S. G. Taji

14. Francis Turbine – Design Aspects
2. Speed Ratio (Ku):
3. Flow Ratio (Kf):
4. Ratio of Width to Diameter (n)
Prepared By Prof. S. G. Taji