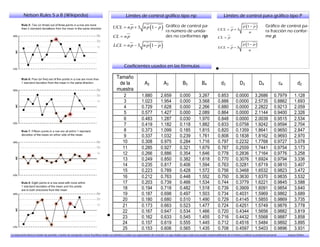
El documento detalla las reglas de Nelson para el control estadístico de procesos, incluyendo gráficos de control y límites. Se explican diferentes gráficas como las de medias, desviaciones estándar y proporciones, junto con sus respectivas fórmulas. Además, se enfatiza el papel de la educación en el desarrollo personal y la creatividad.

1. Nelson rules 1 a 4 (Wikipedia) Límites de control para gráficos xs
Gráfico de control para medias y desviaciones estándar.
Fórmulas y tablas
SPC (CEP)
Es similar al de medias y rangos. El nombre nos indica la
diferencia; se utiliza la desviación estándar en lugar del
rango para cuantificar la dispersión de los datos. G. Edgar Mata Ortiz http://licmata-math.blogspot.mx/
http://www.slideshare.net/licmata/
UCL  B4 s UCL  x  A3 s
Gráficos de control
CL  s CL  x Según Shewhart, son tres los pasos para el control estadísti-
co del proceso:
LCL  B3 s LCL  x  A3 s 1. Especificar qué es lo que se desea.
2. La producción de los objetos para cumplir con las especi-
Límites de control para gráficos C y U ficaciones y
3. Inspeccionar los objetos producidos para ver si cumplen
Gráfico de control para con lo especificado.
UCL  c  3 c número de no conformi- Los gráficos de control proporcionan un criterio para detec-
dades c. tar la pérdida de control estadístico de un proceso., es decir,
CL  c cuando la variabilidad del proceso es mayor o presenta
regularidades que no pueden ser atribuidas a cambios alea-
torios.
LCL  c  3 c
Gráfico de control para Límites de control para gráficos xR.
u
número de no conformi- UCL  u  3
dades por unidad u. n Gráfico de control para medias y rangos.
CL  u Está formado por dos gráficos colocados uno encima del
otro de forma tal que es posible visualizar tanto la media
u como el rango de cada conjunto de datos observados.
LCL  u  3
n
Referencias bibliográficas UCL  x  A2 R
Manual on presentation of data and control chart analysis. Com-
mittee E-11 on Statistical control. ASTM International. 1995. CL  x
Statistical models and control charts for high quality processess.
Min Xie, Thong Nigee Goh, Vellaismy Kuralmani. Springer. 2002. LCL  x  A2 R
Statistical method from the viewpoint of quality control. Walter A.
Shewhart edited by W. Edwards Deming. Dover publications.
1986.
UCL  D4 R
CL  R
LCL  D3 R
La educación tiene la misión de permitir, a todos sin excepción, hacer fructificar todos sus talentos y todas sus capacidades de creación. Lo que implica que cada uno pueda responsabilizarse de sí mismo y realizar su proyecto personal. Jaques Delors.

2. Nelson Rules 5 a 8 (Wikipedia) Límites de control gráfico tipo np Límites de control para gráfico tipo P
UCL  n p  3 n p 1  p   Gráfico de control pa-
ra número de unida- UCL  p  3

p 1 p  Gráfico de control pa-
ra fracción no confor-
n
CL  n p des no conformes np. CL  p me p.
LCL  n p  3 n p 1  p   LCL  p  3

p 1 p
n

Coeficientes usados en las fórmulas
Tamaño
de la A2 A3 B3 B4 d3 D3 D4 c4 d2
muestra
2 1.880 2.659 0.000 3.267 0.853 0.0000 3.2686 0.7979 1.128
3 1.023 1.954 0.000 3.568 0.888 0.0000 2.5735 0.8862 1.693
4 0.729 1.628 0.000 2.266 0.880 0.0000 2.2822 0.9213 2.059
5 0.577 1.427 0.000 2.089 0.864 0.0000 2.1144 0.9400 2.326
6 0.483 1.287 0.030 1.970 0.848 0.0000 2.0039 0.9515 2.534
7 0.419 1.182 0.118 1.882 0.833 0.0758 1.9242 0.9594 2.704
8 0.373 1.099 0.185 1.815 0.820 0.1359 1.8641 0.9650 2.847
9 0.337 1.032 0.239 1.761 0.808 0.1838 1.8162 0.9693 2.970
10 0.308 0.975 0.284 1.716 0.797 0.2232 1.7768 0.9727 3.078
11 0.285 0.927 0.321 1.679 0.787 0.2559 1.7441 0.9754 3.173
12 0.266 0.886 0.354 1.646 0.778 0.2836 1.7164 0.9776 3.258
13 0.249 0.850 0.382 1.618 0.770 0.3076 1.6924 0.9794 3.336
14 0.235 0.817 0.406 1.594 0.763 0.3281 1.6719 0.9810 3.407
15 0.223 0.789 0.428 1.572 0.756 0.3468 1.6532 0.9823 3.472
16 0.212 0.763 0.448 1.552 0.750 0.3630 1.6370 0.9835 3.532
17 0.203 0.739 0.466 1.534 0.744 0.3779 1.6221 0.9845 3.588
18 0.194 0.718 0.482 1.518 0.739 0.3909 1.6091 0.9854 3.640
19 0.187 0.698 0.497 1.503 0.734 0.4031 1.5969 0.9862 3.689
20 0.180 0.680 0.510 1.490 0.729 0.4145 1.5855 0.9869 3.735
21 0.173 0.663 0.523 1.477 0.724 0.4251 1.5749 0.9876 3.778
22 0.167 0.647 0.534 1.466 0.720 0.4344 1.5656 0.9882 3.819
23 0.162 0.633 0.545 1.455 0.716 0.4432 1.5568 0.9887 3.858
24 0.157 0.619 0.555 1.445 0.712 0.4516 1.5484 0.9892 3.895
25 0.153 0.606 0.565 1.435 0.708 0.4597 1.5403 0.9896 3.931
La educación tiene la misión de permitir, a todos sin excepción, hacer fructificar todos sus talentos y todas sus capacidades de creación. Lo que implica que cada uno pueda responsabilizarse de sí mismo y realizar su proyecto personal. Jaques Delors.