Excel curs-1

Lucrul în mediul Excel

CAPITOLUL 1
LUCRUL ÎN MEDIUL EXCEL
1.1. Componentele ferestrei Excel
Fereastra Excel – figura 1.1.- are numeroase elemente comune cu ferestrele Windows:
• o bar[ de meniuri - de unde se pot selecta comenzi;
• o bar[ de stare – care indic[ starea activit[ii curente;
• bare de instrumente – care conin butoane =i liste derulante prin care se obine acces rapid
la comenzile utilizate rapid.
Bara de meniuri

Celul[

Bara de stare

Bare de instrumente

Suprafaa foii de calcul
Figura 1.1 – fereastra Excel

}n plus, o fereastr[ Excel conine c`teva elemente unice, care vor fi explicate pe
parcursul leciei.

Modelarea deciziilor utilizând foile de calcul

1.2. Configurarea unui nou registru de calcul
C`nd se lanseaz[ ]n execuie programul Excel, pe ecran apare o fereastr[ care conine
un registru de calcul nou. Registrul (Workbook) este principalul document folosit ]n Excel
pentru stocarea =i prelucrarea datelor. Un registru este format din foi de calcul individuale,
fiecare din acestea put`nd conine date. }n configuraia prestabilit[, fiecare registru de calcul
creat conine 3 foi de calcul (Sheet1, Sheet2, Sheet3), dar ulterior se pot ad[uga mai multe
foi (p`n[ la 255).
Foile de calcul pot conine diverse tipuri de informaii. }n mod obi=nuit foile dintr-un
registru de calcul conin informaii legate ]ntre ele. De exemplu, la un buget, fiecare foaie
poate conine bugetul pentru un anumit departament din cadrul companiei.
}n partea de jos a registrului exist[ o bar[ de derulare a foilor de calcul (figura 1.2). }n
aceast[ bar[ sunt afi=ate numele foilor de calcul. (Dac[ aceast[ bar[ nu apare, din meniul
Tools se selecteaz[ comanda Options. }n caseta de dialog Options se selecteaz[ butonul
View =i se marcheaz[ caseta Sheet Tools). La un registru nou, foaia de calcul curent[ este
Sheet1. Se poate trece la o alt[ foaie f[c`nd clic pe numele ei. De exemplu pentru a trece pe
foaia Sheet 2 se face clic pe deasupra numelui ei.

Etichetele foilor de calcul

Bara de derulare a foilor de calcul

Figura 1.2 – bara de derulare a foilor de calcul
}n bara de derulare a foilor de calcul, nu pot apare numele tuturor foilor de calcul. De
aceea, ]n bara de derulare a foilor au mai fost prev[zute 4 butoane care permit deplasarea
printre foile registrului. Aceste butoane nu realizeaz[ selectarea foilor de calcul, ele permit
doar derularea numelor lor.
Tabelul de mai jos descrie operaiile pe care le realizeaz[ aceste butoane:
Buton
<
>
<
>

Operaie
Deplasarea la prima foaie de calcul a registrului
Deplasarea la ultima foaie de calcul a registrului
Deplasarea spre st`nga cu o foaie
Deplasarea spre dreapta cu o foaie

Dac[ un registru conine mai multe foi de calcul, numele acestora sunt importante
pentru identificare. Chiar =i atunci c`nd exist[ o singur[ foaie ]n registrul de calcul, numele
acesteia este important, deoarece poate fi folosit ]n formule =i furnizeaz[ antetul prestabilit
pentru pagina tip[rit[. De aceea este recomandabil ca foilor de calcul s[ li se acorde nume
mai sugestive dec`t Sheet 1, Sheet2 etc.
Pentru a denumi o foaie de calcul se execut[ urm[torii pa=i:
1. Se aplic[ un dublu clic pe eticheta foii de calcul (]n bara de derulare a foilor de calcul).
Numele foii de calcul va fi afi=at ]n video invers;
2. Se introduce noul nume, dup[ care se apas[ <Enter>.
}n mod prestabilit un registru conine 3 foi de calcul. Dac[ este necesar se pot ad[uga
noi foi de calcul. Pentru a introduce o nou[ foaie de calcul trebuie parcur=i urm[torii pa=i:

1. Se poziioneaz[ cursorul mouse-ului pe eticheta unei foi de calcul (]n bara de derulare a
foilor de calcul);
2. Se aplic[ un clic folosind butonul drept al mouse-ului;
3. Pe ecran apare un meniu din care se selecteaz[ comanda Insert.
Foile de calcul suplimentare pot fi eliminate prin operaia de =tergere astfel:
1. Se poziioneaz[ cursorul mouse-ului pe eticheta unei foi de calcul (]n bara de derulare a
foilor de calcul);
2. Se aplic[ un clic folosind butonul drept al mouseului;
3. Pe ecran apare un meniu din care se selecteaz[ comanda Delete.

1.3. Deplasarea în cadrul foii de calcul
}ntr-o foaie de calcul informaiile sunt prezentate ]n cadrul unei interfee grafice
formate din linii =i coloane (figura 1.3). Coloanele au ata=ate litere, iar liniile sunt numerotate
cu cifre. O foaie de calcul conine 256 coloane =i 65536 de linii. Coloanele au etichetele
dispuse ]n partea superioar[ a ferestrei documentului =i sunt notate cu litere (A, B, ..., Z), apoi
combinaii de dou[ litere (AA, AB p`n[ la IV). Liniile sunt numerotate de la 1 la 65536 ]n
partea st`ng[ a ferestrei documentului.

etichetele coloanei

celula
activ[

etichetele liniei
Casete de
derulare
Bara de derulare
vericala

Figura 1.3

Bara de derulare
orizontal[

La intersecia dintre o coloan[ =i o linie se g[se=te o celul[. Celula este unitatea
fundamental[ pentru stocarea datelor. Ea poate fi referit[ folosind litera coloanei =i cifra liniei
la intersecia c[rora se afl[ (de exemplu A5, B7). }ntr-o celul[ se pot introduce mai multe
tipuri de informaii:
• Texte - capete de tabel, etichete, note, texte explicative;
• Valori – numere, date calendaristice =i ore, valori logice;
• Formule – formule de calcul cu ajutorul c[rora este calculat[ o nou[ valoare ]n funcie
de informaiile din alte celule.
Celula activ[ este celula care este marcat[. Informaiile tastate apar ]n celula activ[.
Pentru a introduce date ]n alt[ celul[, mai ]nt`i se activeaz[ celula respectiv[. Dup[
introducerea datelor se iese din celul[ cu <Enter>, altfel exist[ posibilitatea ca urm[toarele
comenzi s[ nu poat[ fi aplicate.

Foile de calcul pot avea uneori dimensiuni foarte mari. }n aceste situaii pentru a g[si
sau introduce informaii trebuie folosite metode speciale de deplasare prin foile de calcul.
Deplasarea se poate efectua cu mouse-ul sau prin intermediul tastaturii. Pentru a efectua
deplasarea (prin foaie) cu mouse-ul se folosesc barele de derulare vertical[ =i orizontal[ care
se g[sesc ]n partea dreapt[ =i de jos a fiec[rei foi de calcul (figura 1.3).
Fiecare bar[ conine dou[ s[gei. Prin executarea unui clic pe o s[geat[ se pot realiza
urm[toarele operaii:
5
Derulare o linie ]n sus
6
Derulare o linie ]n jos
3
Derulare o coloan[ la st`nga
4
Derulare o coloan[ la dreapta
Pentru deplasare mai rapid[ prin foaie se pot folosi casetele de derulare (prin tragerea
lor ]n bara de derulare). Locul ocupat de caseta de derulare ]n cadrul barei de derulare indic[
poziia relativ[ a ferestrei fa[ de ]ntreaga zon[ a foii de calcul.
O celul[ se poate activa rapid plas`nd cursorul mouse-ului pe celula respectiv[ =i
execut`nd un clic pe butonul din st`nga al mouse-ului.
Deplasarea prin foaia de calcul cu ajutorul tastaturii se poate face cu urm[toarele
taste:
Tast[

<Tab>
<Home>
<Ctrl>‡<Home>
<Ctrl>‡<End>
<Page Up>
<Page Down>
<Ctrl>‡<Page Up>
<Ctrl>‡<Page Down>

Aciune
Deplasare o celul[ la st`nga
Deplasare o celul[ la dreapta
Deplasare o celul[ ]n sus
Deplasare o celul[ ]n jos
Deplasare o celul[ la dreapta
Deplasare ]n celula din extrema
st`ng[ a unui r`nd
Deplasare ]n celula A1 a foii de
calcul
Deplasare ]n ultima celul[ folosit[
din foaia de calcul (colul din dreapta
jos)
Deplasare ]n sus cu un ecran
Deplasare ]n jos cu un ecran
Deplasare la dreapta cu un ecran
Deplasare la st`nga cu un ecran

1.4. Utilizarea barelor de instrumente
Barele de instrumente (afi=ate sub meniu) permit un acces mai rapid la procedurile =i
comenzile des utilizate. Pentru a lucra cu barele de instrumente este necesar mouse-ul. Pentru
utilizarea unei anumite comenzi se execut[ un clic pe butonul asociat comenzii sau funciei
de care avei nevoie.
}n Excel exist[ mai multe bare de instrumente, dar nu trebuie folosite toate ]n acela=i
timp deoarece se ]ncarc[ prea mult ecranul. Este bine s[ fie vizualizate doar barele care
conin comenzi ce trebuie folosite. Exist[ mai multe bare de instrumente predefinite care pot
fi afi=ate select`nd din meniul View comanda Toolbars. Cele mai folosite bare de
instrumente sunt prezentate ]n continuare:


Bara Standard.
Conine butoane pentru comenzi de formatare, administrare fi=iere =i tip[rire.

Bara Formatting
Conine butoane utilizate pentru formatarea fonturilor, comenzi de aliniere, formate
numerice, formatarea marginilor, stabilire culori.

Bara Chart.
Conine butoane pentru formatarea graficelor.

Bara Pivot Table
Conine butoane folosite pentru crearea, actualizarea =i organizarea tabelelor pivot

Bara Drawing.
Conine butoane pentru desenare.

Bara Forms.
Conine butoane prin intermediul c[rora se pot ad[uga foii de calcul obiecte cum ar fi:
casete de validare, butoane de opiuni, liste de derulare.

Bara Stop Recording.
Conine dou[ butone care produc ]ncheierea =i oprirea/repornirea ]nregistr[rii unei
comenzi macro.

Bara Audit.
Conine butoane cu comenzi pentru detectarea erorilor uzuale din foile de calcul
Excel.

Bara Full Screen.
Aceast[ bar[ de instrumente apare atunci c`nd Excel a fost configurat pentru lucrul pe
]ntreg ecranul. Ap[sarea butonului produce ]ntoarcerea la modul de lucru anterior.


1.5. Afişarea/ascunderea barelor de instrumente
Pentru a avea acces la alte comenzi sau pentru a m[ri spaiul de lucru, barele de
instrumente pot fi afi=ate sau ascunse.
Pa=ii care trebuiesc efectuai pentru afi=area/ascunderea barelor de instrumente sunt:
1. Se aplic[ comanda View, Toolbars, Customize.
2. Pe ecran este afi=at[ caseta de dialog Customize (figura 1.4) care este alc[tuit[ din trei
seciuni: Toolbars, Commands =i Options. Aceste seciuni sunt activate la ap[sarea
butoanelor corespunz[toare din partea superioar[ a ferestrei. Se selecteaz[ butonul
Toolbars.

Figura 1.4 – caseta de dialog Customize - seciunea Toolbars
3. În lista Toolbars sunt afi=ate numele tuturor barelor de instrumente din Excel. Vor fi
afi=ate numai barele de instrumente care sunt marcate. Marcarea/demarcarea se face
aplicând un clic în dreptul casetei din dreptul numelui barei.
4. Se aplic[ un clic pe butonul Close.

1.6. Adăugarea/ascunderea butoanelor dintr-o bară de instrumente
Componena unei bare de instrumente se poate modifica. Exist[ situaii în care la o
bar[ de instrumente trebuie ad[ugat un buton nou sau trebuie =ters un buton. Aceste
modific[ri se pot face în seciunea Commands a casetei Customize (figura 1.5).
Aceast[ seciune conine:
- lista Categories. În aceast[ list[ apar toate titlurile de meniuri verticale.
- lista Commands. La selectarea unui meniu din lista Categories, în lista Commands apar
toate comenzile care pot fi aplicate din meniul respectiv.


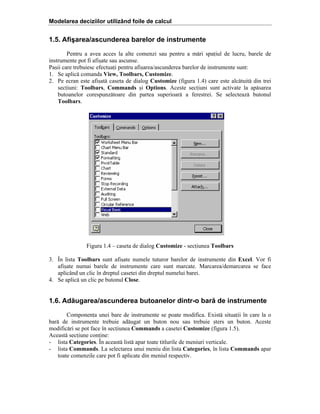
Figura 1.5 – fereastra de dialog Customize - seciunea Commands
Pentru a ad[uga un buton nou pe o bar[ de instrumente:
1. Se aplic[ comanda View, Toolbars, Customize
2. Se activeaz[ seciunea Commands, prin selectarea butonului Commands
3. Se selecteaz[ din lista Categories comanda asociat[ butonului
4. |inând butonul stânga al mouse-ului ap[sat, se trage mouse-ul în poziia în care trebuie
inserat butonul. În poziia în care butonul poate fi ad[ugat cursorul mouse-ului î=i
modific[ forma – apare un cursor în forma literei I
5. Se elibereaz[ butonul mouse-ului
6. Se selecteaz[ butonul Close
Pentru a =terge un buton de pe o bar[ de instrumente:
1. Se aplic[ comanda View, Toolbars, Customize
2. Se activeaz[ seciunea Commands, prin selectarea butonului Commands
3. Se aplic[ un clic pe butonul care trebuie =ters dintr-o bar[ de instrumente
4. |inând butonul stâng al mouse-ului ap[sat, se trage de mouse în interiorul casetei
Customize (în orice poziie !)
5. Se elibereaz[ butonul mouse-ului
6. Se selecteaz[ butonul Close
Pentru a reveni la structura standard a unei bare de instrumente, ]n seciunea Toolbars
a casetei de dialog Customize se selecteaz[ bara de instrumente respectiv[, se verific[ dac[
este marcat[ =i se aplic[ comanda Reset.
Este bine ca pentru ]nceput s[ fie afi=ate doar dou[ bare de instrumente: Standard =i
Formating.


1.7. Opţiuni suplimentare de afişare a butoanelor
Forma butoanelor din barele de instrumente poate fi stabilit[ în seciunea Options a
ferestrei Customize (figura 1.6).

Figura 1.6 - fereastra de dialog Customize - seciunea Options
Aceast[ seciune conine:
- opiunea Large Icons. Dac[ opiunea este marcat[, butoanele vor fi mari, dac[ nu este
marcat[ butoanele vor fi mici
- opiunea Show Screen Tips on toolbars. Screen Tips reprezint[ suprafaa mic[, de
culoare galben[, în care este afi=at numele butonului deasupra c[ruia este poziionat
cursorul mouse-ului. Dac[ opiunea este marcat[, numele butonului va fi afi=at, dac[ nu
este marcat[ numele butonului nu va fi afi=at. Recomand[m ca aceast[ opiune s[ fie
marcat[
- lista Menu animations. Din aceast[ list[ se selecteaz[ modul de deschidere a meniurilor.
Opiunile sunt:
• None
– modul normal de deschidere. Nu se aplic[ nici un efect
• Random – meniurile se deschid aleator (o parte oarecare mai întâi)
• Unfold
– modul de deschidere seam[n[ cu o desp[turire
• Slide
– deshiderea d[ senzaia de alunecare

Filtrarea datelor

CAPITOLUL 10
FILTRAREA DATELOR
10.1. Filtrarea datelor dintr-o listă
Filtrarea datelor dintr-o list[ este o operaie prin care sunt afi=ate doar acele ]nregistr[ri
din list[ care corespund unor criterii specificate =i ascunderea celorlalte ]nregistr[ri care nu
mai sunt afi=ate. }n Excel exist[ dou[ metode de filtrare: comanda Auto Filter pentru a
efectua o filtrare rapid[ a datelor din list[ =i comanda Advenced Filter pentru a filtra pe baza
unor criterii suplimentare.

10.2. Utilizarea comenzii Auto Filter
Comanda Auto Filter ofer[ o putere deosebit[ de gestionare a listelor. Informaiile care
nu trebuie vizualizate sau tip[rite pot fi filtrate rapid doar aplic`nd clicuri. Liniile de date
(]nregistr[rile) care nu ]ndeplinesc criteriile specificate sunt ascunse. Din aceast[ cauz[ atunci
c`nd se face o filtrare numerele de linie apar pe s[rite =i sunt afi=ate cu culoare albastr[.
Pentru a filtra o list[ cu comanda Auto Filter se execut[ urm[torii pa=i:
1. Se selecteaz[ o celul[ din lista ce trebuie filtrat[.
2. Din meniul Data se aplic[ comenziile Filter, Auto Filter.
Excel va insera s[gei de derulare ]n dreptul fiec[rei celule din capul de tabel.
3. Se aplic[ un clic pe s[geata de derulare din coloana ]n care se va introduce criteriul. Se
selecteaz[ criteriul pentru coloana respectiv[. Sunt posibile urm[toarele opiuni:
All
Permite afi=area tuturor ]nregistr[rilor cu acest c`mp.
(Top 10)
Permite selectarea unui subset de ]nregistr[ri pornind de sus sau de jos
]ntr-o list[. Se poate specifica fie num[rul de elemente, fie procentul de
elemente ce vor fi filtrate. La selectarea acestei opiuni apare caseta de
dialog Top 10 Autofilter (figura 10.1).

Figura 10.1 – caseta de dialog Top 10 Autofilter

Custom

Din prima list[ derulant[ se selecteaz[ Top /Bottom, ]n funcie de
direcia ]n care se va face filtrarea de sus (Top) sau de jos (Bottom).
}n a doua list[ derulant[ se introduce sau se selecteaz[ un num[r care
indic[ c`te ]nregistr[ri (dac[ ]n a treia list[ derulant[este selectat[
opiunea Items) sau ce procent din num[rul total de ]nregistr[ri (dac[
]n a treia list[ derulant[ este selectat[ opiunea Percent) vor rezulta
din filtrare.
Permite crearea unor criterii definite cu condiii =i/sau. La selectarea
acestei opiuni apare caseta de dialog Custom AutoFilter (figura
10.2).


Figura 10.2 – caseta de dialog Custom AutoFilter

4.

Pentru a introduce criterii comparative se selecteaz[ un operator din
prima list[ derulant[, apoi se introduce o valoare ]n caseta al[turat[.
Dac[ exist[ un al doilea criteriu se selecteaz[ una din opiunile AND
(=i) sau OR (sau) =i se introduce ]n mod similar al doilea criteriu.
Blanks
Afi=eaz[ toate ]nregistr[rile cu spaii ]n acest c`mp.
Non Blanks
Afi=eaz[ toate ]nregistr[rile care nu conin spaii ]n acest c`mp
(]nregistr[ri ce conin date).
}n plus apare o list[ cu toate valorile distincte din coloana curent[. La selectarea acestor
valori vor fi afi=ate doar ]nregistr[rile care au exact aceast[ valoare ]n c`mpul
specificat. Numele coloanelor dup[ care s-a f[cut filtrarea apar cu albastru.
Se aplic[ pa=ii 1-3 pentru a filtra datele =i ]n funcie de alte criterii. Pe m[sur[ ce se
selecteaz[ mai multe criterii ele sunt combinate =i cu criteriile anterioare. Pentru ca o
]nregistrare s[ fie afi=at[ ea trebuie s[ ]ndeplineasc[ criteriile pentru toate c`mpurile.

Dac[ trebuie anulat rezultatul filtr[rii dup[ un anumit c`mp se selecteaz[ s[geata de
derulare pentru acel c`mp =i se selecteaz[ opiunea All. Pentru a afi=a toate ]nregistr[rile =i a
]nl[tura criteriile din toate c`mpurile se aplic[ comanda Data, Filter, Show All. Atunci c`nd
comanda AutoFilter este activ[, ]n meniu, ]n dreptul comenzii apare un marcaj de validare.
Pentru a dezactiva aceast[ facilitate se aplic[ din nou comanda Data, Filter, AutoFilter.

10.3. Aplicaţie
Foaia de calcul urm[toare (figura 10.3) conine o list[ cu facturile emise de o firm[.
Pentru fiecare factur[ sunt specificate urm[toarele date:
• codul facturii
• data emiterii facturii
• numele distribuitorului
• numele clientului
• produs v`ndut
• preul unitar
• cantitatea v`ndut[
• valoarea total[ (preul unitar*cantitatea v`ndut[).
Pentru a calcula valoarea total[ se introduce ]n celula H2 formula =F2*G2. Aceast[
formul[ se va copia pe coloan[.
1. Se selecteaz[ o celul[ din list[.

Filtrarea datelor

Figura 10.3
2. Din meniul Data se aplic[ comanda Filter, Autofilter. }n dreptul fiec[rei celule
din capul de tabel se insereaz[ o s[geat[ de derulare.
Prin filtrare se poate r[spunde la ]ntreb[ri de genul: S[ se vizualizeze toate comenzile
livrate de Popescu.
Pentru aceasta se aplic[ un clic pe s[geata de derulare din coloana Distribuitor =i se
selecteaz[ din lista afi=at[ Popescu.
Dac[ trebuie vizualizate toate comenzile livrate de Popescu cu valoare mai mare de
500000 lei se mai face o filtrare dup[ c`mpul Total. Se aplic[ un clic pe s[geata de derulare
din coloana Total =i se selecteaz[ opiunea Custom. Din lista de operatori se selecteaz[
operatorul >, iar ]n caseta al[turat[ se introduce valoarea 500000. Se selecteaz[ butonul OK.

10.4. Utilizarea comenzii Advanced Filter
O alt[ metod[ de filtrare este folosirea comenzii Advanced Filter. Cu aceast[
comand[ se pot efectua operaii de filtrare bazate pe criterii complexe. Pentru folosirea
comenzii trebuie creat un domeniu de criterii. Domeniul de criterii specific[ condiiile pe care
datele filtrate trebuie s[ le ]ndeplineasc[. Prima linie din domeniul de criterii conine numele
c`mpurilor pentru care se vor specifica criterii. Numele c`mpurilor trebuie scrise exact la fel
ca numele c`mpurilor din list[. }n liniile imediat urm[toare, sub numele c`mpurilor, se
introduc criteriile pentru c`mpurile respective. Domeniul de criterii se va termina cu o linie
goal[. Criteriile care sunt pe aceea=i linie ]n domeniul de criterii vor trebui s[ fie ]ndeplinite
simultan. }ntre criteriile care se g[sesc pe linii diferite aplic[ o relaie de tip SAU.
Dup[ preg[tirea domeniului de criterii se execut[ urm[torii pa=i:
1. Se selecteaz[ domeniul de celule care conine lista
2. Se aplic[ comanda Data, Filter, Advanced Filter. Pe ecran apare caseta de dialog
Advanced Filter (figura 12.4):
3. Dac[ lista filtrat[ va fi afi=at[ ]n acela=i loc ca =i lista iniial[ se selecteaz[ opiunea Filter
the List, in place. Dac[ datele trebuie plasate ]ntr-o alt[ zon[ a foii de calcul pentru a fi
prelucrate ulterior se selecteaz[ opiunea Copy To Another Location. }n acest caz ]n
caseta Copy To se specific[ domeniul de celule ce va conine lista, dac[ acesta nu a
ap[rut automat.
4. }n caseta List Range se introduce domeniul de celule care conine lista, dac[ acesta nu a
ap[rut automat.


Figura 12.4 – caseta de dialog Advanced Filter
5. }n caseta Criteria Range se introduce domeniul de celule care conine domeniul de
criterii.
6. Dac[ prin filtrare trebuie ]nl[turate ]nregistr[rile duble se marcheaz[ opiunea Unique
Records Only.
7. Se selecteaz[ butonul OK.

10.5. Aplicaţie
}n exemplul din aplicaia precedent[ s[ se realizeze o filtrare astfel ]nc`t s[ fie
vizualizate doar comenzile ]n valoare de 500.000 de lei livrate de Popescu folosind comanda
Advanced Filter.

Figura 12.5
La sf`r=itul listei (figura 12.5) se las[ o linie liber[ =i se introduce domeniul de
criterii. Se vor introduce ]n foaia de calcul urm[toarele informaii:
}n A10
Distribuitor
}n B10
Val. Totala
}n A11
Popescu
}n B11
>500000
Rezolvare:
1. Se selecteaz[ domeniul de celule care conine lista A1:H8.
2. Se aplic[ comanda Data, Filter, Advanced Filter.
3. Caseta de dialog Advanced Filter se completeaz[ ]n modul urm[tor:
• se selecteaz[ opiunea Filter the List, in place
• List Range
A1:H8
• Criteria Range
A10:B11
• se demarcheaz[ opiunea Unique Records Only.

Compararea alternativelor in vederea luarii deciziei optime

CAPITOLUL 11
COMPARAREA ALTERNATIVELOR ÎN VEDEREA LUĂRII
DECIZIEI OPTIME
11.1. Utilizarea facilităţii Goal Seek
Excel dispune de o serie de facilit[i pentru a putea r[spunde la ]ntreb[ri de genul “Ce
se ]nt`mpl[ dac[ ?“. Presupunem c[ avem o foaie de calcul, cunoa=tem r[spunsul dorit, dar
vrem s[ rezolv[m problema =i ]n sens invers, adic[ s[ g[sim valoarea de intrare care conduce
la un anumit r[spuns. Pentru a putea rezolva probleme de acest tip se utilizeaz[ comanda
Goal Seek.
Pentru a folosi comanda Goal Seek se formuleaz[ ]nt`i problema, se introduc
variabilele =i formulele ]n foaia de calcul. Celula cu rezultate trebuie s[ conin[ neap[rat o
formul[, iar formula respectiv[ trebuie s[ conin[ referiri la alte celule din foaia de calcul,
celule care conin variabile de intrare.
Pentru g[sirea valorii de intrare care s[ conduc[ la un anumit r[spuns se vor parcurge
urm[toarele etape:
1. Se selecteaz[ celula rezultat, care trebuie s[ conin[ o formul[ =i ]n care vrem s[ obinem o
anumit[ valoare.
2. Se aplic[ comanda Tools, Goal Seek. Pe ecran apare caseta de dialog Goal Seek (figura
11.1).

Figura 11.1 – caseta de dialog Goal Seek
3. Caseta Set Cell conine celula selectat[ ]n etapa 1. Dac[ s-a s[rit peste etapa 1, se scrie ]n
aceast[ caset[ referina celulei rezultat. }n caseta To value se introduce soluia la care vrei
s[ ajungei. }n caseta By changing Cell se scrie referina celulei de intrare. Aceast[ celul[
trebuie s[ contribuie la valoarea formulei din celula rezultat, specificat[ ]n Set Cell.
Goal Seek ]nlocuie=te valoarea de intrare astfel ]nc`t soluia s[ se apropie c`t mai mult de
soluia cerut[.

11.2. Aplicaţie – Goal Seek
O persoan[ depune o sum[ la o banc[, pe termen de o lun[, cu o rat[ a dob`nzii de
50%. S[ se calculeze, pentru un orizont de 12 luni suma din cont la ]nceputul =i sf`r=itul
fiec[rei luni. S[ se calculeze valoarea din cont la sf`r=itul perioadei pentru mai multe valori a
sumei depuse. S[ se determine ce sum[ trebuie s[ fie depus[ astfel ]nc`t la sf`r=itul perioadei
suma din cont s[ fie de 10000000 lei ?

Modelarea deciziilor utilizand foile de calcul

Se va crea urm[toarea foaie de calcul (figura 11.2):

Figura 11.2
Suma la ]nceputul lunii 1 este chiar suma depus[, deci ]n B5 vom introduce formula
ˆB1.
Suma la sf`r=itul unei luni este suma de la ]nceputul lunii la care se adaug[ dob`nda,
deci formula din celula C5 va fi ˆB5‡B5*B$2/12.
Suma la ]nceputul lunii 2 este suma de la sf`r=itul lunii 1, deci ]n B6 vom introduce
formula ˆC5.
Se copiaz[ pe coloan[ formulele din B6 =i B5. Suma de la sf`r=itul perioadei este ]n
celula C16. Valoarea din aceast[ celul[ depinde ]n mod indirect de suma depus[ din B1.
Dac[ se modific[ suma depus[, automat se modific[ =i valoarea din C16. De exemplu,
pentru o sum[ depus[ de 3000000 se va obine la sf`r=itul perioadei o sum[ de
4896282lei.
S[ rezolv[m acum urm[toarea ]ntrebare: Ce sum[ trebuie depus[ astfel ]nc`t la
sf`r=itul perioadei suma final[ s[ fie de 10000000 lei ?.
Rezolvare:
1. Se selecteaz[ celula C16.
2. Se aplic[ comanda Tools, Goal Seek
3. Caseta Goal Seek se va completa ]n modul urm[tor:
Set Cell
C16
Celula care conine suma pe care vrem sã o obinem
To Value
10000000
Suma pe care vrem sã o obinem (suma depusã)
By Changing Cell B1
Celula care variazã ca sã obinem rezultatul
4. Se selecteaz[ butonul OK
Excel rezolv[ problema ]n mod invers, suma care trebuie depus[ fiind de 6127097 lei.


11.3. Calcularea tabelelor de răspunsuri
Facilit[ile “What if“ - “Ce se ]nt`mpl[ dac[“ oferite de Excel sunt foarte folositoare
]n afaceri. Foile de calcul pot da r[spuns imediat la ]ntreb[ri cum ar fi: “Ce s-ar ]nt`mpla dac[
s-ar reduce costurile cu 0,5% ?”, “Ce s-ar ]nt`mpla dac[ s-ar vinde mai mult cu 10% ?”, “Ce
s-ar ]nt`mpla dac[ nu am primi ]mprumutul?”.
Atunci c`nd se testeaz[ c`t de mult afecteaz[ rezultatele o schimbare c`t de mic[ a
m[rimilor de intrare, se realizeaz[ o analiz[ de senzitivitate. Pentru a realiza o analiz[ de
senzitivitate pentru un domeniu mare de intr[ri se poate folosi comanda Table din meniul
Data. Comanda poate fi utilizat[ ]n dou[ moduri:
1. Modificarea unei date de intrare pentru a vedea efectul produs asupra uneia sau mai multor
formule.
2. Modificarea a dou[ date de intrare pentru a vedea efectul produs asupra unei formule.
Pentru a ]nelege mai bine ce face aceast[ comand[ s[ consider[m urm[torul exemplu:
S[ se calculeze ratele lunare care trebuie pl[tite pentru a returna un credit, cu o anumit[
dob`nd[.
Rezolvare:
1. Primul pas este crearea foii de calcul (figura 11.3).

Figura 11.3
}n celula B6 se introduce formula ˆ -PMT(B2/12,B3*12,B1), formul[ cu care se
calculeaz[ ratele lunare ce trebuie pl[tite pentru a returna creditul care se g[se=te ]n
B1, pe durata specificat[ ]n B3 (B3*12 reprezint[ num[rul de luni), cu dob`nda din
celula B2 (B2/12 reprezint[ dob`nda lunar[).
2. S[ facem o analiz[ de senzitivitate ]n care s[ analiz[m cum sunt influenate ratele lunare
de dob`nzi.
Se construie=te un tabel ]n care prima coloan[ sau prima linie conine valorile care trebuie
testate. Pentru exemplul nostru ]n domeniul A9:A13 conine ratele dob`nzii care vor fi
utilizate ca intr[ri ]n analiza de senzitivitate.
3. }n urm[toarele coloane (sau linii) din tabel, ]n celulele din capul de tabel se introduc
adresele formulelor care conin r[spunsul. }n cazul nostru ]n celula B8 se introduce
formula ˆB6 (B6 conine formula pentru calculul ratelor lunare).
4. Se selecteaz[ celulele care conin tabelul. Se aplic[ comanda Data, Table. Pe ecran apare
caseta de dialog Table (figura 11.3).

Figura 11.3 – caseta de dialog Table
5. Se introduce adresa celulei care conine variabila de intrare ]n Row Input Cell (dac[
valorile care sunt testate sunt desf[=urate pe linie ) sau Column Input Cell (dac[ valorile
care sunt testate sunt desf[=urate pe coloan[). }n cazul nostru, valorile testate sunt
desf[=urate pe coloan[ (A9/A13), deci vom introduce ]n Column Input Cell B2 (adresa
ratei dob`nzii).
Rezultatul obinut este un tabel care conine ratele lunare corespunz[toare fiec[rei dob`nzi.
}n continuare vom vedea cum poate fi folosit[ comanda Table pentru a vedea efectul
produs asupra unei formule prin modificarea a dou[ date de intrare.
Relu[m exemplul anterior numai c[ acum vom modifica dou[ date de intrare:
dob`nda =i creditul. }n foaia da calcul se va calcula rezultatul pentru mai multe combinaii ale
acestor valori.
Rezolvare:
1. Ca =i ]n cazul precedent se creeaz[ foaia de calcul (figura 11.4).
2. Se construie=te un tabel ]n care prima coloan[ =i prima linie conin valorile celor dou[
variabile. Colul din st`nga sus trebuie s[ conin[ o formul[ sau o referin[ la o formul[
}n exemplul nostru domeniul A9:A13 va conine valorile dob`nzilor, domeniul B8:F8
valorile creditului, iar celula A8 va conine formula ˆB6 (o referin[ la o celul[ care
conine formula de calcul).
3. Se selecteaz[ tabelul =i se aplic[ comanda Table. }n Row Input Cell se introduce adresa
celulei care reprezint[ variabila care are valorile desf[=urate pe linie, iar ]n Column
Input Cell se introduce adresa celulei care reprezint[ variabila care are desf[=urate
valorile pe coloan[. }n cazul nostru: ]n Row Input Cell se introduce B1; ]n Column
Input Cell se introduce B2.
Rezultatul este prezentat ]n tabelul din figura 11.4. Valorile din tabel reprezint[ ratele
lunare care trebuie pl[tite pentru diferite valori ale creditului =i diferite valori ale dob`nzii.

Figura 11.4


11.4. Efectuarea de analize “What if” cu scenarii
Multe din analizele economice implic[ efectuarea de analize de tipul “Ce se ]nt`mpl[
dac[?”. Pentru a r[spunde la astfel de ]ntreb[ri se modific[ valorile din celulele care conin
datele iniiale ale problemei. La schimbarea acestor valori se modific[ =i rezultatele. Cu c`t
exist[ mai multe scenarii, cu at`t urm[rirea diferenelor dintre rezultatele acestora este mai
dificil[. Excel ofer[ o facilitate care permite urm[rirea acestor scenarii: “Scenario Manager”
(managerul de scenarii).

11.5. Crearea unui scenariu
Un model cu scenarii trebuie s[ aib[ un set de valori de intrare =i un set de valori
rezultat (care se schimb[ ]n funcie de intr[ri).
Pentru a crea un scenariu se vor efectua urm[torii pa=i:
1. Se aplic[ comanda Tools, Scenarios. Pe ecran apare caseta de dialog Scenario Manager
(figura 11.5).

Figura 11.5 - caseta de dialog Scenario Manager
2. Din caseta Scenario Manager se selecteaz[ butonul Add. Pe ecran apare caseta de dialog
Add Scenario (figura 11.6).


Figura 11.6 – caseta de dialog Add Scenario
3. }n caseta Scenario Name se specific[ numele scenariului.
}n caseta Changing Cells se indic[ celulele sau domeniul de celule care vor fi modificate
pentru fiecare scenariu.
}n caseta Comment se pot scrie informaii suplimentare. Automat Excel introduce ]n
aceast[ caset[ numele utilizatorului =i data la care a fost creat scenariul.
Pentru a evita efectuarea de modific[ri ]n celulele din foaia de calcul se selecteaz[
optiunea Prevent Changes din seciunea Protection a casetei de dialog. Pentru a ascunde
datele din celule se selecteaz[ opiunea Hide.
4. Se aplic[ un clic pe butonul OK.
Pe ecran apare caseta de dialog Scenario Values (figura 11.7), ]n care se introduc datele
pentru fiecare celul[ din scenariu.

Figura 11. 7 – caseta de dialog Scenario Values
Dup[ introducerea datelor se selecteaz[ butonul OK. Pe ecran apare caseta de dialog
Scenario Manager. Denumirea noului scenariu creat apare ]n lista Scenarios. La
selectarea unui scenariu din list[ ]n c`mpul Changing Cells vor fi afi=ate adresele
celulelor din scenariu, iar ]n c`mpul Comments comentariile introduse.
5. Pentru a vedea scenariul se selecteaz[ denumirea lui din list[ =i se execut[ un clic pe
butonul Show. Excel va afi=a valorile din toate celulele din foaia de calcul. }n cazul ]n
care caseta de dialog acoper[ o parte din date, se trage cu mouse-ul bara de titlu a casetei
de dialog spre marginea ecranului.
6. Pentru a reveni ]n foaia de calcul se execut[ un clic pe butonul Close. Excel va afi=a ]n
foaia de calcul valorile stabilite ]n scenariu.

Este bine ca atunci c`nd se lucreaz[ cu scenarii fiecare celul[ din scenariu s[ aib[ un
nume. Excel va folosi aceste nume ]n caseta de dialog Scenario Values =i ]n rapoartele
pentru scenarii.

Figura 11. 8 – caseta de dialog Define Name
Pentru a atribui un nume unei celule se efectueaz[ urm[torii pa=i:
1. Se selecteaz[ celula c[reia trebuie s[ i se atribuie un nume.
2. Se aplic[ comanda Insert, Name, Define. Pe ecran apare caseta de dialog Define Name
(figura 11.8).
3. Se scrie numele celulei ]n caseta Names.

11.6. Editarea şi ştergerea scenariilor
Un scenariu existent poate fi modificat sau poate fi =ters.
Pentru a =terge un scenariu se selecteaz[ numele acestuia din caseta de dialog
Scenario Manager =i se aplic[ un clic pe butonul Delete. Excel va elimina scenariul din lista
cu scenarii.

Figura 11. 9 – caseta de dialog Edit Scenario
Pentru a modifica un scenariu se selecteaz[ numele scenariului din caseta de dialog
Scenario Manager =i se aplic[ un clic pe butonul Edit Scenario. Pe ecran apare caseta de
dialog Edit Scenario (figura 11.9), asem[n[toare cu caseta Add Scenario. Se efectueaz[

toate modific[rile necesare =i se aplic[ un clic pe butonul OK. Pe ecran apare caseta de
dialog Scenario Values ]n care se introduc noile valori.

11.7. Sintetizarea scenariilor prin rapoarte
Pentru compararea rezultatelor din mai multe scenarii, Excel ofer[ dou[ metode. La
prima metod[ se creeaz[ un raport simplu sub form[ de tabel, ]n care sunt prezentate datele
din celulele de intrare =i efectul lor asupra rezultatelor. La a doua metod[ se genereaz[ un
tabel pivot.

11.8. Crearea unui raport de sintetizare
Pentru a crea un raport de sintetizare se efectueaz[ urm[torii pa=i:
1. Se aplic[ comanda Tools, Scenarios.
2. Se aplic[ un clic pe butonul Summary. Pe ecran apare caseta de dialog Scenario
Summary (figura 11.10)

Figura 11. 10 – caseta de dialog Scenario Summary
3. Din zona Report Type se selecteaz[ opiunea Scenario Summary.
}n caseta Result Cells se indic[ domeniul de celule rezultat (care conin formulele bazate
pe celule cu datele iniiale).
Excel va afi=a o nou[ foaie de calcul cu un tabel ce conine pentru datele iniiale =i
rezultatele din fiecare scenariuscenariu.

11.9. Crearea unui raport de tip tabel pivot pentru scenarii
Tabelele pivot sunt tabele obinute prin gruparea ]n diverse moduri a informaiilor din
r`ndurile =i coloanele unui tabel. Pentru a crea un tabel pivot plec`nd de la scenariile din
foaia de calcul se vor efectua urm[torii pa=i:
2. Se aplic[ un clic pe butonul Summary.
3. Din caseta de dialog Scenario Summary se selecteaz[ opiunea Scenario Pivot
Table. }n caseta text Result Cells se indic[ domeniul de celule care conine
formulele bazate pe celulele cu datele iniiale.
Excel va afi=a o nou[ foaie de calcul cu un tabel pivot ce conine datele de pornire =i
rezultatele scenariului.


11.10. Aplicaţie - Elaborarea de alternative de buget
Pentru a echilibra un buget trebuie g[sit[ cea mai bun[ modalitate de a repartiza
departamentelor resursele disponibile. Atunci c[nd prevederile iniiale sunt dep[=ite trebuie
comparate strategiile de redistribuire. Cu facilit[ile oferite de managerul de scenarii se pot
modela diferite strategii pentru a analiza avantajele =i dezavantajele diferitelor moduri de
abordare.

Figura 11.11
}n coloana Buget proiectat sunt introduse prevederile iniiale ale bugetului.
}n coloana Buget repartizat sunt introduse bugetele repartizate fiec[rui departament.
}n coloana Diferen[ se va calcula diferena dintre bugetul repartizat =i bugetul
proiectat. }n celula D2 se va introduce formula ˆB2-C2, care se va copia ]n domeniul D3:D5.
}n coloana Procent se va calcula procentul cu care se dep[=e=te bugetul proiectat. }n
celula E2 se va introduce formula ˆD2/C2. Aceast[ formul[ se va copia ]n domeniul E3:E5.
}n ultima linie din tabel se vor calcula totalurile: bugetul total repartizat, bugetul total
proiectat, diferena total[ =i procentul de dep[=ire total. Celulele din aceast[ linie vor conine
urm[toarele formule:
B6: =Sum(B2:B5)
C6: =Sum(C2:C5)
D6: =B6-C6
E6: =D6/C6
Folosind facilitatea Goal Seek s-ar putea r[spunde la ]ntreb[ri de tipul: “C`t de mult
ar putea s[ scad[ bugetul repartizat pentru departamentul Desfacere astfel ]nc`t s[ se reduc[
dep[=irea bugetului total?”.
Dep[=irea bugetului total se g[se=te ]n celula E6. Aici ar trebui s[ obinem valoarea 0.
Bugetul pentru departamentul Desfacere se g[se=te ]n celula B5.
Pentru rezolvarea problemei:
1. Se aplic[ comanda Tools, Goal Seek.
2. Caseta de dialog Goal Seek se completeaz[ ]n modul urm[tor: Set Cell - E6, To Value 0, By Changing Cell - B5.
Dup[ aplicarea comenzii celula B5 va conine bugetul care trebuie repartizat
departamentului Desfacere astfel ]nc`t bugetul total s[ nu fie dep[=it.
Pentru a testa mai multe strategii de repartizare a bugetului se poate folosi managerul
de Scenarii.
Rezolvare:
Se denumesc celulele B2:B5:
1. Se selecteaz[ celula B2.

2. Se aplic[ comanda Insert, Name, Define.
3. }n caseta Name din caseta de dialog Define Name se introduce Buget Marketing.
4. Se aplic[ un clic pe butonul OK
Folosind aceea=i metod[ se vor denumi =i celulele B3:B5, B6:E6 ]n modul urm[tor:
B3 - Buget Aprovizionare,
B4 - Buget Resurse Umane,
B5 - Buget Desfacere.
B6 – Total buget repartizat
C6 – Total buget proiectat
D6 – Diferena total[
E6 – Procent de dep[=ire total
Se vor crea mai multe scenarii care vor conine diferite valori pentru bugetele repartizate
pentru cele patru departamente:
2. Din caseta de dialog Scenario Manager se selecateaz[ butonul Add.
3. }n caseta Scenario Name se introduce numele scenariului: Estim[ri iniiale. }n caseta
Changing Cells se indic[ celulele care vor fi modificate: B2:B5. Se aplic[ un clic pe
butonul OK.
4. }n caseta de dialog Scenario Values se vor introduce datele specifice pentru fiecare
scenariu.
B2: 956750000
B3: 244120000
B4: 370000000
B5: 145188000
Folosind pa=ii 2-4 se vor mai crea urm[toarele scenarii:
Valori specifice scenariilor
B2
B3
B4
Scenariu1
956750000
244120000
370000000
Scenariu2
956750000
23970000
320000000

B5
1252130000
1000000000

Dup[ crearea scenariilor, pentru compararea acestora se poate crea un raport.
1. }n caseta de dialog Scenario Manager se aplic[ un clic pe butonul Summary.
2. }n caseta de dialog Scenario Summary, se selecteaz[ opiunea Scenario Summary, iar
]n Result Cells se introduce domeniul B6:E6 (domeniul care conine rezultatele).
Excel creeaz[ o nou[ foaie de calcul cu un tabel ]n care sunt afi=ate pentru fiecare
scenariu valorile de intrare =i valorile rezultat.

Utilizarea Solver-ului

CAPITOLUL 12
UTILIZAREA SOLVER-ULUI
12.1. Solver - ul
Cu comanda Goal Seek se poate analiza variaia rezultatelor ]n funcie de o singur[
celul[ de pornire. Multe foi de calcul sunt prea complexe pentru comanda Goal Seek. La
unele modele pot fi necesare intr[ri multiple sau se pot impune restricii asupra unora dintre
valorile de intrare sau asupra rezultatului. Analiza unui rezultat prin modificarea valorilor din
una sau mai multe celule se poate face utiliz`nd facilitatea Solver din Excel.
Pentru a putea fi folosit[ facilitatea Solver, ea trebuie mai ]nt`i instalat[. Pentru a
realiza acest lucru se vor executa urm[torii pa=i:
1. Se aplic[ comanda Tools, Add-Ins. Pe ecran apare caseta Add-Ins (figura 12.1).

Figura 12.1 – caseta de dialog Add - Ins
2. Se marcheaz[ opiunea Solver.
3. Se selectez[ butonul OK. Comanda Solver va aparea ]n meniul Tools.
Cu Solver-ul se pot rezolva tot felul de probleme de programare liniar[ =i neliniar[:
• Probleme de maximizare a c`=tigurilor
• Probleme de transport
• Probleme de amestec
• Probleme de minimizare a costurilor
Aceste tipuri de probleme vor fi tratate ]n detaliu ]n partea a doua – Modelarea
deciziilor utiliz`nd foile de calcul.
}n principiu problemele care pot fi rezolvate au un singur obiectiv, pentru unele
variabile sunt specificate restricii, iar variabilele de intrare influeneaz[, direct sau indirect,
at`t restriciile c`t =i valorile care trebuie optimizate.
Pentru utilizarea Solver-ului se vor efectua urm[torii pa=i:

1. Se configureaz[ foaia de calcul =i se stabile=te care sunt celulele care conin variabilele de
intrare =i rezultatul.
2. Se aplic[ comanda Tools, Solvers. Pe ecran apare caseta de dialog Solver Parameters
(figura 12.2).

Figura 12.2 – caseta de dialog Solver Parameters
}n caseta text Set Target Cell se specific[ celula care conine formula cu rezultatul care
trebuie analizat (funcia obiectiv). }n seciunea Equal To se specific[ ce se urm[re=te
pentru funcia obiectiv:
• Dac[ trebuie maximizat[ se selecteaz[ opiunea Max.
• Dac[ trebuie minimizat[ se selecteaz[ optiunea Min.
• Dac[ funcia obiectiv trebuie s[ ating[ o anumit[ valoare se selecteaz[ opiunea
Value of, iar ]n caseta text al[turat[ se introduce valoarea respectiv[.
}n caseta text By Changing Cells se vor indica celulele sau domeniul de celule pe care
Solver-ul le va modifica pentru a obine valoarea optim[.
Caseta Subject to the Constraints va conine restriciile problemei. Pentru a ad[uga o
restricie se aplic[ un clic pe butonul Add. Pe ecran apare o nou[ caset[ de dialog, Add
Constraint (figura 12.3) ]n care se pot introduce restriciile problemei:

Figura 12.3 – caseta de dialog Add Constraint
Pentru a stabili o restricie:
• }n caseta text Cell Reference se va specifica celula care conine formula pe care se
bazeaz[ restricia.

Se aplic[ un clic pe s[geata de derulare pentru a vedea lista cu operatori pentru
restricii =i se selecteaz[ operatorul corespunz[tor.
• }n ultima caset[ text se scrie valoarea restriciei ce trebuie respectat[.
• Se aplic[ un clic pe butonul Add pentru a introduce =i alte restricii.
• Pentru a reveni ]n caseta de dialog Solver Parameters se aplic[ un clic pe butonul
OK. Restriciile definite vor fi afi=ate ]n caseta Subject to the Constraints.
4. Se aplic[ un clic pe butonul Solver. Solver-ul va ]ncepe efectuarea calculelor pentru
soluiile optime. Dup[ ce g[se=te o soluie, pe ecran apare caset[ de dialog Solver
Results (figura 12.4).
•

Figura 12.4 – caseta de dialog Solver Results
Excel introduce soluiile ]n foaia de calcul. Dac[ se alege opiunea Keep Solver
Results Excel va p[stra ]n foaia de calcul soluia calculat[.
Dac[ se selecteaz[ opiunea Restore Original Values, se va reveni la valorile iniiale
din foaia de calcul. Pentru sintetizarea rezultatelor g[site, Solver-ul permite generarea a trei
tipuri de rapoarte:
• Answer - ]n care sunt prezentate valorile iniiale =i finale pentru celula rezultat =i
celulele care conin variabilele de intrare.
• Sensitivity - ]n care este prezentat[ o analiz[ de senzitivitate a variabilelor de intrare
(cum variaz[ rezultatul la diferite modific[ri ale variabilelor de intrare).
• Limits - se specific[ ]ntre ce limite pot varia limitelele impuse ]n restricii, astfel ]ncât
rezultatul final s[ nu se modifice.
Mai multe detalii despre aceste rapoarte sunt prezentate ]n partea a-II-a – Modelarea
deciziilor utiliz`nd foile de calcul.
Pentru a crea un raport se selecteaz[ denumirea lui din lista Reports din caseta Solver
Results. Pentru a selecta mai multe rapoarte din list[, se alege primul raport, se ine ap[sat[
tasta <Ctrl> =i se aplic[ un clic pe unul sau ambele rapoarte r[mase. Se aplic[ un clic pe
butonul OK. Excel va crea fiecare raport ]ntr-o foaie de calcul separat[.

12.2. Modificarea configuraţiei Solver-ului
Utilizatorul poate specifica tehnica utilizat[ de programul Solver pentru g[sirea
r[spunsurilor, precizia r[spunsurilor =i perioada de lucru a programului Solver.
Pentru a realiza acest lucru din caseta de dialog Solver Parameters se selecteaz[
butonul Options. Pe ecran apare caseta de dialog Solver Options (figura 12.5). Folosind
opiunile din aceast[ caset[ de dialog se poate stabili modulul ]n care va lucra Solver-ul.
}n caseta Max Time se specific[ timpul maxim (]n secunde) pe care programul
Solver poate s[ ]l foloseasc[ pentru g[sirea unei soluii.

}n caseta Iterations se specific[ num[rul maxim de iteraii pe care le poate face
Solver-ul.
}n caseta Precision se specific[ c`t de apropiate trebuie s[ fie dou[ ]ncerc[ri de
soluie, ]nainte de a declara g[sit[ cea mai bun[ soluie.
}n caseta Tolerance se specific[ (]n procente) c`t de aproape de cea mai bun[ soluie
trebuie s[ fie r[spunsul, atunci c`nd se lucreaz[ cu probleme cu numere ]ntregi. Stabilirea
unei tolerane mai mari poate m[ri considerabil viteza de calcul atunci c`nd se lucreaz[ cu
probleme complexe cu numere ]ntregi
Opiunea Assume Linear Model configureaz[ Solver-ul s[ utilizeze o metod[ de
programare liniar[ pentru g[sirea soluiei. Dac[ foaia de calcul conine o problem[ neliniar[,
apare un mesaj de avertisment.
Opiunea Show Iterations Results permite afi=area soluiilor intermediare.
Continuarea se face ap[s`nd pe butonul Continue, oprirea pe butonul Stop.
Opiunile Tangent sau Quadratic sunt metode adiionale folosite pentru g[sirea
soluiei. Se recomand[ utilizarea opiunii Quadratic dac[ foaia de calcul conine formule
complexe care sunt neliniare.
Opiunile din seciunea Derivatives permit specificarea metodei de derivare parial[
folosite.
Opiunile din seciunea Search permit specificarea metodei de c[utare folosit[.

Figura 12.5 – caseta de dialog Solver Options

12.3. Aplicaţie
O companie are trei fabrici ]n localit[ile A, B, C. Produsele realizate ]n aceste fabrici
sunt distribuite din localit[ile S =i P. Compania analizeaz[ posibilitatea de amplasare a unui
nou depozit ]n localitatea R. Analizele efectuate au stabilit urm[toarele costuri de transport:
Costul Transportului ]n depozitele din:
Fabrici
S
P
R
A
10
14
8
B
12
10
12
C
8
12
10
Capacit[ile de producie la fabricile din localit[ile A, B, C sunt de 20, 30 =i 40
unit[i pe s[pt[m`n[.
Se estimeaz[ c[ depozitul din R va absolvi 20 de unit[i pe s[pt[m`n[, iar cele din S
=i P, 40 respectiv 30 de unit[i pe s[pt[m`n[.

S[ se determine modul de distribuie a produselor la depozite astfel ]nc`t costurile de
transport s[ fie minime.
Modelul va avea 9 variabile:
x1 - num[rul de produse transportate de la fabrica A la depozitul S
x2 - num[rul de produse transportate de la fabrica A la depozitul P
x3 - num[rul de produse transportate de la fabrica A la depozitul R
x4 - num[rul de produse transportate de la fabrica B la depozitul S
x5 - num[rul de produse transportate de la fabrica B la depozitul P
x6 - num[rul de produse transportate de la fabrica B la depozitul R
x7 - num[rul de produse transportate de la fabrica C la depozitul S
x8 - num[rul de produse transportate de la fabrica C la depozitul P
x9 - num[rul de produse transportate de la fabrica C la depozitul R
Restriciile modelului sunt:
1. x1‡x2‡x3<=20 (Producia din fabrica A sa nu dep[=easc[ capacitatea de productie)
2. x4‡x5‡x6<=30 (Producia din fabrica B sa nu dep[=easc[ capacitatea de productie)
3. x7‡x8‡x9<=40 (Producia din fabrica C sa nu dep[=easc[ capacitatea de productie) C)
4. x1‡x4‡x7>=20 (numarul de produse transportate în depozitul A sã fie mai mare decât
cererea la depozitul respectiv)
5. x2‡x5‡x8 >=40 (numarul de produse transportate în depozitul B sã fie mai mare decât
cererea la depozitul respectiv )
6. x5‡x6‡x9 >=30 (numarul de produse transportate în depozitul C sã fie mai mare decât
cererea la depozitul respectiv )
Functia obiectiv a modelului este minimizarea cheltuielilor de transport. Cheltuielile de
transport sunt egale cu
10x1‡14x2‡8x3‡12x4‡10x5‡12x6‡8x7‡12x8‡10x9
Pentru rezolvarea acestei probleme se va configura foaia de calcul în modul urmãtor (figura
12.6):

Figura 12.6

Celulele din meniul C3:E5 vor conine variabilele modelului. La ]nceput aceste celule
se vor completa cu date aleatoare, s[ presupunem c[ toate variabilele sunt egale cu 1. }n urma
rezolv[rii problemei ]n aceste celule se va obine rezultatul.
}n celulele B3, B4, B5 se va calcula producia total[ realizat[ ]n fiecare fabric[.
}n B3 se va introduce formula =SUM(C3:E3) =i se copiaz[ formula ]n B4 =i B5.
}n celulele C6, D6, E6, se va calcula producia depozitat[ ]n fiecare depozit. }n celula
C6 se va introduce formula =SUM(C3:C5). Aceast[ formul[ se copiaz[ ]n D6 =i E6.
Celulele B10, B11, B12 vor conine capacit[ile de producie la fabricile A, B, C.
Celulele C13, D13, E13 vor conine cererea la cele 3 depozite.
}n domeniul C10:E12 se vor introduce cheltuielile de transport pe unitatea de produs
de la fiecare fabric[ la fiecare depozit.
}n celulele C15, D15, E15 se calculeaz[ cheltuielile de transport la fiecare depozit. }n
celula C15 se introduce formula=C3*C10+C4*C11+C5*C12 (Num[rul de produse
transportate de la fabrica A la depozitul S * cheltuielile de transport + num[rul de produse
transportate de la fabrica B la depozitul S * cu cheltuielile de transport + num[rul de produse
transportate de la fabrica C la depozitul S * cheltuielile de transport.). Aceast[ formul[ se
copiaz[ ]n celulele d15 =i E15.
}n celula B15 se vor calcula cheltuielile cu transportul. }n aceast[ celul[ se va
introduce formula = SUM( C15:E15).
Restriciile problemei pentru foaia de calcul proiectat[ vor fi:
1.
B3<=B10 Producia din fabrica A s[ nu dep[=easc[ capacitatea de producie.
2.
B4<=B11 Producia din fabrica B s[ nu dep[=easc[ capacitatea de producie
3.
B5<=B12 Producia din fabrica s[ nu dep[=easc[ capacitatea de producie
4.
C6>=C13 s[ nu existe rupere de stoc la depozitul S
5.
D6>=D13 s[ nu existe rupere de stoc la depozitul P
6.
E6>=E13 s[ nu existe rupere de stoc la depozitul R
7.
C3:E5>=0 Toate variabilele s[ fie numere negative
Dup[ ce foaia de calcul a fost configurat[, din meniul Tools se aplic[ comanda Solver.
Obiectivul problemei este minimizarea cheltuielilor totale de transport. Aceast[
valoare este calculat[ ]n celula B15, deci ]n Set Target Cell se introduce B15. Funcia trebuie
minimizat[, deci se va alege opiunea Min.
Celulele care conin variabilele de intrare sunt ]n domeniu C3:E5, deci ]n By
Changing Cells se introduce C3:E5.
}n caseta Subject to the Constrains sevor introduce restriciile problemei:
• Se selecteaz[ butonul Add.
• }n caseta Cell Reference se introduce B3.
• Din lista cu operatori se selecteaz[ <=.
• }n caseta Constraint se introduce B10.
• }n mod similar se introduc =i celelalte restrricii.
}n final caseta Solver va fi completat[ ca ]n figura 12.7


Figura 12.7
Se selecteaz[ butonul Options. }n caseta de dialog Solver Options se marcheaz[
opiunile Assume Linear Model =i Assume Non Negative. Se selecteaz[ butonul OK.
}n acest moment se poate selecta ]n caseta de dialog Solver Parameters butonul
Solve.
}n caseta Solver Results se selecteaz[ opiunea Keep Solver Solutions =i cele trei
rapoarte. Se selecteaz[ butonul OK.
Solver-ul rezolv[ problema. Rezultatul obinut este:se vor transporta 20 de produse de
la fabrica A la depozitul R, 30 de produse de la fabrica B la depozitul P, 20 de produse de la
fabrica C la depozitul S, 10 de produse de la fabrica C la depozitul P 10 de produse de la
fabrica C la depozitul R.

Rezolvarea problemelor de programare liniară

CAPITOLUL 13
REZOLVAREA PROBLEMELOR DE PROGRAMARE LINIARÃ
13.1. Rezolvarea problemelor şi procesul de luare a deciziilor
}n general, prin <problem[> se ]nelege o dificultate care nu poate fi dep[=it[ ]n mod
automat. Procesul de rezolvare a unei probleme poate fi definit ca procesul de identificare a
diferenelor dintre starea actual[ =i starea dorit[ a unei afaceri =i stabilirea aciunilor necesare
pentru a rezolva aceast[ diferen[. Pentru probleme destul de complicate care s[ justifice
timpul =i efortul unei analize am[nunite, procesul de rezolvare a unei probleme implic[
parcurgerea urm[torilor pa=i:
1. Identificarea =i definirea problemei.
2. Determinarea unui set de soluii alternative.
3. Determinarea unui criteriu sau a unor criterii pentru evaluarea alternativelor.
4. Evaluarea alternativelor.
5. Alegerea unei alternative.
6. Implementarea alternativei alese.
7. Evaluarea rezultatelor =i verificarea dac[ a fost selectat[ o soluie satisf[c[toare.
Luarea deciziilor este un termen ]n general asociat cu primele cinci etape ale procesului
de rezolvare a unei probleme. Astfel, prima etap[ ]n luarea unei decizii este identificarea =i
definirea problemei, iar ultima etap[ este alegerea unei alternative, care de fapt este actul de
luare a deciziei (figura 13.1).
S[ consider[m urm[toarea situaie. Un absolvent de facultate ]=i caut[ un serviciu. Ca
urmare a cererilor depuse, absolventul prime=te mai multe oferte situate ]n localit[i diferite:
Bucure=ti, Timi=oara, Constana, Bra=ov. Alternativele pentru acest caz de luare a deciziei
sunt:
1. Acceptarea postului din Bucure=ti.
2. Acceptarea postului din Timi=oara.
3. Acceptarea postului din Constana.
4. Acceptarea postului din Bra=ov.
Urm[torul pas al procesului de luare a deciziei este stabilirea criteriilor ce vor fi folosite
]n evaluarea alternativelor. Problemele decizionale ]n care obiectivul este de a g[si cea mai
bun[ soluie ]n raport cu un singur criteriu se numesc decizii cu un singur obiectiv. Desigur,
un criteriu important este salariul, dar pot exista =i alte criterii: posibilitatea de avansare,
localitatea, posibilitatea de a avea o locuin[. Problemele decizionale ]n care decizia este
luat[ ]n funcie de mai multe criterii se numesc decizii multicriteriale.
Urm[torul pas este evaluarea fiec[rei altenative ]n raport cu fiecare criteriu. Unele
criterii sunt u=or de evaluat (cum ar fi salariul), altele pot fi evaluate pe baza unor factori
subiectivi (potenialul de avansare, localitatea). }n general, la factorii subiectivi, pentru
fiecare variant[ se acord[ un calificativ sau o not[. De foarte multe ori criteriile sunt
contradictorii. O alternativ[ bun[ prin aplicarea unui criteriu poate s[ nu fie la fel de bun[
prin aplicarea celorlalte criterii.
Pentru evaluarea primului tip de criterii se folosesc metodele cantitative, pentru cel de al
doilea tip, metodele calitative.
}n abordarea cantitativ[ analistul se va concentra asupra datelor asociate problemei =i va
dezvolta un model matematic care va descrie obiectivele, restriciile sau alte relaii care
exist[ ]n problem[. Ulterior, prin utilizarea metodelor cantitative, analistul va face o alegere
]n funcie de datele problemei.

Analiza calitativ[ se bazeaz[ mai mult pe intuiie =i experien[. Dac[ managerul a avut
experiene similare, problema este relativ simpl[. Dac[ managerul nu are experien[ ]n
probleme similare sau problema este prea complex[, pentru luarea deciziei finale se
recomand[ metodele cantitative.
Definirea
problemei

Identificarea
alternativelor

Determinarea
criteriilor

Analiza
cantitativ[

Analiza
calitativ[

Evaluarea
alternativelor
Luarea deciziei

Figura 13.1 – Procesul de luare a deciziei

13.2. Dezvoltarea modelelor
Modelele sunt reprezent[ri ale unor obiecte sau situaii reale. Ele pot exista ]n mai
multe forme. De exemplu, o machet[ a unui avion este o reprezentare a unui avion adev[rat.
Similar, un camion de juc[rie este modelul unui camion adev[rat. Aceste dou[ exemple de
modele sunt replici fizice ale obiectelor reale. Folosind terminologia adecvat[, ele sunt
modele fizice sau modele iconice.
O alt[ categorie de modele include obiectele care exist[ ]n form[ fizic[, dar nu au
acela=i aspect ca =i obiectul modelat. Acestea sunt modelele analogice. Cutia de viteze a unui
automobil este un model analogic: poziia acului indic[ viteza automobilului. Un termometru
este un alt model analogic pentru reprezentarea temperaturii.
A treia categorie include acele modele care reprezint[ o problem[ sub forma unui set de
relaii matematice. Aceste modele se numesc modele matematice. De exemplu, profitul total
obinut prin v`nzarea unui produs poate fi calculat ]nmulind profitul unitar cu cantitatea
v`ndut[. Dac[ x reprezint[ num[rul de unit[i v`ndute, P profitul total, atunci pentru un profit

unitar de 1000 lei, modelul matematic care stabile=te profitul total ]n funcie de v`nz[ri este
Pˆ1000*x.
Scopul utiliz[rii modelelor este realizarea unei interfee cu situaia real[ prin studierea
=i analizarea modelului. De exemplu, un constructor de avioane poate testa un model fizic
pentru a verifica caracteristicile de zbor ale unui avion adev[rat. Similar, un model
matematic poate fi utilizat pentru a analiza ce profit va fi obinut dac[ un produs este v`ndut.
Pentru cazul prezentat, dac[ vor fi v`ndute 30 de buc[i (xˆ30), profitul obinut va fi de
30*1000ˆ30000 lei.
Utilizarea modelelor matematice reduce cheltuielile =i timpul necesar pentru rezolvarea
unei probleme reale. O machet[ de avion se construie=te mai repede =i este mai ieftin[ dec`t
un avion real. La fel, prin utilizarea modelului matematic, se poate calcula rapid profitul ce
poate fi obinut, f[r[ ca managerul s[ produc[ =i s[ v`nd[ cele x unit[i.
Modelele au =i avantajul reducerii riscului asociat, prin experimentarea unei situaii
reale. Pentru exemplele prezentate se pot evita gre=elile de proiectare, care ar putea duce la
pr[bu=irea avionului, sau se pot evita deciziile gre=ite care ar duce la pierderi de milioane de
lei.
Concluziile obinute depind de c`t de bine reprezint[ modelul situaia real[. Cu c`t
modelul se apropie mai mult de cazul real, cu at`t rezultatele vor fi mai precise.
}n continuare vor fi analizate numai modelele matematice. Principalele aspecte abordate
se refer[ la utilizarea metodelor cantitative ]n procesul de luare a deciziei. Accentul este pus
nu pe metodele propriu-zise, ci pe modul ]n care ele pot fi rezolvate utiliz`nd foile de calcul.

13.3. Modele matematice
}n majoritatea cazurilor ]n care se ]ncearc[ rezolvarea unor probleme manageriale se
constat[ c[ modul ]n care este structurat[ problema conduce la obinerea unui obiectiv
specific (cum ar fi maximizarea unui profit sau minimizarea unui cost). De asemenea, se
constat[ c[ de multe ori exist[ o serie de restricii sau constr`ngeri (cum ar fi capacitatea de
producie). Succesul folosirii analizei cantitative depinde de acurateea cu care obiectivul =i
restriciile sunt exprimate sub form[ de ecuaii =i relaii matematice.
Expresia matematic[ care descrie obiectivul problemei se nume=te funcie obiectiv. De
exemplu, ecuaia Pˆ10*x poate fi funcia obiectiv a unei firme care ]ncearc[ s[ maximizeze
profitul.
Relaiile matematice care descriu constr`ngerile problemei se numesc restricii. Dac[
de exemplu pentru a produce o unitate de produs sunt necesare 5 ore =i ]ntr-o s[pt[m`n[ se
lucreaz[ doar 40 de ore, atunci relaia 50*xˆ40 este o restricie de timp. 5*x reprezint[
timpul total necesar pentru a produce x unit[i, care trebuie s[ fie mai mic sau egal cu cele 40
de ore disponibile.
Problema de decizie este urm[toarea: C`te unit[i trebuie produse ]ntr-o s[pt[m`n[
pentru a maximiza profitul? Modelul matematic al acestei probleme este:
Max P = 10 * x

functia obiectiv

5 * x ≤ 40
 restrictii
x≥0 
Restricia xŽˆ0 este necesar[ deoarece nu se poate fabrica un num[r negativ de
produse.


13.4. Metoda programării liniare
Programarea liniar[ este o metod[ de rezolvare a problemelor de luare a deciziei.
Urm[toarele tipuri de aplicaii sunt specifice pentru rezolvarea lor cu ajutorul program[rii
liniare:
1. Un manager trebuie s[ stabileasc[ pentru perioada urm[toare programul de
producie =i nivelul stocurilor astfel ]nc`t s[ fie satisf[cut[ cererea de pe pia[ =i ]n
acela=i timp vrea s[ minimizeze costul total de producie =i costurile de stocare.
2. Un analist financiar trebuie s[ selecteze pentru un portofoliu de investiii cea mai
bun[ combinaie de aciuni =i obligaiuni. Aceste investiii trebuie selectate astfel
]nc`t s[ se maximizeze eficiena investiiei.
3. Un director de marketing trebuie s[ stabileasc[ modul ]n care va distribui bugetul
pentru publicitate ]n diverse medii: radio, televiziune, ziare =i reviste, astfel ]nc`t
efectul reclamei f[cute s[ fie maxim.
4. O companie are depozite ]n c`teva ora=e din ar[ =i prime=te comenzi de la clieni
din diverse localit[i. Se pune problema determin[rii cantit[ilor care vor fi trimise
de la depozite spre clieni astfel ]nc`t costurile totale de transport s[ fie
minimizate.
Acestea sunt doar c`teva exemple ]n care programarea liniar[ a fost utilizat[ cu succes,
dar lista poate continua. Ce au ]n comun aceste exemple este faptul c[ ele ]ncearc[ s[
minimizeze sau s[ maximizeze ceva. }n primul exemplu managerul vrea s[ minimizeze
costurile; ]n exemplul 2 analistul financiar vrea s[ maximizeze eficiena investiiei; ]n
exemplul 3 directorul de marketing trebuie s[ maximizeze eficiena reclamei; ]n exemplul 4
trebuie minimizate cheltuielile de transport. }n toate problemele de programare liniar[,
obiectivul este maximizarea sau minimizarea unor cantit[i.
Toate problemele de programare liniar[ au =i o a doua proprietate: restriciile care
limiteaz[ gradul ]n care obiectivul poate fi realizat. }n exemplul 1 producia este limitat[ de
capacitatea de producie =i ]n acela=i timp trebuie s[ satisfac[ cererea; ]n exemplul 2 analistul
este limitat de suma disponibil[ =i tipul aciunilor existente; ]n exemplul 3 directorul de
marketing este constr`ns de bugetul fixat =i de disponibilitatea mediilor de reclama; ]n
exemplul 4 cantit[ile ce pot fi transportate sunt limitate la disponibilul din fiecare depozit.
Deci, restriciile sunt o alt[ tr[s[tur[ general[ a fiec[rei probleme de programare liniar[.
Exemplu
Firma ABC produce o varietate de produse chimice. }n cadrul unui proces de producie,
pentru a produce dou[ produse (un aditiv =i un solvent) sunt necesare trei tipuri de materii
prime. Aditivul este v`ndut fabricilor de ulei =i este folosit la producerea a diverse tipuri de
combustibil. Solventul este v`ndut combinatelor chimice =i este utilizat la fabricarea
detergenilor. Pentru a fabrica aditivul =i solventul cele trei materii prime sunt amestecate ]n
proporiile indicate ]n tabelul 13.1.
Produs
Material 1
Material 2
Material 3

Aditiv
2
/5
0
3
/5

Solvent
½
1
/5
3
/10

Tabelul 13.1 – Necesarul de materii prime pentru obinerea unei tone de adidiv/solvent


Pentru a obine o ton[ de aditiv se amestec[ 2/5 tone de material 1=i 3/5 tone de material
3. O ton[ de solvent poate fi obinut[ prin amestecarea a ½ tone de material 1, 1/5 tone de
material 2 =i 3/10 tone de material 3.
Producia este limitat[ de disponibilitatea celor trei materii prime. }n prezent firma
dispune de 20 tone de material 1, 5 tone de material 2 =i 21 tone de material 3. Prin natura
procesului de producie, materiile prime care nu sunt utilizate ]n procesul de producie curent
sunt considerate de=euri.
Fiecare ton[ de aditiv aduce un profit de 40$ , iar fiecare ton[ de solvent aduce un profit
de 30$.
Managementul firmei ABC, dup[ analiza cererii de pe pia[, a decis c[ preurile
stabilite vor determina v`nzarea ]ntregii cantit[ii produse (aditiv =i sovent).
Formularea problemei
Formularea problemei sau modelarea reprezint[ procesul de transpunere a problemei
]ntr-un model matematic. Modelarea problemei este o art[ care poate fi st[p`nit[ prin practic[
=i experien[. De=i fiecare problem[ are caracteristici unice, multe probleme pot avea
tr[s[turi comune. Ca urmare, pentru ]ncep[tori pot fi utile o serie de reguli ce pot fi aplicate
pentru formularea unui model, reguli ce vor fi ilustrate ]n dezvoltarea modelului matematic
pentru firma ABC.
Acest exemplu a fost selectat pentru a introduce metoda program[rii liniare pentru c[
este u=or de ]neles. }n practic[ apar probleme mai complicate, care necesit[ o analiz[ mai
profund[ pentru a identifica toate aspectele care trebuie incluse ]n model.
Primul pas este identificarea obiectivului =i a restriciilor. }n cazul nostru obiectivul
este maximizarea profitului total. Restriciile se refer[ la cantit[ile de materii prime
disponibile, care limiteaz[ cantit[ile de aditiv =i solvent ce pot fi produse.
Restricia 1: cantitatea de material 1 utilizat[ trebuie s[ fie mai mic[ sau egal[ cu
cantitatea de material 1 disponibil[.
Urm[torul pas este definirea variabilelor de decizie. Cele dou[ variabile de decizie
sunt: num[rul de tone de aditiv produse =i num[rul de tone de solvent produse. Not[m cu:
A: cantitatea de aditiv produs[ (tone)
S: cantitatea de solvent produs[ (tone)
A =i S sunt variabile de decizie.
Se scrie obiectivul utiliz`nd variabilele de decizie. Profitul total provine din dou[ surse:
v`nz[rile de aditiv =i v`nz[rile de solvent. Dac[ profitul obinut prin v`nzarea unei tone de
aditiv este de 40$, atunci prin v`nzarea a A tone profitul va fi 40*A. La fel, dac[ profitul
obinut prin v`nzarea unei tone de solvent este de 30$, atunci prin v`nzarea a S tone profitul
va fi 40*S.
Profitul total ˆ 40A ‡ 30S
Expresia matematic[ a obiectivului se nume=te funcie obiectiv. }n cazul nostru
obiectivul este maximizarea profitului total, deci funcia obiectiv va fi:


Max ( 40A ‡ 30S )
Se scriu restriciile utiliz`nd variabilele de decizie.
Restricia 1. Deoarece o ton[ de aditiv este produs[ folosind 2/5 tone de material 1,
cantitatea de material 1 necesar[ pentru a produce A tone de aditiv este 2/5 * A. Pentru fiecare
ton[ de solvent se folosesc ½ tone de material 1, deci cantitatea de material 1 necesar[
pentru a produce S tone de solvent este ½ * S. Astfel, cantitatea total[ de material 1 necesar[
este 2/5 * A ‡ ½ * S. Cantitatea disponibil[ de material 1 este de 20 tone, deci transpunerea
sub form[ de ecuaie a restriciei 1 este:
2
/5 * A ‡ ½ * S ˆ20
Restricia 2. Deoarece la fabricarea aditivului nu este necesar materialul 1 se va lua ]n
lua ]n calcul doar cantitatea de material 2 utilizat[ la fabricarea solventului. Pentru fiecare
ton[ de solvent se folosesc 1/5 tone de material 2, deci cantitatea de material 2 necesar[
pentru a produce S tone de solvent este 1/5 * S. Astfel, cantitatea total[ de material 2 necesar[
este 1/5 * S. Cantitatea disponibil[ de material 2 este de 5 tone, deci transpunerea sub form[
de ecuaie a restriciei 2 este:
1
/5 * S ˆ5
Restricia 3. Deoarece o ton[ de aditiv este produs[ folosind 3/5 tone de material 3,
cantitatea de material 3 necesar[ pentru a produce A tone de aditiv este 3/5 * A. Pentru fiecare
ton[ de solvent se folosesc 3/10 tone de material 3, deci cantitatea de material 3 necesar[
pentru a produce S tone de solvent este 3/10 * S. Astfel, cantitatea total[ de material 3
necesar[ este 3/5 * A ‡ 3/10 * S. Cantitatea disponibil[ de material 3 este de 21 tone, deci
transpunerea sub form[ de ecuaie a restriciei 3 este:
3
/5 * A ‡ 3/10 * S ˆ 21
P`n[ acum am specificat relaiile matematice referitoare la constr`ngerile asociate celor
trei materii prime. Mai trebuie oare alte restricii? Poate firma ABC s[ produc[ un num[r
negativ de tone de aditiv =i solvent? R[spunsul este evident nu. Deci pentru ca variabilele de
decizie s[ nu aib[ valori negative mai sunt necesare dou[ restricii:
A Žˆ0
S Žˆ0
Modelul matematic al problemei este acum complet. At`t obiectivul c`t =i restriciile au
fost transformate ]ntr-un set de relaii matematice, set de relaii definit ca model matematic.
Modelul matematic complet al problemei este:
Max ( 40A ‡ 30S )
2
/5 * A ‡ ½ * Sˆ20
1
/5 * Sˆ5
3
/5 * A ‡ 3/10 * Sˆ21
AŽˆ0
SŽˆ0
Pentru rezolvarea problemei trebuie g[sit[ combinaia optim[ (de A =i S) care s[
satisfac[ toate restriciile =i ]n acela=i timp s[ conduc[ la o valoare a funciei obiectiv care s[
fie mai mare sau egal[ dec`t orice valoare calculat[ cu o alt[ soluie posibil[.
Dac[ funcia obiectiv =i restriciile sunt funcii liniare ]n raport cu variabilele de
decizie (variabilele de decizie apar numai la puterea I), atunci avem o problem[ de
programare liniar[.

Pentru rezolvarea problemelor de programare liniar[ exist[ mai multe metode analitice:
metoda Simplex, metoda grafic[. }n continuare vom prezenta modul ]n care pot fi rezolvate
problemele de programare liniar[ utiliz`nd foile de calcul (Microsoft Excel).

13.5. Utilizarea foilor de calcul pentru rezolvarea problemelor de
programare liniară
Foile de calcul sunt instrumente utilizate frecvent pentru prelucrarea datelor ]n multe
organizaii. Deoarece modelele matematice necesit[ de multe ori date care deja exist[ ]n alte
foi de calcul, este important a ]nelege modul ]n care o problem[ de programare liniar[ poate
fi rezolvat[ cu ajutorul foilor de calcul. }n continuare vom ilustra modul ]n care se poate
rezolva problema precedent[ folosind foile de calcul. }n acest scop va fi folosit programul de
calcul tabelar Microsoft Excel.
Un model de programare liniar[ transpus ]ntr-o foaie de calcul va conine urm[toarele
elemente:
1. Celulele care conin datele problemei.
2. Celulele pentru variabilele de decizie.
3. O celul[ care conine formula pentru calcularea funciei obiectiv.
4. Celulele care conin formulele pentru calcularea p[rii st`ngi a restriciilor.
5. Celulele care conin valorile p[rii drepte a restriciilor.
Transpunerea problemei ]ntr-o foaie de calcul presupune parcurgerea urm[toarelor
etape:
1. Introducerea datelor problemei ]n foaia de calcul.
2. Definirea celulelor care vor conine variabilele de decizie.
3. Definirea celulei care conine formula pentru funcia obiectiv.
4. Definirea celulelor care conin formulele din partea st`ng[ a resticiilor.
5. Definirea celulelor care conin valorile din partea dreapt[ a restriciilor.
}n figura 13.2 este prezentat[ soluia pentru problema prezentat[ anterior.
A
1

B

C

D

Firma ABC

2
3
4
5
6
7
8

Materiale
Material 1
Material 2
Material 3
Profit pe tona

0.4
0
0.6
40

Necesar de materiale
Aditiv
Solvent
0.5
0.2
0.3
30

Cantitate disponibila
20
5
21

9
10
11

Model

12

Variabile de decizie
Aditiv
Solvent

13
14
15

Tone produse

16
17

Maximizarea profitului
total
=B8*B15+C8*C15

18

Restrictii
Material 1
Material 2
21
Material 3
22
19
20

Cantitati utilizate
=B5*B15+C5*C15
=B6*B15+C6*C15
=B7*B15+C7*C15

<=
<=
<=

Cantitati disponibile
=D5
=D6
=D7

Figura 13.2 – Foaia de calcul utilizat[ pentru rezolvarea problemei

Remarcai c[ foaia de calcul este alc[tuit[ din dou[ p[ri: o parte conine datele
problemei =i alta conine modelul. Un avantaj al separ[rii datelor de model este c[ se poate
studia efectul modific[rii m[rimilor de intrare asupra modelului f[c`nd modific[ri doar ]n
zona care conine date. Un alt avantaj este c[ analistul poate dezvolta modelul independent
de datele disponibile.
}n continuare este prezentat fiecare pas al procedurii:
Pasul 1: Introducerea datelor problemei. Datele problemei apar ]n partea superioar[ a
foii de calcul. Fraciile care reprezint[ compoziia pentru obinerea unei tone de solvent =i
aditiv au fost convertite ]n valori zecimale =i introduse ]n domeniul B5:C7. Valoarea 0.4 din
celula B5 arat[ c[ fiecare ton[ de aditiv produs[ utilizeaz[ 0.4 tone de material 1, valoarea
0.5 din celula C5 arat[ c[ fiecare ton[ de solvent produs[ utilizeaz[ 0.5 tone de material 1,
etc. Celulele D5:D7 conin cantitatea disponibil[ din fiecare material, iar celulele B8 =i C8
conin profitul obinut prin v`nzarea unei tone de aditiv (40$), respectiv solvent (30$).
Pasul 2: Definirea celulelor care vor conine variabilele de decizie. Celulele B15 =i
C15 conin num[rul de tone de aditiv =i solvent produse.
Pasul 3: Definirea celulei care conine formula funciei obiectiv. Celula B17 conine
formula pentru calcularea funciei obiectiv: ˆ B8*B15‡ C8*C15 (profiul unitar pe tona de
aditiv * producia de aditiv ‡ profiul unitar pe tona de solvent * producia de solvent).
Pasul 4: Definirea celulelor care conin formulele din partea st`ng[ a restriciilor.
Celulele B20:B22 conin formulele care indic[ cum se calculeaz[ partea st`ng[ a restriciilor.
Pentru materialul 1, ]n celula B20 se introduce formula ˆB5*B15‡C5*C15 (cantitatea de
aditiv produs[*cantitatea de material 1 pentru a produce o ton[ de aditv ‡ cantitatea de
solvent produs[*cantitatea de material 1 pentru a produce o ton[ de solvent). }n mod similar
se vor introduce ]n celulele B21 =i B22 formulele pentru materialele 2 =i 3.
Pasul 5: Definirea celulelor care conin valorile din partea dreapt[ a restriciilor. }n
problema analizat[ valorile din partea dreapt[ a restriciilor reprezint[ cantit[ile de material
disponibile, valori care deja sunt introduse ]n domeniul D5:D7. Pentru materialul 1, ]n celula
D20 se introduce formla ˆD5, pentru matrialul 2, ]n celula D21 se introduce formula ˆD6, iar
pentru materialul 3 ]n celula D22 se introduce formula ˆD7.
Un avantaj al folosirii foilor de calcul este c[ dac[ una din valorile din partea care
conine datele problemei se modific[, valorile din model se modific[ automat..
Pentru a determina soluia optim[ a problemei se va folosi Solver-ul din Excel. Pa=ii
urm[tori arat[ modul ]n care poate fi folosit Solver-ul pentru obinerea soluiei optime pentru
o problem[ de programare liniar[.
1. Se selecteaz[ meniul Tools.
2. Se aplic[ comanda Solver.
3. Caseta Solver Parameters se completeaz[ ]n modul urm[tor:
• Set Target Cell: B17
• Se selecteaz[ opiunea Max.
• By Changing Cells:
B15:C15.
4. Caseta Add Constraint se completeaz[ astfel:
• Cell Reference: B20:B22
• Se selecteaz[ operatorul ‹ ˆ

• Constraint: D20:D22
• Se selecteaz[ butonul OK.
5. C`nd caseta Solver Parameters apare din nou se selecteaz[ butonul Options.
6. }n caseta Solver Options se selecteaz[:
• Assume Linear Model.
• Assume Non- Negative.
• Butonul Ok.
7. C`nd caseta Solver Parameters apare din nou se selecteaz[ butonul Solve.
8. }n caseta Solver Results se selecteaz[ Keep Solver Solution. Se selecteaz[
butonul Ok pentru a genera soluia optim[, afi=at[ ]n celulele B15, C15.
Soluia optim[ este 25 tone de aditiv =i 20 tone de solvent.

13.6. Analiza de senzitivitate şi interpretarea rezultatelor
Problemele din lumea real[ au loc ]ntr-un mediu ]n continu[ schimbare. Preul
materiilor prime, salariile, cererea, oferta, valoarea aciunilor, etc. sunt valori care pot varia
de la un moment la altul. Dac[ o problem[ de programare liniar[ este utilizat[ ]ntr-un astfel
de mediu, ne putem a=tepta ca anumii coeficieni ai problemei s[ se modifice ]n timp. Deci
va trebui s[ determin[m cum afecteaz[ aceste schimb[ri soluia optim[ a problemei de
programare liniar[ iniial[.
Cu analiza de senzitivitate se poate observa cum este afectat[ soluia optim[ de
modific[ri ale coefiecienilor dintr-o problem[ de programare liniar[. Utiliz`nd analiza de
senzitivitate se poate r[spunde la ]ntreb[ri de tipul:
1. Cum este afectat[ soluia optim[ de o modificare a unui coeficient din funcia
obiectiv?
2. Cum este afectat[ soluia optim[ de o modificare a valorii din partea dreapt[ a
restriciilor?
Deoarece obiectul analizei de senzitivitate este modul ]n care modific[rile specificate
afecteaz[ soluia optim[, analiza nu poate ]ncepe p`n[ c`nd nu se obine soluia problemei de
programare liniar[ iniial[. Din aceast[ cauz[, analiza de senzitivitate este de multe ori
numit[ =i analiz[ postoptimal[.
Revenind la problema prezentat[ anterior:
Max ( 40A ‡ 30S )
2
/5 * A ‡ ½ * Sˆ20
1
/5 * Sˆ5
3
/5 * A ‡ 3/10 * Sˆ21
AŽˆ0
SŽˆ0

Materialul 1
Materialul 2
Materialul 3

Soluia optim[ Aˆ25 tone de aditiv =i Sˆ20 tone de solvent s-a obinut pentru cazul ]n
care s-a considerat c[ profitul pe ton[ pentru aditiv este 40$, iar profitul pe ton[ pentru
solvent este de 30$.
Presupunem c[ datorit[ unor factori exteriori are loc o reducere a preurilor, ceea ce
determin[ o sc[dere a profitului de la 30$ pe ton[ la 25$ pe ton[ pentru solvent. }n acest caz
programul de producie de 25 de tone de aditiv =i 20 de tone de solvent este ]n continuare cel
mai bun? }n mod normal ar trebui s[ rezolv[m o nou[ problem[ de programare liniar[ cu
funcia obiectiv modificat[ 40*A‡25*S. Acest lucru nu este necesar, deoarece cu analiza de
senzitivitate putem determina ]n ce limite poate varia profitul pe tona de aditiv f[r[ ca soluia

optim[ s[ se modifice. Dac[ analiza de senzitivitate arat[ c[ 25 tone de aditiv =i 20 de tone de
solvent r[m`ne soluia optim[ at`ta timp profitul pe tona de solvent variaz[ ]ntre 20$ =i 40$,
agentul decizional poate considera c[ estimarea de 30$/ton[ este bun[. Dac[ analiza de
senzitivitate arat[ c[ 25 de tone de aditiv =i 20 de tone de solvent r[m`ne soluia optim[ at`ta
timp profitul pe tona de solvent variaz[ ]ntre 29.90$ =i 32$, managementul va trebui s[
reanalizeze acurateea estim[rii de 30$/tona de solvent.
Domeniul de optimalitate pentru fiecare coeficient al funciei obiectiv este domeniul de
valori ]n care acest coeficient poate varia far[ a modifica soluia optim[. Managerul va trebui
s[ analizeze cu atenie acei coeficieni din funcia obiectiv care au un domeniu de
optimalitate ]ngust, deoarece o mic[ modificare a acestora poate modifica soluia optim[.
Un alt aspect al analizei de senzitivitate se refer[ la modific[rile valorilor din partea
dreapt[ a restriciilor. Referindu-ne la aceea=i problem[, pentru soluia optim[ sunt utilizate
]n ]ntregime stocurile de material 1 =i 3. Ce se ]nt`mpl[ cu soluia optim[ =i profitul total dac[
se m[resc cantit[ile disponibile de material 1 =i 3?
Cu analiza de senzitivitate se poate determina cu c`t va cre=te profitul total dac[
cantitatea disponibil[ de material 1 sau 3 cre=te cu o ton[.
Pentru ca programul Excel s[ furnizeze un raport pentru realizarea analizei de
senzitivitate, c`nd se rezolv[ problema cu Solver-ul, ]n fereastra de dialog Solver Results,
seciunea Reports, se selecteaz[ Sensitivity (vezi lecia 12).

13.7. Interpretarea raportului Excel pentru analiza de senzitivitate
Raportul generat de Excel are structura prezentat[ ]n figura 13.3.
Microsoft Excel 9.0 Sensitivity Report
Worksheet: Firma ABC
Report Created: 28/07/2001 12:39:34 PM

Adjustable Cells
Cell
Name
$B$15 Tone produse Aditiv
$C$15 Tone produse Solvent

Final
Value
25
20

Reduced
Cost

Objective Allowable Allowable
Coefficient Increase Decrease
0
40
20
16
0
30
20
10

Constraints
Cell
$B$20
$B$21
$B$22

Name
Material 1 Cantitati utilizate

Final
Shadow
Constraint Allowable Allowable
Value
Price
R.H. Side
Increase Decrease
20 33.33333333
20
1.5
6
4
0
5
1E+30
1
21 44.44444444
21
9
2.25

Figura 13.3 – Raportul de analiz[ de senzitivitate
Raportul are dou[ seciuni Adjustable Cells =i Constraints. }n seciunea Adjustable
Cells se analizeaz[ coeficienii variabilelor de decizie din funcia obiectiv, iar ]n seciunea
Constraints sunt analizate valorile din partea dreapt[ a restriciilor.
Seciunea Adjustable Cells
}n coloana Cell sunt afi=ate celulele care conin coeficienii variabilelor de decizie din
funcia obiectiv, iar ]n coloana Name sunt afi=ate numele acestor celule.
Coloana Final Value conine valorile optime pentru variabilele de decizie. Pentru
problema analizat[ soluia este 25 de tone de aditiv =i 20 tone de solvent.
Coloana Reduced Cost. Pentru fiecare variabil[ de decizie, valoarea absolut[ din
Reduced Cost arat[ c`t de mult trebuie s[ creasc[ (pentru problemele de maximizare) sau s[

scad[ (pentru problemele de minimizare) coeficientul variabilei de decizie din funcia
obiectiv astfel ]nc`t variabila de decizie respectiv[ s[ aib[ valoare pozitiv[. Dac[ o variabil[
de decizie este pozitiv[ ]n soluia optim[, costul redus este 0. Pentru problema analizat[
ambele variabile de decizie au valori pozitive =i costurile reduse sunt 0. Dac[ de exemplu
pentru cantitatea de solvent s-ar fi obinut 0 ]n coloana Final Value =i –12.5 ]n coloana
Reduced Cost, interpretarea ar fi urm[toarea: profitul pe tona de solvent ar trebui s[ creasc[
la 30‡12.50ˆ42.50 pentru ca ]n soluia optim[ variabila de decizie ata=at[ cantit[ii de
solvent s[ aib[ o valoare pozitiv[. Altfel spus, pentru a produce solvent ar trebui ca profitul
pe tona de solvent s[ fie 42.50$.
Coloana Objective Coefficient conine valorile coeficienilor variabilelor de decizie
din funcia obiectiv, iar coloanele Allowable Increase =i Allowable Decrease conin valorile
pe baza c[rora se poate calcula domeniu de optimalitate pentru coeficientul respectiv
(cre=terea =i mic=orarea permis[). De exemplu, pentru aditiv:
40 − 16 ≤ C Aditiv ≤ 40 + 20
24 ≤ C Aditiv ≤ 60
Deci dac[ profitul pe tona de aditiv variaz[ ]ntre 24 =i 60, soluia optim[ de 25 tone de
aditiv =i 20 tone de solvent r[m`ne neschimbat[.
Pentru solvent:
30 − 10 ≤ CSolvent ≤ 30 + 20
20 ≤ CSolvent ≤ 50
Deci dac[ profitul pe tona de solvent variaz[ ]ntre 20 =i 50, soluia optim[ de 25 tone de
aditiv =i 20 tone de solvent r[m`ne neschimbat[.
Seciunea Constraints
Coloana Cell indic[ celulele care conin valorile din partea dreapt[ a restriciilor, iar
coloana Name conine numele acestor celule.
Valorile din coloana Final Value sunt valorile restriciilor (partea st`ng[) calculate
pentru soluia optim[. Pentru problema analizat[ valorile din coloana Final Value indic[
cantit[ile de material 1, 2 =i 3 necesare pentru a produce combinaia optim[ de 25 de tone de
aditiv =i 20 tone de solvent. Deci pentru soluia optim[ sunt necesare 20 tone de material 1, 4
tone de material 2 =i 21 tone de material 3.
Valorile din coloana Constraint RH sunt valorile iniiale ale problemei: 20 tone de
material 1, 5 tone de material 2, 21 tone de material 3 (cantit[ile disponibile). Pentru fiecare
restricie abaterea reprezint[ diferena dintre valoarea din coloana Constraint RH =i
valoarea din Final Value. Abaterea asociat[ materialului 1 este 20-20ˆ0 tone, pentru
materialul 2: 5-4ˆ1 ton[, iar pentru materialul 3: 21-21ˆ0 tone. Deci materialele 1 =i 3 sunt
utilizate ]n totalitate, iar din materialul 2 r[m`ne o ton[. Concluzia este c[ dac[ ar exista
cantit[i mai mari de material 1 sau 3 s-ar putea obine un profit total mai mare. Modul ]n
care modificarea acestor cantit[i influeneaz[ profitul este indicat ]n coloana Shadow Price
(preuri umbr[).
Preurile umbr[ arat[ cu c`t se modific[ (cre=tere/mic=orare) valoarea funciei obiectiv
la cre=terea/mic=orarea cu o unitate a valorii din partea dreapt[ a unei restricii.
}n cazul nostru, preul umbr[ de 33.33 pentru materialul 1 arat[ c[ o ton[ suplimentar[
de material 1 va cre=te profitul cu 33.33$. Deci, dac[ cantitatea disponibil[ de material 1 ar
cre=te de la 20 la 21, ceilali coeficieni r[m`n`nd constani, profitul total ar cre=te cu 33.33$,
ceea ce ]nseamn[ 1600‡33.33ˆ1633.33$.
Similar, dac[ cantitatea disponibil[ de material 3 ar cre=te de la 21 la 22, ceilali
coeficieni r[m`n`nd constani, profitul total ar cre=te cu 44.44$, ceea ce ]nseamn[
1600‡44.44ˆ1644.44$.

Valoarea 0 a preului umbr[ pentru materialul 2 arat[ c[ dac[ cantitatea disponibil[ de
material 2 ar cre=te, valoarea funciei obiectiv (profitul total) nu s-ar modifica.
Ultimele dou[ coloane Allowable Increase =i Allowable Decrease determin[ domeniul
]n care poate varia termenul din dreapta al unei restricii f[r[ a se modifica preurile umbr[.
De exemplu, consider`nd restricia pentru materialul 1, termenul din partea dreapt[ are
valoarea 20, cre=terea permis[ este 1.5 =i mic=orarea permis[ este de 6. +tim c[ cu un pre
umbr[ de 33.33$ , o ton[ ]n plus de material 1 va cre=te valoarea funciei obiectiv (profitul)
cu 33.33$, iar reducerea cantit[ii de material cu o ton[ va mic=ora valoarea funciei obiectiv
cu 33.33$. Valorile din Allowable Increase =i Allowable Decrease arat[ c[ preul umbr[ de
33.33$ este valabil pentru cre=teri de material 1 de p`n[ la 1.5 tone =i reduceri de pan` la 6
tone.
Domeniul de valori ]n care preul umbr[ este aplicabil se nume=te domeniu de
fezabilitate. Deci pentru materialul 1 domeniul de fezabilitate este ]ntre 20-6ˆ14 =i
20‡1.5ˆ21.5 tone. Pentru modific[ri ]n afara domeniului de fezabilitate problema trebuie
rezolvat[ din nou pentru a g[si noul pre umbr[.
Pentru restricia materialului 2 cre=terea permis[ este 1E‡30, deci 1030, un num[r foarte
mare. Putem interpreta aceast[ valoare ca o eviden[ a faptului c[ nu exist[ limit[ superioar[
pentru domeniul de fezabilitate a materialului 2. Cu alte cuvinte, oric`t material 2 ar fi
disponibil, valoarea funciei obiectiv nu s-ar modifica. Descre=terea permis[ (1) arat[ c[
limita minim[ a domeniului de fezabilitate pentru materialul 2 este 5-1ˆ4 tone. Deci dac[
pentru producie ar fi disponibile 4.5 tone de material 2, valoarea funciei obiectiv nu s-ar
modifica. Dac[ sunt disponibile mai puin de 4 tone va trebui s[ rezolv[m problema din nou
pentru a afla noua soluie =i preurile umbr[.
Pentru materialul 3, domeniul de fezabilitate este ]ntre 21-2.25ˆ18.75 tone =i 21‡9ˆ30
tone. Deci preul umbr[ de 44.44 este aplicabil dac[ termenul din partea dreapt[ a restriciei
(cantitatea de material disponibil) ia valori ]ntre 18.75 tone =i 30 tone.
Informaiile din raportul de analiz[ de senzitivitate se bazeaz[ pe presupunerea c[ doar
un coeficient se modific[, toi ceilali r[m`n`nd neschimbai.

Rezolvarea problemelor de transport

CAPITOLUL 14
REZOLVAREA PROBLEMELOR DE TRANSPORT
14.1. Probleme de transport
Problemele de transport apar frecvent ]n situaiile ]n care trebuie planificat modul de
distribuire al bunurilor de la produc[tori la consumatori. Obiectivul obi=nuit al acestor
probleme este minimizarea costurilor de transport. Modelele de transport sunt o variaie a
problemelor de programare liniar[ =i presupun urm[toarele:
1. Obiectivul este minimizarea costurior totale de transport.
2. Costurile de transport sunt funcii liniare ]n raport cu num[rul de unit[i
transportate.
3. Cererea =i oferta sunt exprimate ]n unit[i omogene.
4. Costurile de transport pe unitate nu variaz[ cu cantitatea transportat[.
Pentru a ilustra modul ]n care se pot rezolva problemele de transport prezent[m
urm[torul exemplu:
O companie dispune de trei fabrici =i patru centre de distribuie. Fabricile sunt plasate
]n Cluj, Bac[u =i Craiova. Capacit[ile de producie ale fabricilor sunt:
Fabrica
Capacitate de producie (unit[i)
Cluj
5000
Bac[u
6000
Craiova
2500
Total:
13.500
Centrele de distribuie sunt plasate ]n Deva, Ia=i, Bucure=ti, Bra=ov. Cererea pentru
produsele companiei ]n aceste centre este:
Centre de distribuie
Cerere (unit[i)
Deva
6000
Ia=i
4000
Bucure=ti
2000
Bra=ov
1500
Total:
13.500
Managementul ar dori s[ determine cantitatea care ar trebui transportat[ de la fiecare
fabric[ la fiecare centru de distribuie astfel ]nc`t costurile de transport s[ fie minime.
Figura 14.1 prezint[ graficul cu cele 12 rute posibile. Un astfel de graf este numit graf
de reea. Cercurile reprezint[ nodurile reelei. Liniile care unesc nodurile se numesc arcuri.
Fiecare punct de plecare =i sosire este reprezentat printr-un nod, iar fiecare rut[ posibil[ este
reprezentat[ printr-un arc. }n dreptul fiec[rui nod este trecut[ valoarea ofertei (pentru
capacit[ile de producie) sau a cererii (pentru centrele de distribuie). Sensul de deplasare
este indicat prin s[gei. Costurile unitare de transport pentru fiecare rut[ sunt prezentate ]n
tabelul 14.1 =i pe fiecare arc din figura 14.1.
Destinaie
Origine
1. Deva
2. Ia=i
3. Bucure=ti
4. Bra=ov
1. Cluj
3
2
7
6
2. Bac[u
7
5
2
3
3. Craiova
2
5
4
5
Tabelul 14.1 – Costurile unitare de transport pe fiecare rut[


Deva

5000

4000

Bucure=ti

2000

Bra=ov

1500

2

7
Bac[u

7

5
2

3

2
2500

Ia=i

3

Cluj

6

6000

6000

Craiova

5
4

5

Figura 14.1 – Graful de reea ata=at problemei
Pentru a rezolva problema de transport putem folosi programarea liniar[. Vom utiliza
variabile de decizie cu doi indici, primul indice indic[ nodul origine, al doilea nodul
destinaie. Astfel xij indic[ num[rul de unit[i transportate de la fabrica i la centrul de
distribuie j.
Costul unit[ilor transportate din Cluj este
ˆ 3*x11‡2*x12‡7*x13‡6*x14
Costul unit[ilor transportate din Bac[u este ˆ 7*x21‡5*x22‡2*x23‡3*x24
Costul unit[ilor transportate din Craiova este ˆ 2*x31‡5*x32‡4*x33‡5*x34
Suma acestor costuri este costul total de transport, valoare care trebuie minimizat[, deci
funcia obiectiv este:
Min (3*x11‡2*x12‡7*x13‡6*x14‡7*x21‡5*x22‡2*x23‡3*x24‡2*x31‡5*x32‡4*x33‡5*x34)
}n problemele de transport apar restricii deoarece fiecare fabric[ are o capacitate de
producie limitat[ =i fiecare centru de distribuie are o anumit[ cerere. Fabrica din Cluj are o
capacitate de producie de 5000 unit[i. Num[rul total de unit[i transportate din fabrica de la
Cluj este x11‡x12‡x13‡x14, deci restricia asociat[ acestei fabrici este:
x11‡x12‡x13‡x14 ≤ 5000
}n mod similar pentru celelalte fabrici avem:
x21‡x22‡x23‡x24 ≤ 6000 - pentru fabrica de la Bac[u.
x31‡x32‡x33‡x34 ≤ 2500 - pentru fabrica de la Craiova.
}n cele patru centre de distribuie, restricia va fi dat[ de faptul c[ cererea la centrul
respectiv trebuie s[ fie egal[ cu cantit[ile transportate aici.
x11‡x21‡x31‡x41 ˆ6000 - cererea la Deva
x12‡x22‡x32‡x42 ˆ4000 - cererea la Ia=i
x13‡x23‡x33‡x43 ˆ2000 - cererea la Bucure=ti

x14‡x24‡x34‡x44 ˆ1500 - cererea la Bra=ov
Combin`nd funcia obiectiv cu restriciile obinem modelul pentru problema de
transport:
Min (3*x11‡2*x12‡7*x13‡6*x14‡7*x21‡5*x22‡2*x23‡3*x24‡2*x31‡5*x32‡4*x33‡5*x34)
x11‡x12‡x13‡x14 ≤ 5000
x21‡x22‡x23‡x24 ≤ 6000
x31‡x32‡x33‡x34 ≤ 2500
x11‡x21‡x31‡x41 ˆ6000
x12‡x22‡x32‡x42 ˆ4000
x13‡x23‡x33‡x43 ˆ2000
x14‡x24‡x34‡x44 ˆ1500
xij≥0, iˆ1,2,3; jˆ1,2,3,4

14.2. Rezolvarea problemei în Excel
Foaia de calcul folosit[ pentru rezolvarea problemei este prezentat[ ]n figura 14.2.
A
1

B

C

D

E

F

G

H

Modelarea problemelor de transport

2
3
4
5
6
7
8

Origine
Cluj
Bacau
Craiova
Cerere

Deva
3
7
2
6000

Destinatie
Iasi
Bucuresti
2
7
5
2
5
4
4000
2000

Oferta
6
5000
3
6000
5
2500
1500

Brasov

9
10
11

Model

12

Cost minim

13

39500

14
15
16
17
18
19
20
21
22

Origine
Cluj
Bacau
Craiova
Total

Deva
3500
0
2500
6000
=
6000

Destinatie
Iasi
Bucuresti
1500
0
2500
2000
0
0
4000
2000
=
=
4000
2000

Brasov
0
1500
0
1500
=
1500

Total
5000
6000
2500

<=
<=
<=

5000
6000
2500

Figura 14.2 – Foaia de calcul ata=at[ problemei
Datele problemei sunt introduse ]n domeniul A1:F8. Costurile de transport sunt
coninute ]n domaniul B5:E7, capacit[ile de producie (oferta) ]n F5:F7, iar cererea din
centrele de distribuie ]n celulele B8:E8.
Elementele cheie care trebuie introduse ]n Excel sunt variabilele de decizie, funcia
obiectiv, partea st`ng[ =i partea dreapt[ a restriciilor.

Variabilele de
decizie

Celulele B17:E19 conin variabilele de decizie. Iniial toate
variabilele de decizie au valoarea 0.

Funcia
obiectiv

Pentru a calcula costul total, ]n celula C13 a fost introdus[ formula
ˆSUMPRODUCT(B5:E7,B17:E19).

Partea st`ng[ a
restriciilor

Celulele F17:F19 conin formulele pentru partea st`ng[ a
restriciilor asociate capacit[ilor de producie, iar
celulele
B20:E20 conin formulele pentru partea st`ng[ a restriciilor
asociate cererii din centrele de distribuie. Formulele utilizate sunt:
Celula F17: ˆSUM(B17:E17). Se copieaz[ F17 ]n F18:F19.
Celula B20: ˆSUM(B17:B19). Se copieaz[ B20 ]n C20:E20.

Partea dreapt[
a restriciilor

Celulele H17:H19 conin partea dreapt[ a restriciilor asociate
capacit[ilor de producie, iar celulele B22:E22 conin partea
dreapt[ a restriciilor asociate cererii din centrele de distribuie.
Aceste valori sunt introduse deja ]n datele iniiale ale problemei,
deci se vor utiliza formulele:
Celula H17: ˆF5. Se copieaz[ H17 ]n H18:H19.
Celula B22: ˆB8. Se copieaz[ B22 ]n C22:E22.

Se rezolv[ problema utiliz`nd Solver-ul. Caseta de dialog Solver Parameters se
completeaz[ ca ]n figura 14.3. Opiunile selectate sunt Assume Linear Model =i Assume
Non-Negative.

Figura 14.3 – Caseta de dialog Solver
Soluia optim[ arat[ c[ costul minim de transport este de 39500 u.m., iar ]n domeniul
B17:E19 sunt afi=ate cantit[ile care trebuie transportate pe fiecare rut[. Valoarea 0 indic[ c[
pe ruta respectiv[ nu se transport[ nimic.

14.3. Variaţii ale problemelor de transport
Oferta totala nu este egala cu cererea totala
}n multe cazuri oferta total[ nu este egal[ cu cererea total[. Dac[ oferta total[ dep[=e=te
cererea total[ nu este necesar[ nici o modificare ]n problema de programare liniar[. Excesul

de ofert[ va ap[rea ca o abatere ]n soluia problemei, iar aceste abateri pot fi interpretate ca
ofert[ neutilizat[ sau cantit[i netransportate.
Dac[ oferta total[ este mai mic[ dec`t cererea total[ modelul de programare liniar[ a
problemei de transport nu are o soluie fezabil[. Pentru rezolvarea problemei se creeaz[ o
ofert[ fictiv[ astfel ]nc`t excesul de cerere s[ fie satisf[cut =i se atribuie costurilor de
transport din acest punct valoarea 0. }n acest mod problema de programare liniar[ va avea
soluie.
Maximizarea functiei obiectiv
}n unele probleme obiectivul este g[sirea unei soluii care maximizeaz[ venitul sau
profitul. Utiliz`nd venitul sau profitul unitar ]n coeficienii funciei obiectiv, se va rezolva o
problem[ de maximizare ]n locul uneia de minimizare. Modific[rile nu afecteaz[ restriciile.
Rute neacceptate
Stabilirea unei rute de la fiecare nod origine la fiecare nod destinaie nu este
]ntotdeauna posibil[. Pentru a rezolva aceste situaii se elimin[ din graful de reea arcele
respective, iar din modelul de programare liniar[ variabilele de decizie corespunz[toare.
Pentru a face c`t mai puine modific[ri ]n foaia de calcul, pentru aceste rute se stabilesc
costuri foarte mari, astfel ]nc`t pe aceste rute se vor efectua transporuri doar dac[ nu exist[
alte soluii fezabile.
Rute cu capacitati limitate
Pentru rutele cu capacit[i limitate se introduc restricii suplimentare. De exemplu, dac[
mijloacele de transport pe ruta Craiova – Deva nu pot transporta mai mult de 1000 de unit[i
se va introduce restricia x13≤1000.
Modelul general de programare liniar[ al unei probleme de transport cu m puncte de
origine =i n puncte de destinaie este:
m

Min

n

∑∑c
i =1 j =1
n

ij

x ij

∑

x ij ≤ s i

∑

x ij = d

j =1
m

i =1

x ij ≥ 0

i = 1, 2 ,..., m
j

Oferta

j = 1, 2 ,..., n

Cererea

pentru toti i si j

unde:
i ˆ index-ul pentru punctele de origine
j ˆ index-ul pentru punctele de destinaie
xij ˆ num[rul de unit[i transportate de la originea i la destinaia j
cij ˆ costul unitar de transport din originea i la destinaia j
si ˆ oferta sau capacitatea din originea i
dj ˆ cererea la destinaia j

Rezolvarea problemelor de alocare

CAPITOLUL 15
REZOLVAREA PROBLEMELOR DE ALOCARE
15.1. Probleme de alocare
Problemele de alocare pot ap[rea ]n diverse situaii de luare a deciziilor. Problemele
tipice sunt: alocarea lucr[rilor pe ma=ini, repartizarea personalului ]n diverse centre
teritoriale, repartizarea agenilor care s[ efectueze anumite activit[i. O caracteristic[ distinct[
este c[ unui agent ]i este asignat[ o singur[ activitate =i se ]ncearc[ optimizarea unui obiectiv,
cum ar fi minimizarea costurilor, minimizarea timpului, maximizarea profitului, etc.
Pentru a ilustra modul de rezolvare a problemelor de alocare vom considera urm[torul
exemplu: Firma ABC, specializat[ ]n studii de marketing are trei clieni noi. Fiec[rui proiect
]i trebuie alocat un lider de proiect. Timpul necesar pentru realizarea proiectului depinde de
experiena =i abilitatea liderului de proiect. }n prezent sunt disponibile doar trei persoane,
proiectele au aproximativ aceea=i prioritate =i nu pot fi realizate ]n acela=i timp. Conducerea
firmei trebuie s[ stabileasc[ ce lider de proiect va coordona fiecare studiu astfel ]nc`t cele trei
studii s[ se termine ]n timpul total cel mai scurt. Unui lider i se poate aloca doar un proiect.
Cu trei clieni =i trei studii sunt posibile 9 alternative. Timpii estimai pentru finalizarea
fiec[rui proiect sunt prezentai ]n tabelul 15.1.
Client
Lider de proiect
1
2
3
Ionescu
10
15
9
Popescu
9
18
5
Georgescu
6
14
3
Tabelul 15.1 – Timpii estimai pentru terminarea fiec[rui proiect
Figura 15.1 prezint[ graful de reea pentru problema analizat[.

1

Client
1

1

Client
2

10

1
Ionescu

1

Client
3

1

15
9
9
1

2
Popescu

18
5

6
1

3
Georgescu

14
3

Figura 15.1 – Graful de reea ata=at problemei


Nodurile corespund liderilor de proiect =i clienilor, iar arcurile reprezint[ repartiz[rile
posibile ale liderilor de proiect clienilor.
Oferta ]n fiecare nod origine este 1 =i cererea ]n fiecare nod destinaie este 1. Costul
repartiz[rii unui lider de proiect la un client este timpul necesar pentru realizarea studiului.
Observai asem[narea dintre problemele de alocare =i cele de transport, problemele de alocare
fiind un caz special de probleme de transport ]n care toate ofertele =i cererile au valoarea 1,
iar cantitatea transportat[ pe fiecare arc este 0 sau 1.
Problema poate fi rezolvat[ folosind metoda program[rii liniare. Avem nevoie de o
variabil[ pentru fiecare arc =i o restricie pentru fiecare nod. Vom utiliza variabile de decizie
cu doi indici xij - repartizarea liderului i la proiectul j.
Deci vom avea 9 variabile de decizie:
1, daca liderul i este repartizat clientului j
xij = 
0, in celelalte cazuri
unde iˆ1,2,3 =i jˆ1,2,3.
Utiliz`nd aceste notaii:
Timpul necesar pentru finalizarea proiectelor de c[tre Ionescu este 10x11‡15x12‡9x13
(doar una din variabilele de decizie poate lua valoarea 0).
Timpul necesar pentru finalizarea proiectelor de c[tre Popescu este 9x21‡18x22‡5x23
Timpul necesar pentru finalizarea proiectelor de c[tre Georgescu este 6x31‡14x32‡3x33
Suma acestor timpi furnizeaz[ num[rul total de zile pentru a finaliza cele trei studii de
pia[. Astfel, funcia obiectiv este:
Min (10x11‡15x12‡9x13‡9x21‡18x22‡5x23‡6x31‡14x32‡3x33)
Restriciile reflect[ faptul c[ fiecare lider poate fi repartizat cel mult unui client =i
fiecare client trebuie s[ aib[ repartizat un lider. Aceste restricii sunt:
x11 + x12 + x13 ≤ 1
− repartizarea lui Ionescu
x21 + x22 + x23 ≤ 1 − repartizarea lui Popescu
x31 + x32 + x33 ≤ 1 − repartizarea lui Georgescu
x11 + x21 + x31 = 1
− clientul 1
x12 + x22 + x32 = 1
− clientul 2
x13 + x23 + x33 = 1
− clientul 3
Combin`nd funcia obiectiv cu restriciile obinem urm[torul model:
Min (10x11‡15x12‡9x13‡9x21‡18x22‡5x23‡6x31‡14x32‡3x33)
x11 + x12 + x13 ≤ 1
− repartizarea lui Ionescu
x21 + x22 + x23 ≤ 1 − repartizarea lui Popescu
x31 + x32 + x33 ≤ 1 − repartizarea lui Georgescu
x11 + x21 + x31 = 1
− clientul 1
x12 + x22 + x32 = 1
− clientul 2
x13 + x23 + x33 = 1
− clientul 3
xij ≥ 0

pentru i = 1,2,3; j = 1,2,3

Foaia de calcul folosit[ pentru rezolvarea problemei este prezentat[ ]n figura 15.2.
A
1

B

C

D

E

F

G

Firma ABC

2

Client
2

3

Lider de proiect
5 Ionescu
6 Popescu
7 Georgescu
4

1
10
9
6

3
15
18
14

9
5
3

8
9
10

Model

11

Timp de realizare a
proiectului

12

26

13

Client
2

14
15
16
17
18
19

Lider de proiect
Ionescu
Popescu
Georgescu
Total

20
21

1
0
0
1
1
=

3
1
0
0
1

=
1

Total
0
1
0
1

1
1
1

<=
<=
<=

1
1
1

=
1

1

Figura 15.2 – Foaia de calcul ata=ata problemei
Datele problemei sunt introduse ]n domeniul A1:D7.
Variabilele de
decizie

Celulele D16:D18 sunt rezervate variabilelor de decizie. Iniial
toate variabilele de decizie au valoarea 0.

Funcia
obiectiv

Formula ˆSUMPRODUCT(B5:D7,B16:D18) a fost plasat[ ]n
celula C12 pentru a calcula num[rul necesar de zile pentru a
termina toate proiectele.
Celulele E16:E18 conin partea st`ng[ a restriciilor referitoare la
num[rul de clieni la care poate fi repartizat un lider. Celulele
B19:D19 conin partea st`ng[ a restriciilor conform c[rora unui
proiect trebuie s[-i fie repartizat un lider de proiect. Formulele
utilizate sunt:
Celula E16: ˆSUM(B16:D16). Se copieaz[ E16 ]n E17:E18.
Celula B19: ˆSUM(B16:B18). Se copieaz[ B19 ]n C19:D19.
Celulele G16:G18 conin partea dreapt[ a restriciilor pentru lideri,
iar celulele B21:D21 conin partea dreapt[ a restriciilor pentru
clieni. Toate valorile sunt egale cu 1.

Partea st`ng[ a
restriciilor

Partea dreapt[
a restriciilor

Se rezolv[ problema utiliz`nd Solver-ul. Caseta de dialog Solver Parameters se
completeaz[ ca ]n figura 15.3. Opiunile selectate sunt Assume Linear Model =i Assume
Non-Negative.

Figura 15.3 – Caseta Solver Parameters
Soluia optim[ a problemei este: Ionescu este repartizat clientului 2, Popescu clientului
3 =i Georgescu clientului 1. Timpul de finalizare a celor trei proiecte este de 26 de zile.

15.2. Variaţii ale problemei
Deoarece problemele de alocare pot fi tratate ca fiind cazuri speciale de probleme de
transport, variaiile care pot ap[rea la problemele de alocare sunt acelea=i ca =i la problemele
de transport.
Num[rul total de ageni (oferta) este diferit de num[rul total de activit[i (cererea)
Dac[ num[rul de ageni dep[=e=te num[rul de activit[i, agenii suplimentari vor
r[m`ne nealocai ]n modelul de programare liniar[. Dac[ num[rul de activit[i este mai mare
dec`t num[rul de ageni, modelul de programare liniar[ nu va avea o soluie fezabil[. }n
aceast[ situaie este suficient s[ ad[ug[m un num[r suficient de „ageni fal=i“ pentru ca
num[rul de ageni s[ fie egal cu num[rul de activit[i. }n funcia obiectiv coeficienii pentru
agenii fal=i vor fi zero.
Dac[ problemele de alocare sunt evaluate ]n termeni de venit sau profit vom avea de
rezolvat o problem[ de maximizare ]n loc de una de minimizare.
}n plus, dac[ una sau mai multe aloc[ri nu pot fi acceptate, variabilele de decizie
corespunz[toare vor fi eliminate din modelul de programare liniar[. Pentru exemplul
prezentat acest lucru poate ap[rea dac[ la un agent nu are experiena necesar[ s[ lucreze la un
proiect. Pentru a nu face modific[ri ]n foaia de calcul, cea mai simpl[ soluie ar fi ata=area
unor costuri foarte mari pentru variabilele de decizie ce corespund aloc[rilor ce nu pot fi
acceptate.
Modelul general pentru problemele de alocare este:

m

Min

n

∑∑c
i =1 j =1
n

ij

x ij

∑

x ij ≤ 1

i = 1, 2 ,..., m

Agenti

∑

x ij = 1

j = 1, 2 ,..., n

Activitati

x ij ≥ 0

pentru toti i si j

j =1
m

i =1

Managementul proiectelor

CAPITOLUL 16
MANAGEMENTUL PROIECTELOR
16.1. Managementul proiectelor
Multe din proiectele din viaa real[ sunt foarte complexe =i costisitoare. Realizarea
acestora la timp =i ]n cadrul bugetului alocat nu este o sarcin[ u=oar[. }n mod tipic, anumite
activit[i nu pot ]ncepe ]nainte ca altele s[ se termine. Iar dac[ ]ntr-un proiect apar sute de
astfel de dependene, problemele de planificare se complic[ foarte mult, iar managerii au
nevoie de metode speciale de analiz[.
C`teva din ]ntreb[rile la care vom ]ncerca s[ r[spundem ]n continuare sunt:
1. Care este termenul de terminare al proiectului?
2. Care sunt momentele de ]nceput =i de terminare ale fiec[rei activit[i?
3. Care activit[i sunt critice, ]n sensul c[ ele trebuie s[ se termine exact ]n termenul
planificat, astfel ]nc`t s[ nu fie dep[=it termenul final de realizare al proiectului?
4. C`t de mult pot fi ]nt`rziate activit[ile necritice astfel ]nc`t s[ nu fie dep[=it
termenul final de realizare al proiectului?
5. Cum pot fi alocate resursele diverselor activit[i astfel ]nc`t proiectul s[ se realizeze
rapid =i cu costuri minime?
Metodele PERT =i CPM, acronimele pentru Program Evaluation Review Technique =i
Critical Path Method, graficele Gant, sunt metode de analiz[ utilizate pentru managemenul
proiectelor. Indiferent de metod[, primul pas ]n planificarea proiectelor este definirea
activit[ilor =i stabilirea relailor de preceden[ dintre acestea. Aceasta este partea cea mai
important[ a unui proiect =i ]n mod normal ]n aceast[ etap[ ar trebui implicate mai multe
persoane, astfel ]nc`t s[ nu fie uitat[ nici o activitate important[.
Exemplu
}n prezent firma ABC are birouri doar ]n Bucure=ti, =i dore=te s[ deschid[ birouri noi ]n
Bra=ov. }n acest scop o parte din personalul din Bucure=ti se va muta ]n Bra=ov =i se va
angaja personal nou. }n timp ce economi=tii trebuie s[ se ocupe de partea financiar[ a
afacerii, arhitecii trebuie s[ se ocupe de proiectarea interioarelor.
Anumite p[ri ale proiectului nu pot ]ncepe p`n[ c`nd altele nu sunt terminate. De
exemplu, nu pot fi amenajate birourile dac[ acestea nu au fost ]nc[ proiectate, sau nu se poate
angaja personal p`n[ nu se stabile=te personalul necesar. }n tabelul 16.1 sunt prezentate
activit[ile din care este alc[tuit proiectul.
Activitatea

Descriere

A
B

Selectarea birourilor
Stabilirea planului de organizare =i a
celui financiar
Determinarea personalului necesar
Proiectarea interioarelor
Amenajarea birourilor
Selectarea personalului care se va muta
Angajarea de personal nou
Mutarea propriu-zis[

C
D
E
F
G
H

Activit[i
precedente
-

Durata de realizare
(s[pt[m`ni)
3
5

B
A, C
D
C
F
F

3
4
8
2
4
2

I

Stabilirea relaiilor cu noii parteneri din
Bra=ov
Instruirea peronalului

J

B

5

H, E, G

3

Tabelul 16.1 - Activit[ile proiectului
Fiecare activitate este plasat[ ]ntr-un r`nd separat, iar ]n coloana Activit[i precedente
sunt trecute activit[ile care trebuie realizate ]naintea ]nceperii activit[ii analizate. De
exemplu activitatea C nu poate ]ncepe p`n[ nu se termin[ activitatea B. }n coloana Durata de
realizare este trecut timpul estimat pentru realizarea activit[ilor.

16.2. Grafice Gant
Una din metodele cele mai populare folosite pentru planificarea proiectelor este
utilizarea graficelor Gant. Fiecare activitate este desf[=urat[ pe axa vertical[. Pe axa
orizontal[ este reprezentat timpul. Activit[ile sunt reprezentate prin bare de lungime egal[ cu
timpul de realizare a activit[ii. Graficul indic[ =i termenul cel mai devreme de ]ncepere a
fiec[rei activit[i. De exemplu, activitatea C nu poate ]ncepe ]nainte de sf`r=itul s[pt[m`nii 5,
deoarece activitatea B trebuie s[ se termine ]nainte ca C s[ ]nceap[. Pe m[sur[ ce o activitate
este realizat[, bara asociat[ este ha=urat[. Astfel, ]n orice moment de timp este foarte clar ce
activit[i au fost realizate la timp =i care nu. Graficul din figura 16.1 arat[ c[ ]n s[pt[m`na 13
activit[ile D, E =i H sunt ]n urma planului, iar activitatea G este ]naintea planului.

A

3
5

B

3

C
D

4

E

8

2

F

4

G
H

2

5

I
J

3

0

2

4

6

8

10

12

14

16

18

20

22

Figura 16.1 – Graficul Gant
}n contextul graficelor Gant „]n plan“ ]nseamn[ c[ activitatea nu a fost finalizat[ mai
t`rziu de cel mai devreme termen de terminare a activit[ii. Astfel, ]n figura 16.1 putem
observa c[ activit[ile D =i H ar trebui s[ se termine cel mai devreme ]n s[pt[m`na 12.
Deoarece nu sunt terminate ]n s[pt[m`na 13 ele sunt ]n urma planului.
Din graficele Gant nu se pot stabili predecesorii imediai ai unei activit[i. }n figura
16.1 poate p[rea c[ F =i I sunt activit[i precedente ale activit[ii G, deoarece G poate ]ncepe
]n s[pt[m`na 10, iar F =i I se pot termina atunci. Dar din tabelul 16.1 =tim c[ doar F este

„predecesor imediat“ a lui G. O ]nt`rziere a activit[ii I nu ar afecta momentul de ]ncepere al
activit[ii G. Astfel de informaii sunt importante pentru manager pentru c[ ar putea s[
stabileasc[ ce activit[i ar putea fi ]nt`rziate f[r[ a modifica termenul final de realizare al
proiectului. Graficele Gant nu pot fi folosite pentru astfel de analize, ]n acest caz fiind
recomandat[ metoda de reprezentare a proiectului printr-un graf.

16.3. Reprezentarea proiectelor prin grafuri
Fiecare activitate este reprezentat[ ]n graf printr-un arc. }nceputul =i sf`r=itul fiec[rei
activit[i sunt indicate printr-un cerc numit nod. Fiec[rui nod i se atribuie un num[r. Modul
de atribuire a numerelor este arbitrar. Pe m[sur[ ce se construie=te graful nodurile se pot
renumerota, dar trebuie p[strate corect relaiile de preceden[ ]ntre activit[i. Fiecare
activitate trebuie s[ ]nceap[ ]n nodul ]n care activitatea precedent[ se termin[. De exemplu, ]n
figura 16.2, activitatea C ]ncepe ]n nodul 3, deoarece activitatea precedent[ B se termin[ aici.
2

A
1

4
B

C

3

Figura 16.1 – Graful pentru activit[ile de la A la C

A

2

4
D

1

5
E

C
B

3
Figura 16.2 – Graful parial

Complicaii apar ]n momentul ]n care ]ncerc[m s[ ad[ug[m activitatea D ]n graf. +i A
=i C sunt activit[i precedente pentru D, =i cum vrem ca ]n graf activitatea D s[ apar[ o
singur[ dat[ trebuie s[ combin[m nodurile 2 =i 4 din figura 16.2 ]ntr-unul singur. Acest lucru
este ar[tat ]n figura 16.3. Nodul 2 (au fost renumerotate nodurile) reprezint[ evenimentul ]n
care activit[ile A =i C au fost terminate. Activitatea E, care are ca activitate precedent[ doar
pe D poate fi ad[ugat[ f[r[ dificultate. C`nd ]ncerc[m s[ ad[ug[m activitatea F apar din nou
probleme. Cum F are activitate precedent[ pe C, ar trebui ca activitatea F s[ ]nceap[ ]n nodul
3. Dar acest lucru ar ]nsemna c[ activitatea F are ca activitate precedent[ =i pe A, ceea ce este
incorect.

Aceast[ dilem[ poate fi rezolvat[ prin introducerea unei activit[i fictive, reprezent[
prin linie punctat[ ]n figura 16.4. Aceast[ activitate nu necesit[ nici timp =i nici resurse.
2

5

D

A
1

4
B

6

F

C

7

E

Figura 16.4 – Introducerea unei activit[i fictive

3

Astfel, figura 16.4 arat[ c[ activitatea D poate ]ncepe dup[ ce =i A =i C s-au terminat.
Similar, F poate ]ncepe dup[ ce activitatea C s-a terminat.
Putem generaliza modul ]n care introducem o activitate fictiv[ ]n modul urm[tor:
Presupunem c[ vrem s[ ad[ug[m o activitate A, ]n nodul de start N, dar nu toate activit[ile
care se termin[ ]n nodul N sunt activit[i precedente ale acestei activit[i. Pentru aceasta se
creeaz[ un nou nod M, cu o activitate fictiv[ de la nodul M la nodul N. Toate activit[ile care
se termin[ ]n N =i sunt predecesoare ale activit[ii A se vor termina ]n nodul M. Acum
activitatea A poate ]ncepe ]n nodul M.
Figura 16.5 prezint[ graful asociat tabelului 16.1.
2

5

D

A

E

1

4
B

6

F

C

H
7

G

3

J

I

8

Figura 16.5 – Graful de reea
Fiecare activitate este identificat[ printr-un nod de start =i unul de terminare. }n graful
din figura 16.5 s-ar putea face confuzia c[ G =i H reprezint[ aceea=i activitate. Pentru a evita
confuzia se introduce o nou[ activitate fictiv[ (figura 16.6).
H

6

7
G
8
Figura 16.6 – Introducerea celei de a doua activit[i fictive
Astfel, graful final are forma din figura 16.7.


A(3)

2

5

D(4)

E(8)

1

4

B(5)

F(2)

C(3)

6

H(2)

7

G(4)

3

8

J(3)

I(5)
9
Figura 16.7 – Graful final
Din tabelul 4.1. se poate calcula (adun`nd duratele de realizare ale activit[ilor) c[
timpul total de realizare al proiectului este de 39 de s[pt[m`ni. Termenul acesta poate fi mai
mic deoarece unele activit[i se pot desf[=ura simultan (de exemplu activit[ile A =i B).
Pentru a afla termenul minim de realizare al proiectului trebuie s[ calcul[m drumul
critic. Un drum ]ntr-un graf este o succesiune de activit[i de la nodul iniial (1) la nodul final
(9). De exemplu secvena B-I necesit[ 10 s[pt[m`ni pentru a fi realizat[, secvena B-C-D-E-J
23 de s[pt[m`ni. }ntr-un graf pot fi identificate mai multe drumuri de la nodul iniial la cel
final, cu durate diferite. Se pune problema determin[rii celui mai lung drum de la nodul
iniial la cel final. Acest drum, numit drum critic, va determina timpul de realizare al
proiectului, deoarece nici un alt drum nu este mai lung. Dac[ activit[ile de pe drumul critic
sunt ]nt`rziate, ]ntregul proiect va fi ]nt`rziat. Din aceast[ cauz[ activit[ile care se g[sesc pe
drumul critic se numesc activit[i critice. Activit[ile critice trebuie realizate „la termen“.
Problema se rezolv[ ]n modul urm[tor:
1. Se calculeaz[ pentru fiecare activitate cel mai devreme termen de ]ncepere =i cel
mai devreme termen de terminare.
Vom nota cu:
DI – cel mai devreme termen pentru ]nceperea unei activit[i
DT – cel mai devreme termen pentru terminarea unei activit[i
t – durata estimat[ a activit[ii.
Pentru o activitate, relaia dintre aceste m[rimi este: DTˆDI‡t
Termenul DI pentru o activitate care pleac[ dintr-un nod este cel mai mare DT al
activit[ilor care se termin[ ]n acel nod.
Pentru fiecare activitate din reea se calculeaz[ DI =i DT. Rezultatul este prezentat
]n figura 16.8.
A(0,3)

2

5

D(8,12

E(12,20)

1

4

B(0,5)

C(5,8)
3

F(8,10)

6

Figura 16.8 –
Termenele DI =i DT

H(10,12)
7

G(10,14)
8

J(20,23)

I(5,10)
9

Deci, cel mai devreme termen de terminare al proiectului este de 23 de s[pt[m`ni.
2. Se calculeaz[ cel mai t`rziu termen de ]ncepere =i terminare a activit[ii. Pentru a
identifica activit[ile critice =i intervalele de timp cu care activit[ile necritice pot fi
]nt`rziate f[r[ a afecta termenul de finalizare al proiectului, se parcurge graful
]napoi de la nodul final la nodul iniial. Ideea este c[ odat[ ce se cunoa=te termenul
de realizare al proiectului (23 de s[pt[m`ni), pornind de la aceast[ valoare putem
calcula cel mai t`rziu termen la care se poate termina o activitate f[r[ a ]nt`rzia
]ntregul proiect. Evaluarea ]ncepe de la nodul final spre nodul iniial.
Vom nota cu:
TI – cel mai t`rziu termen de ]ncepere a unei activit[i
TT – cel mai t`rziu termen de terminare a unei activit[i
Relaia dintre aceste m[rimi este: TI ˆ TT – t
Termenul TT pentru o activitate care se termin[ ]ntr-un nod este cel mai mic TI al
activit[ilor care pleac[ din acel nod.
Rezultatele sunt prezentate ]n figura 16.9.
A(5,8)

2

5

D(8,12)

E(12,20)

1

4

B(0,5)

C(5,8)
3

F(14,16)

6

H(18,20)
7

G(16,20)
8

J(20,23)

I(18,23)
9
Figura 16.9 – Calcularea TI =i TT
3. Determinarea rezervei de timp asociate fiec[rei activit[i.
Rezerva de timp este timpul cu care o activitate poate fi ]nt`rziat[ f[r[ a afecta
termenul de finalizare al proiectului. Rezerva de timp (RT) se calculeaz[ cu
formula: RT ˆ TI - DI ˆ TT – DT
De exemplu, pentru activitatea G, rezerva de timp este:
RTG ˆ TIG – DIG ˆ 16 - 10 ˆ 6 sau
RTG ˆ TTG – DTG ˆ 20 - 14 ˆ 6
Aceasta ]nseamn[ c[ activitatea G poate ]nt`rzia cu 6 s[pt[m`ni dup[ cel mai
devreme termen de ]ncepere a activit[ii f[r[ a ]nt`rzia proiectul.
Pentru activitatea C:
RTC ˆ TIC – DIC ˆ5 - 5 ˆ 0
Deci activitatea C nu are rezerv[ de timp =i trebuie s[ ]nceap[ ]n s[pt[m`na 5. Cum
aceast[ activitate nu poate fi ]nt`rziat[ f[r[ a afecta ]ntregul proiect, ]nseamn[ c[
aceast[ activitate este o activitate critic[.
Activitatile care au rezerva de timp 0 sunt activitati critice.


16.4. Rezolvarea cu Excel
Rezolvarea problemelor de managementul proiectelor cu Excel se face folosind
abordarea bazat[ pe grafuri. Foaia de calcul care conine acest model este prezentat[ ]n figura
16.10.
Datele =i formulele introduse sunt cele rezultate prin dezvoltarea grafului ata=at
proiectului. De exemplu, deoarece cel mai t`rziu termen de terminare a activit[ii F este cea
mai mic[ valoare dintre cele mai t`rzii termene de ]ncepere ale activit[ilor G, F =i K, formula
din celula G7 va fi ˆ MIN(F8, F9, F12). Deoarece cel mai devreme termen pentru ]nceperea
activit[ii D este cea mai mare valoare din cele mai devreme termene de terminare ale
activit[ilor A =i C, formula din D5 este ˆ MAX(E2,E4). }n coloana activitate critic[ este
trecut cuv`ntul DA pentru activit[ile care au abaterea 0.
1
2
3
4
5
6
7
8
9
10
11
12
13

A
ACTIVITATE
A
B
C
D
E
F
G
H
I
J

B
DESCRIERE
Selectarea birourilor
Stabilirea planului de organizare si a celui financiar
Determinarea personalului necesar
Proiectarea interioarelor
Amenajarea birourilor
Selectarea personaluli care se va muta
Angajarea de personal nou
Mutarea propriu-zisa
Stabilirea relatiilor cu noii partener din Brasov
Instruirea personalului

C
DURATA
3
5
3
4
8
2
4
2
5
3

D
DI
0
0
5
8
12
8
10
10
5
20

LUNGIMEA MAXIMA A PROIECTULUI

E
DT
3
5
8
12
20
10
14
12
10
23

F
TI
5
0
5
8
12
14
16
18
18
20

G
TT
8
5
8
12
20
16
20
20
23
23

H
ABATERE
5
0
0
0
0
6
6
8
13
0

23

Figura 16.10 – Foaia de calcul Excel
Formulele utilizate ]n foaia de calcul sunt:
Celula
D4
D5
D6
D7
D8
D9
D10
D11
E2
F2
G2
G3
G4
G5
G6
G7
G8
G9
G10
G11
H2
I2

Formula
ˆMAX(E3)
ˆMAX(E2,E4)
ˆMAX(E5)
ˆMAX(E4)
ˆMAX(E7)
ˆMAX(E7)
ˆMAX(E3)
ˆMAX(E6,E8,E9)
ˆD2‡C2
ˆG2-C2
ˆMIN(F5)
ˆMIN(F4,F10)
ˆMIN(F5,F7)
ˆMIN(F6)
ˆMIN(F11)
ˆMIN(F8,F9)
ˆMIN(F11)
ˆMIN(F11)
Ê13
Ê13
ˆF2-D2
ÎF(H2ˆ0,“DA“,“NU“)

Se copieaz[ ]n
E3:E11
F3:F11
H3:H11
I3:I1

I
CRITICA?
NU
DA
DA
DA
DA
NU
NU
NU
NU
DA

E13

ˆMAX(E2:E11)

-

16.5. Reprezentarea grafică a graficelor Gant în Excel
}n graficul Gant activit[ile sunt afi=ate pe axa vertical[, iar pe axa orizontal[ este
reprezentat timpul. Graficul indic[ cel mai devreme termen de ]ncepere a fiec[rei activit[i =i
durata activit[ii. Vom ilustra modul de construire a graficelor Gant pentru exemplul din
figura 16.10.
1. Se selecteaz[ datele care vor fi reprezentate ]n grafic: activit[ile (A1:A11), durata
activit[ilor (C1:C11) =i cel mai devreme termen de ]ncepere a activit[ilor
(D1:D11).
2. Se creeaz[ un grafic de tip Staked Bar.
3. Se selecteaz[ seria DI. Se apas[ butonul din dreapta al mouse-ului =i se selecteaz[
comanda Format Series. Se selecteaz[ butonul Series Order =i se stabile=te pentru
afi=area seriilor ordinea DI, Durata. Se selecteaz[ butonul Patterns, =i ]n seciunile
Border =i Area se selecteaz[ opiunile None. Deci barele ata=ate termenelor de
]ncepere ale activit[ilor vor fi transparente, iar barele care reprezint[ durata
activit[ilor vor ap[rea ]n prelungirea lor.
Se selecteaz[ seria Durata, se apas[ butonul din dreapta al mouse-ului =i se
selecteaz[ comanda Format Series. Se selecteaz[ butonul Data Labels, opiunea
Show Value. Astfel ]n dretul fiec[rei bare va fi afi=at[ durata activit[ii.
Se selecteaz[ axa Y, se apas[ butonul din dreapta al mouse-ului =i se selecteaz[
comanda Format Axis. Se selecteaz[ butonul Scale, opiunile Categories in
reverse order =i Value (Y) axis crosses at maximum category. Astfel activit[ile
vor fi afi=ate ]ncep`nd din partea de sus a axei y.

16.6. Modelul de analiză a drumului critic/cost
Pentru reducerea timpului de realizare a unui proiect, analistul poate ]ncerca reducerea
duratei ]n care se efectueaz[ anumite activit[i de pe drumul critic prin alocarea de resurse
suplimentare. De exemplu, o activitate care dureaz[ ]n mod normal 2 s[pt[m`ni dac[ se
lucreaz[ 8 ore pe zi, poate fi terminat[ mai repede dac[ se lucreaz[ peste program sau dac[ se
m[re=te num[rul de muncitori. Acest lucru, bine]neles, se realizeaz[ cu preul unor costuri
crescute. Problema care se pune este: „Ce activit[i ar trebui urgentate astfel ]nc`t reducerea
termenului final de realizare al proiectului s[ se fac[ cu costuri minime?“.
Acest model presupune c[ costul este o funcie liniar[ de timp, descresc[toare, deoarece
orice efort de urgentare este ]nsoit de cre=terea cheltuielilor (figura 16.11).
Cost
Cost
maxim
Cost
minim
Timp
minim

Timp
maxim

Figura 16.11 - Funcia cost - durat[

Timp


Pentru fiecare activitate se cunosc urm[toarele date:
Timpul normal – timpul maxim de realizare a activit[ii
Costul normal – costul necesar pentru realizarea activit[ii ]n timpul normal
de lucru
Timpul minim - timpul minim ]n care se poate realiza activitatea
Cost maxim
- costul necesar pentru realizarea lucr[rii ]n timpul minim
Pentru prezentarea metodei vom folosi urm[torul exemplu:
Un proiect, cu graful asociat prezentat ]n figura 16.13, este alc[tuit din 5 activit[i.
Pentru fiecare activitate se cunosc timpul normal, timpul minim, costul normal =i costul
maxim (prezentate ]n tabelul 16.2).

Activitate
A
B
C
D
E
Total

Timp normal
(ore)
32
40
50
24
120

Cost normal
($)
640
480
1000
288
4800
7208

Timp minim
(ore)
20
30
30
15
70

Cost maxim
($)
800
720
1200
360
5600

Costul
urgent[rii/or[
13.3
24
10
8
16

Tabelul 16.2 - Activit[ile proiectului
}n ultima coloan[ din tabel s-a calculat pentru fiecare activitate costul urgent[rii pe or[,
egal cu (Costul maxim-Costul normal)/(Timpul normal-Timpul minim) .
Figura 16.12 ilustreaz[ funcia cost - durat[ pentru activitatea A.
Cost
800
640
20

Timp

32

Figura 16.12 - Funcia cost - durat[ pentru activitatea A
Graful asociat problemei este prezentat ]n figura 16.13.
2

A
32

B
40

1

4

C

D

50
3

E
120

24

Figura 16.13 – Graful asociat problemei

5


Utiliz`nd duratele normale pentru fiecare activitate, cel mai devreme termen pentru
finalizarea proiectului este 194 ore (pe drumul critic C-D-E).
Pentru a reduce termenul de finalizare al proiectului la 193 de ore o activitate de pe
drumul critic trebuie urgentat[ cu o or[. Cum costul urgent[rii pe or[ pentru activitatea D este
mai mic dec`t costurile urgent[rii pe or[ pentru activit[ile C =i E (8‹10 =i 8‹16), se va
urgenta activitatea D cu o or[. Astfel, proiectul se va termina ]n 193 de ore, drumul critic va
fi C-D-E =i costul total 7208‡8ˆ7216.
Dac[ termenul de finalizare mai trebuie redus cu o ]nc[ or[, la 192 ore, aplic`nd un
raionament asem[n[tor se urgenteaz[ activitatea D cu ]nc[ o or[ =i costul marginal va cre=te
cu 8$.
Dac[ termenul de finalizare trebuie redus mai mult, la 191 ore, problema se complic[.
Situaia este ilustrat[ ]n figura 16.4. Acum exist[ dou[ drumuri critce A-B-E =i C-D-E,
ambele de 192 ore.
2

A

B

32

40

1

4
C

D

50

E

5

120

22

3

Figura 16.4 – Graful pentru timpul de finalizare de 191 ore
Urgentarea uneia dintre activit[ile A, B, C, D cu o or[ va reduce un drum cu o or[, dar
drumul critic va r[m`ne tot de 192 ore. Un drum critic de 191 de ore se poate obine dac[ se
urgenteaz[ activit[i de pe ambele drumuri, sau dac[ se urgenteaz[ doar activitatea E. Deci
exist[ mai multe alternative, iar dintre acestea trebuie g[sit[ soluia care are costul minim.
Pentru grafuri complexe rezolvarea ]n acest mod ar fi foarte greoaie. Problema poate fi
rezolvat[ simplu cu ajutorul program[rii liniare. Figura 16.5 conine modelul ata=at
problemei.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

A
Activitate
A
B
C
D
E

B
Timp normal
32
40
50
24
120

C
Cost normal
640
480
1000
288
4800

Activitate Durata urgentarii Durata activitatii
A
0
32
B
0
40
C
0
50
D
0
24
E
0
120
Termenul final:
Costul urgentarii =
0

D
E
F
G
Timp minim Cost maxim Durata urgentare Cost/ora de urgentare
20
800
12
13.33333333
30
720
10
24
30
1200
20
10
15
360
9
8
70
5600
50
16
DI
0
32
0
50
74

DT
32
72
50
74
194

TI
2
34
0
50
74

TT
34
74
50
74
194

H

I

Abatere
2
2
0
0
0

Activitate critica

194

Figura 16.5 – Foaia de calcul utilizat[ pentru rezolvarea problemei

***
***
***


Formulele utilizate ]n foaia de calcul sunt:
Celula
F2
G2
D9
D10
D11
D12
D13
E9
F9
G9
G10
G11
G1
G13
H9
I9
D14
C15

Formula
ˆB2-D2
ˆ(E2-C2)/(B2-D2)
0
Ê9
0
Ê11
ˆMAX(E10,E12)
ˆD9‡C9
ˆG9-C9
ˆF10
ˆF13
ˆF12
ˆF13
Ê13
ˆF9-D9
ÎF(H9ˆ0,“***“,““)
Ê13
ˆSUMPRODUCT(B9,B13,G2:G6)

Se copieaz[ ]n
F3:F6
G3:G6
E10:E13
F10:F13
H10:H13
I10:I13
-

}n prima parte a foii de calcul se introduc timpul normal, costul normal, timpul minim
=i costul maxim de realizare a fiec[rei ativit[i. Pe baza acestor date, se calculeaz[ ]n coloana
Durata maxim[ a urgent[rii durata maxim[ cu care poate fi urgentat[ fiecare activitate
(diferena dintre timpul normal =i timpul minim), iar ]n coloana urm[toare costul urgent[rii
pe or[ (diferena dintre costul maxim =i costul normal raportat[ la durata maxim[ a
urgent[rii).
Al doilea tabel din foaia de calcul conine variabilele de decizie ale problemei –
duratele cu care poate fi urgentat[ fiecare activitate (]n domeniul B9:B13). Iniial toate
valorile vor avea valoarea 0.
}n coloana Durata activit[ii se calculeaz[ durata activit[ii ]n cazul ]n care aceasta va fi
urgentat[ cu valoarea din coloana Durata urgent[rii (diferena dintre durata normal[ =i durata
urgent[rii).
}n coloanele urm[toare se calculeaz[ cele mai devreme =i cele mai t`rzii termene de
]ncepere =i terminare al fiec[rei activit[i, respect`nd succesiunea activit[ilor (la fel ca ]n
exemplul anterior). Apoi, se calculeaz[ pentru fiecare activitate abaterile =i se introduc
formulele pentru determinarea activit[ilor critice.
Funcia obiectiv (celula C15) este minimizarea costului total de urgentare, calculat ca
suma produselor dintre duratele cu care se urgenteaz[ fiecare activitate =i costul urgent[rii
activit[ii pe unitatea de timp - min(C15).
Restriciile problemei sunt:
1. Durata ]n care trebuie realizat proiectul (coninut[ ]n celula D14). De exemplu dac[
proiectul ar trebui terminat ]n 184 de ore, restricia ar fi D14ˆ184
2. Durata cu care poate fi urgentat[ fiecare activitate nu poate dep[=i durata maxim[
de urgentare, iar aceste durate sunt numere pozitive. Deci,
B9 : B13 ≥ 0 si
B9 : B13 ≤ F 2 : F 6

Se rezolv[ problema cu ajutorul Solver-ului, iar rezultatele obinute arat[ c[ pentru ca
proiectul s[ se termine cu costuri minime ]n 184 de ore, trebuie urgentate lucr[rile D cu 2 ore
=i E cu 8 ore. Costul suplimentar al urgent[rii ar fi ]n acest caz de 144$.

Rezolvarea problemelor de analiza decizionala

CAPITOLUL 17
REZOLVAREA PROBLEMELOR DE ANALIZĂ DECIZIONALĂ
17.1. Modele de analiză decizională
Principalele elemente ale unui proces decizional sunt:
1. Agentul decizional.
2. Tipul problemei decizionale. Dac[ parametrii problemei analizate sunt cunoscui se
spune c[ avem de a face cu decizii ]n condiii de certitudine. }n cazul unor
evenimente ale c[ror probabilit[i de apariie sunt cunoscute, se spune c[ procesul
decizional are loc ]n condiii de risc. Dac[ probabilit[ile de apariie ale
evenimentelor sunt aleatoare (nu sunt cunoscute), atunci decizia este adoptat[ ]n
condiii de incertitudine.
3. Variantele posibile de aciune, pe care decidenii le au la dispoziie.
4. Strategiile posibile de aciune ale managerilor. Aceste strategii constau ]n diverse
reguli care permit alegerea unei variante din cele existente.
5. Obiectivele procesului de decizie (scopul urm[rit de manageri). Aceste obiective se
concretizeaz[ fie ]n restricii, fie ]n funcii scop.
Evenimentele care pot ap[rea, dar pe care agentul decizional nu le poate controla sunt
numite st[ri ale naturii.
Modelele de analiz[ decizional[ vor fi prezentate pe urm[torul exemplu:
Firma PDC a cump[rat la Bu=teni un teren pentru a construi un complex de vile.
Preurile de construcie ale acestora variaz[ ]ntre 300000$ =i 1200000$, ]n funcie de num[rul
de camere. }n urma studiilor efectuate au fost realizate trei proiecte de dimensiuni diferite: 6
vile cu 10 camere, 12 vile cu 20 de camere =i 18 vile cu 30 de camere. Factorul cheie ]n
selectarea uneia din cele trei alternative este evaluarea corect[ de c[tre managementul firmei
a cererii viitoare. Cu toate c[ piaa poate fi influenat[ prin publicitate, preurile de cazare
relativ mari fac ca cererea s[ depind[ de o varietate de factori asupra c[rora managementul nu
are control.
Managementul firmei crede c[ exist[ dou[ posibilit[i:
• acceptarea proiectului de c[tre pia[, =i deci o cerere mare
• cerere redus[.
Deci, pentru exemplul analizat exist[ dou[ st[ri ale naturii:
S1 – cerere mare
S2 – cerere redus[
=i trei alternative:
d1 – proiectul de dimensiune mic[
d2 – proiectul de dimensiune medie
d3 – proiectul de dimensiune mare
Utiliz`nd cele mai bune informaii disponibile, agentul decizional trebuie s[ evalueze
pentru fiecare alternativ[ =i stare a naturii „c`=tigul“ ce va fi obinut. }n funcie de problema
analizat[, acest „c`=tig“ poate reprezenta un profit, un cost, un timp, o distan[, sau orice alt[
m[sur[ care s[ reflecte „ie=irile“ problemei studiate.
}n tabelul 17.1 sunt prezentate profiturile evaluate pentru problema analizat[ (]n
termeni de milioane de dolari).

Alternativ[
Proiect de dimensiune mic[ - d1
Proiect de dimensiune medie – d2
Proiect de dimensiune mare – d3

St[ri ale naturii
Cerere mare (S1)
Cerere redus[ (S2)
8
7
14
5
20
-9

Tabelul 17.1 – Profiturile obinute pentru fiecare alternativ[ =i stare a naturii
V31ˆ20 arat[ c[ se anticipeaz[ un profit de 20 de milioane dolari dac[ se va selecta
proiectul de dimensiune mare =i cererea va fi mare, V32ˆ -9 arat[ c[ dac[ se va selecta
proiectul de dimensiune mare =i cererea este redus[, se va obine o pierdere de 9 milioane de
dolari.

17.2. Decizii în condiţii de incertitudine
Problemele decizionale care conin incertitudini apar atunci c`nd nu se cunosc
probabilit[ile de apariie ale st[rilor naturii. Aceste probleme pot fi abordate din mai multe
puncte de vedere, =i ]n mod corespunz[tor exist[ mai multe criterii de decizie. Deoarece prin
aplicarea diverselor criterii se pot obine recomand[ri diferite este bine c[ agentul decizional
s[ ]neleag[ foarte bine toate criteriile existente =i s[-l selecteze pe acela care i se potrive=te
cel mai bine.
Criteriul optimist (criterium maxi-max)
Pentru fiecare alternativ[ se determin[ cel mai bun „c`=tig“. Decizia recomandat[ este
cea cu „c`=tigul“ cel mai bun. Pentru problemele de maximizare „c`=tigul“ cel mai bun
]nseamn[ cea mai mare valoare, pentru problemele de minimizare „c`=tigul“ cel mai bun
]nseamn[ cea mai mic[ valoare.
Criteriul pesimist (criteriul maxi-min)
Pentru fiecare alternativ[ se determin[ cel mai defavorabil „c`=tig“. Decizia
recomandat[ este cea cu cel mai bun „c`=tig“ defavorabil.
Criteriul regretelor (criteriul mini-max)
Alternativa se alege lu`nd ]n considerare diferena dintre rezultatul optim ce s-ar fi
putut obine ]ntr-o anumit[ stare =i valoarea celorlalte rezultate. Aceast[ diferen[ este numit[
regret.
Rij =| VJ* − Vij |
unde:
Rij – „regretul“ asociat alternativei di =i st[rii naturii Sj
V*j - „c`=tigul“ corespunz[tor celei mai bune decizii pentru starea naturii Sj. Pentru
probleme de maximizare V*j este cea mai mare valoare pentru starea naturii Sj,
pentru probleme de minimizare V*j este valoarea cea mai mic[.
Vij - „c`=tigul“ corespunz[tor alternativei di =i st[rii naturii Sj.
Urm[torul pas este determinarea regretului maxim pentru fiecare alternativ[. }n final va
fi selectat[ alternativa cu cel mai mic „regret“ maxim.


17.3. Rezolvarea problemelor de analiză decizională în condiţii de
incertitudine în Excel
Criteriul optimist
}n figura 17.1 este prezentat[ foaia de calcul pentru rezolvarea problemei cu criteriul
optimist. Domeniul A4:C8 conine datele problemei. }n domeniul D6:D8 se calculeaz[
„c`=tigul“ maxim pentru fiecare alternativ[. }n celula D10 se calculeaz[ cel mai mare dintre
„c`=tigurile“ maxime ale fiec[rei alternative. }n domeniul E6:E8 se afi=eaz[ numele
alternativei recomandate.
Formulele utilizate sunt:
Celula
Formula
Se copieaz[ ]n:
D6
ˆMAX(B6:C6)
D7:D8
D10
ˆMAX(D6:D8)
E6
ˆIF(D6ˆ$D$10,A6,““)
E7:E8
A
1

B

C

D

E

Castig
maxim
8
14
20

Decizie
recomandata

Criteriul optimist

2
3
4

Alternativa
6 Proiect de dimensiune mica
7 Proiect de dimensiune medie
8 Proiect de dimensiune mare
5

Starea naturii
Cerere mare
Cerere redusa
8
7
14
5
20
-9

Proiect de dimensiune mare

9
10

20

Cel mai bun castig

Figura 17.1 – Criteriul optimist
Criteriul pesimist
pesimist. Singura diferen[ dintre foile de calcul din figura 17.1 =i 17.2 este c[ la criteriul
pesimist se determin[ „c`=tigul“ minim pentru fiecare alternativ[. Astfel, celula D6 conine
formula ˆMIN(B6:C6), care este copiat[ ]n celulele D7 =i D8.
A
1

B

C

D

E

Castig
maxim
7
5
-9

Decizie
recomandata
Proiect de dimensiune mica

Criteriul pesimist

2
3
4

Alternativa
5
6

Starea naturii
Cerere mare
Cerere redusa
8
7
14
5
20
-9

9
10

7

Cel mai bun castig

Figura 17.2 – Criteriul pesimist

Criteriul regretelor
regretelor.
Domeniul A4:C8 conine datele problemei.
Aceast[ problem[ presupune determinarea regretelor asociate fiec[rei alternative =i
fiec[rei st[ri a naturii. Formulele utilizate sunt:
Celula B14

- Se calculeaz[ „regretul“ fa[ de cea mai bun[ valoare a st[rii naturii
cerere mare. Formula utilizat[ este:
ˆMAX($B$6:$B$8)-B6
Se copieaz[ B14 ]n B15 =i B16
- Se calculeaz[ „regretul“ fa[ de cea mai bun[ valoare a st[rii naturii
cerere redus[. Formula utilizat[ este:
ˆMAX($C$6:$C$8)-C6
Se copieaz[ C14 ]n C15 =i C16
- Se calculeaz[ „regretul“ maxim. Formula utilizat[ este:
ˆMAX(B14:C14)
Se copieaz[ D14 ]n D15 =i D16
- Se calculeaz[ minimul „regretelor maxime“. Formula utilizat[ este:
ˆMIN(D14:D16)
- }n domeniul E14:E16 se afi=eaz[ numele alternativei recomandate. }n
celula E14 se introduce formula:
ˆIF(D14ˆ$D$18,A14,““).
Se copieaz[ E14 ]n E15:E16.

Celula C14

Celula D14
Celula D18
Celula E14

A
1

B

C

D

E

Regret
maxim
12
6
16

Decizie
recomandata

Criteriul regretelor

2
3
4

Alternativa
5

Starea naturii
Cerere mare
Cerere redusa
8
7
14
5
20
-9

9
10
11

Matricea regretelor

12

Alternativa
13

Starea naturii
Cerere mare
Cerere redusa
12
0
6
2
0
16

17
18

Regretul minimax

6

Figura 17.3 – Criteriul regretelor

Proiect de dimensiune medie


17.4. Decizii în condiţii de risc
}n multe probleme decizionale se poate estima probabilitatea cu care apar st[rile naturii.
Principala caracteristic[ a deciziilor ]n condiii de risc este c[ agentul decizional trebuie s[
aleag[ o alternativ[ pe baza probabilit[ilor de apariie a st[rilor naturii.
Not[m cu :
N - num[rul st[rilor naturii
P(Sj) – probabilitatea de apariie a st[rii SJ
La un moment dat poate ap[rea doar o stare a naturii, deci probabilit[ile trebuie s[
]ndeplineasc[ condiiile:
P ( S j ) ≥ 0 , pentru toate starile naturii
N

∑

j =1

P ( S j ) = P ( S 1 ) + ........ + P ( S N ) = 1

Valoarea a=teptat[ VA a unei alternative di este definit[ ]n moul urm[tor:
N

VA(di ) = ∑ P( S j )Vij
j =1

Altfel spus, „valoarea a=teptat[“ a unei alternative este suma ponderat[ a „c`=tigurilor“
alternativei analizate. Ponderea unui „c`=tig“ este probabilitatea asociat[ st[rii naturii j.
Pentru exemplul analizat, dac[ probabilit[ile de apariie ale st[rilor naturii sunt 0.8
pentr S1 =i 0.2 pentru S2, avem:
VA(d1)ˆ0.8*8‡0.2*7ˆ7.8
VA(d2)ˆ0.8*14‡0.2*5ˆ12.2
VA(d3)ˆ0.8*20‡0.2*(-9)ˆ14.2
}n final va fi selectat[ alternativa cu „valoarea a=teptat[“ cea mai bun[ (cea mai mare
valoare pentru criterii de maximizare, cea mai mica valoare pentru criterii de minimizare). }n
exemplul analizat se ]ncearc[ maximizarea profitului, deci cea mai bun[ alternativ[ este d3
(cu VAˆ14.2)

17.5. Rezolvarea problemei utilizând Excel
}n figura 17.4 este prezentat[ foaia de calcul folosit[ pentru luarea deciziilor ]n condiii
de risc.
A
1

B

C

D

E

Valoare
asteptata
7.8
12.2
14.2

Decizie
recom
andata

Decizii in conditii de risc

2
3
4
5
6
7
8
9

Alternativa
Proiect de dimensiune medie
Probabilitatea

Starea naturii
Cerere mare
Cerere redusa
8
7
14
5
20
-9
0.8
0.2


10
11

Valoarea asteptata m a
axim

14.2

Figura 17.4 – Luarea deciziei ]n condiii de risc

Domeniul A4:C9 conine datele problemei. Probabilit[ile de apariie ale celor dou[
st[ri ale naturii sunt introduse ]n celulele B9 =i C9.
}n domeniul D6:D8 se calculeaz[ „valoarea a=teptat[“ pentru fiecare alternativ[, iar ]n
domeniul E6:E8 se afi=eaz[ numele alternativei recomandate.
Formulele utilizate sunt:
Celula D6

Celula D11
Celula E6

- Se calculeaz[ „valoarea a=teptat[“ a alternativei d1. Formula utilizat[
este:
ˆSUMPRODUCT($B$9:$C$9,B6:C6)
Se copieaz[ D6 ]n D7 =i D8.
- Se calculeaz[ „valoarea a=teptat[“ maxim[. Formula utilizat[ este:
ˆMAX(D6:D8)
- Se determin[ alternativa recomandat[. Formula utilizat[ este:
ˆIF(D6ˆ$D$11,A6,““)
Se copieaz[ E6 ]n E7:E8

Pentru o problem[ de minimizare singura modificare ]n foaia de calcul ar fi schimbarea
formulei din celula D11 ]n ˆMIN(D6:D8).

Introducerea şi editarea datelor

CAPITOLUL 2
INTRODUCEREA ŞI EDITAREA DATELOR
2.1. Introducerea şi editarea datelor
Pe m[sur[ ce datele sunt introduse de la tastatur[, ele apar ]n celula activ[, dar =i ]ntro zon[ de deasupra foii de calcul, numit[ bar[ de formule (Figura 2.1). Dac[ bara de
formule nu este afi=at[, din meniul View se selecteaz[ comanda Formula Bar.
Figura 2.1 – bara de formule

}n bara de formule apare o bar[ clipitoare care indic[ locul unde va ap[rea urm[torul
caracter tastat.
Introducerea datelor se termin[ fie ap[s`nd tasta <Enter>, fie activ[nd o alt[ celul[
(cu mouse-ul, cu s[gei, cu <Tab> etc.). Dac[ introducerea nu se termin[ corect urm[toarele
comenzi nu vor mai putea fi aplicate.

2.2. Introducerea textelor
Datele de tip text includ caractere alfabetice, numere =i simboluri. Pentru a introduce
text ]ntr-o celul[ se selecteaz[ celula, se scrie textul =i apoi se valideaz[ prin ap[sarea tastei
<Enter>. }ntr-o celul[ se pot introduce cel mult 255 caractere. Textul introdus este aliniat ]n
celul[ la st`nga.
Dac[ un num[r trebuie introdus ca text (de exemplu un cod po=tal) ]naintea datelor
trebuie introdus un apostrof.
Dac[ textul este prea lung =i nu ]ncape ]n celula activ[, partea ]n exces va fi afi=at[ ]n
celula adiacent[ dreapt[, dac[ aceasta este liber[; dac[ nu este liber[, va fi afi=at doar textul
care ]ncape ]n celula activ[. Pentru a putea afi=a textul ]n ]ntregime trebuie m[rit[
dimensiunea coloanei active.
Pentru a modifica dimensiunea unei coloane se poziioneaz[ cursorul mouse-ului pe
marginea din dreapta a etichetei coloanei. Forma cursorului se va modifica (
). Se trage de
acest cursor =i se elibereaz[ butonul mouse-ului c`nd se ajunge la dimensiunea dorit[. O alt[
metod[ este aplicarea unui dublu clic c`nd apare acest cursor; ]n acest mod coloana va avea
dimensiunea textului de lungime maxim[ din coloan[.

2.3. Introducerea numerelor
Numerele sunt valori care conin caracterele 1 2 3 5 6 7 8 9 0 - ‡ /. E e.
Pentru a introduce un num[r, se selecteaz[ celula dorit[, se scrie num[rul =i se apas[
<Enter>. Dac[ ]ntr-o celul[ se introduce un num[r prea lung, Excel ]ncearc[ s[-l afi=eze ]n
format exponenial (1.53 E‡08 ˆ 1.53 * 108). Dac[ num[rul nu poate fi afi=at nici ]n format
exponenial atunci ]n celul[ apare #######. }n acest caz pentru a putea vizualiza num[rul se
va m[ri dimensiunea coloanei folosind metoda prezentat[ la introducerea textelor.
}n Excel exist[ mai multe formate numerice. C`teva din acestea sunt prezentate ]n
tabelul de mai jos:

Format
General
Number
Currency
Comma
Percent
Scientific (Exponential)
Fraction
Time/False

Afi=are
12345.6
12345.60
$1,234.78
12,345.6
123.454 %
1.23E‡04
12 3/4
True/False

Pentru introducerea unei fracii, trebuie scris num[rul ]ntreg, urmat de un spaiu =i
fracia respectiv[. Dac[ trebuie introdus[ numai partea fracionar[, se scrie zero, spaiu =i
fracia. Astfel, Excel poate interpreta datele introduse ca fiind ]n format dat[.
}ntr-o celul[ numerele sunt aliniate la dreapta.

2.4. Introducerea datelor şi orelor
Valorile de tip or[ pot fi introduse ]n urm[toarele formate:
Ora
15:31
15:31:45
8:31 PM
3.31:45 PM

Format
h:mm
h:mm:ss
h:mm:AM/PM
h:mm:ss AM/PM

La introducerea datelor trebuie s[ fim ateni ce sistem de introducere a datelor este
folosit pe calculatorul pe care ]l folosim. }n continuare vom folosi sistemul american de
introducere a datelor, marea majoritate a calculatoarelor fiind setate pe sistemul respectiv.
Valorile introduse corect vor apare ]n bara de formule ]n formatul lun[/zi/an, indiferent de
stilul de formatare a celulei.
Alte formate de introducere a datelor sunt:
Date
7/8/98
8-Jul-98
8 -Jul
Jul-98
7/8/98 09 09:45

Format
M/d/yy
d-mmm-yy
d-mmm (va fi folosit anul din data sistemului de calcul)
mmm-yy
M/d/yy h:mm

Excel ]nregistreaz[ datele =i orele sub form[ de numere. Fiec[rei date =i ore ]i este
ata=at un num[r. Aceste numere se numesc numere seriale. Numai formatul de afi=are este de
tip dat[ sau or[. Folosind aceast[ codificare, o dat[ reprezint[ num[rul de zile care despart
data de 1.01.1900 de data specificat[; ora reprezint[ o fraciune zecimal[ din 24 de ore.
Numerele seriale au proprietatea c[ permit calcularea zilelor scurse ]ntre dou[ date
specificate sau a duratelor dintre dou[ momente de timp. Numerele seriale ata=ate datelor
sunt numere ]ntregi, cele ata=ate orelor sunt numere subunitare.
Exemple:

Data
1-01-1900
2-01-1900
1-08-1998

Num[r serial
1
2
36008

Ora
0:0:0
12:00:00
23:59:59

Num[r serial
0
0.5
0.99

Implicit datele =i orele se aliniaz[ ]n celule la dreapta. Dac[ o dat[ nu este introdus[
corect ea este transformat[ ]n text =i informaia din celul[ va fi aliniat[ la st`nga. Acest mod
reprezint[ o metod[ foarte simpl[ de a verifica dac[ datele sau orele au fost introduse corect.
}n unele cazuri, de=i a fost utilizat un format corect pentru valori de tip dat[ sau or[,
rezultatul afi=at apare sub form[ de num[r. Acest lucru se ]nt`mpl[ c`nd celula respectiv[ a
fost formatat[ anterior cu un format altul dec`t General. }n acest caz celulei respective
trebuie s[ i se aplice formatul dat[ sau or[ corespunz[tor (vezi lecia 3).

2.5. Efectuarea modificărilor
Dac[ datele dintr-o celul[ au fost introduse gre=it acestea se pot corecta ]n modul
urm[tor:
1. Se activeaz[ celula care conine datele care trebuie modificate.
2. Se apas[ tasta <F2> sau se aplic[ un clic ]n linia de formule ]n dreptul locului unde
trebuie f[cute modific[ri.
3. Se fac operaiile de =tergere =i inserare necesare. Pentru a muta punctul de inserie se
folosesc tastele s[gei. Pentru =tergere se pot folosi tastele <Backspace> - pentru a
=terge un caracter la st`nga - =i <Delete> - pentru a =terge un caracter la dreapta.
4. Se apas[ tasta <Enter>.

2.6. Selectarea, copierea şi mutarea celulelor
C`nd o celul[ este activ[, cursorul mouse-ului poate lua trei forme:
Acest[ form[ de cursor apare dac[ cursorul mouse-ului este poziionat ]n
interiorul celulei. Cu acest cursor se realizeaz[ operaia de selecie a
celulelor
Acest[ form[ de cursor apare dac[ cursorul mouse-ului este poziionat pe
conturul celulei. Cu acest cursor se realizeaz[ operaia de mutare a
celulelor
Acest[ form[ de cursor apare dac[ cursorul mouse-ului este poziionat ]n
colul din dreapta-jos celulei. Cu acest cursor se realizeaz[ operaia de
copiere a celulelor

2.7. Selectarea celulelor
Celulele pot fi selectate ]n dou[ moduri: cu tastatura =i cu mouse-ul.
Selectarea celulelor cu tastatura
Pentru a selecta un domeniu de celule cu ajutorul tastaturii, se vor efectua urm[torii pa=i:
1. Se activeaz[ celula din colul din st`nga-sus al domeniului.

1. Celulele se selecteaz[ folosind combinaiile de taste: <Shift>+→, <Shift>+←,
→
←
<Shift>+→, <Shift>+↓. Celulele selectate apar ]n video-invers. Excepie face prima
→
↓
celul[ selectat[.
Selectarea celulelor cu mouse-ul
Pentru a selecta un domeniu de celule al[turate, se vor efectua urm[torii pa=i:
2. Se aplic[ un clic pe celula din colul din st`nga-sus al domeniului.
3. |in`nd butonul st`ng al mouse-ului ap[sat, se trage de mouse spre colul din dreapta-jos
al domeniului. Celulele selectate apar ]n video-invers. Excepie face prima celul[
selectat[.
4. Se elibereaz[ butonul mouse-ului.
Pentru a selecta celule care nu sunt al[turate se ine ap[sat[ tasta Ctrl ]n timp ce se aplic[ un
clic de mouse pe celulele individuale.
Pentru a selecta un r`nd ]ntreg sau o coloan[ de celule se aplic[ un clic pe eticheta de r`nd
sau de coloan[.

2.8. Copierea datelor
Prin copiere, datele originale r[m`n la locul lor, copia lor fiind plasat[ ]n locul indicat
de utilizator.
Pentru a realiza operaia de copiere, se vor efectua urm[torii pa=i:
1. Se selecteaz[ celula sau domeniul de celule care trebuie copiate.
2. Se aplic[ comanda Edit, Copy.
3. Se selecteaz[ prima celul[ din zona unde se va plasa copia.
4. Se aplic[ comanda Edit, Paste.
Pentru a copia date ]n celule al[turate, se poate utiliza =i o alt[ metod[, mai rapid[:
1. Se selecteaz[ celula care trebuie copiat[.
2. Se poziioneaz[ cursorul mouse-ului ]n colul din dreapta-jos al celulei.
3. C`nd cursorul mouse-ului ia forma unei cruci subiri, se apas[ butonul st`ng al mouseului =i se trage de mouse peste celulele ]n care se vor copia datele.

2.9. Mutarea datelor
Prin mutare datele sunt luate din poziia iniial[ =i sunt plasate ]n noua locaie.
Pentru a realiza operaia de mutare, se vor efectua urm[torii pa=i:
1. Se selecteaz[ celula sau domeniul de celule care trebuie mutate.
2. Se aplic[ comanda Edit, Cut.
3. Se selecteaz[ prima celul[ din zona unde se va plasa copia.
4. Se aplic[ comanda Edit, Paste.
O alt[ metod[, mai rapid[, este urm[toarea:
1. Se selecteaz[ celula care trebuie mutat[.
2. Se poziioneaz[ cursorul mouse-ului pe conturul celulei.
3. C`nd cursorul mouse-ului ia forma unei s[gei, se apas[ butonul st`ng al mouse-ului =i se
trage de mouse ]n noua poziie a datelor.

Formatarea foilor de calcul

CAPITOLUL 3
FORMATAREA FOILOR DE CALCUL
3.1. Formatarea foilor de calcul
Aspectul informaiilor din celulele unei foi de calcul poate fi modificat prin utilizarea
comenzii Format, Cells. La lansarea acestei comenzi pe ecran apare caseta de dialog Format
Cells (figura 3.1).

Figura 3.1 – caseta de dialog Format Cells
Coninutul casetei variaz[ ]n funcie de butonul selectat ]n partea superioar[ a
ferestrei. Opiunile posibile sunt:
• Number – pentru modificarea formatului numerelor
• Alignment – pentru modificarea tipului de aliniere din celul[
• Font – pentru modificarea fonturilor
• Borders – pentru ad[ugarea de chenare ]n jurul celulelor
• Patterns – pentru stabilirea culorii de fond ]n celul[
• Protection – pentru protejarea informaiilor din celul[

3.2. Modificarea formatului numerelor
Excel ofer[ o palet[ larg[ de formate numerice, care sunt prezentate ]n tabelul
urm[tor:
Format numeric
General

Exemple
10.7

Descriere
Excel afi=eaz[ valoarea a=a cum este introdus[.

Format numeric
Number

Exemple
-10.7
3400.50
(-120.39)

Currency
(Valut[)

$3,400.50
($3,400.50)

Accounting
(Contabilitate)

$3,400.00
$978.21

Date
(Dat[)

11/7

Time (Ora)

10:00

Percentage
(Procent)

99.50%

Fraction
(Fracie)
Scientific
(+tiinific)

½
3.40E 03

Text

135RV90

Special

02110

Custom
(Personalizat)

00.0%

Descriere
Formatul prestabilit Number are dou[ zecimale
Numerele negative apar scrise cu ro=u =i ]ntre
paranteze, precedate de semnul minus.
Formatul prestabilit Currency are dou[ zecimale =i
simbolul dolarului.Numerele negative apar scrise cu
ro=u =i ]ntre peranteze.
Acest format este folosit pentru a alinia simbolul
dolarului =i zecimalele ]n coloan[. Formatul
Accounting prestabilit conine dou[ zecimale =i
simbolul pentru dolar.
Formatul Date prestabilit cuprinde ora =i ziua
separate de o bar[ oblic[(/); se poate selecta ]ns[ =i
un alt format din cele disponibile.
Formatul Time prestabilit conine ora =i minutele
separate de dou[ puncte; se poate opta ]ns[ =i pentru
afi=area secundelor, sau a indicatorilor AM =i PM.
Formatul Percentage prestabilit cuprinde dou[
zecimale. Excel ]nmule=te valoarea din celul[ cu
100 =i afi=eaz[ rezultatul ]nsoit de simbolul pentru
procent
Formatul Fraction permite afi=area numerelor sub
form[ de fracie.
Formatul Scientific prestabilit cuprinde dou[
zecimale. Folosii acest format pentru afi=area
numerelor ]n format =tiinific.
Folosii formatul text pentru a afi=a at`t text c`t =i
numere, ]n aceea=I celul[. Excel va afi=a exact
exact ceea ce introducei dumneavoastr[.
Acest format este conceput special pentru afi=area
codurilor po=tale, a numerelor de telefon =i a
codurilor personale, astfel ]nc`t s[ nu fie necesar[
folosirea unor caractere speciale, cum ar fi liniuele
Formatul Custom este folosit pentru a crea propriul
format numeric. Se pot folosi codurile pentru
formatare din lista Type, care pot fi modificate.
Simbolul # reprezint[ un marcaj de rezervare pentru
un num[r, 0 reprezint[ un marcaj de rezervare
pentru zero, ? pentru ad[ugarea unui spaiu

Dup[ ce se stabile=te formatul numeric adecvat, se efectueaz[ pa=ii urm[tori:
1. Se selecteaz[ celula sau domeniul de celule ce conine valorile care trebuie formatate.
2. Se aplic[ comanda Format, Cells. Pe ecran va fi afi=at[ caseta de dialog Format Cells
figura 3.2).
3. Se aplic[ un clic pe butonul Number.
4. Din lista Category, se selecteaz[ formatul numerelor care va fi folosit.
5. }n partea dreapt[ a casetei se efectueaz[ modific[rile dorite pe formatul selectat. De
exemplu se poate stabili num[rul de zecimale cu care va fi afi=at num[rul (]n lista

Decimal places), sau modul ]n care vor fi afi=ate numerele negative (]n lista Negative

numbers).
6. Se aplic[ un clic pe butonul OK, sau se apas[ tasta Enter.
Excel va reformata celulele selectate conform opiunilor alese.
Figura 3.2 – caseta de dialog Format Cells - seciunea Number
Dac[ se introduce o dat[ calendaristic[ ]ntr-o celul[ formatat[ cu formatul Number,
data va ap[rea ca num[r (num[rul serial al datei). Pentru a rezolva problema, se modific[
formatul celulei din Number ]n Date.
Eliminarea formatului numeric dintr-o celul[ sau domeniu de celule se realizeaz[
aplic`nd formatul Genaral.

3.3. Utilizarea butoanelor pentru formatarea numerelor
Bara de instrumente de formatare conine mai multe butoane pentru stabilirea formatelor
numerice:
Buton

Denumire
Currency Style

Exemplu
$1200.90

Percent Style
Comma Style

20.90%
1,200.90

Increase Decimal

Adaug[ o zecimal[

Decrease Decimal

Elimin[ o zecimal[

Pentru a folosi unul dintre aceste butoane, se selecteaz[ celula sau domeniul care
trebuie formatate, apoi se aplic[ un clic pe butonul dorit

3.4. Modificarea tipului de aliniere din celule
La introducerea datelor ]ntr-o foaie de calcul din Excel, acestea sunt aliniate ]n mod
automat: textul este aliniat la st`nga, iar numerele la dreapta. At`t textul c`t =i numerele sunt
plasate iniial la baza celulelor. }n Excel se poate modifica alinierea datelor din celule at`t pe
vertical[ c`t =i pe orizontal[. Modul de aliniere a informaiilor se poate modifica din
seciunea Alignment a casetei de dialog Format Cell.
Pentru a schimba modul de aliniere a informaiilor, trebuie efectuai urm[torii pa=i:
1. Se selecteaz[ celula sau domeniul de celule care conine datele care trebuie aliniate
2. Se aplic[ comanda Format, Cells. Pe ecran va ap[rea caseta de dialog Format Cells.
3. Se aplic[ un clic pe butonul Alignment. Pe ecran vor ap[rea opiunile pentru aliniere
(figura 3.3):

Figura 3.3 – caseta de dialog Format Cells - seciunea Alignment
Elementele acestei casete sunt:
−
−

seciunea Text alignment care conine:
caseta Horizontal - ]n care se specific[ modul de aliniere pe orizontal[. Opiunile cele
mai folosite sunt:
• General – modul de aliniere implicit
• Left – aliniere la st`nga ]n celul[
• Center – centrare ]n celul[
• Right – aliniere la dreapta ]n celul[


•

Center Across Selection – centrare ]ntr-un domeniu de celule.
−
caseta Vertical - ]n care se specific[ modul de aliniere pe vertical[ ]n celul[. Opiunile
cele mai folosite sunt:
• Top – textul se aliniaz[ fa[ de marginea de sus a celulei.
• Bottom – textul este centrat pe verical[.
• Center - textul se aliniaz[ fa[ de marginea de jos a celulei.
−
seciunea Orientation. }n aceast[ seciune se specific[ unghiul sub care va fi afi=at
textul ]n celul[.
−
seciunea Text control. Aceast[ seciune conine trei opiuni:
• Wrap Text. }n mod normal Excel afi=eaz[ textul dintr-o celul[ pe un singur r`nd.
Cu opiunea Wrap Text, textul dintr-o celul[ poate fi afi=at pe mai multe r`nduri,
f[r[ a modifica l[imea celulei.
• Shrink to Fit. Aceat[ opiune adapteaz[ fontul textului la l[imea celulei curente.
Dac[ se modific[ l[imea celulei, m[rimea fontului cre=te sau se mic=oreaz[ ]n mod
corespunz[tor.
• Merge Cells. Cu aceat[ opiune se unesc mai multe celule.
4. Se aplic[ un clic pe butonul OK sau se apas[ tasta Enter.

3.5. Utilizarea butoanelor pentru aliniere
O metod[ rapid[ pentru alinierea informaiilor din celule presupune folosirea
butonelor de aliniere de pe bara cu instrumente de formatare. Aceste butoane sunt:
-

Aliniere la st`nga

-

Centrare

-

Aliniere la dreapta

-

Unire =i centrare

3.6. Modificarea fonturilor
C`nd se introduc date ]n Excel, acestea sunt formatate automat folosind fontul
implicit (de obicei Arial). Aspectul textului poate fi modificat folosind caseta de dialog
Format Cells.
Pentru a modifica fonturile ]n Excel, trebuie efectuai urm[torii pa=i:
1. Se selecteaz[ celula sau domeniul de celule ce conine datele care trebuie formatate.
2. Se aplic[ comanda Format, Cells.
3. Se selecteaz[ butonul Font din partea superioar[ a casetei. Pe ecran apare urm[toarea
caset[ de dialog (figura 3.4):
Elementele acestei casete sunt:
caseta Preview. }n aceast[ caset[ pot fi observate modific[rile care se fac ]n
celelalte c`mpuri ale casetei de dialog.
lista Font. Aceast[ list[ conine toate fonturile disponibile. De aici se selecteaz[
fontul dorit.

-

lista Font Style. Aceast[ list[ conine stilurile corpului de liter[ care pot fi aplicate
caracterelor: Bold, Italic, Regular, Bold Italic.
lista Size. }n aceast[ list[ se stabile=te ]n[limea ]n puncte a caracterelor.
lista Underline. Aceast[ list[ conine mai multe stiluri de subliniere. Lista conine
=i opiunea None, a c[rei selectare are ca efect anularea unei sublinieri.
lista Color. Din aceast[ list[ se selecteaz[ culoarea de scriere a literelor.
zona Effect. }n aceast[ zon[ pot fi specificate o serie de efecte speciale, prin
marcarea uneia sau mai multor opiuni propuse de Excel:
• Strikethrough - este trasat[ o linie la mijlocul literelor.
• Superscript - caracterele sunt scrise mai sus =i mai mici, ca un exponent.
• Subscript - caracterele sunt scrise mai jos =i mai mici, ca un indice..

Figura 3.4 – caseta de dialog Format Cells - seciunea Font
4. Se selecteaz[ opiunile dorite.

3.7. Modificarea fonturilor cu ajutorul butoanelor
O metod[ mai rapid[ de modificare a atributelor textului presupune folosirea butoanelor de
pe bara de instrumente de formatare:
Butonul Font:
La ap[sarea acestui buton apare lista fonturilor disponibile, din care se poate selecta fontul
dorit.
Butonul Size:
La ap[sarea acestui buton apare o list[ din care se stabile=te ]n[limea ]n puncte a
caracterelor.
Butonul Bold:

Dac[ acest buton este ap[sat are loc scrierea cu litere ]ngro=ate, dac[ nu textul este scris
normal.
Butonul Italic:
Dac[ acest buton este ap[sat are loc scrierea cu litere aplecate, dac[ nu textul este scris
normal.
Butonul Underline:
Dac[ acest buton este ap[sat are loc scrierea cu litere subliniate, altfel textul este scris
normal.
Folosind butoanele Bold, Italic =i Underline se pot aplica mai multe stiluri de scriere (orice
combinaie dintre ele). Activarea/ dezactivarea unui stil se face aplic`nd un clic pe butonul
respectiv.
Butonul Font Color:
La ap[sarea acestui buton apare o list[ din care se selecteaz[ culoarea de scriere a literelor.
Pentru a modifica atributele textului cu ajutorul butoanelor se vor efectua pa=ii urm[tori:
1. Se selecteaz[ celula sau domeniul ce conine textul al c[rui aspect trebuie modificat.
2. Se selecteaz[ butonul corespunz[tor.

3.8. Adaugarea de chenare la celule
}n mod normal liniile de reea din jurul celulelor nu sunt tip[rite. Excel ofer[
facilitatea de a ad[uga chenare celulelor selectate sau unui ]ntreg domeniu de celule.
Chenarul poate ap[rea pe cele patru laturi ale celulei sau numai pe laturile specificate.
Pentru a ad[uga chenare la o celul[ sau unui domeniu de celule, trebuie efectuai
urm[torii pa=i :
1. Se selecteaz[ celula (celulele) ]n jurul c[reia (c[rora) se va trasa chenarul.
2. Se aplic[ comanda Format, Cells. Pe ecran va ap[rea caseta de dialog Format Cells
(figura 3.5), din care se selecteaz[ butonul Borders.


Figura 3.5 – caseta de dialog Format Cells - seciunea Border
Elementele din aceast[ seciune sunt:
− lista Line. Din aceast[ list[ se selecteaz[ tipul liniilor cu care va fi trasat chenarul.
− lista Color. Din aceast[ list[ se selecteaz[ culoarea liniilor cu care va fi trasat
chenarul.
− zona Presets. }n aceast[ zon[ exist[ trei butoane:
• None. Dac[ ]n jurul unei celule sau a unui domeniu exist[ un chenar, acesta
este anulat cu opiunea None.
• Outline. }n cazul ]n care a fost selectat un domeniu de celule, liniile de reea
vor fi trasate doar ]n jurul zonei selectate. Nu sunt trasate liniile din interiorul
domeniului.
• Inside. Acest buton este activ doar dac[ este selectat un domeniu de celule.
Efectul obinut este trasarea liniilor de reea ]n interiorul zonei selectate.
− zona Border. }n aceast[ zon[ exist[ mai multe butoane, cu ajutorul c[rora se poate
modifica aspectul chenarului. Simbolul fiec[rui buton sugereaz[ linia din chenar
asupra c[reia se vor efectua modific[ri. Dac[ butonul este ap[sat linia va fi trasat[,
dac[ nu este ap[sat linia nu va fi trasat[. Pentru a modificarea culorii sau a tipului de
linie se selecteaz[ din listele Style =i Color aceste atribute, dup[ care se folose=te
butonul corespunz[tor din zona Border.

3.9. Adaugarea chenarelor cu ajutorul butoanelor
Pentru a ad[uga rapid chenare ]n jurul celulelor, se poate utiliza butonul Borders de pe bara de instrumente de formatare. La ap[sarea s[geii din dreptul acestui buton
apare o list[ din care se selecteaz[ tipul de chenar care trebuie aplicat. Dac[ se apas[ pe buton
(nu pe s[geat[) se va aplica ultimul tip de chenar selectat.

3.10. Stabilirea culorii de fundal din celule
Pentru a obine diverse efecte, ]n Excel se pot ad[uga culori de fundal celulelor din
foile de calcul.


Figura 3.6 – caseta de dialog Format Cells - seciunea Patterns
Pentru a aplica culori ]n fundalul celulelor, se vor efectua pa=ii urm[tori:
1. Se selecteaz[ celula sau domeniul de celule c[reia la care se va aplica o culoare de
fundal.
2. Se aplic[ comanda Format, Cells. Pe ecran va fi afi=at[ caseta de dialog Format Cells
(figura 2.6), din care se selecteaz[ butonul Patterns.
Elementele din aceast[ seciune sunt:
• lista Color. Din aceast[ list[ se selecteaz[ culoarea pentru fundal.
• lista Pattern. Din aceast[ list[ se selecteaz[ textura =i culoarea texturii care se aplic[
deasupra culorii de fudal.
• zona Sample. }n aceast[ zon[ se poate observa efectul opiunilor selectate.

3.11. Stabilirea culorii de fundal cu ajutorul butoanelor
Pentru a ad[uga rapid culoarea de fundal ]ntr-o celul[ sau domeniu, se poate utiliza
butonul Fill Color de pe bara de instrumente de formatare. La ap[sarea s[geii din
dreptul acestui buton apare o list[ din care se selecteaz[ culoarea de fundal care trebuie
aplicat[. Dac[ se apas[ pe buton (nu pe s[geat[) se va aplica ultima culoare selectat[.

Utilizarea formulelor în Excel

CAPITOLUL 4
UTILIZAREA FORMULELOR ÎN EXCEL
4.1. Utilizarea formulelor în Excel
Microsoft Excel a fost creat special pentru efectuarea de calcule numerice. Pentru a
indica programului modul de calcul trebuie scrise formule. Formulele sunt formate, de regul[,
din adrese de celule, valori =i operatori matematici. La efectuarea calculelor sunt respectate
toate regulile algebrice: prioritatea operaiilor de ]nmulire =i ]mp[rire, a parantezelor etc.
Toate formulele se introduc cu semnul = ]n fa[. Dac[ se omite semnul ˆ, Excel
consider[ c[ ]n celula respectiv[ a fost introdus un text.
}n continuare sunt prezentai principalii operatori utilizai ]n Excel.
Operatori aritmetici
Operator
–
+
*
/
%
^

Scop
sc[dere
adunare
]nmulire
]mp[rire
procente
ridicare la putere

Operatori de text
Folosind operatorii pentru text se pot concatena texte cuprinse ]ntre ghilimele (“”) sau
texte din celule diferite. De exemplu dac[ se scrie formula ˆ”Total v`nz[ri: ”$B4 rezultatul
este Total v`nz[ri: 28, dac[ celula B4 are valoarea 28.
Operatori pentru comparaii
Pentru a compara rezultatele se pot folosi operatorii pentru comparaii:
Operator

Scop

ˆ
<
>
<ˆ
>ˆ

egal cu
mai mic dec`t
mai mare dec`t
mai mic sau egal cu
mai mare sau egal cu

<>

diferit de

Pentru introducerea unei formule se execut[ pa=ii urm[tori:
1. Se selecteaz[ celula ]n care trebuie s[ apar[ rezultatul formulei;
2. Se scrie formula precedat[ de semnul =.
3. Se apas[ tasta <Enter>
Dup[ ap[sarea tastei <Enter> ]n celul[ apare automat rezultatul calculelor. Dac[
celula care conine formula este selectat[ din nou, se constat[:
• ]n bara de formule este afi=at[ formula de calcul;
• ]n celul[ apare rezultatul.
Exemplu:

Modelarea deciziilor utiliz`nd foile de calcul
O foaie de calcul conine urm[toarele valori:
• ]n celula A1 valoarea 7;
• ]n celula B1 valoarea 3.
Dac[ ]n celula C1 se scrie formula =A1+B1, dup[ ap[sarea tastei <Enter> ]n celul[ se va
afi=a rezultatul 10 (=7+3).
Excel poate fi setat astfel ]nc`t =i ]n celule s[ fie afi=ate formulele. Pentru aceasta
trebuie efectuai pa=ii urm[tori:
1.
Se aplic[ comanda Tools, Options.
2.
Se selecteaz[ butonul View (figura 4.1).

Figura 4.1 - caseta de dialog Options - seciunea View
3.
4.

}n zona Window Options se aplic[ un clic ]n c`mpul Formulas, pentru a-l marca.
Se selecteaz[ butonul OK.

Vizualizarea formulelor din celulele unei foi de calcul ar fi necesar[ doar ]n cazul ]n
care trebuie vizualizate toate formulele deodat[ (pentru tip[rire sau corecii).
Pentru revenirea la situaia ]n care ]n celule apar rezultatele formulelor se aplic[
procedura anterioar[, numai c[ se va demarca c`mpul Formulas.

4.2. Copierea formulelor
La copierea unei formule aceasta este adaptat[, pentru a corespunde poziiei celulei ]n
care va fi copiat[.
De exemplu, dac[ se copiaz[ formula =A1+B1 din celula C1 ]n celula D1, aceasta va
fi adaptat[ pentru coloana D, devenind =B1+C1. La copierea ]n celula C2, aceasta devine
=A2+B2.

Dac[ se copiaz[ o formul[ pe aceea=i linie, toi indicatorii de linie din celulele
formulei r[m`n neschimbai. Indicatorii de coloan[ se modific[. Peste o coloan[ la dreapta,
indicatorii de coloan[ se modific[ cu o liter[, peste dou[ coloane cu dou[ litere etc.
Dac[ se copiaz[ o formul[ pe aceea=i coloan[, prin copiere r[m`n neschimbai
indicatorii de coloan[. }n schimb se modific[ indicatorii de linie. Cu o linie mai jos indicatorii
de linie cresc cu 1, peste dou[ linii cu 2 etc.
Exemplu:
}n celula A5 se introduce formula =B2. Excel =tie c[ ]n celula A5 este folosit[ o celul[
care se g[se=te cu trei r`nduri mai sus =i o coloan[ la dreapta.
Prin copierea formulei din A5 ]n C8, Excel actualizeaz[ indicatorii de linie =i de
coloan[ astfel ]nc`t ]n celula C8 va fi referit[ o celul[ care se g[se=te tot cu trei r`nduri mai
sus =i o coloan[ la dreapta, dar fa[ de C8. Deci formula din aceast[ celul[ va fi =D5.
Pentru a copia o formul[ ]ntr-un domeniu de celule al[turat, se efectueaz[ urm[torii
pa=i:
1. Se aplic[ un clic pe celula care conine formula ce trebuie copiat[.
2. Se poziioneaz[ cursorul mouse-ului ]n colul din dreapta jos al celulei.
3. C`nd cursorul ]=i modific[ forma (apare un cursor de forma unei cruci mici) se
apas[ butonul st`ng al mouse-ului =i se trage de cursor peste celulele ]n care
trebuie copiat[ formula.
1.
2.
3.
4.

Formulele pot fi copiate =i ]n celule neadiacente, folosind comenzile Copy =i Paste:
Se aplic[ un clic pe celula care conine formula;
Se aplic[ comanda Edit, Copy;
Se aplic[ un clic pe celula ]n care se face copierea;
Se aplic[ comanda Edit, Paste.

4.3. Aplicaţie
Un fond mutual deine aciuni la mai multe societ[i comerciale. Pentru fiecare tip de
aciune se cunosc: valoarea de cump[rare, valoarea curent[ de pe pia[ =i num[rul de aciuni
cump[rate. S[ se calculeze profitul (sau pierderea) pentru fiecare tip de aciune.
Se va crea urm[toarea foaie de calcul (figura 4.2)

Figura 4.2
Foaia de calcul creat[ conine urm[toarele informaii:
• ]n coloana A – numele aciunilor;
• ]n coloana B – num[rul de aciuni cump[rate;
• ]n coloana C – valoarea la cump[rare a aciunilor;
• ]n coloana D – valoarea curent[ a aciunilor;
• ]n coloana E – se va calcula profitul sau pierderea pentru fiecare aciune.

}n celula E2 se va introduce formula =B2*(D2-C2).
Se copiaz[ formula din E2 ]n domeniul E3:E4, astfel:
1. Se aplic[ un clic ]n celula E2;
2. Se poziioneaz[ cursorul ]n colul din dreapta jos al celulei;
3. C`nd cursorul ]=i modific[ forma (apare un cursor de forma unei cruci mici ‡) se
apas[ butonul st`ng al mouse-ului =i se trage de cursor peste celulele E3 =i E4.

4.4. Utilizarea adreselor absolute
A=a cum am v[zut, la copierea unei formule Excel adapteaz[ indicatorii de linie =i de
coloan[ ai celulelor (referinele celulei) ]n funcie de noua poziie din foaia de calcul.
Modul de adresare al celulelor folosit p`n[ ]n prezent (notaia A7) folose=te sistemul
de adresare relativ.
Exist[ multe situaii ]n care, prin copierea unor formule, unele celule trebuie s[
r[m`n[ fixe (nu trebuie s[ se modifice indicatorii de linie/coloan[). }n acest caz se folose=te
sistemul de adresare absolut. }n faa indicatorilor care nu trebuie s[ se modifice se pune
simbolul $. De exemplu $A$7.
Exemplu:
}n celula A5 se introduce formula ˆ$B$2. Dup[ copierea formulei din A5 ]n C8, ]n
celula C8 formula va fi tot ˆ$B$2. Prin copiere nu s-a modificat nici indicatorul de linie, nici
cel de coloan[.
La copierea pe linie/coloan[ indicatorii de linie/coloan[ nu se modific[. }n aceste
cazuri formulele pot conine referiri mixte:
A$7 – linia este adresat[ absolut, coloana relativ.
$A7 - linia este adresat[ relativ, coloana absolut.

4.5. Aplicaţie
La firma XYZ preurile sunt stabilite ]n $. Datorit[ modific[rii cursului de schimb,
trebuie s[ recalculeze destul de frecvent preul ]n lei al produselor sale. S[ se proiecteze o
foaie de calcul astfel ]nc`t preul ]n lei s[ se calculeze automat la modificarea cursului de
schimb. Se va crea urm[toarea foaie de calcul (figura 4.3):

Figura 4.3
Dac[ ]n celula C4 s-ar introduce formula =B4*B1 (preul ]n lei * cursul de schimb) =i
acest[ formul[ s-ar copia ]n C5 =i C6, rezultatele nu ar fi corecte. }n C5 s-ar obine valoarea
0, iar ]n C6 #N/A.
Dac[ analiz[m formulele din aceste celule constat[m c[:
• celula C5 conine formula =B5*B2 (B4 s-a transformat ]n B5, iar B1 ]n B2);
• celula C6 conine formula =B6*B3 (B4 s-a transformat ]n B6, iar B1 ]n B3).

Formulele corecte din aceste celule ar trebui s[ fie =B5*B1, respectiv =B6*B1.
Deci celula B1 nu trebuie s[ se modifice atunci c`nd este copiat[. Pentru a realiza
acest lucru celula B1 trebuie referit[ absolut. Deci trebuie introdus simbolul $ ]n faa
indicatorului de linie. Formula corect[ care trebuie introdus[ ]n celula C4 este ˆB4*B$1. La
copierea acestei formule ]n C5 =i C6 se constat[ c[ formulele din aceste celule sunt corecte.
Celula C5 conine formula =B5*B$1, iar celula C6 conine formula =B6*B$1.


CAPITOLUL 5
INTRODUCEREA ŞI EDITAREA DATELOR
5.1. Utilizarea funcţiilor în Excel
Excel ofer[ peste 200 de funcii (formule predefinite), care permit crearea unor
formule complexe pentru o mare diversitate de aplicaii: =tiinifice, inginere=ti, de afaceri etc.
O funcie este definit[ de numele =i argumentele ei.
Argumentele unei funcii se introduc ]ntre paranteze. }n cazul ]n care se folosesc mai
multe argumente, acestea se separ[ prin virgul[. Funcia SUM, de exemplu, adun[ toate
numerele dintr-un domeniu de celule.
Adresa celulelor specificate formeaz[ argumentul funciei:
=SUM(A1:B2)
argumentul funciei
numele funciei
Dac[ o funcie nu are nici un argument, se scriu totu=i parantezele, numai c[ ]ntre ele
nu se va mai nota nimic. De asemenea, funciile pot conine at`t argumente obligatorii c`t =i
argumente opionale.
Cel mai folosit tip de argument este cel numeric, dar argumentele pot fi =i de tip text,
dat[, or[ sau matrice. Dac[ un text este folosit ca argument ]ntr-o funcie, el trebuie introdus
]ntre ghilimele.
Datorit[ num[rului mare de funcii ]ncorporate ]n Excel acestea au fost grupate ]n mai
multe categorii:
- Funcii matematice
- Funcii financiare
- Funcii logice
- Funcii de c[utare
- Funcii de lucru cu texte
- Funcii pentru lucrul cu date =i ore.
- Funcii statistice, etc.
etc.
Pentru a introduce o funcie ]n Excel se poate utiliza una din urm[toarele metode:
1. Funcia este scris[ de utilizator. }n acest caz se presupune c[ utilizatorul =tie
sintaxa funciei.


Figura 5. 1 – caseta de dialog Paste Function
2. Funcia este introdus[ folosind aplicaia Function Wizard, care se lanseaz[ la
aplicarea comenzii Insert, Function. Pe ecran va ap[rea caseta de dialog Paste
Function (figura 5.1).
}n lista Function Category sunt afi=ate categoriile de funcii ]ncorporate ]n Excel, iar
]n lista Function Name sunt trecute ]n ordine alfabetic[ funciile existente pentru categoria
selectat[.
Dup[ selectarea unei funcii, se aplic[ un clic pe butonul OK pentru a trece la
urm[toarea caset[ de dialog (figura 5.2).

Figura 5. 2
}n caseta de dialog a funciei alese (figura 5.2), trebuie introduse argumentele
necesare pentru funcia respectiv[. Casetele text pentru argumente trebuie s[ conin[ valori
sau referine de celule.
Funcia se termin[ de introdus select`nd butonul OK.
}n continuare vor fi prezentate funciile Excel ]nt`lnite mai frecvent, grupate pe
categorii.

5.2. Funcţii matematice
Funciile matematice constituie infrastructura oric[rei foi de calcul. Majoritatea
funciilor =tiinifice =i inginere=ti pot fi reg[site ]n grupele funciilor matematice.

ABS (num[r)
Funcia ABS returneaz[ valoarea absolut[ a unui num[r.
Exemple: ABS (–5) va returna valoarea 5
ABS (5) va returna valoarea 5
EXP (num[r)
Funcia EXP calculeaz[ exponeniala unui num[r (e ridicat la puterea specificat[ de
argumentul num[r).
Exemplu: EXP (0) va returna valoarea 1
LN (num[r)
Funcia LN calculeaz[ logaritmul natural al num[rului specificat.
Exemplu: LN (1) va returna valoarea 0
INT (num[r)
Funcia INT rotunje=te un num[r p`n[ la cea mai apropiat[ valoare ]ntreag[.
Exemple: INT (7.6) va returna valoarea 7
INT (–7.6) va returna valoarea 8
MOD (a, b)
Funcia MOD calculeaz[ restul (modulul) lui a ]mp[rit la b. Dac[ b este 0, se va afi=a
valoarea de eroare #DIV/0.
Exemplu: MOD (7, 6) va returna valoarea 1
MOD (32, 15) va returna valoarea 2
POWER (a, b)
Funcia POWER efectueaz[ ridicarea unui num[r a la puterea b.
Exemplu: POWER (2, 2) va returna valoarea 4
RAND ( )
Funcia RAND furnizeaz[ un num[r aleator ]ntre 0 =i 1. Funcia nu accept[
argumente. Ap[sarea tastei F9 va produce generarea altor numere.
ROUND (num[r, num[r de zecimale)
Funcia ROUND rotunje=te num[rul specificat ]n primul argument la num[rul de
zecimale specificat ]n al doilea argument.
Exemplu: ROUND (753.345, 2) va returna valoarea 753.35
ROUND (753.342, 2) va returna valoarea 753.34
ROUNDUP (num[r, num[r de zecimale)
Funcia ROUNDUP rotunje=te ]n sus num[rul specificat ]n primul argument, cu
num[rul de zecimale specificat ]n al doilea argument.
Exemplu: ROUNDUP (7.49, 1) va returna valoarea 7.5
ROUNDDOWN (num[r, num[r de zecimale)
Funcia ROUNDDOWN rotunje=te ]n jos num[rul specificat ]n primul argument, cu
num[rul de zecimale specificat ]n al doilea argument.
Exemplu: ROUNDDOWN (7.49, 1) va returna valoarea 7.4
SQRT (num[r)
Funcia SQRT extrage r[d[cina p[trat[ din argumentul specificat.

Exemplu: SQRT (4) va returna valoarea 2
SUM (num[r1, num[r2, …)
Funcia SUM calculeaz[ suma tuturor argumentelor. Argumentele pot fi valori, celule
individuale sau domenii de celule, dar num[rul lor este limitat la 30. Argumentele
numerice sunt ignorate.
Un domeniu de celule este specificat prin celula din colul st`ng sus al domeniului,
separatorul : =i celula din colul drept jos al domeniului.
Exemplu: SUM (A1:B3) va calcula suma valorilor din celulele A1, A2, A3,B1,B2, B3
AVERAGE (num[r1, num[r2, …)
Funciile AVERAGE calculeaz[ media aritmetic[ a tuturor argumentelor.
Argumentele pot fi valori, celule sau domenii de celule, dar num[rul lor este limitat la
30. Argumentele nenumerice sunt ignorate.
Exemplu: AVERAGE (A1:B3) va calcula media aritmetic[ a valorilor din celulele
A1, A2, A3, B1, B2, B3.
COUNT (num[r1, num[r2, …)
Funcia COUNT num[r[ ]n argumentele specificate celulele care conin numere.
Funcia poate avea ]ntre 1 =i 30 de argumente.
Exemplu: COUNT (A2:A5) va returna valoarea 3 atunci c`nd domeniul A2:A4
conine numerele 2,3,4, iar celula A5 este goal[.
MAX (num[r1, num[r2, …)
Funcia MAX returneaz[ valoarea celui mai mare argument. Funcia poate avea cel
mult 30 de argumente. Celulele goale, valorile de tip text, logic sau de tip eroare vor fi
ignorate.
Exemplu: MAX (A1:A3) va returna valoarea 10, dac[ numerele din acest domeniu
sunt: 1,10, 7, 4.
MIN (num[r1, num[r2, …)
Funcia MIN returneaz[ valoarea celui mai mic argument. Funcia poate avea cel mult
30 de argumente. Celulele goale, valorile de tip text, logic sau de tip eroare vor fi
ignorate.
Exemplu: MIN (A1:A3) va returna valoarea 1, dac[ numerele din acest domeniu sunt:
1,10, 7, 4.
IF (condiie, valoare adev[rat[, valoare fals[)
Funcia IF evalueaz[ o condiie. Dac[ condiia este adev[rat[, funcia va returna al
doilea aergument- valoarea adev[rat[. Dac[ condiia este fals[, funcia va returna al
treilea argument - valoarea fals[.
Exemplu: IF (A1<A2, “mai mic”, “mai mare”) va returna textul mai mic dac[ celula
A1 conine valoarea 7 =i celula A2 conine valoarea 10.

5.3. Funcţii logice
Funciile logice sunt folosite ]n cazurile ]n care trebuie evaluate mai multe condiii. }n
general, aceste funcii nu se folosesc singure, ele apar ca argumente la alte funcii (de
exemplu ]n funcia IF).


AND (condiia1, condiia2, …)
Funcia AND returneaz[ valoarea adev[rat[ (TRUE) dac[ toate condiiile specificate
]n argumente sunt adev[rate. Dac[ cel puin o condiie nu este adev[rat[, funcia
AND va returna valoarea fals (FALSE).
Funcia poate avea cel mult 30 de argumente.
OR (condiia1, condiia2, …)
Funcia OR returneaz[ valoarea adev[rat[ (TRUE) dac[ cel puin o condiie din cele
specificate ]n argumente este adev[rat[. Dac[ nici o condiie nu este adev[rat[,
funcia OR va returna valoarea fals (FALSE).
Funcia poate avea cel mult 30 de argumente.
NOT (condiie)
Funcia NOT returneaz[ valoarea adev[rat[ dac[ condiia este fals[ =i dac[ condiia
este adev[rat[.

5.4. Funcţii text
Funciile text permit manipularea informaiilor de tip text. Datele din foile de calcul
pot fi concatenate pentru a alc[tui titluri, propoziii, etichete.
CHAR (num[r)
Funciile CHAR returneaz[ caracterul care corespunde codului ASCII specificat ca
argument.
Exemplu: CHAR (65) va returna caracterul A.
CONCATENATE (text1, text2, …)
Funcia CONCATENATE efectueaz[ reuniunea tuturor argumentelor (cel mult 30).
Exemplu: CONCATENATE ("Microsoft", "Excel") va returna textul Microsoft
Excel.
EXACT (text1, text2)
Funcia EXACT compar[ textele text1 =i text2. Dac[ acestea sunt identice funcia va
returna valoarea adev[rat[ (TRUE), astfel se va reine valoarea logic[ FALSE.
Funcia face distincie ]ntre literele mici =i mari.
FIND (text-c[utat, surs[, start-num)
Funcia FIND caut[ primul argument, text-c[utat ]n textul din al doilea argument
surs[, ]ncep`nd cu poziia specificat[ de start-num. }n cazul ]n care acesta este g[sit,
funcia FIND returneaz[ poziia de ]nceput a textului c[utat. Dac[ argumentul startnum este ]n afara limitelor sau dac[ nu este g[sit[ o valoare, se va afi=a codul de
eroare #VALUE. Dac[ argumentul start-num nu este specificat, se presupune c[
acesta are valoarea 1.
Exemplu: FIND (B12, "ABCDE", 1) va returna valoarea 3 dac[ celula B12 conine
caracterul C.
LEFT (text, num-car)

Funcia afi=eaz[ primele num-car caractere din partea st`ng[ a unui text. Argumentul
num-car trebuie s[ fie mai mare ca 0. Dac[ se omite introducerea sa se va presupune
c[ este egal cu 1.
Exemplu: LEFT (A1, 5) va returna valoarea Micro dac[ ]n celula A1 se g[se=te textul
Microsoft.
RIGHT (text, num-car)
Funcia afi=eaz[ primele num-car caractere din partea dreapt[ a unui text. Argumentul
num-car trebuie s[ fie mai mare ca 0. Dac[ se omite introducerea sa se va presupune
c[ este egal cu 1.
Exemplu: RIGHT (A1, 4) va returna valoarea soft dac[ ]n celula A1 se g[se=te textul
Microsoft.
LEN (text)
Funcia LEN calculeaz[ num[rul de caractere din textul specificat de argument.
Exemplu: LEN ("Microsoft") va returna valoarea 9.
MID (text, start-num, num-car)
Funcia MID extrage un num[r de num-car caractere din text, ]ncep`nd cu poziia
start-num.
Exemplu: MID ("Microsoft Excel 7.0", 11, 5) va returna textul Excel.
LOWER (text)
Funcia LOWER converte=te eventualele majuscule din text ]n litere mici.
Exemplu: LOWER ("Microsoft Excel") va returna microsoft excel
PROPER (text)
Funcia PROPER determin[ afi=area textului cu litere mici, ]nceputurile de cuvinte
fiind scrise cu majuscule.
Exemplu: PROPER ("MICROSOFT EXCEL") va returna Microsoft Excel.
TRIM (text)
Funcia TRIM =terge toate blank-urile din text, astfel ]nc`t ]ntre cuvinte s[ r[m`n[ un
singur spaiu.
Exemplu: TRIM ("Microsoft Excel") va returna Microsoft Excel.
TEXT (valoare, format-text)
Funcia TEXT converte=te o valoare numeric[ ]n text =i o afi=eaz[ corespunz[tor
formatului indicat prin al doilea argument. Rezultatul apare afi=at ca un num[r
formatat, dar ]n realitate este de tip text. Se pot utiliza oricare din formatele numerice
predefinite sau personalizate, prezentate ]n lecia “Formatarea foilor de calcul”.
Exemplu: TEXT (457989, "$#, ##0.00") va returna $4,579.89

5.5. Funcţii pentru date şi ore
Programul Excel ata=eaz[ fiec[rei date calendaristice =i ore c`te un num[r serial.
Numerele seriale ata=ate datelor calendaristice sunt mai mari ca 1, cele ata=ate orelor sunt
subunitare. C`nd efectueaz[ calcule cu date =i ore, Excel folose=te aceste numere seriale,
numai formatul de afi=are este de tip dat[ sau or[.
Cele mai folosite funcii de lucru cu date =i ore sunt:


DATE (an, lun[, zi)
Funcia DATE returneaz[ num[rul serial pentru data specificat[.
Exemplu: DATE (1900, 1, 1) va returna 1 (num[rul serial al datei 1.1.1900)
NOW ( )
Funcia NOW calculeaz[ num[rul serial al datei =i al orei extrase din ceasul intern al
calculatorului. Excel actualizeaz[ data =i ora doar la deschiderea sau recalcularea foii.
Aceast[ funcie nu are argumente, ]ns[ este necesar[ introducerea parantezelor.
Exemplu: NOW ( ) va returna 9/ 10/ 99 10:43, dac[ aceasta este data curent[.
Dac[ rezultatul nu apare sub forma unei date, ]nseamn[ c[ este afi=at num[rul serial
ata=at. Pentru afi=area sub form[ de dat[ calendaristic[, celula respectiv[ trebuie
formatat[ de tip dat[ (vezi lecia Formatarea foilor de calcul).
YEAR (dat[ calendaristic[)
Funcia YEAR extrage anul din data specificat[.
Exemplu: YEAR ( 7/ 3/ 1999) va returna 1999.
MONTH (dat[ calendaristic[)
Funcia MONTH extrage luna din data specificat[.
Exemplu: MONTH ( 7/ 3/ 1999) va returna 7 (se consider[ c[ data este introdus[ ]n
formatul lun[/ zi/ an)
DAY (dat[ calendaristic[)
Funcia DAY extrage ziua din data specificat[.
Exemplu: DAY (7/ 3/ 1999) va returna 3.
TIME (or[, minut, secund[)
Funcia TIME calculeaz[ num[rul serial corespunz[tor num[rului de ore, minute =i
secunde indicate.
Exemplu: TIME (18, 4, 19) furnizeaz[ valoarea 0,752998.
HOUR (or[)
Funcia HOUR returneaz[ num[rul de ore corespunz[toar orei specificate.
Exemplu: HOUR (19:10:30) va returna valoarea 19.
MINUTE (or[)
Funcia MINUTE returneaz[ num[rul de minute corespunz[toare orei specificate.
Exemplu: MINUTE (19:10:30) va returna valoarea 10.
SECOND (or[)
Funcia SECOND returneaz[ num[rul de secunde corespunz[tor orei specificate.
Exemplu: SECOND (19:10:30) va returna valoarea 30.

5.6. Funcţii financiare
Programul Excel pune la dispoziie =i o serie de funcii financiare.
FV (dob`nd[, reper, plat[, vp, tip)

Funcia FV calculeaz[ valoarea viitoare pentru o serie de ]ncas[ri/ pl[i egale
(specificate ]n argumentul plat[), f[cute ]ntr-un num[r de perioade reper, cu o anumit[
dob`nd[ (primul argument). Dob`nda trebuie s[ aib[ aceea=i unitate de m[sur[ ca reper. De
exemplu, dob`nda anual[ trebuie s[ se ]mpart[ la 12 dac[ ]ncas[rile/ pl[ile se fac lunar.
Num[rul vp reprezint[ valoarea prezent[ sau suma care se investe=te/ ]mprumut[ in
momentul iniial. Dac[ vp este omis se consider[ c[ este 0.
Tip poate lua valoarea 0 sau 1. Dac[ are valoarea 0 se consider[ c[ pl[ile se fac la
sf`r=itul perioadei, dac[ are valoarea 1, pl[ile se fac la ]nceputul perioadei. Dac[ argumentul
tip este omis se consider[ c[ are valoarea 0.
Banii care sunt pl[tii sunt reprezentai prin numere negative, iar cei ]ncasai sunt
reprezentai prin numere pozitive.
Exemplu: S[ presupunem c[ o persoan[ vrea s[ investeasc[ bani pentru un proiect
care va fi realizat peste 1 an. De aceea, depune 1 000 $ ]ntr-un cont de economii cu o
dob`nd[ de 6% pe an (dob`nda lunar[ va fi 6%/ 12, adic[ 0.5%). De asemenea, s[
presupunem c[ persoana respectiv[ va depune c`te 100 $ la ]nceputul fiec[rei luni, ]n
urm[toarele 12 luni. C`i dolari vor fi ]n cont la sf`r=itul celor 12 luni?
Aplic[m funcia =FV(0.5%, 12, –100, –1000, 1) obinem 2301.40 $.
PV (dob`nd[, reper, plat[, vv, tip)
Funcia PV calculeaz[ valoarea prezent[ a unui flux de ]ncas[ri/ pl[i viitoare.
Argumentele funciei au aceea=i semnificaie ca =i ]n funcia FV.
Argumentul vv reprezint[ valoarea viitoare, obinut[ dup[ efectuarea ultimei pl[i/
]ncas[ri. Dac[ vv este omis, se consider[ c[ este 0. De exemplu, dac[ vrei s[ economisii 100
000 000 lei pentru un proiect de 20 de ani, atunci 100 000 000 lei este valoarea viitoare.
Banii pl[tii sunt reprezentai prin numere negative, cei ]ncasai prin numere pozitive.
Exemplu: O persoan[ =tie c[ ]=i poate permite s[ pl[teasc[ 220 $ pe lun[ ]n urm[torii
4 ani. Dob`nda curent[ de pia[ este de 9%. C`t de mare este ]mprumutul pe care =i-l permite
persoana ?
Funcia necesar[ pentru calcul este: =PV (0.09/12, 48, –220) care returneaz[ valoarea
8840.65 $.
PMT (dob`nd[, reper, vp, vv, tip)
Funcia PMT calculeaz[ suma care trebuie achitat[ periodic pentru un ]mprumut/
economie, dac[ se indic[ dob`nda, num[rul perioadelor de plat[ (reper).
Argumentele funciei au aceea=i semnificaie ca =i ]n funciile precedente.
Pentru a determina suma total[ de pl[tit pe durata ]mprumutului se ]nmule=te
valoarea returnat[ de funcia PMT cu num[rul de perioade.
Exemple:
1. Ce sum[ trebuie pl[tit[ lunar pentru un ]mprumut de 10 000 $ cu o dob`nd[
anual[ de 8%, care trebuie achitat ]n 10 luni.
Formula de calcul este:
ˆPMT (8%/ 12, 10, 10000) care returneaz[ valoarea –$ 1037.03 dac[ pl[ile se
fac la sf`r=itul lunii.
sau
ˆPMT (8%/ 12, 10, 10000, 0, 1) care returneaz[ valoarea –$ 1,030.16 dac[ pl[ile
se fac la ]nceputul lunii.
S-au obinut valori negative pentru c[ sunt pl[i care trebuie efectuate.
2. Urm[toarea formul[ returneaz[ suma pe care cineva trebuie s[ o primeasc[ lunar,
dac[ a ]mprumutat
5 000 $ cu o dob`nd[ anual[ de 12% pe o perioad[ de 5 luni.

ˆPMT (12%/12, 5, –5000) returneaz[ valoarea 1,030.20.
S-au obinut valori pozitive pentru c[ sunt sume ce trebuie ]ncasate.
3. O persoan[ dore=te s[ str`ng[ 50 000 $ ]n 18 ani prin economisirea unei sume
lunare constante. Dob`nda annual[ este de 6%.
ˆPMT (6%/ 12, 18*12, 0, 50000) care returneaz[ valoarea –129.08 $.
NPV (dob`nd[, valoare1, valoare2, …)
Funcia NPV calculeaz[ valoarea prezent[ actualizat[ a unui flux de venituri/
cheltuieli.
Dac[ n este num[rul de argumente din =irul de valori ( n nu poate fi mai mare de 29),
atunci valoarea net[ actualizat[ se calculeaz[ cu formula:
n

NPV = ∑
i =1

Vi
(1 + dobanda) i

Valorile trebuie s[ fie echidistante ]n timp =i s[ fie valori pl[tite/ ]ncasate la sf`r=itul
fiec[rei perioade.
Dob`nda- reprezint[ dob`nda anual[.
Funcia NPV este asem[n[toare cu PV.
Deosebirea const[ ]n faptul c[ valorile utilizate de PV trebuie s[ fie constante, iar PV
accept[ valori fie la ]nceputul, fie la sf`r=itul perioadei.
Exemplu: Pentru o investiie trebuie pl[tii 10 000 $ timp de 1 an. }n urm[torii trei ani
se obin venituri anuale de 3 000 $, 4 200 $ =i 6 800 $. Dob`nda anual[ este de 10%. S[ se
calculeze valoarea net[ actualizat[ a investiiei.
ˆNPV (10%, –10 000, 3 000, 4 200, 6 800) care returneaz[ valoarea 1,188.44 $
Al doilea argument este negativ pentru c[ reprezint[ o cheltuial[.
IRR (valori, aproximaie)
Funcia IRR calculeaz[ rata intern[ de rentabilitate a unei proiect. Rata intern[ de
rentabilitate este valoarea coeficientului de actualizare (dob`nzii) pentru care venitul net
actualizat este 0.
Valori este o matrice sau un domeniu de celule care conine numerele pentru care
trebuie calculat[ rata intern[ de rentabilitate. Pentru a putea calcula IRR ]n domeniu trebuie
s[ fie cel puin o valoare negativ[ =i cel puin una pozitiv[.
Aproximaie este un num[r care se consider[ a fi cel mai apropiat de rezultatul
furnizat de c[tre funcia IRR.
Microsoft Excel folose=te un algoritm iterativ pentru calcularea valorii IRR. }ncep`nd
cu aproximaia, funcia IRR verific[ toate posibilit[ile de calcul p`n[ c`nd rezultatul este dat
cu o aproximaie de 0.00001%. Dac[ funcia IRR nu g[se=te un rezultat care s[ fie bun dup[
20 de ]ncerc[ri, se va returna valoarea de eroare #NUM!.
}n cele mai multe cazuri nu este nevoie de acest argument. Dac[ aproximaie este
omis, se va considera valoarea implicit[ 10%.
Dac[ IRR returneaz[ eroarea #NUM! Se va ]ncerca din nou cu alte valori pentru
aproximaie.
Exemplu: O persoan[ vrea s[ fac[ o afacere. Pentru ]nceperea afacerii are nevoie de
70 000 $. Veniturile estimate din primii cinci ani sunt: 12 000, 15 000, 18 000, 21 000 =i 26
000 de dolari.

}n domeniul B1:B6 se introduc urm[toarele valori: -70 000, 12 000, 5 000, 18 000, 21
000, 26 000.
Pentru a calcula rata intern[ de rentabilitate a investiiei se folose=te formula:
ˆIRR (B1:B6) care returneaz[ valoarea 8.66%.

5.7. Funcţii de căutare
Dou[ din cele mai utilizate funcii de c[utare din Excel sunt VLOOKUP =i
HLOOKUP.
VLOOKUP (valoare, domeniu, index-linie, tip-c[utare)
HLOOKUP (valoare, domeniu, index-coloan[, tip-c[utare)
Funciile VLOOKUP/ HLOOKUP caut[ valoarea specificat[ ]n primul argument ]n
prima linie/ coloan[ din domeniul specificat ]n al doilea argument. Apoi funcia extrage din
coloana/linia corespunz[toare valorii g[site elementul indicat ]n linia/ coloana specificat[ ]n
al treilea argument- index linie/index coloan[.
Valorile din prima linie/ coloan[ a domeniului trebuie s[ fie ordonata cresc[tor sau
alfabetic.
Argumentul tip-c[utare are o valoare logic[. El este opional. Dac[ lipse=te se
consider[ c[ are valoare TRUE (adev[rat[). Dac[ acest argument are valoare TRUE este
g[sit[ valoarea cea mai mare care este mai mic[ sau egal[ cu valoarea c[utat[. Dac[ are
valoarea FALSE, este c[utat[ valoarea exact[. Dac[ aceast[ valoare nu este g[sit[ ]n prima
linie/coloan[ din domeniul specificat este returnat[ eroarea #N/A.
Aceste funcii sunt folositoare ]n aplicaii de calcul a impozitelor =i a comisioanelor.
Exemplu: Distribuitorii unei firme sunt pl[ii ]n funcie de valoarea v`nz[rilor. Dac[
valoarea v`nz[rilor este mai mic[ de 5 000 000 comisionul este de 0%, ]ntre 5 000 000 =i 30
000 000 comisionul este de 4%, ]ntre 30 000 000 =i 70 000 000 comisionul este de 7%, peste
70 000 000 comisionul este de 10%.

Figura 5.3
}n B2 se introduce formula ˆVLOOKUP (B1, A5:B8, 2). Dac[ ]n B1 se introduce
valoarea 80000000, Excel caut[ aceast[ valoare ]n prima coloan[ din domeniul A5:B8, deci
]n celulele A5, A6, A7, A8, B5, B6, B7, B8. Cum aceast[ valoare nu este g[sit[, funcia
g[se=te cea mai mare valoare care este mai mic[ sau egal[ cu valoarea c[utat[, deci
70000000. Aceast[ valoare se g[se=te pe a patra linie din tabel (linia 8 din Excel). Din aceast[
linie Excel returneaz[ valoarea g[sit[ ]n coloana 2 (al treilea argument), deci 10%.


5.8. Introducerea referinţelor la alte foi de calcul
}ntr-o celul[ se pot introduce =i referine la date din alte foi ale registrului de calcul.
Pentru aceasta se introduce denumirea foii respective, un semn de exclamare =i referina la
celul[. De exemplu: ˆSheet1!A1 ]nseamn[ c[ se face referire la celula A1 din foaia Sheet1.
Dac[ denumirea foii de calcul conine spaii libere, numele acesteia trebuie ]ncadrat
]ntre ghilimele. De exemplu: “Buget 2001”!A1.

5.9. Introducerea de referinţe la alte fişiere
Exist[ situaii ]n care sunt necesare date care se afl[ ]n alt registru de calcul. Pentru a
referi date din alt registru se introduce ]nt`ì numele registrului ]ntre paranteze drepte, numele
foii de calcul, semnul exclam[rii =i referina la celul[. De exemplu: formula
ˆ[vanzari.XLS]Sheet1!A10, face referire la celula A10 din foaia de calcul Sheet1 coninut[ ]n
registrul vanz[ri.XLS.

5.10. Aplicaţii
1. Un ]ntreprinz[tor vrea s[ fac[ o investiie =i face c`teva estim[ri privind valoarea
investiiei, cheltuielile anuale =i veniturile anuale. S[ se determine anul ]n care investiia
devine profitabil[ (anul ]n care venitul total dep[=e=te cheltuielile totale).
Pentru rezolvarea problemei se va crea foaia de calcul din figura 5.4.
Celulele B1, B2, B3 vor conine valorile pentru investiie, cheltuielile anuale =i
venitul anual.
Se genereaz[ ]n coloana A, ]ncep`nd cu celula A6 o serie de numere ]ncep`nd cu
valoarea 0 =i pasul seriei 1.
}n anul 0 cheltuielile totale sunt cele cu investiia, iar venitul total este 0, deci ]n
celula B6 se va introduce formula ˆB1, iar ]n celula C6 valoarea 0.
}n anii urm[tori la cheltuielile totale =i venitul total din anul precedent se adaug[
cheltuielile anuale, respectiv venitul anual. Deci formulele din celulele B7 =i C7 sunt
ˆB6‡B$2, respectiv ˆC6‡B$3. Pentru celulele B2 =i B3 s-a folosit referirea absolut[
deoarece aceste celule trebuie s[ r[m`n[ fixe la copiere (ele conin cheltuielile anuale =i
venitul anual).
Se copiaz[ aceste formule pe coloan[.


Figura 5. 4
}n coloana D se calculeaz[ profitul total (venit total - cheltuieli totale). Se va
introduce ]n celula D6 formula ˆC6-B6. Se copiaz[ aceast[ formul[ pe coloan[.
Pentru a determina pragul de rentabilitate (anul ]n care venitul total dep[=e=te
cheltuielile totale), ]n celula E6 se introduce formula:
ˆif (D6>ˆ0, “<ˆ”, “”).
Deci dac[ veniturile totale sunt mai mari dec`t cheltuielile totale se va afi=a o s[geat[.
Dac[ s-ar copia aceast[ formul[ pe coloan[, s[geata s-ar afi=a ]n dreptul tuturor
lunilor ]n care profitul este pozitiv. Pragul de rentabilitate se obine ]n prima lun[ ]n care
profitul este pozitiv. Deci, pentru a afi=a s[geata doar ]n dreptul acestei luni ]n celula D7 se
va introduce formula:
ˆif (AND(D7>ˆ0,D6<0), “<ˆ”, “”)
Prima lun[ ]n care profitul este pozitiv este testat[ verific`nd profitul din luna
precedent[. Dac[ acesta este negativ, ]nseamn[ c[ avem prima lun[ cu profit, dac[ este
pozitiv ]nseamn[ c[ =i ]n luna precedent[ s-a obinut profit.
Se copiaz[ pe coloan[ formula din celula E7.
2. O firm[ vinde televizoare ]n rate. S[ se determine rata lunar[, totalul de plat[ =i s[
se construiasc[ tabela amortiz[rii ]n cazul ]n care un cump[r[tor achiziioneaz[ un televizor
]n valoare de 5 000 000 lei. Se va considera c[ a fost pl[tit un avans de 500 000 lei =i c[
televizorul va fi pl[tit ]n 12 rate lunare cu o dob`nd[ de 40%. S[ se construiasc[ o foaie de
calcul cu ajutorul c[reia s[ se calculeze automat aceste valori. La proiectarea foii de calcul se
va avea ]n vedere c[ dob`nda se poate modifica ]n timp.


Figura 5. 5
Prima parte a foii de calcul conine datele de intrare ]n problem[: numele
cump[r[torului ( B1), valoarea obiectului cump[rat (B3), data de cump[rare (B4) dob`nda
anual[ (B5) =i num[rul de rate(B6).
}n a doua parte a foii de calcul se va calcula rata lunar[ ce trebuie pl[tit[ ]n ideea c[
dob`nda nu se va modifica. Tot aici se calculeaz[ totalul de plat[ =i valoarea total[ a
dob`nzii. Se vor introduce urm[toarele formule:
B9:ˆ -PMT(B5/12,B6,B3-B7) (rata lunar[)
B10:ˆB11–B3 (totalul de plat[ - valoarea iniial[)
B11:ˆB6*B9 ‡B7 (num[rul de rate*rata lunar[ ‡ avansul)
}n a treia parte a foii de calcul se va crea un tabel care va conine pentru fiecare lun[
data la care trebuie pl[tit[ rata, rata dob`nzii ]n luna respectiv[, restul de plat[, valoarea
dob`nzii =i rata lunar[. Restul de plat[ ]n luna a doua este egal cu restul de plat[ ]n prima
lun[‡valoarea dob`nzii -rata lunar[.Se vor introduce urm[toarele formule:
B14:ˆDATE(year(B$4),MONTH(B$4)‡A14,DAY(B$4))
D14:ˆB3-B7
D15:ˆD14‡F14–E14
E14:ˆ -PMT(C14/12,B$6-A14‡1,D14)
F14:ˆD14*C14/12
Se copiaz[ pe coloan[ formulele din celulele D15, E14, F14, A14. }n domeniul
A14:A25 se genereaz[ o serie numeric[ care ]ncepe de la valoarea 1 =i cu pasul seriei de 1.
3. Un agent economic ]=i propune s[-=i dezvolte activitatea =i are nevoie de un capital
de 240000000 lei. Acest capital este ]mprumutat de la BRD cu o dob`nd[ de 45% =i trebuie
restituit ]n 5 ani. Care este suma lunar[ care trebuie pl[tit[, aici fiind inclus[ at`t dob`nda
compus[ c`t =i plata ]mprumutului?


Figura 5.6
Celulele B1:B3 conin datele de intrare ]n problem[: valoarea ]mprumutului, dob`nda
anual[ =i perioada de restituire.
}n celula B4 se calculeaz[ num[rul de pl[i ]nmulind perioada de restituire cu 12.
Formula din B4 va fi ˆ12*B3.
}n B6 se calculeaz[ rata lunar[ cu formula ˆ -PMT (B2/12, B4, B1)
4. Un proiect necesit[ un volum de investiii de 45.000.000 lei. Durata de execuie a
proiectului este de doi ani, iar durata de via[ economic[ este de 7 ani. Fluxul tran=elor anuale
pentru investiii, cheltuielile de exploatare =i ]ncas[rile sunt cele din tabelul urm[tor:
Anul
Investiii
Cheltuieli de exploatare
}ncas[ri

1
15
-

2
30
-

3

4

5

6

7

8

9

20
40

25
45

25
45

25
47

24
47

24
48

22

S[ se calculeze:
1. Venitul net actualizat cumulat pentru o rat[ de actualizare de 20%
2. Rata intern[ de rentabilitate a proiectului.

Figura 5. 7
Se calculeaz[ pentru fiecare an fluxul de numerar sc[z`nd din ]ncas[ri cheltuielile de
exploatare =i cheltuielile cu investiii (figura 5.7). }n celula B7 se introduce formula ˆB6–
B5–B4. Se copiaz[ formula la domeniul C7:J7.
}n celula C9 se calculeaz[ venitul net actualizat cumulat cu formula ˆNPV(B1,B7:J7).
}n celula C10 se calculeaz[ rata intern[ de rentabilitate cu formula ˆIRR(B7:J7).

5. Un ]ntreprinz[tor care face o investiie ]ntr-un obiectiv economic c`=tig[ un venit
net anual de 200000 lei, timp de 12 ani c`t este durata de funcionare a obiectivului. Care este
valoarea prezent[ a acestui flux de venituri ]n momentul investiiei, la o valoare de discontare
de 14%.

Figura 5. 8
}n celula B5 se va introduce formula: ˆ PV (B3, B2, B1), unde B3 reprezint[
dob`nda, B2 perioada ]n care se obin veniturile, B1 valoarea venitului anual.
6. O echip[ de muncitori este pl[tit[ ]n funcie de num[rul de ore lucrate. Orele
lucrate peste programul normal de lucru (8 ore) sunt pl[tite dublu. S[ se calculeze cu c`t este
pl[tit zilnic fiecare muncitor, cunosc`nd tariful orar =i orele de intrare =i ie=ire din tur[.
Pentru rezolvarea problemei se va folosi foaia de calcul din figura 5.9.
Pentru fiecare muncitor, se calculeaz[ ]n coloana E num[rul de ore lucrate. Formula
utilizat[ ]n celula E4 este ˆD4-C4, formul[ care se copieaz[ ]n domeniul E5:E8.
}n coloana F se afi=eaz[ salariul calculat pentru orele lucrate ]n fiecare zi. Formula din
celula F4 este:
ˆIF(HOUR(E4)‹8,HOUR(E4)*B$1‡MINUTE(E4)*B$1/60, 8*B$1‡(HOUR(E4)-8)*2*B$1‡
MINUTE(E4)*2*B$1/60)
Aceast[ formul[ se copieaz[ ]n domeniul F5:F8.
Dac[ ]n funcia IF ar fi fost utilizat[ condiia E4‹8, ar fi fost incorect. E4‹8 este
]ntotdeauna adev[rat[, deoarece ]n E4 avem o or[ =i se =tie c[ numerele seriale ata=ate orelor
sunt mai mici dec`t 1, deci =i mai mici dec`t 8. Pentru a extrage num[rul de ore lucrate s-a
folosit funcia HOUR.

Figura 5.9
7. Un registru Excel este alc[tuit din dou[ foi de calcul. O foaie de calcul – cursuri conine cursurile de schimb pentru mai multe valute, cealalt[ foaie – casa – este folosit[
pentru a calcula echivalentul ]n lei al sumelor schimbate.

Foaia de calcul cursuri are structura din figura 5.10.

Figura 5.10
Foaia de calcul casa are structura din figura 5.11.

Figura 5.11
}n coloana Nume se introduce numele persoanei care realizeaz[ o tranzacie, iar ]n
coloana Tranzacie se introduce tipul tranzaciei efectuate. Valorile permise ]n aceast[
coloan[ sunt C – pentru cump[rare =i V – pentru v`nzare.
}n coloana Tip valut[ se introduce numele monedei schimbate (atenie, numele
monedei trebuie s[ fie identic cu cel din foaia de calcul cursuri).
}n coloana Suma schimbat[ se introduce suma care se schimb[.
}n coloana Echivalent lei se calculeaz[ echivalentul ]n lei al sumei schimbate (]n
funcie de valut[, suma schimbat[ =i tipul tranzaciei). Formula utilizat[ ]n celula E2 este:
ˆD2*VLOOKUP(C2, cursuri!A$2:C$9, IF(B2ˆ”C”,2,3))
Se copieaz[ formula pe coloan[, =i pe m[sur[ ce se introduc date ]n foaia de calcul,
echivalentul ]n lei al sumei schimbate se va calcula automat.

Calcule cu matrici

CAPITOLUL 6
CALCULE CU MATRICI
6.1. Calcule cu matrici
Matricile sunt domenii dreptunghiulare de formule sau valori pe care Excel le trateaz[
ca fiind un grup. Unele funcii =i formule care lucreaz[ cu astfel de elemente returneaz[
rezultate care sunt plasate ]n mai multe celule. Altele, de=i prelucreaz[ matrici de valori, pot
furniza un rezultat afi=at ]ntr-o singur[ celul[.
Pentru a introduce o formul[ de tip matrice se parcurg urm[toarele etape:
1. Se selecteaz[ domeniul care va conine formula de tip matrice.
2. Se introduce formula.
3. Dup[ introducerea formulei se apas[ combinaia de taste <Shift> + <Ctrl> +
<Enter>.
Foaia de calcul urm[toare (figura 6.1) conine un exemplu cu datele care sunt
introduse ]ntr-o factur[:

Figura 6.1
Pentru a calcula totalul ]n coloana D se pot folosi =i metodele anterioare (]n celula D4
se introduce formula =B4*C4, care apoi se copiaz[ ]n celelalte celule din coloana D). }n locul
acestor formule se poate introduce o singur[ formul[, valabil[ ]n tot domeniul D4:D6, care va
ocupa mai puin[ memorie.
Pentru a calcula totalul utiliz`nd formule de tip matice:
1. Se selecteaz[ domeniul D4:D6.
2. Se introduce ]n linia de formul[, formula = B4:B6*C4:C6
3. Se tasteaz[ combinaia de taste <Shift> + <Ctrl> + <Enter>.
}n bara de formul[, formula va fi afi=at[ ]ntre acolade {}. Fiecare celul[ a domeniului
D4:D6 conine aceea=i formul[. Acoladele simbolizez[ c[ formula este o matrice =i c[
domeniul matrice trebuie s[ fie tratat ca o entitate unic[. Nu se pot introduce linii sau coloane
]n acest domeniu dup[ cum nu este posibil[ =tergerea componentelor sale sau editarea unei
singure celule. Formula nu multiplic[ valorile din dou[ celule, ci valorile din dou[ matrici,
B4:B6 =i C4:C6, f[c`nd corespondena corect[ a elementelor acestora B4*C4, B5*C5,
B6*C6.
Rezultatele sunt plasate ]n celulele matricei D4:D6 selectat[ anterior.
Domenii de tip matrice se pot utiliza =i ca argumente la funcii. Funciile cu
argumente de tip matrice se introduc la fel ca =i formulele de acest tip.
1. Se selecteaz[ un domeniu de dimensiuni corecte.
2. Se introduce funcia specific`nd domeniile de celule asupra c[rora opereaz[.
3. Se apas[ combinaia <Shift> + <Ctrl> + <Enter>.

De exemplu, dac[ ]n exemplul anterior trebuie calculat totalul general f[r[ a calcula
totalurile pariale, ]n celula D7 trebuie introdus[ formula {=SUM(B4:B6*C4:C6)}.
Introducerea se termin[ cu <Shift> + <Ctrl> + <Enter> pentru ca formula s[ fie considerat[
ca formul[ de tip matrice.
}n mod uzual domeniul utilizat pentru introducerea formulelor sau funciilor de tip
matrice trebuie s[ fie corect selectat. Dac[ domeniul de tip matrice selectat este prea mic, nu
se pot vedea rezultatele; dac[ este prea mare, celulele care nu au fost utilizate vor conine
mesajul #N/A.

6.2. Funcţii pentru matrici
Funciile de lucru cu matrici cele mai utilizate sunt:
MDETERM (matrice)
Funcia MDETERM calculeaz[ determinantul unei matrici.
MINVERSE (matrice)
Funcia MINVERSE calculeaz[ inversa unei matrici.
MMULT (matrice1, matrice2)
Funcia MMULT efectueaz[ ]nmulirea a dou[ matrici. Num[rul de coloane din
matrice1 trebuie s[ fie egal cu num[rul de linii din matrice2.
TRANSPOSE (matrice)
Funcia TRANSPOSE efectueaz[ operaia de transpunere a unei matrici.
Dac[ ]ntr-o formul[ intervine o funcie de tip matrice, introducerea formulei se
termin[ tast`nd combinaia de taste <Shift> + <Ctrl> + <Enter>.
Exemplul urm[tor prezint[ modul ]n care se poate calcula inversa unei matrici.
Matricea iniial[ este cuprins[ ]n domeniul A2:C4 (figura 6.2).

Figura 6.2
Pentru a calcula inversa matricei se selecteaz[ domeniul A7:C9 (]n acest domeniu se
va afi=a rezultatul), se introduce formula =i =MINVERSE(A2:C4) =i se apas[ <Shift> +
<Ctrl> + <Enter>.

Calcule cu matrici

6.3. Aplicaţie
Firma ABC vinde ap[ mineral[, sucuri =i vin ]n Rom`nia =i Moldova. Foaia de calcul
din figura 6.3 conine situaia v`nz[rilor din anii 1999 =i 2000.
S[ se calculeze valoarea medie a v`nz[rilor pentru Romania =i Moldova pe ce doi ani.

Figura 6.3
Pentru a calcula valoarea medie a v`nz[rilor pentru Rom`nia =i Moldova se introduc
formulele:
Celula C18: ˆ AVERAGE(IF($B5:$B14ˆ”Romania”,C5:C14)). Se termin[ formula
de introdus cu <Shift> + <Ctrl> + <Enter>. Se copieaz[ formula ]n D18. Deci se va
calcula media aritmetic[ doar a valorilor care ]n domeniul B5:B14 conin textul Romania.
Celula C19: ˆ AVERAGE(IF($B5:$B14ˆ”Moldova”,C5:C14)). Se termin[ formula
de introdus cu <Shift> + <Ctrl> + <Enter>. Se copieaz[ formula ]n D19. Deci se va
calcula media aritmetic[ doar a valorilor care ]n domeniul B5:B14 conin textul Moldova.

Sistemul de gestiune al graficelor

CAPITOLUL 7
SISTEMUL DE GESTIUNE AL GRAFICELOR
7.1. Sistemul de gestiune al graficelor
Utiliz`nd Excel, datele din tabele pot fi reprezentate sub form[ grafic[. Un grafic este
un instrument eficient pentru prezentarea clar[ a datelor, ]ntr-un mod care ofer[ un impact
vizual imediat. Cu alte cuvinte, graficele sunt mai u=or de ]neles “dintr-o privire” dec`t
liniile =i coloanele de date. }n Excel se pot crea mai multe tipuri de grafice. Unele din ele sunt
bidimensionale (2D), altele tridimensionale (3D).
Principalele tipuri de grafice sunt:
• Arie - Area
• Bar[ - Bar
• Coloan[ - Column
• Linie - Line
• Circulare - Pie
• Inel - Doughnut
• Radar - Radar
• XY (Dispersate) – Scatter
• Suprafa[ - Surface
• Cilindru – Cylinder
• Cone – Con
• Piramid – Piramid[
Tipuri de grafice tridimensionale:
• Zon[
• Bar[
• Coloan[
• Linie
• Pl[cint[
• Suprafa[
Pentru majoritatea tipurilor de grafice, exist[ cel puin dou[ variante sau subtipuri.
Un grafic bidimensional este desf[=urat pe dou[ axe:
• axa orizontal[ - axa X, numit[ =i axa categoriilor
• axa valorilor – axa Y, pe care sunt reprezentate seriile de date. O serie de date este un set
de valori care descriu evoluia unei m[rimi.
La graficele 3D este utilizat[ pentru a treia dimensiune axa Z.
Un grafic conine mai multe obiecte care pot fi selectate =i modificate individual.
Figura urm[toare (figura 7.1) prezint[ unele din aceste obiecte.
Titlu
Axa Y
Legenda

Grafic

Axa X
Figura 7.1

}n continuare este prezentat[ o descriere sumar[ a principalelor tipuri de grafice.

7.2. Graficele de tip arie - Area
Un grafic arie ilustreaz[ continua schimbare ]n volum a unor serii de date. Acest tip
de grafic ]nsumeaz[ datele din toate seriile individuale pentru a crea linia de v`rf care
cuprinde zona, oferind privitorului o imagine asupra modului ]n care diferitele serii contribuie
la volumul total. Utilizai graficul arie pentru cifrele referitoare la v`nz[ri =i la producie,
pentru a ar[ta modul ]n care volumul se modific[ ]n timp =i pentru a evidenia cantitatea sau
volumul schimb[rii.

Figura 7.2

7.3. Grafice bară - Bar
Un grafic bar[ este utilizat pentru compararea obiectelor neconectate ]n timp. Acest
tip de grafic nu ofer[ o imagine prea bun[ a evoluiei ]n timp, el utilizeaz[ bare orizontale
pentru a ar[ta variaia pozitiv[ sau negativ[ fa[ de un punct de referin[. Barele aflate la
st`nga punctului de referin[ arat[ o variaie negativ[, iar cele din dreapta arat[ o variaie
pozitiv[.

Figura 7.3

7.4. Grafice coloană - Column
Graficele coloan[ sunt ]n general folosite pentru a ar[ta variaia ]n timp a unor m[rimi
necontinue. Acest tip de diagram[ utilizeaz[ bare verticale pentru a da impresia de m[sur[tori
f[cute la intervale de timp diferite. Graficele coloan[ sunt folosite frecvent pentru comparea
diferitelor elemente prin plasarea lor unele l`ng[ altele.
Asem[n[toare cu graficele coloan[ sunt graficele de tip cilindru, con =i piramid[, numai c[ la
aceste grafice valorile nu mai sunt reprezentate prin coloane ci prin cilindre, conuri, respectiv
piramide.


Figura 7.4
Asem[n[toare sunt graficele de tip cilindru, con, piramid[. Diferena este c[ valorile
nu mai sunt reprezentate prin coloane, ci prin cilindrii, conuri, piramide.

7.5. Grafice linie - Line
Un grafic linie ilustreaz[ evoluia unei m[rimi la care intervalele de variaie sunt
egale. Dac[ intervalele de variaie sunt neegale se va utiliza un grafic (dispersat) XY. Pentru
fiecare serie de date se va obine ]n grafic o linie.

Figura 7.5

7.6. Grafice circulare - Pie
}ntr-un grafic circular se evideniaz[ m[rimea p[rilor ]n raport cu ]ntregul. }ntr-un
astfel de grafic se poate reprezenta o singur[ serie de date. Pentru a scoate mai bine ]n
eviden[ valorile pe care le reprezint[, sectoarele din grafic pot fi scoase ]n afara cercului.
Pentru a scoate ]n afar[ un sector dintr-un grafic circular, se aplic[ un clic pe suprafaa
sectorului pentru a selecta ]ntregul grafic, apoi un al doilea clic pentru a selecta numai
sectorul, dup[ care se trage sectorul ]n afara cercului. Se elibereaz[ butonul mouse-ului atunci
c`nd sectorul este poziionat ]n locul dorit.


Figura 7.6

7.7. Grafice inel - Doughnut
La fel ca =i graficele circulare, graficele inel scot ]n eviden[ m[rimea p[rilor dintrun ]ntreg. Deosebirea este c[ structura diagramelor inel permite reprezentarea mai multor
serii de date. Fiecare inel concentric conine datele dintr-o serie de date.

Figura 7.7

7.8. Grafice radar - Radar
Fiecare categorie (fiecare etichet[ care ar fi afi=at[ pe axa X la un grafic ]n dou[
dimensiuni) are propria ax[. Punctele de date sunt plasate de-a lungul acestor axe. Un grafic
radar rezult[ prin unirea punctelor de date care au aceea=i semnificaie pe toate axele.

Figura 7.8

7.9. Grafice XY (Dispersate) - Scatter
Un grafic XY (Dispersat) este asem[n[tor cu unul linie, numai c[ ilustreaz[ evoluia
unor m[rimi la care intervalele de variaie nu sunt egale.


Figura 7.9

7.10. Crearea unui grafic
O metod[ pentru realizarea automat[, pas cu pas, a unei diagrame pornind de la datele
din foaia de calcul este folosirea aplicaiei Chart Wizard. Graficele se pot crea ]n foaia de
calcul curent[ sau se pot plasa ]ntr-o nou[ foaie de calcul din registrul curent.
Foaia de calcul urm[toare (figura 7.10) conine v`nz[rile dintr-o libr[rie pentru c`teva
articole, pe durata unei s[pt[m`ni.

Figura 7.10
Pe baza acestui tabel se pot construi dou[ grafice
Primul grafic (figura 7.11) conine trei serii de date: v`nz[rile pentru creioane, caiete

=i pixuri. Pentru fiecare zi valorile fiec[rei serii sunt reprezentate prin bare colorate ]n mod
diferit. Barele de aceea=i culoare fac parte din aceea=i serie.
Figura 7.11

Al doilea grafic (figura 7.12) conine cinci serii de date: v`nz[rile efectuate luni, mari,
miercuri, joi =i vineri. }n grafic sunt reprezentate v`nz[rile efectuate ]n fiecare zi pentru
fiecare articol.

Figura 7.12
Dac[ analiz[m modul ]n care sunt generate seriile constat[m c[ la primul grafic seriile
sunt generate pe linii, la al doilea grafic seriile sunt generate pe coloane. Deci, ]n funcie de
cum se genereaz[ seriile se obin grafice diferite.
Dac[ num[rul de linii este mai mare dec`t num[rul de coloane Excel va ]ncerca s[
genereze seriile pe coloane, altfel va genera seriile pe linie. Acesta este modul ]n care Excel
]ncearc[ automat s[ genereze graficele, dar modul ]n care se se vor genera seriile poate fi
specificat de c[tre utilizator.
Primul pas ]n crearea unui grafic este selectarea datelor din foaia de calcul. Pentru
selectarea datelor se vor respecta urm[toarele reguli:
• Datele pentru grafic trebuie s[ fie introduse ]n linii =i coloane, care nu trebuie nep[rat s[
fie adiacente(celulele nediacente se selecteaz[ in`nd ap[sat[ tasta <Ctrl>).
>
• Etichetele (textele) ce vor fi folosite ]n grafic vor fi plasate primele linii =i primele
coloane ale tabelului.
Pentru exemplul nostru vom selecta domeniul A1:F4.
Dup[ selectarea datelor se face un clic pe butonul Chart Wizard. Pe ecran va apare
prima fereastr[ din Chart Wizard – Step 1 of 4 (figura 7.13).
Din aceast[ fereastr[ se va selecta tipul graficului. }n fereastr[ exist[ dou[ butoane:
Standard Types =i Custom Types. C`nd este selectat butonul Standard Types apare o list[
cu toate tipurile standard de grafice. Pentru fiecare tip de grafic exist[ mai multe subtipuri.
Dac[ este selectat butonul Custom Types apare o list[ de grafice predefinite. Din una din
cele dou[ liste se selecteaz[ tipul de grafic dorit.
Pentru exemplul nostru vom selecta un grafic de tip coloan[ (Column).
}n partea de jos a ferestrei apar trei butoane:
Next
– pentru a trece la pasul urm[tor.
Back
– pentru a reveni la pasul anterior.
Finish – se creaz[ graficul folosind opiunile selectate p`n[ la acel moment.
Cancel – se renun[ la crearea graficului


figura 7.14 – caseta Chart Wizard – Step 1 of 4
Se selecteaz[ butonul Next pentru a trece la urm[toarea fereastr[ din ChartWizard – Step 2
of 4.
Aceast[ caset[ de dialog are dou[ butoane ]n partea de sus a casetei. Se selecteaz[
butonul Data range. Pe ecran apare urm[toarea caset[ de dialog (figura 7.14):

Figura 7.14 - ChartWizard – Step 2 of 4

}n caseta Data range este afi=at domeniul de celule din care se va genera graficul. Dac[ nu
apare domeniul corect, se poate introduce alt domeniu (cu ˆ ]n fa[).
Din lista de opiuni Series in se selecteaz[ Rows dac[ seriile de date se vor genera pe linii =i
Columns dac[ seriile de date se vor genera pe coloane.
Pentru exemplul nostru ]n Data range trebuie s[ avem domeniul = A1:F4.
Vom genera seriile pe linie, deci se selecteaz[ opiunea Rows.
Se selecteaz[ butonul Series. Pe ecran apare urm[toarea caset[ de dialog (figura 7.15):

Figura 7.15 – Step 2 of 4 – Chart Source Data
}n lista Series sunt afi=ate seriile de date ale graficului. Dac[ se selecteaz[ o serie ]n
caseta text Name apare sau numele seriei, sau celula care conine numele seriei, iar ]n caseta
Values este afi=at domeniul de valori din care se genereaz[ seria.
Pentru exemplul nostru, dac[ select[m seria caiete, ]n caseta Name va apare =Sheet1!$A$3
(A3 este celula care conine numele seriei), iar ]n caseta Values va apare =
Sheet1!$B$3:$F$3 (setul de valori din care se genereaz[ seria).
}n caseta text Category(x) axis labels se introduce domeniul care conine informaiile
ce vor fi afi=ate pe axa x (a categoriilor).
}n cazul nostru ]n aceast[ caset[ apare = Sheet1!$B$1:$F$1. Aceste celule conin zilele
s[pt[m`nii ce vor fi afi=ate pe axa x.
O serie poate fi =tears[ dac[ atunci c`nd este selectat[ se apas[ pe butonul Remove.
Pentru a ad[uga o serie nou[ se apas[ pe butonul Add; ]n caseta Name se scrie numele seriei,
iar ]n caseta Values valorile care genereaz[ seria.
}n casetele Name, Values =i Category(x) axis labels celulele sau domeniile trebuie
s[ aib[ specificate ]n fa[ =i numele foii de calcul (numele foii de calcul este separat de
referinele celulelor prin !).
Se apas[ pe butonul Next.
Pe ecran apare caseta de dialog Step 3 of 4 - Chart Options.

Aceast[ caset[ de dialog are ]n partea de sus mai multe butoane din care pot fi setate diferite
caracteristici ale graficului.
Butonul Axes
C`nd este ap[sat acest buton apare urm[toarea caset[ de dialog (figura 7.16):

Figura 7.16
•
•

Dac[ este selectat[ opiunea Category(x) axis ]n grafic vor fi afi=ate informaiile de pe
axa X, ]n caz contrar pe axa X nu se va afi=a nimic.
Dac[ este selectat[ opiunea Value(y) axis ]n grafic vor fi afi=ate informaiile de pe axa
Y, ]n caz contrar pe axa Y nu se va afi=a nimic.

Butonul Titles
C`nd este ap[sat acest buton pe ecran apare urm[toarea caset[ de dialog (figura 7.17):

Figura 7.17

}n caseta Chart title se introduce titlul graficului.
}n caseta Category(x) axis se introduce titlul axei x.
}n caseta Category(y) axis se introduce titlul axei y.
}n cazul ]n care graficul are dou[ axe X sau Y, ]n urm[toarele dou[ casete text se introduc
titlurile asociate acestora.
Butonul Gridlines
C`nd acest buton este ap[sat, pe ecran apare urm[toarea caset[ de dialog (figura 7.18):

Figura 7.18
}n aceast[ caset[ se specific[ dac[ sunt afi=ate sau nu liniile de reea. Liniile de reea
sunt linii orizontale =i verticale dispuse pe ]ntreaga suprafa[ a graficului. Ele sunt folosite
pentru a citi mai u=or valorile de pe grafic. Exist[ dou[ tipuri de linii de reea:
• Principale (Major Gridlines)-pentru delimitarea intervalelor principale de pe axe.
• Secundare (Minor Gridlines)-pentru a insera linii de reea ]ntre intervalele principale de
pe axe.
Dac[ trebuie afi=ate liniile de reea principale se vor marca casetele Major Gridlines,
dac[ trebuie afi=ate liniile de reea secundare se vor marca casetele Minor Gridlines.
Butonul Legend
La ap[sarea acestui buton pe ecran apare urm[toarea caset[ de dialog (figura 7.19):

Figura 7.19

Dac[ opiunea Show Legend este setat[, graficul va avea ata=at[ o legend[. Poziia ]n grafic
a legendei se stabile=te cu una din opiunile din domeniul Placement.
Opiune
Bottom
Corner
Top
Right
Left

Locul de plasare a legendei
}n partea de jos a graficului
}n colul din dreapta-sus al graficului
}n partea de sus a graficului
}n partea dreapt[ a graficului
}n partea st`ng[ a graficului

Butonul Data labels
La ap[sarea acestui buton pe ecran apare urm[toarea caset[ de dialog (figura 7.20):

Figura 7.20
Folosind una din opiunile din domeniul Data labels, barelor din grafic li se pot asocia ni=te
etichete. Aceste etichete pot conine fie valorile punctelor de date din grafic, fie categoria pe
care o reprezint[.
Butonul Data Table
C`nd acest buton este ap[sat, pe ecran apare urm[toarea caset[ de dialog (figura 7.21):

Figura 21

Dac[ opiunea Show Data Table este setat[, sub grafic va fi afi=at tabelul pe baza c[ruia este
construit graficul.
Se apas[ pe butonul Next.
Pe ecran apare caseta de dialog Step 4 of 4 - Chart Location (figura 7.22).

Figura 7.22 – caseta de dialog Step 4 of 4 - Chart Location
}n aceast[ caset[ de dialog se specific[ unde va fi plasat graficul.
Dac[ este selectat[ opiunea As new sheet - graficul se va crea ]ntr-o nou[ foaie de calcul al
c[rei nume este specificat ]n caseta text al[turat[.
Dac[ este selectat[ opiunea As object in - se va crea ]n foaia de calcul specificat[ ]n caseta
text al[turat[.
Se apas[ pe butonul Finish.

7.11. Mutarea şi dimensionarea unui grafic
Dup[ crearea unui grafic, acesta poate fi m[rit sau mic=orat sau poate fi mutat ]n alt[
poziie ]n foaia de calcul.
Pentru a dimensiona un grafic:
1. Se selecteaz[ graficul aplic`nd un clic deasupra lui. }n jurul graficului vor apare mici
p[trate negre, numite puncte de selectare.
2. Se plaseaz[ cursorul mouse-ului deasupra unui punct de selectare. Cursorul ]=i va
modifica forma – va c[p[ta forma unei s[gei cu dou[ v`rfuri.
3. Se aplic[ un clic =i se trage de acest cursor pentru a m[ri sau mic=ora graficul. Pentru a
modifica dimensiunile graficului ]n mod proporional se va ine ap[sat[ tasta <Shift> ]n
>
timp ce se trage de unul din punctele de selectare din coluri.
Pentru a muta un grafic ]n alt[ poziie a foii de calcul:
1. Se selecteaz[ graficul aplic`nd un clic deasupra lui. }n jurul graficului trebuie s[ apar[
punctele de selectare.
2. Se aplic[ un clic ]n interiorul graficului =i se trage graficul ]n noua poziie. }n timpul
acestei operaii cursorul ia forma unei cruci cu s[gei.

7.12. Modificarea tipului de grafic
La crearea unui grafic se selecteaz[ un anumit tip de grafic. Dup[ finalizarea graficului,
tipul acestuia poate fi modificat ]n modul urm[tor:
1. Se selecteaz[ graficul.
2. Din bara de instrumente Chart se selecteaz[ butonul Chart Type.
3. Din lista care apare se selecteaz[ tipul de grafic dorit.


Tipul de grafic se poate modifica =i cu ajutorul opiunilor din meniu.
1. Se selecteaz[ graficul.
2. Se aplic[ un clic pe butonul din dreapta al mouse-ului, =i din meniul care apare se
selecteaz[ opiunea Chart Type.
Pe ecran apare urm[toarea caset[ de dialog (figura 7.23),

Figura 7.23
asem[n[toare cu caseta de dialog din care se stabile=te tipul graficului la crearea lui. Se
selecteaz[ tipul de grafic dorit.

7.13. Opţiuni pentru afişarea tridimensională
Pentru a modifica unghiurile, ]n[limea =i perspectiva tipului de grafic se folose=te
comanda 3-D View care apare ]n meniul rapid afi=at la aplicarea uniu clic pe butonul din
dreapta al mouse-ului.
Pe ecran apare urm[toarea caset[ de dialog (figura 7.24):

Figura 7.24 – caseta de dialog 3-D View

Butoanele pentru ]n[lime (Elevation) controleaz[ nivelul relativ la care este v[zut[
diagrama. Pentru a modifica valoarea existent[ se pot folosi cele dou[ butoane sau se poate
introduce o nou[ valoare ]n caseta Elevation.
Butoanele pentru rotaie controleaz[ unghiul de afi=are al diagramei ]n jurul unei axe
verticale. O alt[ probabilitate de modificare a valorii existente este introducerea noului unghi
]n caseta Rotation.
Dac[ opiunea Right Angle Axis nu este selectat[, ]n caseta de dialog apar =i
butoanele pentru perspectiv[. Aceste butoane sunt folosite pentru a stabili profunzimea ]n
care este prezentat graficul. }n acela=i scop este folosit[ =i valoarea introdus[ ]n caseta
Perspective.
Dac[ opiunea Auto Scaling este selectat[, cele dou[ dimensiuni ale graficului (baza
=i ]n[limea) se vor stabili automat de c[tre Excel.
Dac[ opiunea Auto Scaling nu este selectat[, se activeaz[ caseta text Height ]n care
se specific[ raportul ]n[lime/ baz[ ]n procente.
Se selecteaz[ butonul OK.

7.14. Modificarea caracteristicilor unui grafic
Aproape orice parte a unui grafic Excel poate fi formatat[. Aceast[ flexibilitate ofer[
un control total asupra aspectului graficului creat. Se pot modifica culorile, ha=urile, fonturile
diferitelor elemente dintr-un grafic. Pentru a putea fi formatat, orice element din grafic
trebuie ]nt`i selectat. Selectarea se face foarte u=or cu ajutorul mouse-ului aplic`nd un clic
peste elementul respectiv, dup[ ce graficul a fost selectat. Dup[ selectarea elementului dorit
se apas[ butonul din dreapta al mouse-ului =i se aplic[ comanda Format ‡ numele
elementului selectat. }n funcie de obiectul selectat pe ecran apare o caset[ de dialog care, ]n
general, ]n partea superioar[ are mai multe butoane. Din aceste casete de dialog se selecteaz[
caracteristicile graficului.

7.15. Aplicaţie – grafice tip plăcintă
Foaia de calcul urm[toare (figura 7.25) conine cheltuielile pe care le face o firm[
pentru a-=i face reclam[.

Figura 7.25
S[ se reprezinte ]ntr-un grafic structura acestor cheltuieli.
Cel mai potrivit tip de grafic pentru a reprezenta structura acestor cheltuieli este
graficul Pie.
S[ calcul[m ]n coloana C c`t la sut[ din valoarea total[ reprezint[ fiecare tip de
cheltuial[. }n celula C4 vom introduce formula =B4/B$8 (cheltuielile/cheltuielile totale) =i

copiem formula ]n domeniul C5:C7. Pentru ca numerele s[ fie afi=ate sub form[ de procent,
le select[m =i le format[m de tip procent.
Pentru construirea graficului:
1.
Se selecteaz[ zona A4:B7.
2.
Se apas[ pe butonul Chart Wizard.
3.
Se alege un grafic de tip Pie. Se selecteaz[ un subtip de grafic care s[ afi=eze =i
procentele.
4.
Avem o singur[ serie de date ]n domeniul B4:B7. Deci seria se va genera pe coloan[
=i domeniul de valori este B4:B7.
Din celulele specificate ]n Category(x) axis labels se vor extrage numele sectoarelor.
Deci ]n cazul nostru complet[m cu A4:A7.
Se obine urm[torul grafic (figura 7.26):

Figura 7.26
Dup[ construirea graficului compar[m procentele din coloana C cu procentele din
dreptul sectoarelor. Constat[m c[ sunt exact acelea=i valori.
Deci fiecare sector reprezint[ un procent dintr-un ]ntreg.

7.16. Aplicaţie – grafice de tip linie
Foaia de calcul urm[toare (figura 7.27) conine valoarea v`nz[rilor efectuate ]n
perioada 1994-1998 de o firm[ distribuitoare de produse soft.

Figura 7.27
Pentru a ilustra tedinele de variaie ]n timp se va folosi un grafic de tip linie (nu XY
pentru c[ intervalele de timp sunt egale).

Pentru a crea graficul:
1.
Se selecteaz[ domeniul A3:F6
2.
Se selecteaz[ butonul Chart Wizard.
3.
Se selecteaz[ un grafic de tip Line.
4.
}n grafic vom avea trei serii de date, pentru v`nz[rile de Excel, a doua pentru
v`nz[rile de Word, a treia pentru Power Point.
Deci seriile se vor genera pe linie.
Avem trei serii:
1.
Excel - ]n domeniul B4:F4
2.
Word - ]n domeniul B5:F5
3.
Power Point - ]n domeniul B6:F6
Pe axa x trebuie afi=ai anii. Deci ]n Category(x) axis labels complet[m = B3:F3.
Se va obine urm[torul grafic (figura 7.28):

Figura 7.28

7.17. Aplicaţie – grafice Stacked Line
Foaia de calcul urm[toare (figura 7.29) conine num[rul de calculatoare asamblate
]ntr-o fabric[ ]n trei intrvale de timp: de la ora 8 la ora 16 =i de la ora 16 la ora 24, de luni
p`n[ vineri.

Figura 7.29
S[ se reprezinte ]ntr-un grafic num[rul total de calculatoare asamblate la sf`r=itul fiec[rei
perioade.
La sf`r=itul perioadei 8-16 num[rul total de calculatoare asamblate este egal cu suma dintre
num[rul de calculatoare asamblate ]n intervalul 0-8 cu cele asamblate ]n intervalul 8-16, iar la
sf`r=itul zilei trebuie ]nsumate calculatoarele asamblate ]n cele trei perioade.
Cel mai potrivit tip de grafic este Stacked Line. La acest tip de grafic linia pentru o serie se
genereaz[ adun`nd =i valorile din seriile precedente.

1.
2.
3.
4.

Se selecteaz[ domeniul A1:F4
Se selecteaz[ butonul Chart Wizard.
Select[m un grafic de tip linie =i ca subtip un grafic Stacked Line.
}n grafic avem trei serii de date:
0 - 800
800 – 1600
1600 - 2400

]n B2:F2
]n B3:F3
]n B4:F4

Seriile sunt generate pe linie.
Pe axa x vor fi afi=ate zilele s[pt[m`nii, deci ]n Category(x) axis labels vom introduce
domeniul = B1:F1.
Se va obine urm[torul grafic (figura 7.30).

Figura 7.30

7.18. Aplicaţie –grafice de tip xy dispersate (Scater)
Foaia de calcul urm[toare (figura 7.31) conine nivelul stocurilor pentru articolele realizate de
o fabric[ de ]nc[l[minte pe durata unei linii.

Figura 7.31
S[ se reprezinte sub form[ grafic[ nivelul stocurilor pentru cele trei articole.
Deoarece datele sunt distribuite inegal trebuie aleas[ o diagram[ xy =i nu una de tip linie.
1.
Se selecteaz[ domeniul A1:I4
2.
Se selecteaz[ un grafic de tip xy
3.
Seriile de date se vor genera pe linie.
4.
Vom avea 3 serii:

Sandale
B2:I2
Adida=i
B3:I3
Pantofi
B4:I4
Pe axa x vor fi afi=ate zilele, deci ]n Category(x)Axis Labels vom avea = B2:I1
Se va obine urm[torul grafic (figura 7.32):

Figura 7.32

Liste

CAPITOLUL 8
LISTE
8.1. Crearea şi editarea unei liste
}n Excel datele pot fi gestionate cu u=urin[ dac[ sunt organizate sub form[ de liste.
O list[ reprezint[ o zon[ dintr-o foaie de calcul care conine date similare. Fiecare coloan[
din list[ reprezint[ o anumit[ categorie de date (numit[ c`mp) =i determin[ tipul de
informaie necesar pentru fiecare intrare ]n list[. Fiecare linie dintr-o list[ constituie o
]nregistrare.
Pentru a crea o list[ se introduce un titlu pentru fiecare coloan[. Listele se pot crea ]n
orice zon[ din foaia de calcul, trebuie doar ca zona de sub list[ s[ nu conin[ date, astfel
]nc`t lista s[ se poat[ ]ntinde f[r[ s[ interfereze cu alte date din foaia de calcul.
Pentru a introduce ]nregistr[ri ]n list[ se vor introduce date ]n liniile imediat de sub
titlurile coloanelor. Fiecare ]nregistrare trebuie s[ conin[ acelea=i c`mpuri. }n figura 8.1
este prezentat[ o list[ care conine informaii despre comenzile livrate de o firm[
distribuitoare de produse electrocasnice la firme din diverse ora=e din ar[. Pentru fiecare
comand[ sunt furnizate informaii despre data de livrare a comenzii, produsul v`ndut, cui
i- a fost livrat[ comanda, num[rul de buc[i livrate =i valoarea comenzii.

Figura 8.1
Pentru a u=ura introducerea =i editarea ]nregistr[rilor dintr-o list[ se pot utiliza
facilit[ile oferite de formulare. Un formular reprezint[ o imagine organizat[ a datelor care
cuprinde denumirile coloanelor, casete text pentru introducerea datelor =i butoane pentru
ad[ugarea, =tergerea =i g[sirea ]nregistr[rilor.
Pentru a ad[uga ]nregistr[ri cu ajutorul formularului de date:
1. Se poziioneaz[ cursorul ]n orice celul[ din list[.
2. Din meniul Data se selecteaz[ comanda Form. Pe ecran apare caseta de dialog Data
Form (figura 8.2).
3. Pentru a ad[uga o nou[ ]nregistrare ]n list[ se aplic[ un clic pe butonul New. Pe ecran
apare un formular gol ]n care se completeaz[ fiecare caset[ text cu informaiile
corespunz[toare. Pentru deplasare ]n urm[toarea caset[ se apas[ tasta <Tab>, pentru
deplasare ]n caseta text anterioar[ se apas[ <Shift+Tab>. Dup[ terminarea introducerii

datelor se apas[ tasta <Enter> pentru ad[ugarea de ]nregistr[ri noi ]n list[. }n cazul ]n
care ]n anumite c`mpuri au fost scrise informaii =i se constat[ c[ ]nregistrarea
respectiv[ nu trebuie ad[ugat[ ]n list[, se aplic[ un clic pe butonul Restore pentru a
elimina ]nregistrarea din formular. Clicul pe Restore trebuie aplicat ]nainte de a ap[sa
tasta <Enter > prin care se salveaz[ ]nregistrarea.
4. Se aplic[ un clic pe butonul Close pentru a reveni ]n foaia de calcul.

Figura 8.2
Formularul de date poate fi folosit =i pentru vizualizarea ]nregistr[rilor din list[. Exist[
mai multe metode pentru a realiza acest lucru. O metod[ ar fi folosirea barei de derulare din
caseta de dialog Data Form. Se apas[ pe s[geata ]n sus sau s[geata ]n jos pentru a vizualiza
]nregistrarea anterioar[ sau ]nregistrarea urm[toare. Pe m[sur[ ce sunt vizualizate
]nregistr[rile din list[ ]n colul din dreapta sus al casetei de este indicat numarul curent al
]nregistr[rii. O alt[ metod[ ar fi utilizarea butoanelor Find Next pentru a vizualiza
urm[toarea ]nregistrare =i Find Previous pentru a vedea ]nregistrarea anterioar[. Dac[ la
ap[sarea acestor butoane Excel emite un semnal sonor ]nseamn[ c[ suntei poziionai pe
ultima, respectiv prima ]nregistrare din list[.
Pentru a =terge o ]nregistrare cu ajutorul formularului de date:
2. Din meniul Data se selecteaz[ comanda Form. Pe ecran apare caseta de dialog Data
Form.
3. Se vizualizeaz[ ]nregistrarea care trebuie =tears[.
4. Se aplic[ un clic pe butonul OK pentru a efectua =tergerea. Excel va solicita
confirmarea pentru =tergerea ]nregistr[rii. Se va r[spunde cu OK pentru a =terge
]nregistrarea sau cu Cancel pentru a anula operaia de =tergere.
5. Se aplic[ un clic pe butonul Close pentru revenirea ]n foaia de calcul.
Formularul de date poate fi folosit =i pentru a g[si ]nregistr[rile care satisfac unul sau
mai multe criterii. Dac[ se folose=te formularul ]n acest scop nu se poate vizualiza dec`t c`te
o ]nregistrare g[sit[.
Pa=ii pentru a g[si o ]nregistrare sunt:

Liste
2. Din meniul Data se selecteaz[ comanda Form.
3. Din caseta de dialog Data Form se selecteaz[ butonul Criteria.
4. Se introduc criteriile pentru efectuarea c[ut[rii (figura 8.3). De exemplu, dac[ vrem s[
vizualiz[m comenzile cu o valoare mai mare de 40000000 ]n c`mpul Valoare
Comand[ introducem criteriul
>40000000.

Figura 8.3
5. Se aplic[ un clic pe butonul Find Next sau se apas[ pe s[geata ]n jos din bara de
derulare a formularului. }n formular va fi afi=at rezultatul c[ut[rii.
Dac[ nu exist[ nici o ]nregistrare corespunz[toare se va auzi un semnal sonor.
Dac[ trebuie f[cut[ c[utarea ]n sens invers se aplic[ un clic pe butonul Find Prev sau
se apas[ s[geata ]n sus din bara de derulare a formularului. Dac[ nu exist[ nici o
]nregistrare corespunz[toare se va auzi semnalul sonor.

8.2. Sortarea datelor din liste
Informaiile organizate ]ntr-o list[ pot fi sortate, filtrate sau se pot genera extrase pe
totaluri pariale.
Sortarea este operaia de ordonare a ]nregistr[rilor ]n funcie de unul sau mai multe
criterii. Excel sorteaz[ listele pe baza c`mpurilor.
Pentru a ordona o list[ se efectueaz[ urm[torii pa=i:
1. Se selecteaz[ o celul[ din list[. Dac[ trebuie ordonate doar anumite ]nregistr[ri din
list[, acestea se selecteaz[
2. Se aplic[ comanda Data, Sort. Pe ecran apare caseta de dialog Sort (figura 8.4).
3. Pentru a evita sortarea capului de tabel ]mpreun[ cu restul listei, din seciunea My
List Has se selecteaz[ opiunea Header Row.
4. }n caseta Sort By se selecteaz[ numele coloanei ]n funcie de care se va face sortarea.
Dac[ lista nu conine nume de coloane, =i deci la pasul 3 a fost selectat[ opiunea My
List Has No Header Row, ]n loc de numele coloanei se va selecta litera coloanei din
foaia de calcul.
5. Se selecteaz[ ordinea de sortare: Ascending pentru sortare ]n ordine cresc[toare =i
Descending pentru sortare ]n ordine descresc[toare.

6. Dac[ este necesar[ o sortare pe dou[ nivele (]n cazul ]n care exist[ duplicate ]n
primul c`mp de sortare) se completeaz[ a doua caset[ Then By. Din lista derulant[ se
va selecta numele coloanei ce va fi folosit[ ca al doilea c`mp de sortare. Se selecteaz[
ordinea de sortare pentru al doilea c`mp.
7. Pentru a crea un al treilea nivel de sortare, ]n cazul ]n care exist[ duplicate ]n primele
dou[ c`mpuri de sortare se completeaz[ ]n mod similar a treia caset[ Then By cu al
treilea c`mp de sortare =i se selecteaz[ ordinea de sortare =i pentru acest c`mp.

Figura 8.4 – caseta de dialog Sort
O list[ se poate sorta mai rapid cu ajutorul a dou[ butoane din bara de instrumente
standard: AZ↓, pentru sortare ]n ordine cresc[toare =i ZA↓, pentru sortare ]n ordine
descresc[toare.
Pentru a sorta o list[ cu butoanele de sortare:
1. Se selectez[ o celul[ din coloana ce va fi folosit[ drept cheie de sortare.
2. Se execut[ un clic pe unul din cele dou[ butoane de sortare.
Butoanele de sortare efectueaz[ aceast[ operaie doar dup[ un c`mp cheie - c`mpul
selectat ]nainte de ap[sarea butonului.
Pentru sortare, Excel folose=te urm[toarele reguli:
Datele sunt sortate ]n ordine ascendent[, de la A la Z, de sus ]n jos pentru linii, sau de
la st`nga la dreapta pentru coloane. Opiunea Descending inverseaz[ aceast[ ordine, de la Z
la A, de sus ]n jos sau de la st`nga la dreapta.
• Spaiile libere sunt puse la sf`r=it.
• Este folosit[ urm[toarea ordine de priorit[i:
1.
numerele de la cel mai mic num[r negativ la cel mai mare num[r pozitiv
2.
texte (de la A la Z)
3.
rezultatele FALSE
4.
rezultatele TRUE
5.
valori de eroare
6.
spaii libere

Liste
Excel poate ignora diferenele dintre literele mari =i mici sau poate ine cont de
acestea . Acest lucru se poate specifica dac[ din caseta de dialog Sort se selectez[ butonul
Options. Pe ecran apare caseta de dialog Sort Options (figura 8.5):
Dac[ este marcat[ opiunea Case Sensitive se face distincie ]ntre literele mici =i cele
mari, dac[ nu este marcat[ nu se face distincie. Tot ]n aceast[ caset[ de dialog se specific[ ]n
ce ordine se va face sortarea: - de jos ]n sus (Sort Top To Bottom), sau de la st`nga la
dreapta (Sort Left To Right).

Figura 8.5 - caseta de dialog Sort Options
}n unele cazuri este posibil s[ fie necesar[ o sortare ]n care informaiile nu trebuie s[
apar[ ]n ordine alfabetic[ normal[. }n acest caz din caseta de dialog Sort Options se
selecteaz[ din lista derulant[ First Key Sort Order modul ]n care se va face sortarea dup[
prima cheie.

8.3. Aplicaţie
}n foaia de calcul din lecia precedent[ s[ se grupeze comenzile ]n funcie de ora=ul ]n
care au fost livrate:
Rezolvare:
2. Se selecteaz[ comanda Sort din meniul Data.
3. }n seciunea My List Has se selecteaz[ opiunea Header Row (avem cap de tabel).
4. }n caseta Sort By se selecteaz[ Ora= - numele coloanei dup[ care se face sortarea.
5. Se selecteaz[ opiunea Ascending - vom avea o sortare ]n ordine cresc[toare dup[ numele
ora=elor.
}n cazul ]n care trebuie s[ facem o sortare cu dou[ niveluri de sortare, de exemplu
dup[ ora= =i dup[ produs:
− se repet[ pa=ii 1 - 5, prezentai mai sus (p`n[ acum datele sunt sortate doar dup[ un nivel
de sortare)
6. }n a doua caset[ Then By se selecteaz[ Produs - numele coloanei pentru al doilea criteriu
de sortare. Astfel se specific[ ordinea =i pentru al doilea nivel de sortare.


8.4. Sortarea după mai mult de trei câmpuri
Cu toate c[ ]n caseta de dialog Sort se pot specifica doar trei nivele de sortare,
sortarea se poate face dup[ oric`te c`mpuri. Se poate face o resortare dup[ c`mpuri
suplimentare oric`t de des este necesar, f[r[ a pierde rezultatul ordon[rii sort[rilor
precedente. Regula de sortare dup[ mai mult de trei chei este de a sorta ]nt`i dup[ nivelurile
inferioare merg`nd ]n sus c[tre nivelul superior.
De exemplu, s[ presupunem c[ avem de f[cut o sortare pe 6 nivele ]n care coloana A
este folosit[ ca prim[ cheie de sortare, B ca a doua, C ca a treia, D ca a patra, E ca a cincea =i
F a =asea cheie. De=i Excel permite specificarea doar a trei chei de sortare se pot sorta toate
cele =ase coloane.
Se sorteaz[ mai ]nt`i coloanele de nivel inferior: D, E ,F. Coloana D va fi prima cheie
de sortare, E a doua, F a treia. O a doua sortare efectueaz[ operaia dup[ coloanele de nivel
superior A, B, C. Coloana A va fi prima cheie de sortare, B a doua =i C a treia.

Prelucrarea datelor cu ajutorul subtotalurilor

CAPITOLUL 9
PRELUCRAREA DATELOR CU AJUTORUL SUBTOTALURILOR
9.1. Crearea subtotalurilor automate
C`nd sorteaz[ datele dintr-o list[, Excel permite efectuarea unor sinteze a datelor pe
baza totalurilor pariale. C`nd se efectueaz[ calcule pariale, acestea sunt calculate pentru
fiecare grup din list[. Un grup este alc[tuit din mai multe linii (]nregistr[ri) care au aceea=i
informaie ]ntr-o coloan[ (c`mp) specificat[.
Pentru a putea crea subtotaluri trebuie ca datele s[ fie sortate. Dup[ sortarea datelor
dup[ c`mpuri, se parcurg urm[torii pa=i:
1. Se selecteaz[ orice celul[ din list[.
2. Se aplic[ comanda Data, Subtotals. Pe ecran apare caseta de dialog Subtotal (figura
9..1).

Figura 9..1 – caseta de dialog Subtotal
3. Se specific[ modul ]n care vor fi grupate datele pentru subtotaluri select`nd din lista
derulant[ At Each Change(la fiecare schimbare) numele coloanei dup[ care se face
gruparea.
Dac[ este prima dat[ c`nd este selectat[ comanda, Excel selecteaz[ automat coloana cea
mai din st`nga. Dac[ comanda a fost folosit[ =i mai ]nainte, atunci va fi selectat[ coloana
folosit[ ultima dat[.
4. Din lista derulant[ Use Function se selecteaz[ funcia care trebuie calculat[. Funciile cel
mai frecvent folosite sunt:
SUM – adunare
MAX – maximum
MIN – minimum
AVERAGE – medie
PRODUCT – produs
VAR - variana
STD DEVP - deviaia standard;

Modelarea deciziilor utilizeând foile de calcul
5. Din lista Add Subtotal To se selecteaz[ datele cu care se vor efectua calculele. Aceast[
list[ conine numele coloanelor din lista de date. Se marcheaz[ coloanele pentru care se
vor efectua calculele.
6. Pentru a ]nlocui totaluri existente se marcheaz[ opiunea Replace Current Subtotals.
7. Pentru a insera un salt de pagin[ ]naintea fiec[rui grup se marcheaz[ opiunea Page
Break Between Groups.
8. }n mod implicit subtotalurile =i totalurile generale apar la sf`r=itul grupului de date
(opiunea Summary Below Data se marcheaz[ automat). Dac[ ele trebuie afi=ate ]naintea
grupului de date se va demarca opiunea Summary Below Data.
Pentru eliminarea subtotalurilor din caseta de dialog Subtotal se selecteaz[ butonul
Remove All.

9.2. Aplicaţie
La datele din aplicaia din lecia 8 s[ se calculeze valoarea total[ a comenzilor livrate
]n fiecare ora=.
1. Se sorteaz[ comenzile dup[ ora=.
3. Din meniul Data se aplic[ comanda Subtotals.
4. Caseta de dialog Subtotal se va completa ]n modul urm[tor (figura 9..2):
Din lista At Each Change se selcteaz[ Ora=. Se va genera c`te un grup de ]nregist[ri
pentru fiecare ora=. Din lista Use Function se va selecta funcia SUM, iar ]n lista Add
Subtotal To se va marca coloana Valoare comand[. Deci pentru fiecare grup se va
calcula suma valorilor din coloana Valoare comand[.
Se marcheaz[ opiunile Replace Current Subtotals =i Summary Below Data.

Figura 9..2
Excel insereaz[ r`ndurile de subtotal pentru fiecare grup =i realizeaz[ calculul
specificat ]n coloanele alese. Excel eticheteaz[ fiecare r`nd inserat cu un titlu potrivit. Se
insereaz[ de asemenea un r`nd de total general.

C`nd se adaug[ totaluri pariale calculate automat ]ntr-o list[, Excel afi=eaz[ lista ]n
modul Outline. Nivelul detaliilor din list[ poate fi extins sau restr`ns pentru a nu fi afi=ate
dec`t totalurile pariale =i totalurile generale pentru datele respective. }n partea st`ng[ a
ferestrei (figura 9..3) apar c`teva butoane care permit ascunderea =i afi=area rapid[ a datelor
de detaliu:
• (-) Hide Detail - pentru a condensa sintetizarea datelor - apare ]n dreptul fiec[rui
subtotal calculat
• (+) Display Detail - pentru a extinde sintetizarea datelor - apare ]n dreptul fiec[rui
subtotal calculat
• 1, 2, 3, ... - butoane de ierarhizare care indic[ modul cum sunt grupate datele.
}n exemplul prezentat, deoarece s-a efectuat o grupare pe un nivel, sunt afi=ate doar
trei butoane: 1, 2 =i 3. Dac[ se apas[ pe butonul 1 este afi=at doar totalul general (figura 9.4),
dac[ se apas[ pe butoanul 2 sunt afi=ate totalurile pariale, iar dac[ se apasa butonul 3 este
vizualizat[ toat[ lista.
Pentru a ascunde un nivel de detaliere se selecteaz[ o celul[ care conine un total
parial =i se aplic[ un clic pe butonul Hide Detail Level (-) de pe nivelul 2. Excel va reduce
dimensiunile listei astfel ]nc`t este afi=at doar r`ndul care conine totalul parial
corespunz[tor. Dac[ se aplic[ un clic pe butonul Display Detail (+) vor fi afi=ate toate
]nregistr[rile pe baza c[rora s-a calculat subtotalul corespunz[tor.
Butoanele Hide Detail (-) =i Display Detail (+) de pe nivelul 1 sunt folosite pentru
a condensa sau extinde datele care genereaz[ totalul general.

Figura 9..3

Modelarea deciziilor utilizeând foile de calcul

Figura 9..4

9.3. Crearea de subtotaluri ierarhizate
Dac[ ]n cadrul unui grup trebuie calculate subtotaluri suplimentare se vor calcula
subtotaluri ierarhizate.
Pentru a crea un subtotal ierarhizat datele trebuie sortate =i dup[ a doua cheie. Apoi se
aplic[ comanda Data, Subtotals. Se vor selecta opiunile pentru grupul principal (cel mai
mare). Excel insereaz[ subtotalurile pentru primul grup.
Se alege ]n continuare Data, Subtotals =i opiunile pentru urm[toarele subseturi de
grupe. Opiunea Replace Current Subtotals trebuie s[ fie demarcat[. Excel insereaz[ c`te
un subtotal pentru urm[toarele subseturi de grupuri.

9.4. Aplicaţie
Pe l`ng[ subtotalurile pe ora=e =i totalul general se mai pot calcula =i subtotaluri pe
produse. Pentru a realiza acest lucru:
1. Se face o sortare a listei pe dou[ niveluri: nivelul 1 - sortare dup[ ora=; nivelul 2 sortare dup[ produs.
2. Ca ]n aplicaia precedent[ se calculeaz[ subtotalurile pe ora=.


Figura 9..5
3. Se aplic[ din nou comanda Data, Subtotals. Caseta de dialog Subtotal se
completeaz[ ]n modul urm[tor:
Din lista At Each Change In se selecteaz[ c`mpul Produs (se vor genera subgrupe
pentru fiecare produs).
Din lista Use Function se selecteaz[ funcia SUM, iar ]n lista Add Subtotal To se
marcheaz[ c`mpul Valoare comand[ (se calculeaz[ suma valorilor comenzilor
pentru fiecare subgrup).
Se demarcheaz[ opiunea Replace Current Subtotals.
Se obine rezultatul din figura 9.5.
}n colul din st`nga sus a ferestrei apar butoanele de ierarhizare 1, 2, 3, 4. Acum apar
mai multe butoane de ierarhizare pentru c[ se calculeaz[ subtotalurile pentru mai multe
nivele (produs =i ora=). Pentru a afi=a doar totalul general se aplic[ un clic pe butonul de nivel
1. Dac[ trebuie afi=ate doar totalurile v`nz[rilor efectuate ]n fiecare ora= =i totalul general se
aplic[ un clic pe butonul de nivel 2. Dac[ trebuie afi=ate subtotalurile pe produs =i ora= se
aplic[ un clic pe butonul 3, iar dac[ trebuie afi=at[ toat[ lista se aplic[ un clic pe butonul 4.

Excel curs-1

More Related Content

What's hot

Viewers also liked

Similar to Excel curs-1

More from zfrunzescu

Excel curs-1