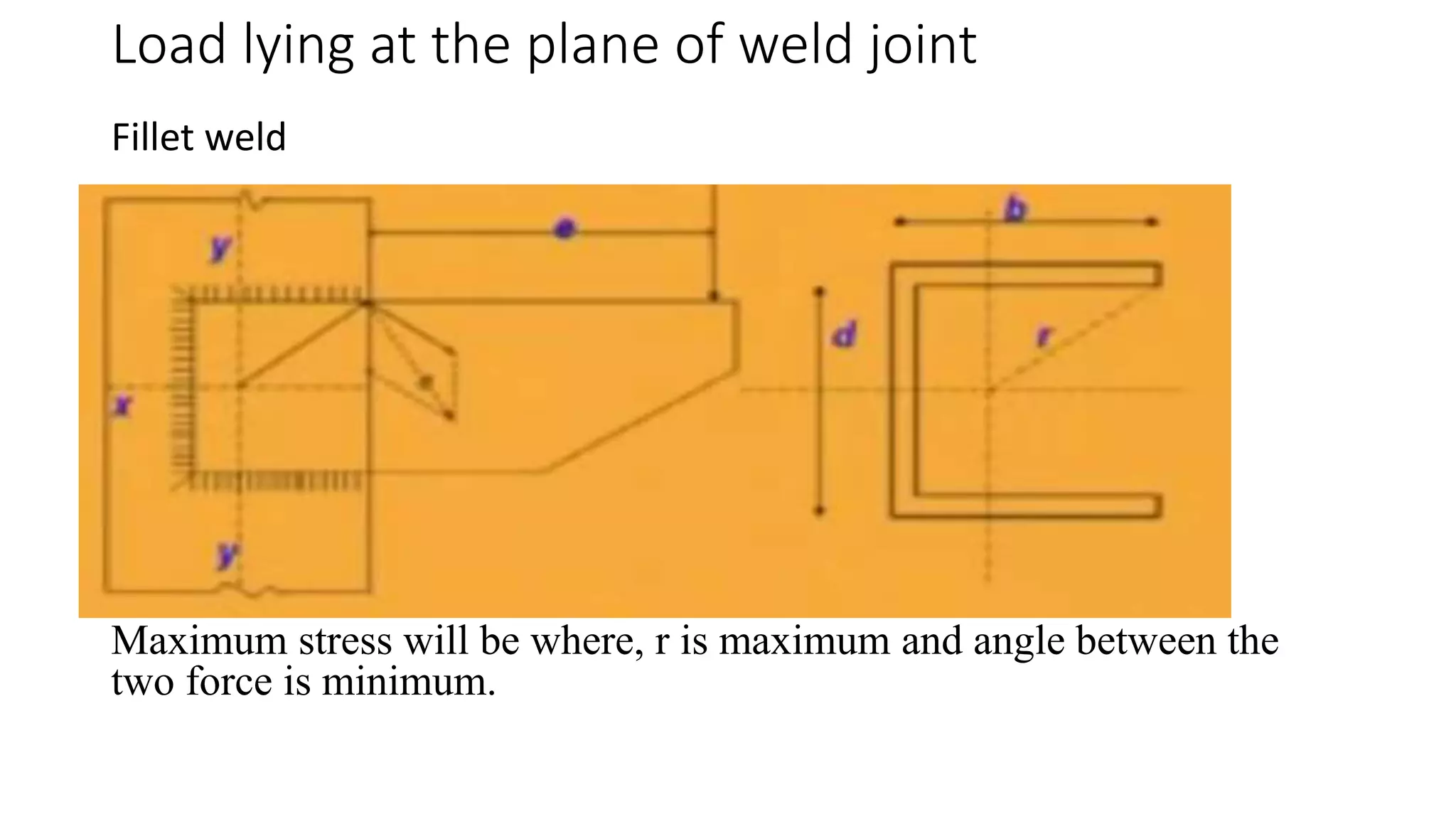
1) Eccentric connections experience both direct axial forces and bending moments due to eccentric loads. This results in more complex stress distributions compared to concentric connections. 2) For bracket connections with eccentric loads, the direct shear stress and bending stress due to the moment must be calculated and combined using the Pythagorean theorem. 3) For welded joints with eccentric loads, both the direct shear stress and bending stress in the weld must be determined and combined, considering the weld geometry, load magnitude and eccentricity. The resultant stress must satisfy allowable stress criteria.

1. Eccentric connections
by: Dinesh Nath

2. Eccentric connections
• If the force applied does not passes through the CG of the joint then
such joint carries moment in addition to an axial direct force. Such
types of connections are called as eccentric connections

5. Bracket connection
• If load is P then a moment P x e acting at the CG of the bolt/rivet
group.
• Then direct shear due to axial load P = Fs =
𝑃
𝑛
and Fs always acts
downward in vertical direction.
• Now shear due to moment (P x e) will be calculated by using
Fm =
𝑀𝑟
𝝨𝑟2 =
𝑃𝑒𝑟
𝝨𝑟2
The resultant of Fs and Fm act on the bolt. If 𝝷 is the angle between Fs
and Fm then the resultant F = Fs
2+Fm
2 + 2FsFm 𝑐𝑜𝑠𝝷

6. Examples
• A bracket connection with 8 rivets of 20 mm diameter. Rivets are
placed such a way that pitch and edge distance are 50 mm. The gauge
distance is 60 mm. It is carrying a eccentric load of 220 kN with 250
mm eccentricity. Analyse the Joint.

7. • A load is inclined at 45o with the bracket as shown in the figure in
below 5-20mm diameter rivets are used and plates connected are 12
mm thick. Find the maximum amount of load which can carry by the
joint. Assume Allowable shear stress and bearing stress as 100 and 300
Mpa respectively.

8. • If the magnitude of load is high but moment is low then n = P/R &
increases the value of n by further 25%
• If the magnitude of moment is high & direct load is less then
• n = 6𝑀/𝑚𝑅𝑝

9. Eccentric joints
1) Load lying at the plane of weld joint
2) Load lying perpendicular to the plane of weld joint
a) Fillet weld
b) Butt weld

10. Load lying at the plane of weld joint
Fillet weld
Maximum stress will be where, r is maximum and angle between the
two force is minimum.

11. • Let us consider a weld of size = s
• Throat thickness t = 0.707s
• Direct stress in the weld Pe =
𝑃
𝐿𝑡
• Stress due to torsional moment = Pb =
𝑀
𝐼 𝑝
r
Where p = total vertical load
e = eccentricity
L = total length of the weld = 2b + d
M = Moment = Pe
r = Radial distance of the welding point from the CG of the weld
Ip = Polar moment of Inertia of the weld = Ixx + Iyy

12. At any point resultant stress is given by P = Pe
2+𝑃 𝑏
2 + 2PePb 𝑐𝑜𝑠𝝷
For critical condition P < 108 MPa.
Example:
A bracket is subjected to a load of 90kN and connected to a stanchion
by welding. Find the size of the weld so that load can be carried safely,

13. Load lying perpendicular to the plane of weld
joint:
a) fillet weld
b) Butt weld
Let
t – Throat thickness
d – Welding depth/ length
P – Total vertical load
e – Eccentricity
Total length of the well = 2d

14. • Direct shear stress in the weld, pt =
𝑃
2𝑑𝑡
• Stress due to bending Pb =
𝑀
𝐼
𝑦 =
3𝑃𝑒
𝑡𝑑2
• Resultant stress = Pr = Pt
2+𝑃 𝑏
2
• Check: Pr < 108 MPa.
Example: Design a fillet weld to connect a 10mm thick bracket to the
flange of a column as shown in the figure below.

15. • A steel pipe is subjected to a vertical load with an eccentricity of 400
mm from the welded and as shown in figure. The pipe is connected to
a rectangular plate of 10 mm thickness by fillet weld around the
perimeter. Torsional moment of 6kN-m is acting on the pipe. Inner
radius of pipe is 80mm and outer is 100mm. Assuming the size of the
weld is 8mm find the allowable load on the pipe.