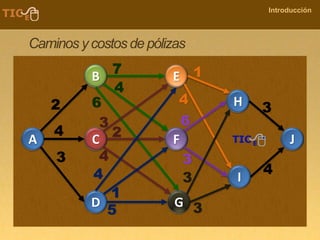
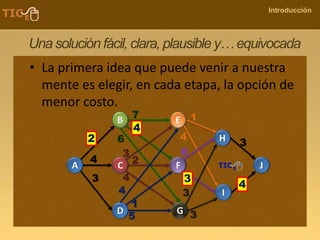
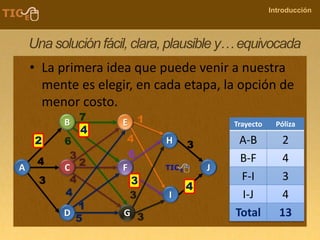
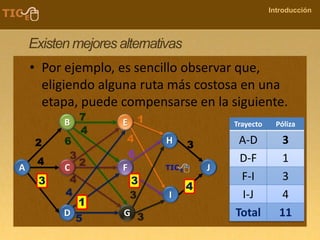
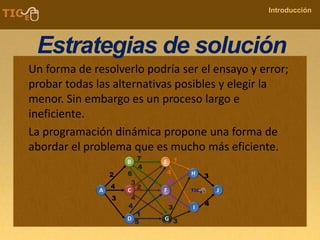
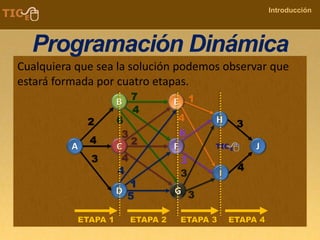
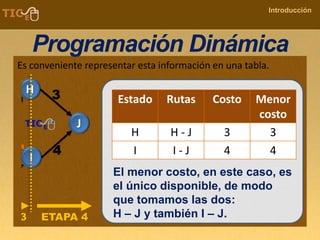
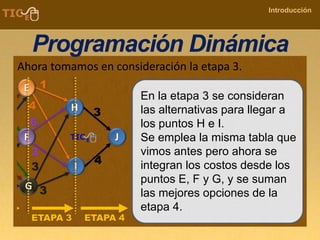
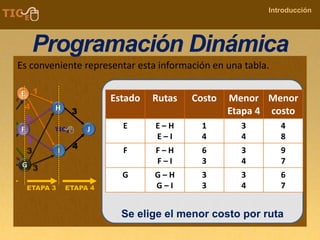
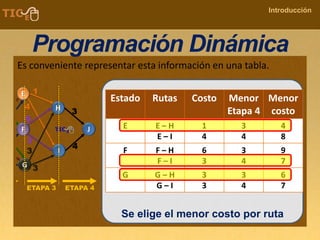
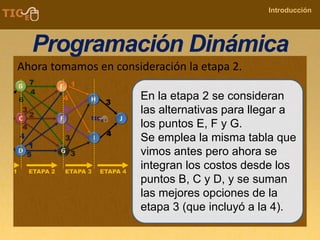
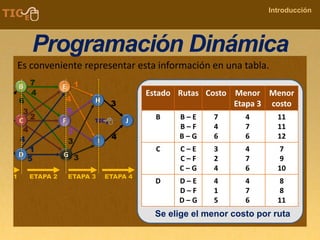
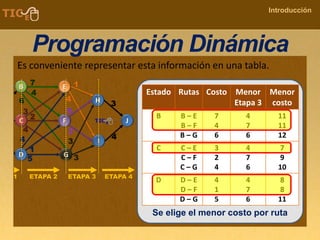
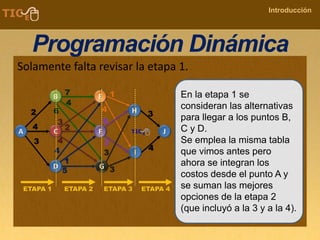
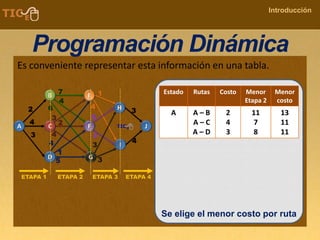
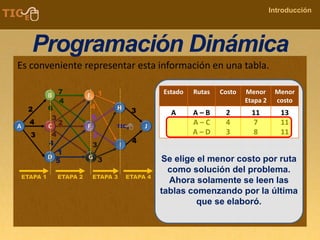
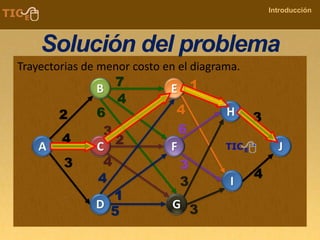
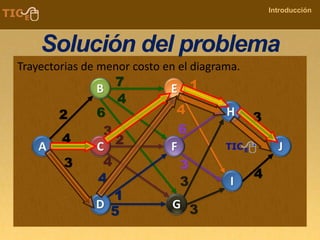
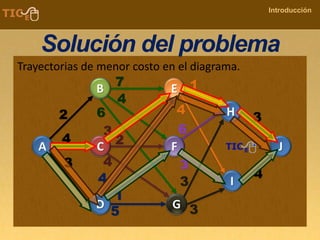
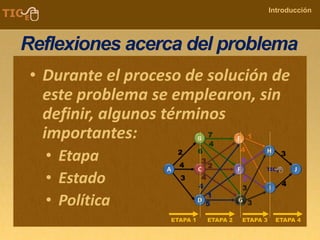
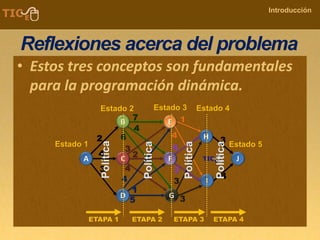
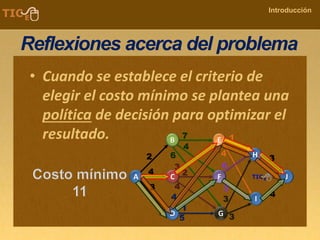
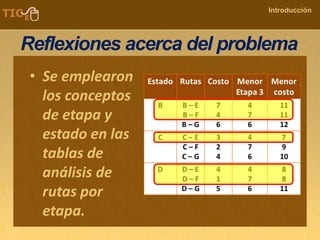
La programación dinámica es una técnica matemática utilizada para tomar decisiones secuenciales interrelacionadas, que optimiza un resultado sin seguir un algoritmo estándar. Se presenta a través del 'problema de la diligencia', donde un viajero busca la ruta más segura y económica en un viaje, ejemplificando cómo seleccionar la mejor opción entre alternativas. Este método se basa en dividir el problema en etapas, definir políticas de decisión y analizar estados, resultando en una solución óptima que puede aplicarse a diversos problemas.

1. COMPANY NAME
Introducción
Programación
Dinámica
G. Edgar Mata Ortiz
“Para todo problema humano hay siempre una
solución fácil, clara, plausible y… equivocada”
Henry-Louis Mencken (1880-1956)

2. COMPANY NAME
Introducción
Contenido
• ¿Qué es la programación
dinámica?
• Características de la programación
dinámica (PD)
• Ejemplo 1
• Reflexión

3. COMPANY NAME
Introducción
¿Quées la programación dinámica?
• Es una técnica matemática que se aplica en
la toma de decisiones secuenciales
interrelacionadas.
• Proporciona un procedimiento, pero no un
algoritmo, para determinar la combinación
de decisiones que optimiza un resultado.

4. COMPANY NAME
Introducción
Características de la programación dinámica
• A diferencia de la programación lineal no
existe una formulación matemática
estándar.
• Es una estrategia general cuyas ecuaciones
se ajustan a cada situación particular
• No existe “el problema” de la programación
dinámica
• Requiere de creatividad para su aplicación
𝒚 = 𝒇(𝒙)

5. COMPANY NAME
Introducción
Ejemplo
• El problema de la
diligencia.
• Es un problema
artificial diseñado para
explicar el concepto de
la PD.
• Permite introducir la
terminología de la PD
en forma clara y
comprensible

6. COMPANY NAME
Introducción
EL PROBLEMA
DE LA
DILIGENCIA
Tomado del libro:
Introducción a la Investigación
de Operaciones
Novena edición
Frederick S. Hillier
Gerald J. Lieberman

7. COMPANY NAME
Introducción
Síntesis de la redacción del problema
• Un aventurero desea viajar en diligencia
desde Missouri hasta California a mediados
del siglo XIX.
• Es un viaje peligroso y, aunque su origen y
destino son fijos, tiene muchas opciones en
cuanto a que estados, ciudades o pueblos
elegir como etapas intermedias de su viaje.

8. COMPANY NAME
Introducción
Síntesis de la redacción del problema
• Este viajero ha ideado una manera bastante
ingeniosa para determinar la ruta más
segura.
• Dado que están disponibles seguros de vida
para el viajero, seguramente la ruta con
menos riesgo será aquella cuya póliza por el
recorrido total sea más barata.

9. COMPANY NAME
Introducción
¿Cuál es la ruta de menor costo?
Esta es la pregunta que trataremos de contestar, y
servirá para introducir el vocabulario y conceptos de
la programación dinámica.

10. COMPANY NAME
Introducción
Caminos y costos de pólizas
A C
B
D
E
F
G
H
I
J
2
4
3
7
4
6
3
2
4
4
1
5
4
1
6
3
3
3
3
4

11. COMPANY NAME
Introducción
Una solución fácil, clara, plausible y…equivocada
• La primera idea que puede venir a nuestra
mente es elegir, en cada etapa, la opción de
menor costo.
2
4
3
4

12. COMPANY NAME
Introducción
Una solución fácil, clara, plausible y…equivocada
• La primera idea que puede venir a nuestra
mente es elegir, en cada etapa, la opción de
menor costo.
2
4
3
4
Trayecto Póliza
A-B 2
B-F 4
F-I 3
I-J 4
Total 13

13. COMPANY NAME
Introducción
Existen mejores alternativas
• Por ejemplo, es sencillo observar que,
eligiendo alguna ruta más costosa en una
etapa, puede compensarse en la siguiente.
3
1
3
4
Trayecto Póliza
A-D 3
D-F 1
F-I 3
I-J 4
Total 11

14. COMPANY NAME
Introducción
Estrategias de solución
Un forma de resolverlo podría ser el ensayo y error;
probar todas las alternativas posibles y elegir la
menor. Sin embargo es un proceso largo e
ineficiente.
La programación dinámica propone una forma de
abordar el problema que es mucho más eficiente.

15. COMPANY NAME
Introducción
Programación Dinámica
Cualquiera que sea la solución podemos observar que
estará formada por cuatro etapas.
ETAPA 1 ETAPA 2 ETAPA 3 ETAPA 4

16. COMPANY NAME
Introducción
Programación Dinámica
El análisis comienza en la etapa 4.
En la etapa cuatro solamente existen
dos rutas:
Desde H hasta J
Desde I hasta J
Cada una de ellas tiene diferente
costo, pero no existen alternativas
en cada caso, sólo existe una ruta:
Desde H hasta J, costo = 3
Desde I hasta J, costo = 4

17. COMPANY NAME
Introducción
Programación Dinámica
Es conveniente representar esta información en una tabla.
Estado Rutas Costo Menor
costo
H H - J 3 3
I I - J 4 4
El menor costo, en este caso, es
el único disponible, de modo
que tomamos las dos:
H – J y también I – J.

18. COMPANY NAME
Introducción
Programación Dinámica
Ahora tomamos en consideración la etapa 3.
En la etapa 3 se consideran
las alternativas para llegar a
los puntos H e I.
Se emplea la misma tabla que
vimos antes pero ahora se
integran los costos desde los
puntos E, F y G, y se suman
las mejores opciones de la
etapa 4.

19. COMPANY NAME
Introducción
Programación Dinámica
Es conveniente representar esta información en una tabla.
Estado Rutas Costo Menor
Etapa 4
Menor
costo
E E – H
E – I
1
4
3
4
4
8
F F – H
F – I
6
3
3
4
9
7
G G – H
G – I
3
3
3
4
6
7
Se elige el menor costo por ruta

20. COMPANY NAME
Introducción
Programación Dinámica
Es conveniente representar esta información en una tabla.
Estado Rutas Costo Menor
Etapa 4
Menor
costo
E E – H
E – I
1
4
3
4
4
8
F F – H
F – I
6
3
3
4
9
7
G G – H
G – I
3
3
3
4
6
7
Se elige el menor costo por ruta

21. COMPANY NAME
Introducción
Programación Dinámica
Ahora tomamos en consideración la etapa 2.
En la etapa 2 se consideran
las alternativas para llegar a
los puntos E, F y G.
Se emplea la misma tabla que
vimos antes pero ahora se
integran los costos desde los
puntos B, C y D, y se suman
las mejores opciones de la
etapa 3 (que incluyó a la 4).

22. COMPANY NAME
Introducción
Programación Dinámica
Es conveniente representar esta información en una tabla.
Estado Rutas Costo Menor
Etapa 3
Menor
costo
B B – E
B – F
B – G
7
4
6
4
7
6
11
11
12
C C – E
C – F
C – G
3
2
4
4
7
6
7
9
10
D D – E
D – F
D – G
4
1
5
4
7
6
8
8
11
Se elige el menor costo por ruta

23. COMPANY NAME
Introducción
Programación Dinámica
Es conveniente representar esta información en una tabla.
Estado Rutas Costo Menor
Etapa 3
Menor
costo
B B – E
B – F
B – G
7
4
6
4
7
6
11
11
12
C C – E
C – F
C – G
3
2
4
4
7
6
7
9
10
D D – E
D – F
D – G
4
1
5
4
7
6
8
8
11
Se elige el menor costo por ruta

24. COMPANY NAME
Introducción
Programación Dinámica
Solamente falta revisar la etapa 1.
En la etapa 1 se
consideran las alternativas
para llegar a los puntos B,
C y D.
Se emplea la misma tabla
que vimos antes pero
ahora se integran los
costos desde el punto A y
se suman las mejores
opciones de la etapa 2
(que incluyó a la 3 y a la 4).

25. COMPANY NAME
Introducción
Programación Dinámica
Es conveniente representar esta información en una tabla.
Estado Rutas Costo Menor
Etapa 2
Menor
costo
A A – B
A – C
A – D
2
4
3
11
7
8
13
11
11
Se elige el menor costo por ruta

26. COMPANY NAME
Introducción
Programación Dinámica
Es conveniente representar esta información en una tabla.
Estado Rutas Costo Menor
Etapa 2
Menor
costo
A A – B
A – C
A – D
2
4
3
11
7
8
13
11
11
Se elige el menor costo por ruta
como solución del problema.
Ahora solamente se leen las
tablas comenzando por la última
que se elaboró.

27. COMPANY NAME
Introducción
Análisis de las tablas
• La tabla final indica que debemos elegir cualquiera
de dos rutas:
• De A hacia C con un costo total de 11
• De A hacia D con el mismo costo total de 11
• Se descarta la ruta de A hacia B porque, en el
mejor de los casos, se logra un costo de 13.

28. COMPANY NAME
Introducción
Análisis de las tablas
• En la penúltima tabla
(etapa 2) tomamos
solamente las
opciones de C y D con
menor costo porque ya
determinamos que
cualquier ruta que
inicia con A-B es más
costosa.
Rutas de menor costo:
A – C – E
A – D – E
A – D – F

29. COMPANY NAME
Introducción
Análisis de las tablas
• En la segunda tabla
(etapa 3) tomamos
solamente las
opciones E y F debido
a que la ruta que
pasa por G fue
eliminada en el paso
anterior.
Rutas de menor costo:
A – C – E – H
A – D – E – H
A – D – F – I

30. COMPANY NAME
Introducción
Análisis de las tablas
• En la primera tabla
(etapa 4) tomamos
solamente las
opciones H e I debido
a que no existen
alternativas.
Rutas de menor costo:
A – C – E – H – J (Costo = 11)
A – D – E – H – J (Costo = 11)
A – D – F – I – J (Costo = 11)

31. COMPANY NAME
Introducción
Solución del problema
Trayectorias de menor costo en el diagrama.

32. COMPANY NAME
Introducción
Solución del problema
Trayectorias de menor costo en el diagrama.

33. COMPANY NAME
Introducción
Solución del problema
Trayectorias de menor costo en el diagrama.

34. COMPANY NAME
Introducción
Reflexiones acerca del problema
• Durante el proceso de solución de
este problema se emplearon, sin
definir, algunos términos
importantes:
• Etapa
• Estado
• Política

35. COMPANY NAME
Introducción
Reflexiones acerca del problema
• Estos tres conceptos son fundamentales
para la programación dinámica.

36. COMPANY NAME
Introducción
Reflexiones acerca del problema
• Estos tres conceptos son fundamentales
para la programación dinámica.
Estado 1
Estado 2 Estado 3 Estado 4
Estado 5

37. COMPANY NAME
Introducción
Reflexiones acerca del problema
• Estos tres conceptos son fundamentales
para la programación dinámica.
Estado 1
Estado 2 Estado 3 Estado 4
Estado 5
Política
Política
Política
Política

38. COMPANY NAME
Introducción
Reflexiones acerca del problema
• Cuando se establece el criterio de
elegir el costo mínimo se plantea una
política de decisión para optimizar el
resultado.

39. COMPANY NAME
Introducción
Reflexiones acerca del problema
• Se emplearon
los conceptos
de etapa y
estado en las
tablas de
análisis de
rutas por
etapa.

40. COMPANY NAME
Introducción
Características de un problema de PD
1. El problema se puede dividir
en etapas.
2. Cada etapa requiere de una
política de decisión
EL problema está formado
por una serie de decisiones
interrelacionadas.

41. COMPANY NAME
Introducción
Características de un problema de PD
3. Cada etapa tiene cierto número de
estados asociados con su inicio
Los estados pueden verse como
condiciones posibles en las que se
puede encontrar el sistema en cada
etapa del problema

42. COMPANY NAME
Introducción
Características de un problema de PD
4. El efecto de la política de decisión es
transformar el estado actual en un
estado asociado con el inicio de la
siguiente etapa.
Los problemas de PD pueden
interpretarse en términos de redes, la
solución consiste en encontrar la
trayectoria más corta o más larga.

43. COMPANY NAME
Introducción
Características de un problema de PD
5. El procedimiento de solución está
diseñado para encontrar una política
óptima para manejar el problema
completo.
En cualquier problema, la PD
proporciona, no solamente la solución
óptima, sino una política de decisión
aplicable a cualquier circunstancia.

44. COMPANY NAME
Introducción
Características de un problema de PD
6. Principio de optimalidad de la PD.
Dado el estado actual, una política
óptima para las etapas restantes es
independiente de la política adoptada
en las etapas anteriores.

45. COMPANY NAME
Introducción
GRACIAS POR SUATENCIÓN
Fuentes de información en línea:
http://licmata-math.blogspot.mx/
http://www.scoop.it/t/mathematics-learning
https://www.facebook.com/licemata
https://www.linkedin.com/in/licmata
Twitter @licemata