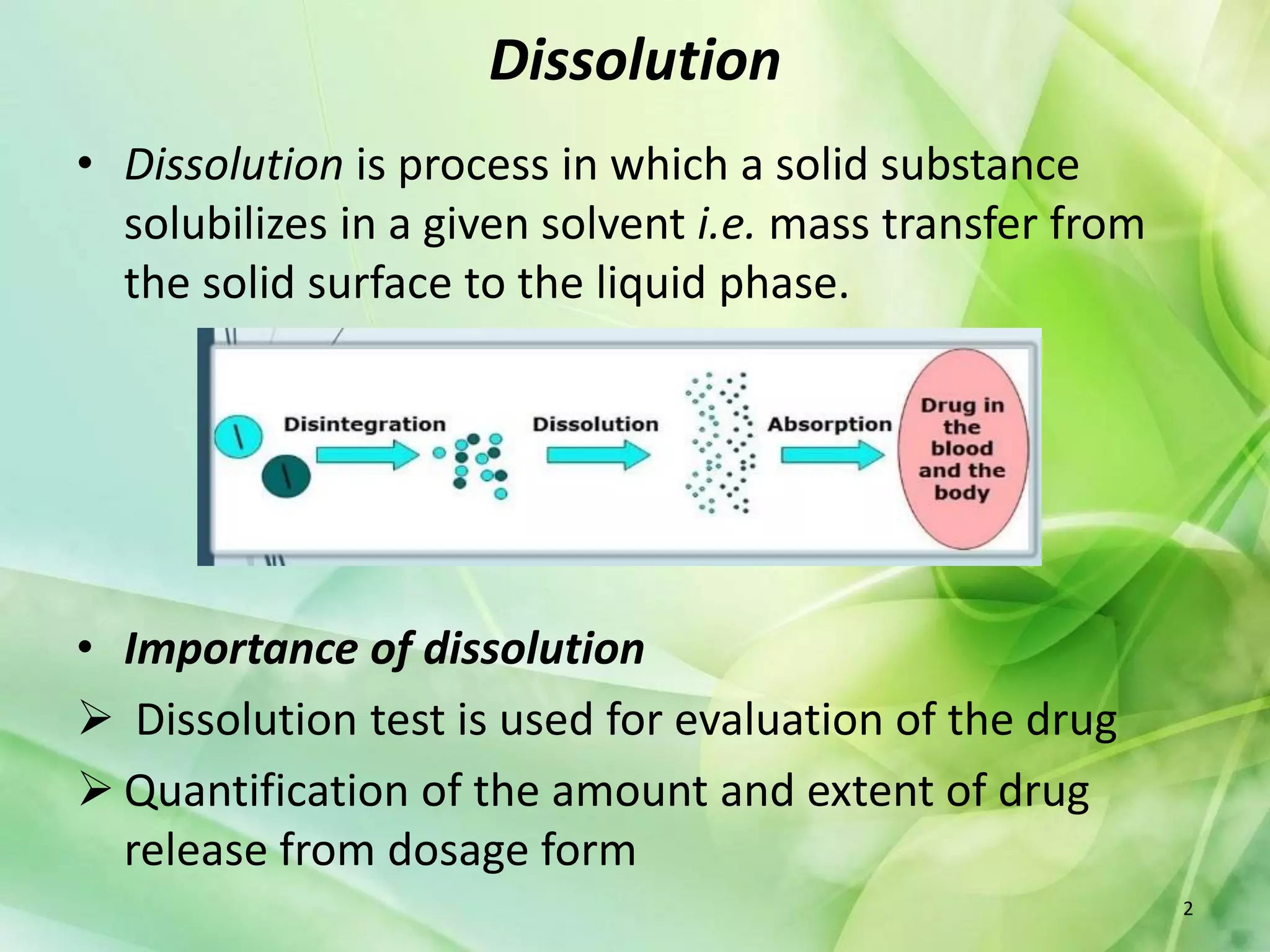
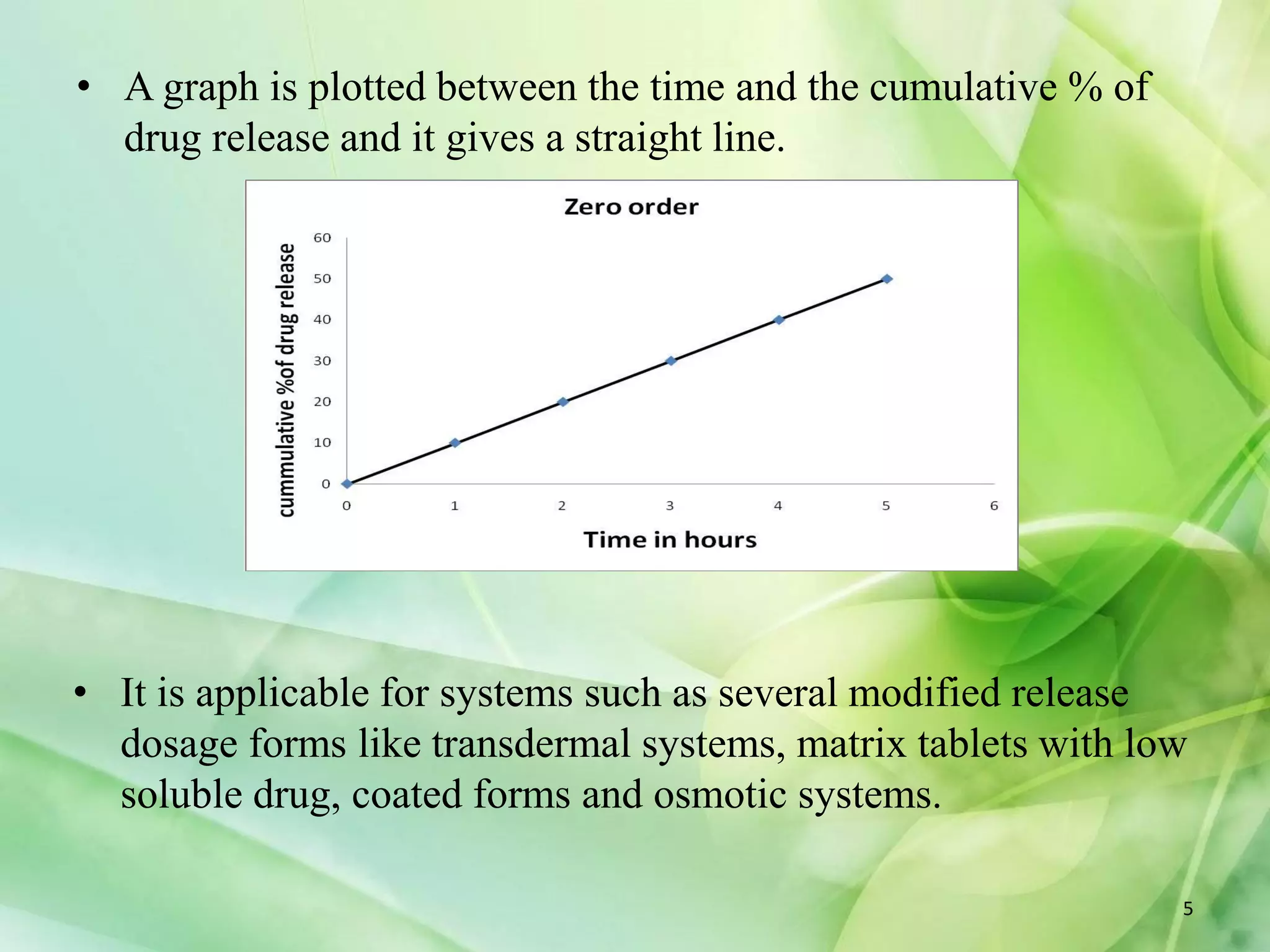
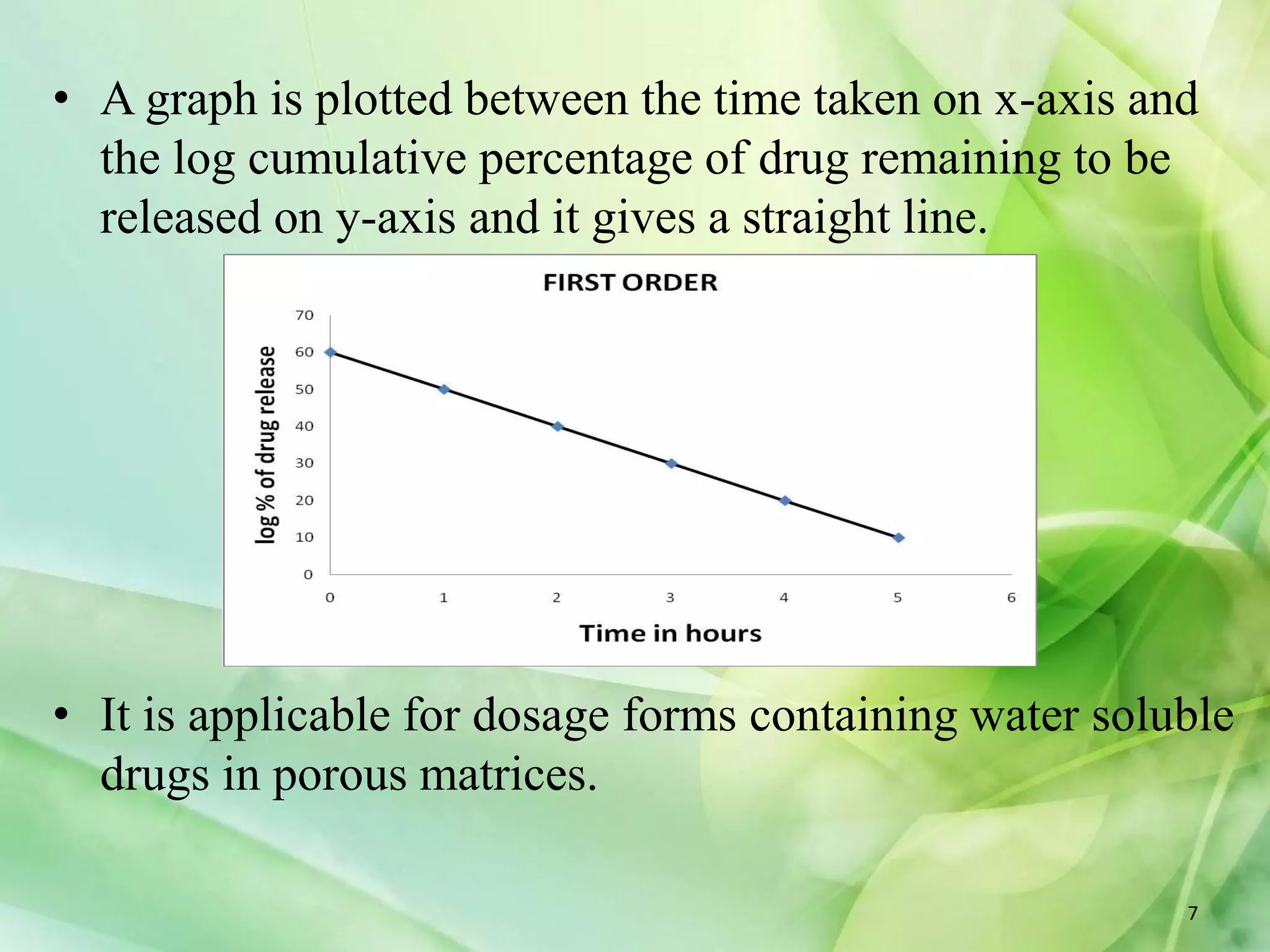
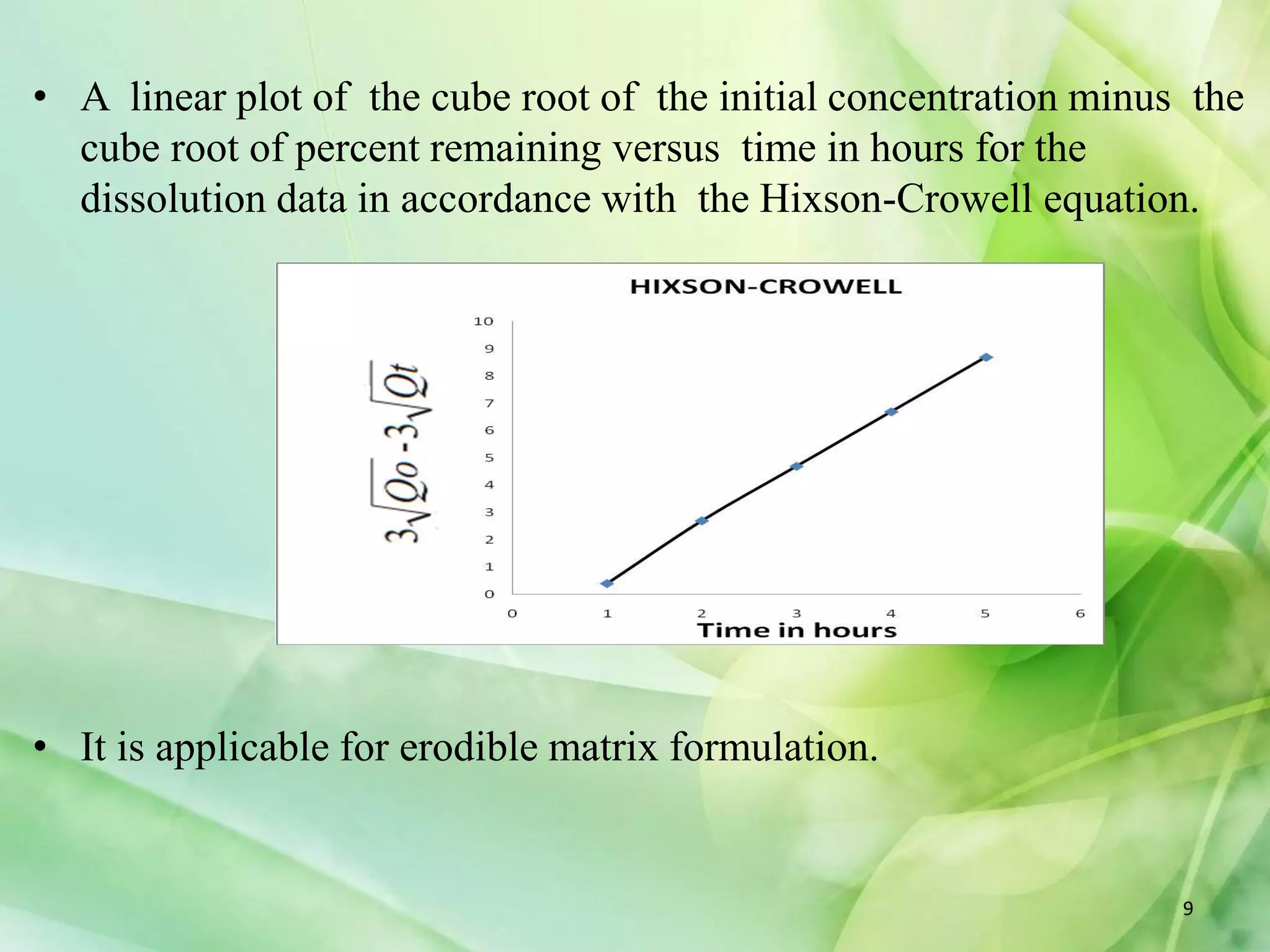
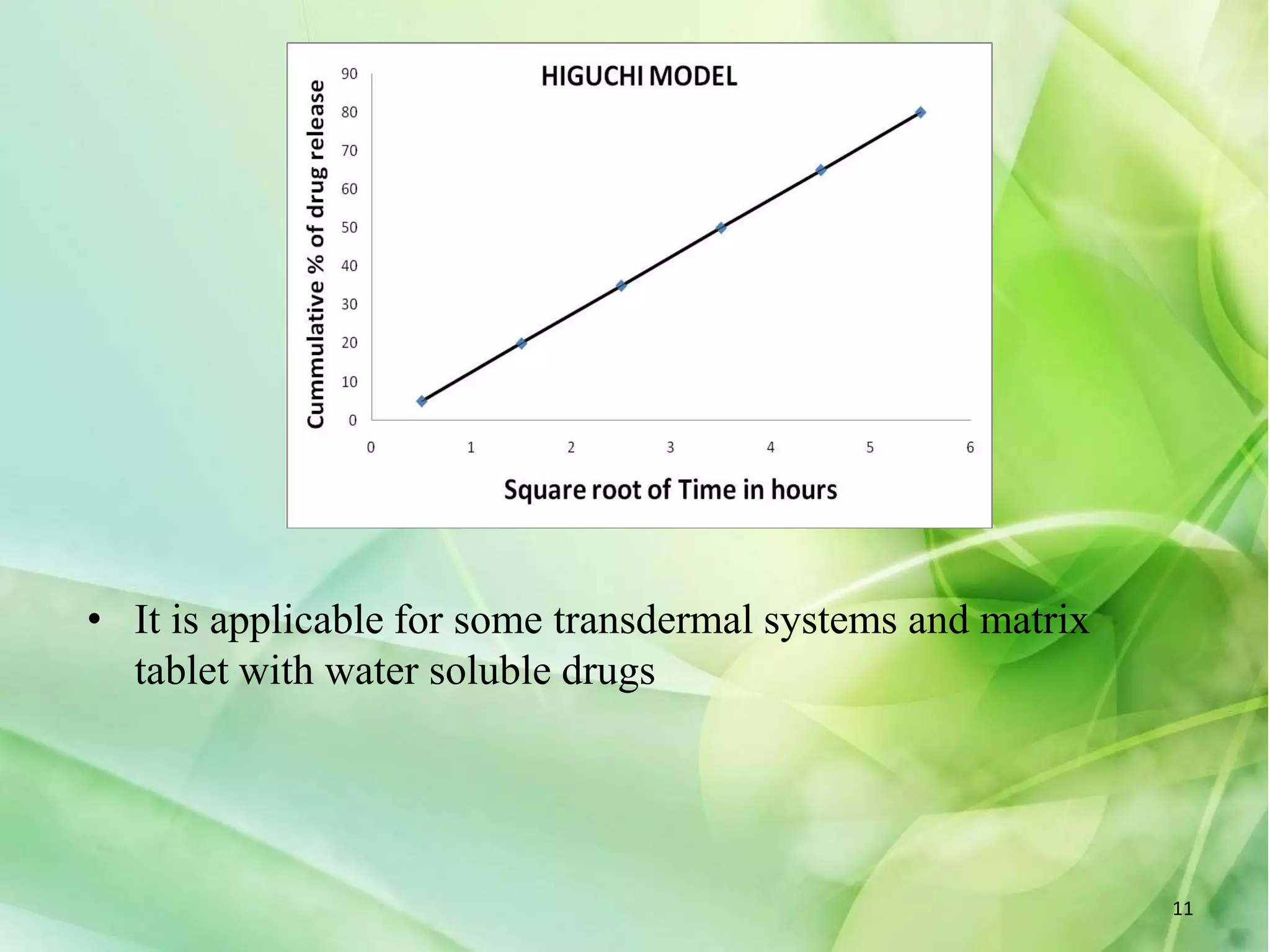
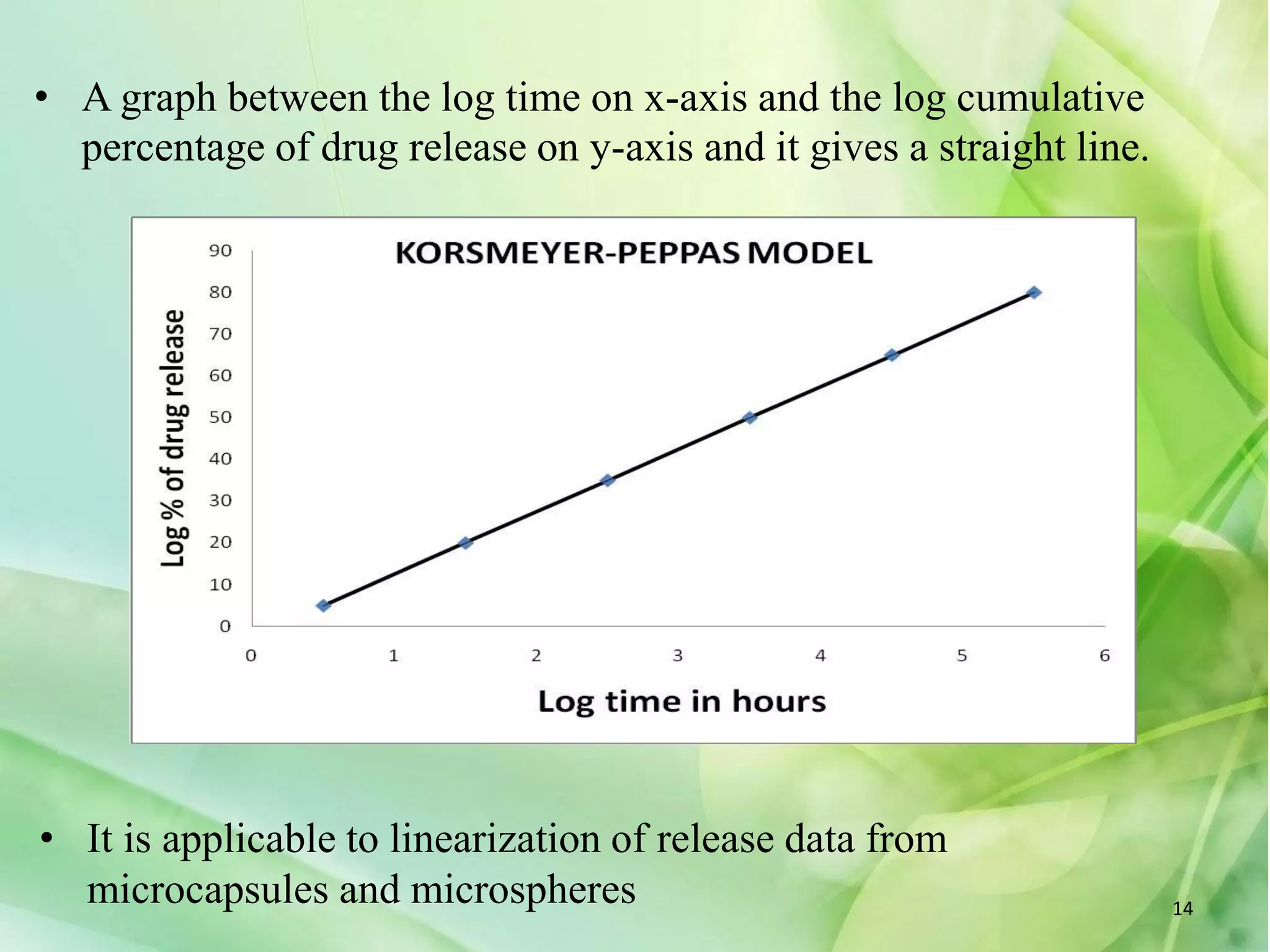
This document discusses various mathematical models that can be used to determine the kinetics of drug release from pharmaceutical dosage forms, including zero-order, first-order, Hixon-Crowell, Higuchi, Korsemeyer-Peppas, and Weibull models. It provides the key equations for each model and describes scenarios in which each model is applicable, such as matrix tablets, coated forms, transdermal systems, and others. The models can be used to analyze drug dissolution data and understand the mechanisms of drug release.

1. Mathematical models of drug
dissolution
Compiled by
Mr. Aher Sagar Atmaram
M. Pharm 1st Sem.
Department of pharmaceutics.
Guided by
Dr. A.R. Tekade
Head of the Department
Pharmaceutics and QAT.
1

2. Dissolution
• Dissolution is process in which a solid substance
solubilizes in a given solvent i.e. mass transfer from
the solid surface to the liquid phase.
• Importance of dissolution
 Dissolution test is used for evaluation of the drug
 Quantification of the amount and extent of drug
release from dosage form
2

3. Mathematical models used to determine
kinetics of drug release
i. Zero order model
ii. First order model
iii.Hixon- and Crowell model
iv.Higuchi model
v. Korsemeyer- peppas model
vi.Weibull model
vii.Baker-lonsdale model
viii.Gompertz model.
3

4. Zero order model
• The dissolution rate is independent on the concentration of the
drug undergoing reaction.
• Applicable to dosage forms that do not disaggregate and
releases drug slowly
W0 –Wt =Kt……..(1)
Where,
W0 =initial amount of drug dissolved
Wt= amount of the drug in the pharmaceutical
dosage form after time t.
Kt= is the proportionality constant.
4

5. • A graph is plotted between the time and the cumulative % of
drug release and it gives a straight line.
• It is applicable for systems such as several modified release
dosage forms like transdermal systems, matrix tablets with low
soluble drug, coated forms and osmotic systems.
5

6. First order model
• Proposed by –Gibaldi and Feldman (1967)
• First order – whose rate is directly depend on the concentration
of the drug administered.
• The release equation for first order is
Log Qt = Log Q0+ Kt /2.303
where
Q0 = initial amount of drug.
Qt = cumulative amount of drug release at time t.
K = first order release constant.
t = time in hours.
6

7. 7
• A graph is plotted between the time taken on x-axis and
the log cumulative percentage of drug remaining to be
released on y-axis and it gives a straight line.
• It is applicable for dosage forms containing water soluble
drugs in porous matrices.
7

8. Hixon and Crowell model
• Rate of dissolution depends on the surface of the solute, lesser
the surface area greater will be the dissolution
• Hixon and Crowell has derived a equation which expresses
dissolution rate based on the cube root of weight of particles
and radius of the particles is not assumed to be constant.
• Q0
1/3 - Qt
1/3 =kt
• Where
Q0 is the initial amount of drug in dosage form.
Qt is the remaining amount of drug in dosage form at time t.
k is the proportionality constant.
8

9. • A linear plot of the cube root of the initial concentration minus the
cube root of percent remaining versus time in hours for the
dissolution data in accordance with the Hixson-Crowell equation.
• It is applicable for erodible matrix formulation.
9

10. Higuchi model for drug release
• This is the first mathematical model which explains drug
release from matrix system.
• The Higuchi release equation is
Q=KH
where
Q = cumulative amount of drug release at time t.
KH = Higuchi dissolution constant.
t = time in hours.
• A graph is plotted between the square root of time( 𝒕)
taken on x-axis and the cumulative percentage of drug
release on y-axis and it gives a straight line
𝒕
10

11. • It is applicable for some transdermal systems and matrix
tablet with water soluble drugs
11

12. Korsemeyer Peppas model
• Korsmeyer derived a simple equation for drug release from a
controlled release polymeric system.
F= Km tn or F=Mt /M
• Where,
F is fraction of drug released at time t,
K is the release rate constant,
n is the release exponent,
Mt = Amount of drug released at time ‘t’
M = Total amount of drug in dosage form
12

13. • N value is used to characterize different
release for cylindrical shaped matrices,
Release exponent ( n ) Drug transport mechanism
n = 0.45 Fickian transport
0.45< n <0.89 Anomalous or non-fickian
transport
n = 0.89 Case-2 transport
n > 0.89 Super Case-2 transport.
Anomalous or non-fickian diffusion means rates of solvent
penetration and drug release in the same range.
Case 2 transport is when diffusion is rapid compared to
constant rate of solvent induced relaxation and swelling in the
polymer.
Case-2 relaxation or super case-2 transport refers to the
erosion of the polymeric chain.
13

14. • A graph between the log time on x-axis and the log cumulative
percentage of drug release on y-axis and it gives a straight line.
• It is applicable to linearization of release data from
microcapsules and microspheres 14

15. References
1. Ramteke KH, Dighe PA, Patil SV, mathematical models for
drug dissolution : A review, (SAJP), scholars academic and
scientific publishers, 2014 (3) 5, pg: 388-396.
2. Bramhankar DM, Jaiswal SB, Biopharmaceutics and
pharmacokinetics, Vallabh Prakashan, 2009,pg:431-433.
Thank you
15