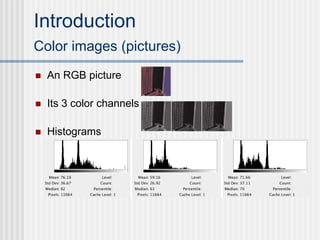
This document outlines the course "Digital Geometry and Image Processing" which focuses on geometric methods for analyzing digital images. The course is for graduate students in information engineering and will cover topics like metrics, adjacency graphs, topology, curves and surfaces in grids. It will use two primary textbooks and meet on Tuesdays and Thursdays. Selected additional topics will include moments, spatial relations, and properties of digital images.

1. Digital Geometry and Image Processing
Dietmar Saupe
Course Outline
SS 2006

2. Digital Geometry and Image
Processing (3V+2Ü)
 Geometric methods for digital picture analysis
 Scope: Graduate course
 Information Engineering master and PhD students
 Classes (Vorlesung), D. Saupe
 Tuesdays 8:15h-11h, Z714 (preliminary)
 Problem sessions (Übg.), V. Bondarenko
 Thursdays 14:00h-15:30h, Z714 (preliminary)

3. Primary course text book
 Reinhard Klette,
Azriel Rosenfeld
 Digital Geometry
 Morgan Kaufmann
(Elsevier) 2004
 UB will have copies

4. Secondary course text book
 R.C. Gonzales, R.E. Woods
 Digital Image Processing
 Prentice-Hall (2nd Ed.) 2002
 3rd edition
 UB has copies

5. Digital Geometry
Geometric methods for digital picture analysis
 Focus is on digital image or picture
analysis
 Core of the field
 Related mathematical fundamenals
 It is not
 yet another treatment of a very broad range
of problems, algorithms, heuristics, and
„useful“ technologies

6. Introduction
Color images (pictures)
 An RGB picture
 Its 3 color channels
 Histograms

7. Introduction
Early digital pictures
 A Greek pebble mosaic, detail from
“The Lion Hunt” in Pella,Macedonia,
circa 300 BC.
 Pattern woven by a Jacquard loom: a
black-and-white silk portrait of Jacquard
himself, woven under the control of a
“program” consisting of about 24,000
cards (one is shown on the left).
Early 19th century, before Babbage!

8. Introduction
Digital pictures in 2005
 Standard 16 Megapixel CCD cameras evolving
 Specialized cameras in photogrammetry of 100 Megapixels
 3D imaging modalities (CT, MRI, ...)
 3D-laser range scanners
 Leon Harmon of Bell Labs: picture of
Lincoln (252 pixels), “The Recognition
of Faces”, Scientific American, (Nov. 1973).
 A 380 degree panoramic picture of Auckland,
New Zealand, 2002,
500 Megapixels

9. Introduction
Grid of squares versus grid of points
 Two concepts for pixels (cells)
 Is the value a component of the pixel?
 A picture P is a mapping of a finite
rectangular grid region into the reals
 Generalization to 3D: voxel

10. Introduction
Adjacency
 Version 1
 Cell 1-adjacency and pixel 4-adjacency (left)
 Neighborhoods (right)
 Version 2
 Cell 0-adjacency and pixel 8-adjacency (left)
 Neighborhoods (right)
 In 3D:
 Cells? Voxels?

11. Introduction
Replace the X´s!
 Top:
 X-adjacent cells
 X-adjacent pixels
 Bottom:
 X-adjacent cells
 X-adjacent pixels

12. Introduction
Same in 3D!
 X-adjacent 3-cells :
 X= ? (left, middle, right)
 X-adjacent voxels :
 X= ? (left, right)

13. Introduction
Grid point connectivity
 Points are 4-connected? 8-connected?
 Background 4-connected? 8-connected?

14. Introduction
Equivalent classes
 Equivalence relation R on finite grid
 Reflexive, symmetric, transitive
 Yields equivalence classes
 For a picture P-equivalence:
 Pixels p,q: pRq iff P(p)=P(q)

15. Introduction
Component labelling
 Assume 4-adjacency of pixels
 Frequent task: label the 4-connected
components of the equivalence classes
 Some algorithms
 Fill algorithm:
 Rosenfeld-Pfaltz
labelling scheme

16. Introduction
Image scan sequences
 Examples:
 Space filling curves (Peano, Hilbert)

17. Topics (Chapters)
Metrics
 Basics: Norms, Minkowski metrics, integer valued
metrics, induced topology, Hausdorff metric
 Grid point metrics, paths, geodesics, intrinsic distances
 Metrics on pictures:
distance transforms
 medial axis

18. Topics (Chapters)
Adjacency graphs
 Graphs and connectedness, basic graph theory, Euler
characteristic and planarity
 Boundaries, cycles, frontiers in incidence pseudographs
 Inner (gray) pixel
border (black) pixel
co-border (gray) pixel

19. Topics (Chapters)
Topology
 Topological spaces, digital topologies
 Concepts homeomorphy, isotopy (top.
equivalence)
 Simplicial complexes, triangulations

20. Topics (Chapters)
Curves and surfaces: topology, geometry
 Jordan curves, curves in grids
 Surfaces and manifolds, ... in 3D grids
 Arc length, curvature, angles, areas
 Surfaces and solids
 Principal, gaussian, mean curvature
 Tracing surfaces

21. Topics (Chapters)
Curves and surfaces in grids
 Straightness, 2D and 3D
 Measuring arc length, curvature, corners
 Digital planes
 Measuring surface area, curvature

22. Selected Topics
 Moments and their estimation
 Other picture properties
 Spatial relations

23. Selected Topics (not covered)
 Hulls and diagrams (convexity, Voronoi)
 Transformations (t. groups, symmetries,
magnification, ...)
 Morphological operators (dilation, erosion,
simplification, segmentation, ...)
 Deformations (topological-preserving def.,
shrinking, thinning, ...)