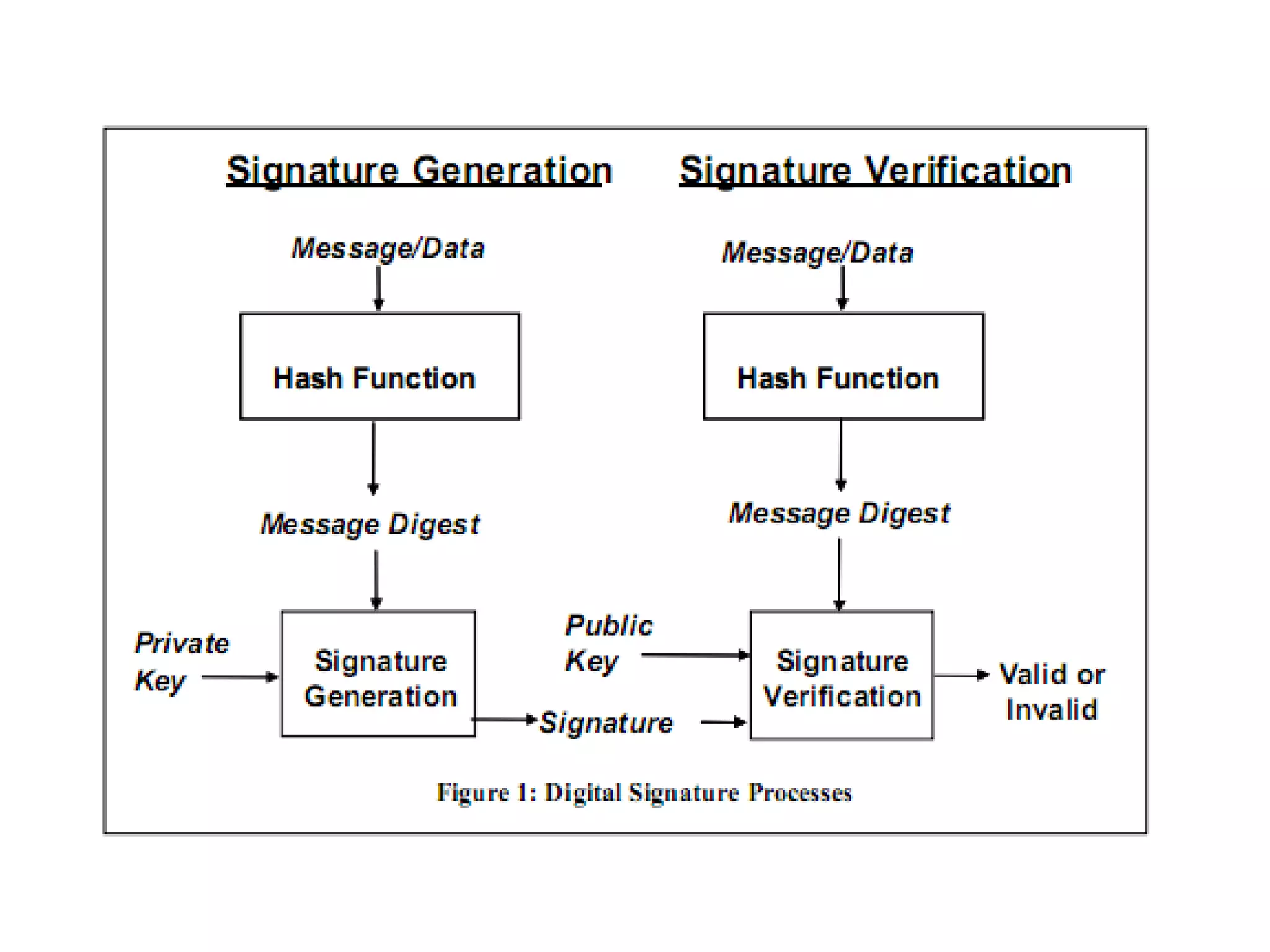
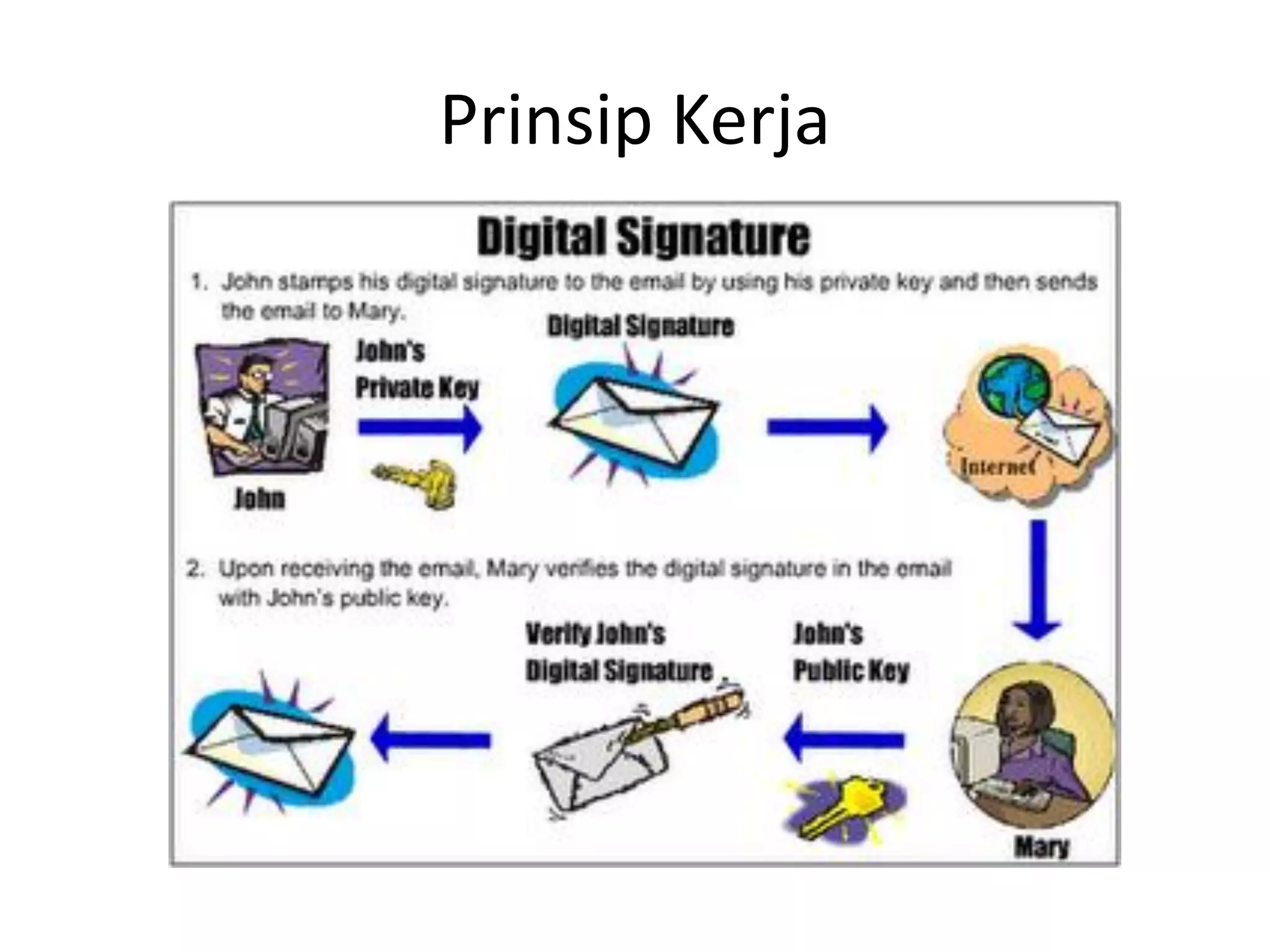
Dokumen ini menjelaskan prinsip kerja digital signature, termasuk metode RSA, ElGamal, Schnorr, dan standar digital signature. Setiap metode mencakup pembangkit kunci, algoritma tanda tangan, dan algoritma verifikasi, dengan penekanan pada keamanan dan struktur data. Contoh-contoh penerapan masing-masing algoritma disertakan untuk memperjelas cara kerja dan proses verifikasi.

1. Digital Signature

3. Prinsip Kerja

4. Layanan Keamanan
•Otentikasi Pesan : verify with true
•Keutuhan Data : dengan menambah fungsi hash.
•Non Repudation : tidak mungkin terjadi penolakan pesan yang telah ditandatangani

5. Algoritma Digital Signature RSA
a. Pembangkit Kunci : Menghasilkan kunci publik Kpublik = (e,n) dan Kunci Privat Kprivat = d.
b. Algoritma Sign : Menerima masukan sebuah pesan M, kunci privat dan kunci publik. Algoritma ini menggunakan eksponensial modular untuk mendapatkan signature ρ.
ρ= Mdmodn

6. Algoritma Digital Signature RSA
c. Algoritma verify : Bob mendapatkan ( m,ρ) dari alice, kemudian memverifikasi ( m,ρ) dengan menjalankan algoritma verify.
Input : ( m,ρ) , Kpublik = (e,n)
output : diterima
M’ = ρemod n
if M = M’ then
diterima = true
else
diterima = false
end if

7. Contoh
•Temukan signature pesan M = 32 dengan skema digital signature RSA, jika pada saat pembangkitan kunci alice mendapatkan Kpublik = (e,n) = (17,143) dan Kprivat = d = 113. Jelaskan juga bagaimana Bob melakukan verifikasi !!

8. Algoritma Digital signature ElGamal
a.Pembangkit Kunci : menetapkan kunci publik sebagai (α, β, p)dan kunci privat = d.
b.Algoritma sign : algoritma ini terlebih dulu memilih secara acak integer r yang nilai gcd(r,p) = 1, kemudian menghitung S1 dan S2.
Pilih r yang gcd (r , p-1)=1 dan 1 ≤ r ≤ (p-1)
S1 = αrmod p
S2 = ((M -d x S1) x r-1) mod (p-1) r-1: invers perkalian r pada Z*p-1.

9. c. Algoritma verify :
Input : (M, S1, S2), Kpublik = (α, β, p)
output : diterima
V1= αMmod p
V2= βS1x S1S2mod p
if V1= V2mod p then
diterima = true
else
diterima = false
end if

10. Contoh
•Apa signature yang dikembalikan algoritma sign skema digital signature ElGamal bila kunci privat adalah d = 2, kunci publik adalah (α= 7, β= 18, p = 31) dan dokumen M = 100? Tunjukkan juga jalannya algoritma verify setelah mendapatkan pesan dan signature.

11. Digital Signature Schnorr
•Merupakan skema digital signature ElGamal dengan ukuran signature yang lebih kecil dan keamanan yang lebih baik. Skema ini menggunakan fungsi hash untuk mengakses ukuran pesan dan juga mendapatkan tingkat keamanan yang lebih baik.

12. Algoritma digital signature Schnorr
a.Pembangkit kunci :
pilih bilangan prima p { 512 < |p| ≤ 1024}
pilih bil prima q yg membagi habis (p-1) ((p-1)=0 mod q)
Pilih akar primitif b pada GF(p).
α= b(p-1)/q
pilih d
β= αd
Kpublik = (α, β, p, q), Kprivat = d

13. b. Algoritma Sign Schnorr :
Input : M, Kprivat = d, Kpublik = (α, β, p, q).
Output : S1, S2 {signature}.
Pilih r {1 ≤ r ≤ q}
S1= h (M|αrmod p)
S2= (r + d x S1) mod q

14. c. Algoritma verify Schnorr :
input: (M, S1, S2), Kpublik = (α, β, p, q).
Output : diterima
V = h(M|αS1β-S2mod p)
if V = S1 mod q then
diterima = true
else
diterima = false
end if

15. Contoh
1. Dengan menggunakan kunci publik (α= 16 , β= 2, p = 31, q = 5). Dan kunci privat d = 4. Lakukan algoritma sign dan verify untuk dokumen M = 20 dengan skema digital signature Schnorr?

16. Digital Signature Standard
a.Algoritma pembangkit kunci sama dengan Schnorr, hanya saja ukuran bilangan prima p merupakan kelipatan 64. algoritma ini menggembalikan Kpublik = (α, β, p, q), dan Kprivat = d.
b.Algoritma Sign.
Pilih r {1 ≤ r ≤ q}
S1 = (αrmod p) mod q.
S2 = (h(M) + dS1) r-1mod q.

17. c. Algoritma verify :
Input : (M, S1, S2), Kpublik = (α, β, p, q).
Output : diterima
V = (αh(M)S2-1βS1S2-1mod p) mod q)
if V = S1 mod q then
diterima = true
else
diterima = false
end if

18. Contoh
1. Misalnya pembangkit kunci skema digital signature DSS memberikan pasangan kunci, yaitu kunci publik = (α= 77, β= 1350, p = 3527, q = 43). Dan kunci privat d = 50. Jika terdapat pesan M dan nilai h(M) = 100, apa nilai signature dan tunjukkan jalannya algoritma verify?