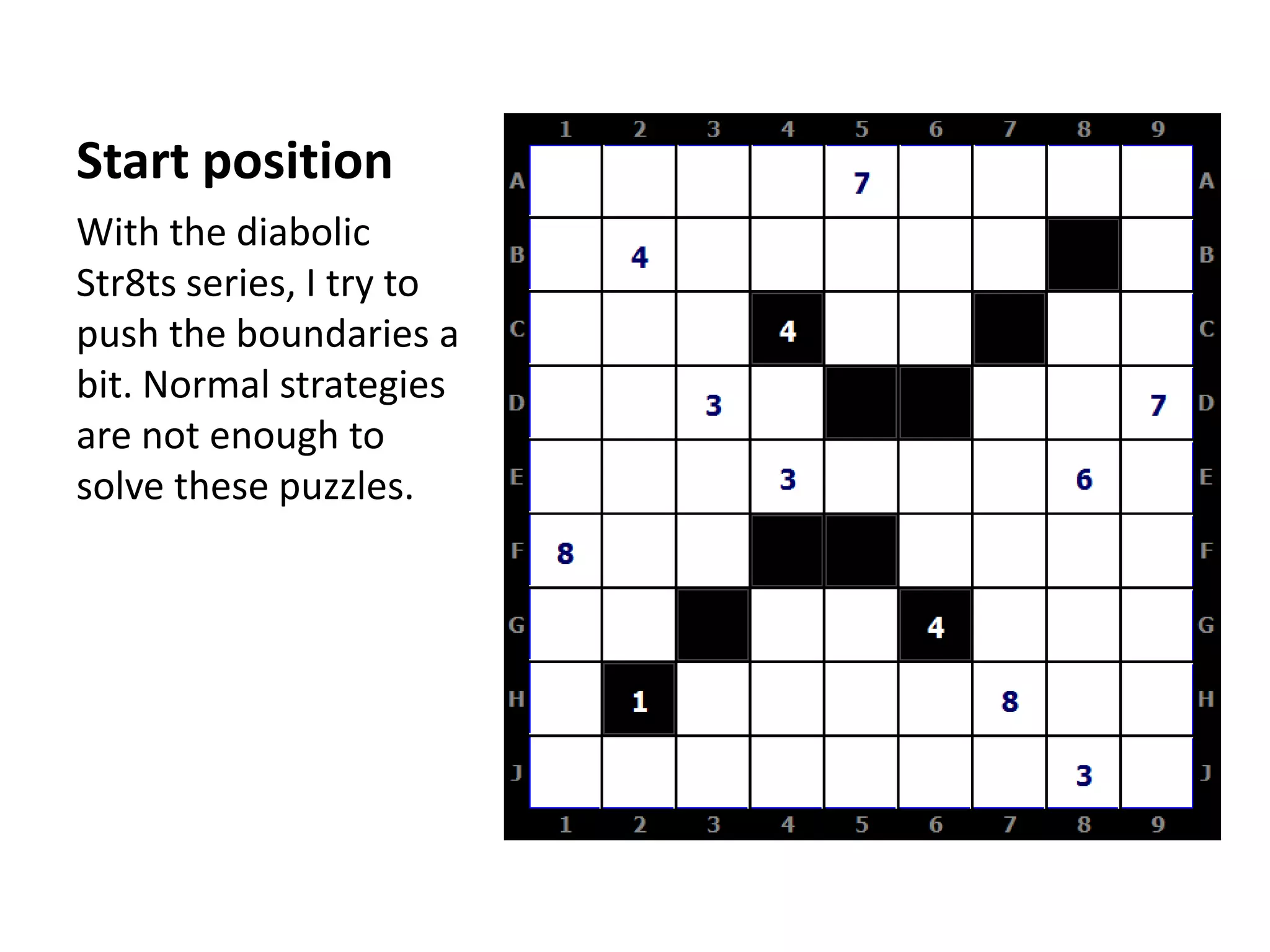
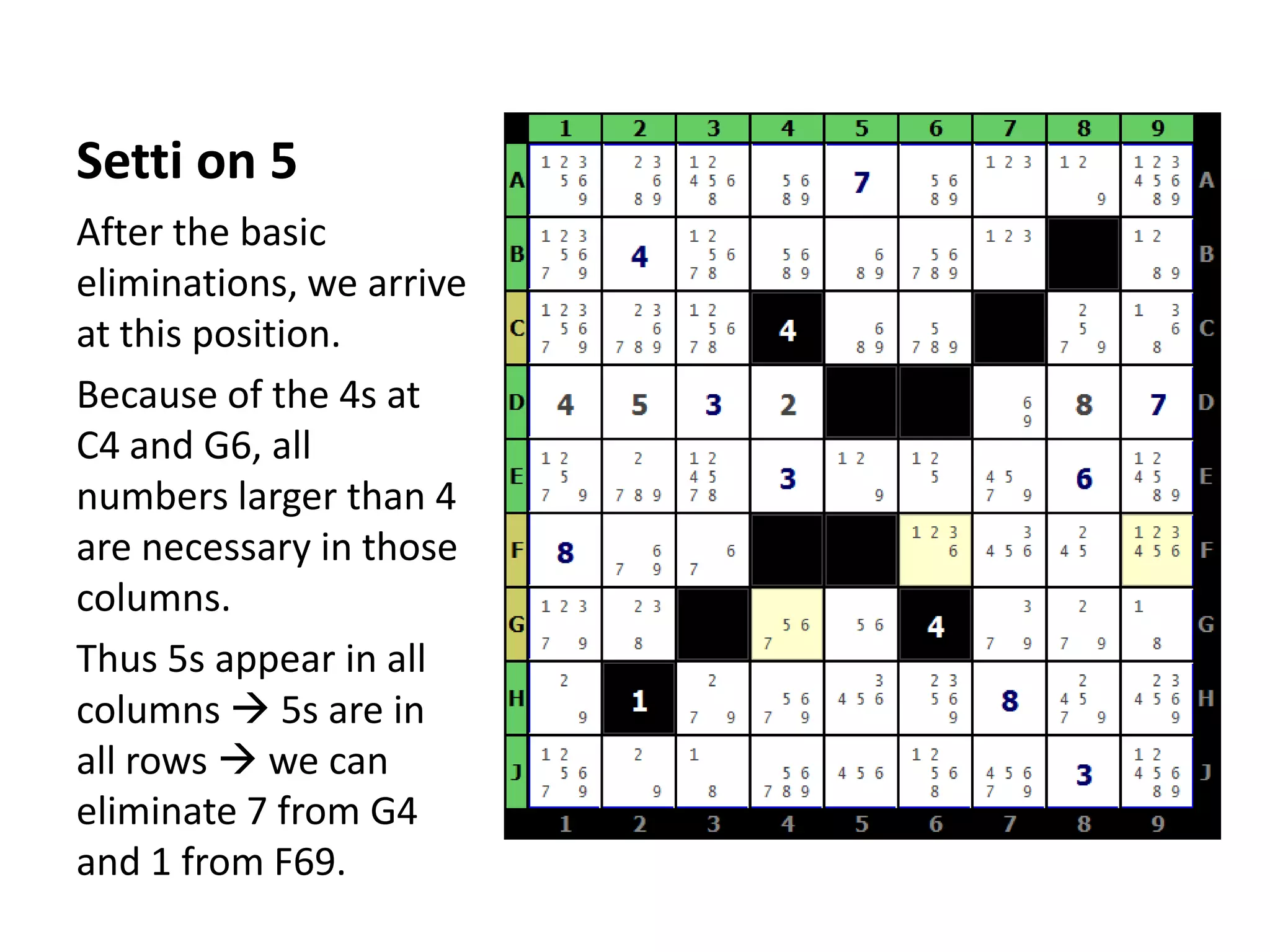
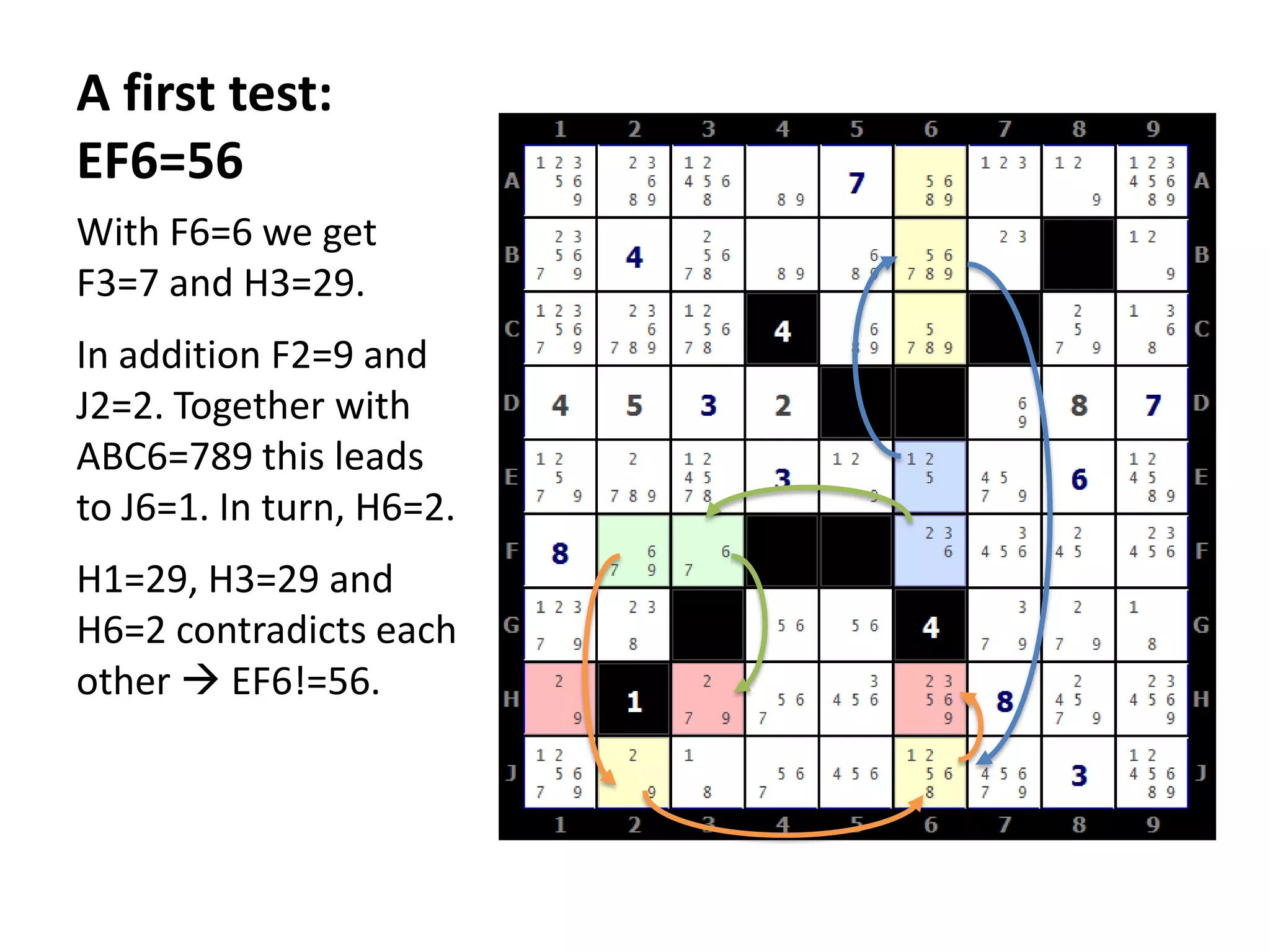
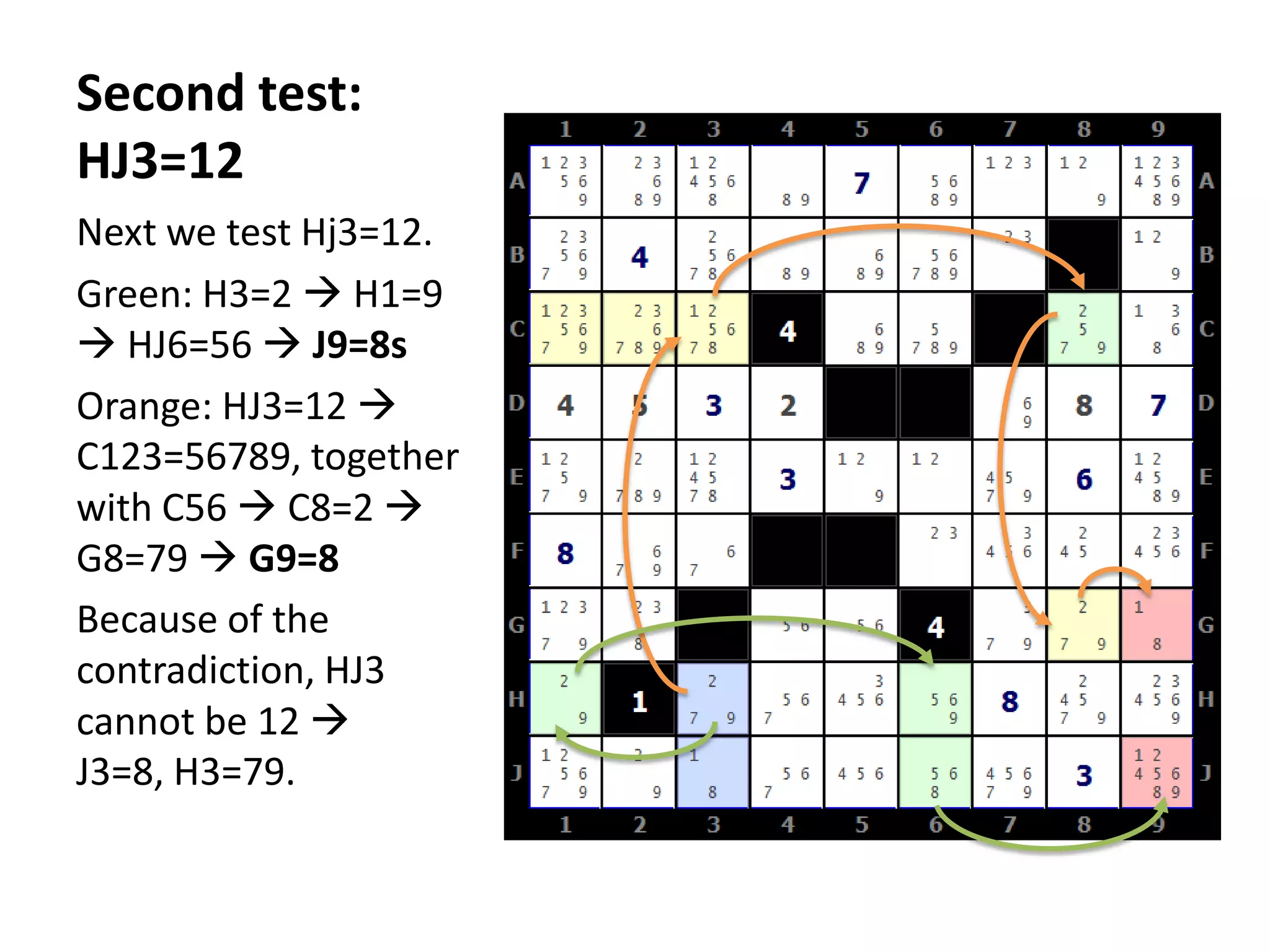
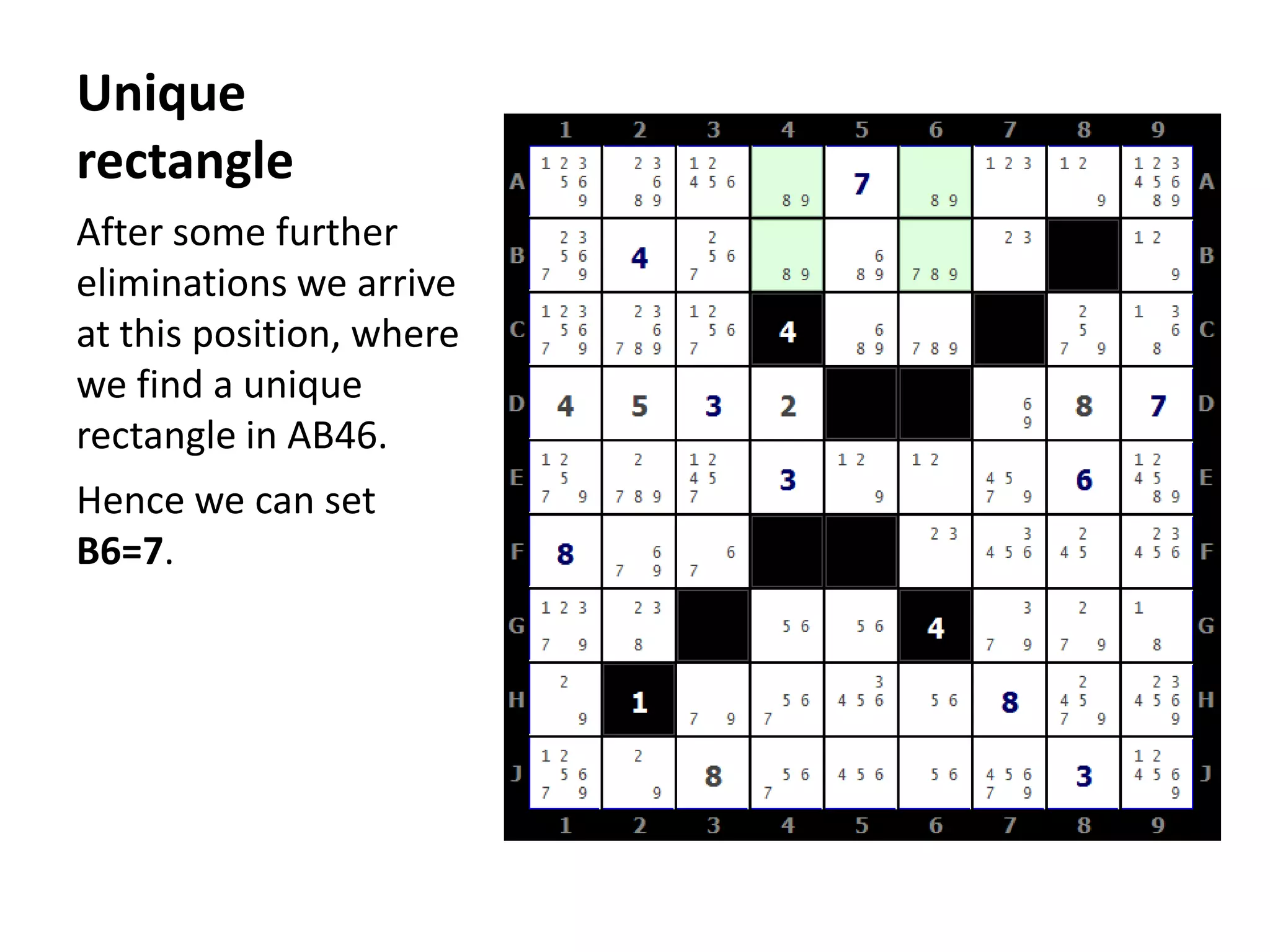
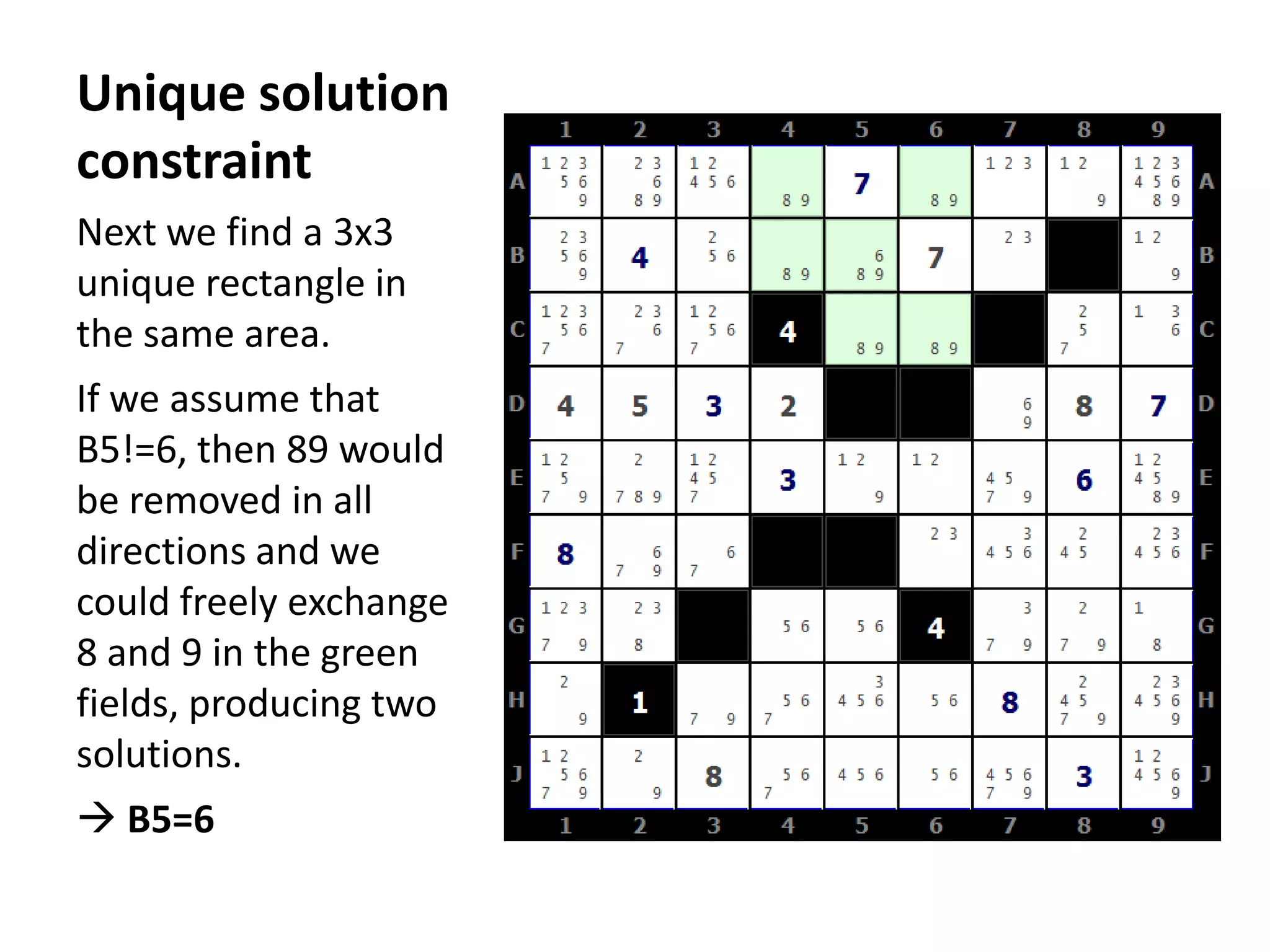
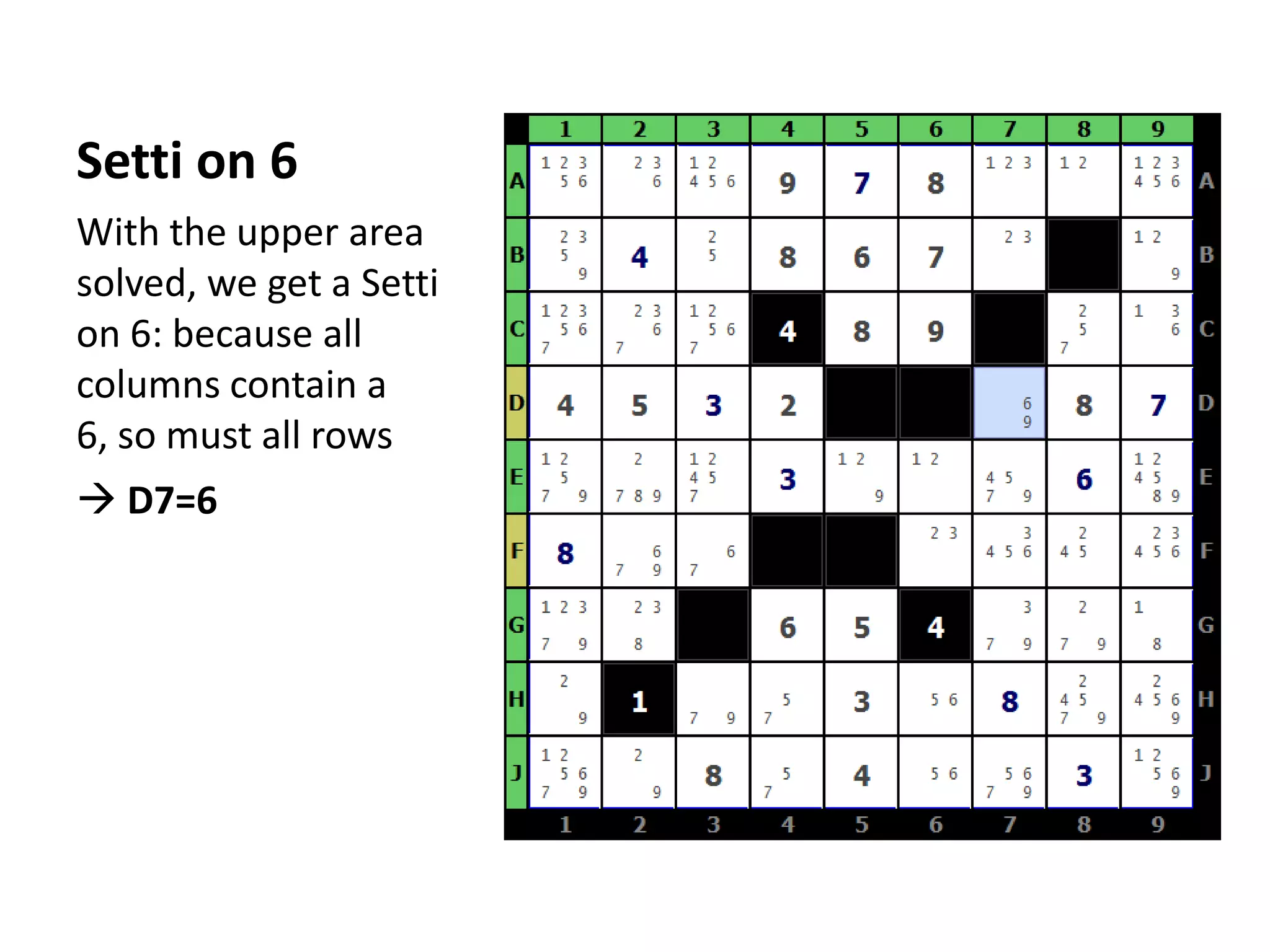
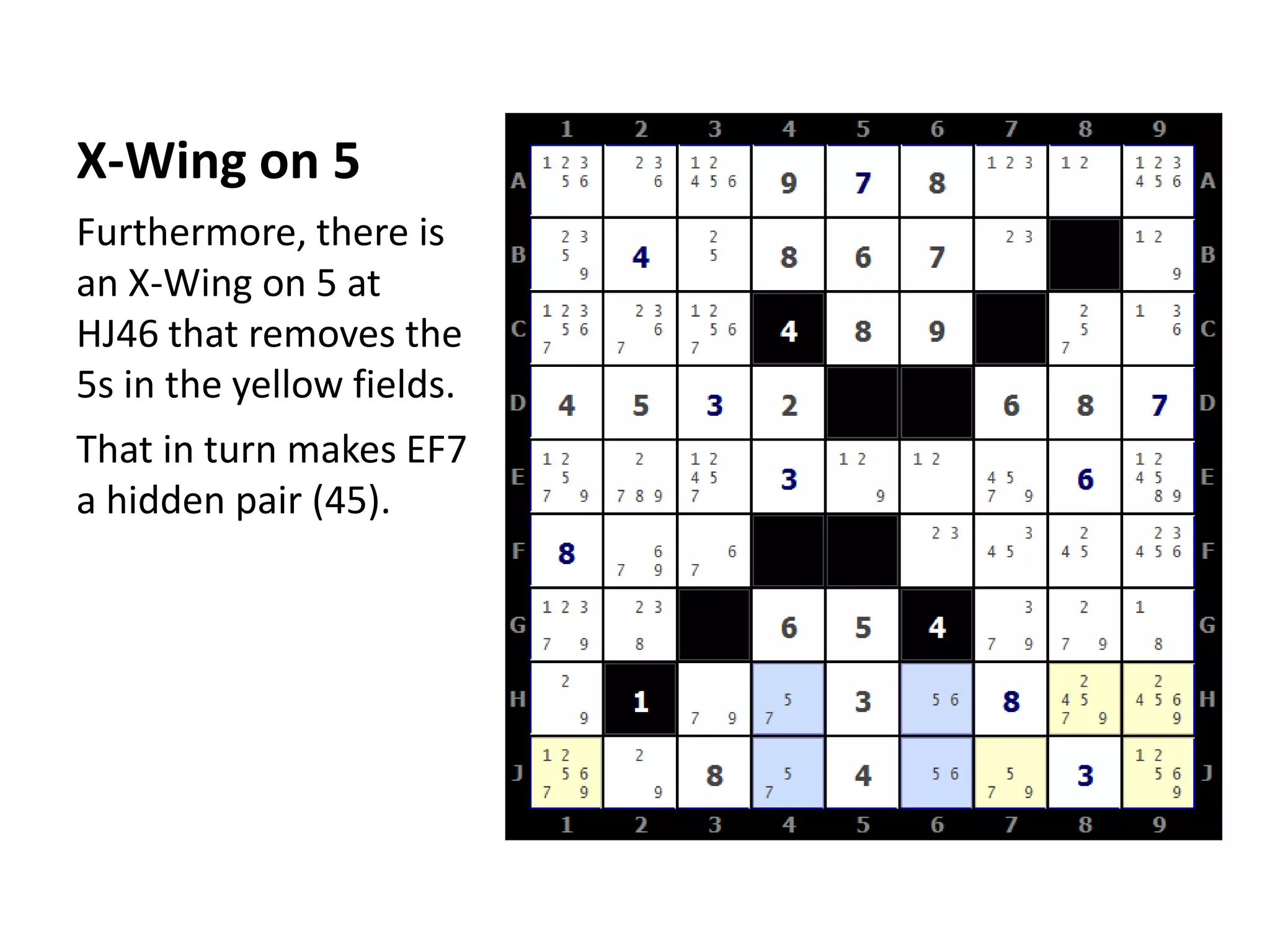
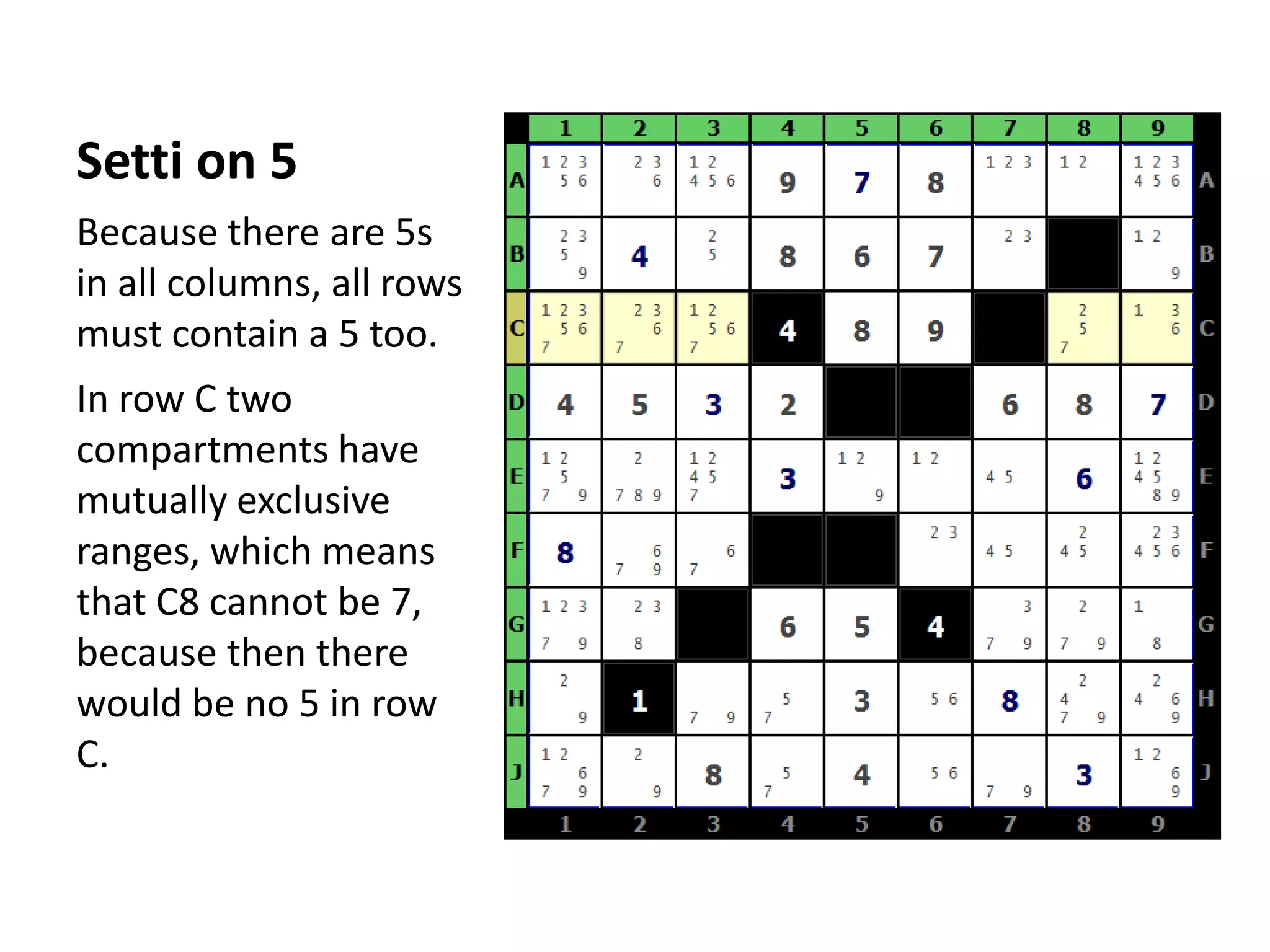
This document summarizes the steps to solve a difficult Str8ts puzzle called Diabolic Str8ts Puzzle #5. It begins with the starting position and notes that normal strategies are not enough. Through a series of logical deductions using strategies like unique rectangles, X-Wings, jellyfish, and Setti's rule, it arrives at the unique solution. Advanced strategies had to be used due to the boundaries being pushed in this diabolical puzzle.

1. Diabolic Str8ts Puzzle #5Puzzle & solutionbySlowThinker

2. Start positionWith the diabolic Str8ts series, I try to push the boundaries a bit. Normal strategies are not enough to solve these puzzles.

3. Setti on 5After the basic eliminations, we arrive at this position.Because of the 4s at C4 and G6, all numbers larger than 4 are necessary in those columns.Thus 5s appear in all columns  5s are in all rows  we can eliminate 7 from G4 and 1 from F69.

4. A first test: EF6=56With F6=6 we get F3=7 and H3=29.In addition F2=9 and J2=2. Together with ABC6=789 this leads to J6=1. In turn, H6=2.H1=29, H3=29 and H6=2 contradicts each other  EF6!=56.

5. Second test: HJ3=12Next we test Hj3=12.Green: H3=2  H1=9  HJ6=56  J9=8sOrange: HJ3=12  C123=56789, together with C56  C8=2  G8=79  G9=8Because of the contradiction, HJ3 cannot be 12  J3=8, H3=79.

6. Unique rectangleAfter some further eliminations we arrive at this position, where we find a unique rectangle in AB46.Hence we can set B6=7.

7. Unique solution constraintNext we find a 3x3 unique rectangle in the same area.If we assume that B5!=6, then 89 would be removed in all directions and we could freely exchange 8 and 9 in the green fields, producing two solutions. B5=6

8. Setti on 6With the upper area solved, we get a Setti on 6: because all columns contain a 6, so must all rows D7=6

9. X-Wing on 5Furthermore, there is an X-Wing on 5 at HJ46 that removes the 5s in the yellow fields.That in turn makes EF7 a hidden pair (45).

10. Settion 5Because there are 5s in all columns, all rows must contain a 5 too.In row C two compartments have mutually exclusive ranges, which means that C8 cannot be 7, because then there would be no 5 in row C.

11. Jellyfish on 7With the 7 removed from C8 we get a jellyfish on 7 at GHJ478 that removes the 7s from the yellow fields.

12. Jellyfish on 7 continuedFurthermore, because of the jellyfish, 7 is not only a sure candidate in the columns of the jellyfish, but also in its rows. (As there is simply no way to place three 7s in the yellow fields without placing one 7 in row G). G789 must be 789 and G12=123

13. SolutionAfter this the puzzle can be solved using basic strategies.

14. GlossaryLetters appended to steps indicate the last strategy used, just before filling in a field:No letter … number was last candidate in fields … single (last) candidate for that number in compartmentc … compartment range checkd … stranded (unreachable/impossible) digits removedh … high/low range check across compartmentsp/t/q … naked pair / naked triple / naked quadrupleph/th/qh … hidden pair / hidden triple / hidden quadruplex … X-wing (2 rows / 2 columns)w … Swordfish (3 rows / 3 columns)j … Jellyfish (4 rows / 4 columns)L … large gap fieldSx … Setti’s rule (count the numbers rule) – ‘x’ is the analysed numberu … unique rectangley … Y-Wing or XY-chains

15. Diabolic Str8ts Puzzle #5Solution by SlowThinkerNote: there are other (maybe easier) ways to solve this puzzle.View & download my strategy slides from:http://slideshare.net/SlowThinker/str8ts-basic-and-advanced-strategiesor from Google Docs:http://is.gd/slowthinker_str8ts_strategy