Download to read offline
Uploaded byArtem Shoobovych
Detekcja kolizji
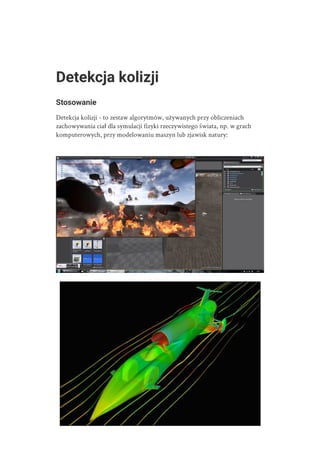
Detekcja kolizji w 2D grafice. Wprowadzenie do algorytmów detekcji kolizji na płaszczyźnie. Podstawowe formy opisujące obiekty. Uproszczenie formy obiektu w celu optymalizacji algorytmów wykrycia kolizji. Obejmuje takie tematy jak: 2D rigid body collision detection, raycasting, continuous collision detection, soft bodies.
Detekcja kolizji
- 1. Detekcja kolizji Stosowanie Detekcja kolizji- to zestaw algorytmów, używanych przy obliczeniach zachowywania ciał dla symulacji fizyki rzeczywistego świata, np. w grach komputerowych, przy modelowaniu maszyn lub zjawisk natury:
- 2. Algorytmy Żeby sprawdzić czydwa ciała się dotykają, należy najpierw stworzyć model tych ciał, czyli opisać ich formę. Formę obiektu można opisać w zależności od tego, jaki cel chcemy osiągnąć: jeśli nam nie bardzo zależy na tym, żeby obiekt dokładnie reagował na kolizję, możemy bardzo uprościć jego formę, wynikiem czego nadal będzie jakaś reakcja na kolizję, ale ona nie będzie miała pełnej fizycznej dokładności. Natomiast będzie łatwo obliczyć zachowanie takiego obiektu. Tak to jest zrobione między innym w grach - im słabsze urządzenie, na którym działa program - tym mniej obliczeń można robić, żeby, na przykład, zachować baterię. Przykład: w grach komputerowych często stosują technologię Character Controller. To jest uproszczenie formy bohatera gry do kapsuły:
- 3. Przy takim uproszczeniudość łatwo można wykryć, czy bohater uderzył o schody, czy o ścianę. Tej formy stosują do wykrycia przesuwań bohatera. Na obrazku można zobaczyć wiele innych form (kubów), które również opisują bohatera - ale oni są używani do wykrycia innej części kolizji - na przykład w strzelance dla wykrycia urażeń. Ale te kuby również nie opisują model bohatera dokładnie - natomiast są dużym uproszczeniem jego formy. W takim układzie, model bohatera nie odpowiada swojej modeli fizycznej na 100%, ale tego wystarcza, żeby bohater reagował na kolizję ze ścianą czy ziemią, na przykład:
- 4. Dla większego efektu(w filmach, bajkach, najnowszych grach) oprócz modeli kapsuły, osobne części modeli bohatera są opisane przy pomocy swoich niezależnych fizycznych modeli, żeby na przykład ustalić nogę bohatera w potrzebnym miejscu przy chodzeniu po skosach:
- 5. Sprawdzenie przecinania obiektów Ogólniemówiąc, żeby sprawdzić zestaw obiektów na przedmiot kolizji / przecięcia / dotkania, należy dla każdej pary obiektów sprawdzić czy przecinają / dotykają się ich formy (collision shape). Ten algorytm jest o złożoności O(n^2) bo dla każdego z Nobiektów będzie odpalono N - 1testów kolizji. Można przyspieszyć ten algorytm, rozpraszając go - w przypadku wyłącznie detekcji kolizji to nie stanowi problemu. Ale w rzeczywistości często należy w jakiś sposób zreagować na kolizję - zmienić pozycję obiektu lub wyświetlić jakiś efekt.
- 6. Więc, im prostsząformę ma obiekt, tym szybszy będzie ten proces. Odpowiednio, im mniej obiektów należy sprawdzić - tym szybszy będzie ten proces. Forma obiektu Dla detekcji kolizji należy wiedzieć, gdzie się znajduje obiekt (pozycja) i jaką ma formę. Obiekt jest opisany przy pomocy tych dwóch parametrów. Często obiekt nie zmienia swojej formy w trakcie działania programu, ale może się obracać. Ogólnie, obrócony obiekt ma inną formę z matematycznego punktu widzenia - obrócony, powiedzmy, prostokąt, opisuje się innym zestawem formuł. W rzeczywistości ten sam obiekt może natomiast mieć trzy parametry - pozycję, kąt obrócenia i formę. 2D Let's talk about 2D. W dwu-wymiarowej grafice obiekty są płaskie. Dlatego opisanie ich formy nie stanowi dużego problemu. Natomiast, żeby sprawdzić czy dwie różne formy się przecinają, należy opisać algorytmy dla sprawdzania czy dowolny punkt obiektu A dotyka się czy przecina się z dowolnym punktem obiektu B. W praktyce rzadko stosują takich dokładnych sprawdzań. Natomiast stosują algorytmy wzajemnego sprawdzania przecięcia podstawowych jednostek form, np. koło-koło, koło-trójkąt, trójkąt-trójkąt. Tych dwóch form i trzech testów wystarczy, żeby wykryć kolizje pomiędzy większością obiektów w 2D, ponieważ inne formy są kombinacjami z kół czy trójkątów:
- 7. KOŁO Koło jest najprostsząformą dla detekcji kolizji. Tą formę możemy opisać używając jednego parametru: promieniu. I jak byśmy nie skręciliśmy koło - ono ma tą samą formę. Sprawdzenie czy dwa koła się przecinają jest dość łatwe - wystarczy rozwiązać takie równanie:
- 8. W przypadku ztrójkątem to nie jest taki banał: Jak widać na zdjęciu - jest dość sporo możliwych pozycji trójkąta odnośnie koła, więc sprawdzenie nie będzie takie łatwe. Jest kilka możliwości implementacji takiego testu. Można, na przykład, znaleść wszystkie (trzy) długości wektorów normalnych od centru koła do każdej ze stron trójkąta i sprawdzić czy długość tego wektoru mniejsza lub równa promieniu koła i czy trafia koniec tego wektoru do odpowiedniej strony trójkątu:
- 9. Na obrazku wyżejna zielono pokazany promień koła, na niebiesko - samo koło, na czerwono - wektory normalne do każdej ze stron trójkąta. Jak widać, każdy z wektorów jest krótszy od promienia koła, ale tylko jeden z nich trafia na stronę trójkąta. Więc można stwierdzić, że obiekty przecinają się: Dla czego jest warunek trafienia do strony trójkąta: Tu widać, że jeden z wektorów normalnych jest krótszy od promienia koła, ale nie trafia na stronę trójkąta, do której on jest perpendykularny. Więc nie można stwierdzić, że trójkąt przecina się z tym kołem. Ale ten algorytm ma podstawową wadę: nie da się wykryć przy jego pomocy takiej sytuacji:
- 10. Każdy z wektorówjest dłuższy od promienia koła, ale wciąż koło jest wewnątrz trójkąta. Żeby usunąć tą wadę, można dodać takie sprawdzenie: czy suma powierzchni trójkątów od wierzchołków zewnętrznego trójkąta do centru koła rowna się powierzchni całego zewnętrznego trójkąta: Trójkąt Wyżej już było opisano jak wykryć kolizję między trójkątem a kołem. W przypadku dwóch trójkątów można stosować algorytmu sumy powierzchni, jak to było opisano dla koła. Tylko że tym razem trzeba będzie sprawdzić to dla każdego wierzchołka trójkąta:
- 11. Jedną z ciekawszychsytuacji będzie taka, gdy trójkąty się tylko dotykają: W takim razie należało by sprawdzić, czy chociażbym jedna ze stron trójkąta nie zawiera (części) dowolnej strony innego trójkąta. Złożone formy Pozostałe formy obiektów można przedstawić jako kombinację z trójkątów i/lub kół i stosować odpowiednich algorytmów do każdego elementu całości. Na przykład, prostokąt. Prostokątowa forma obiektu, czyli box shape, może być przedstawiona albo jako zestaw z dwóch trójkątów, albo jako prostokąt.
- 12. Tylko że wykrycieprzecinania prostokąta i innych form będzie bardziej skomplikowane. Albo kapsuła - to jest kombinacja z dwóch trójkątów i dwóch kół: Convex & Concave Istnieje dwa rodzaje form obiektów - wypukłe i wklęsłe. W przypadku wypukłych obiektów, wykrycie kolizji można przyspieszyć, na przykład, sprawdzając, czy przecinają się granicy obiektów. Albo sprawdzać czy dwa obiekty się przecinają, biorąc pod uwagę w jakiej płaszczyźnie leży obiekt odnośnie stron innego obiektu:
- 13. Jeśli obiekt HIJKLMleżyw innej płaszczyźnie, niż obiekt ABCDEFG- obi się nie przecinają. Wyliczenie w jakiej płaszczyźnie znajduje się obiekt zrobione poprzez wyznaczenie płaszczyzn, zdefiniowanych każdej ze stron obiektu. Dość ważną formą jest także triangle mesh. To jest taka forma obiektu, która się składa z wielu trójkątów i jest wklęsłą. Dlatego ta forma jest najtrudniejsza do analizy na przedmiot wykrycia kolizji. W praktyce takich form stosują tak rzadko, jak możliwe ponieważ choć dają one najbardziej dokładny efekt, ale są trudne obliczeniowo. Dlatego takie formy stosują do plansz: Raycasting Czasem trzeba nie sprawdzić, czy dwa obiekty się przecinają lub dotykają się,
- 14. Czasem trzeba niesprawdzić, czy dwa obiekty się przecinają lub dotykają się, ale czy oni zetkną się w przyszłości. Lub, ewentualnie, sprawdzić odległość pomiędzy dwoma obiektami. To zadanie rozwiązuje algorytm raycastingu. To jest wykrycie, czy promień, puszczony z punktu A przekroczy się z dowolnym innym obiektem i, jeśli przekroci się, to w jakim punkcie. Przy pomocy raycastingu jest możliwe także wyliczenie najkrótszej odległości między obiektami w pewnym kierunku: Dla każdego obiektu będzie sprawdzono, czy promień przekrocił formę tego obiektu. Znalezenie punktów przekrocenia promienia może być implementowane przy użyciu wektorów. Niech mamy formę koła, opisaną promieniem roraz centrem ci promień, puszczony z punktu ow kierunku l. Wtedy możemy opisać punkt x, który leży na kole i w którym przecina się koło i promień: W tym układzie mamy dwie nieznane zmienne: xoraz d. Jeśli przyrównamy oba równania i rozwiążemy ostateczne, zobaczymy: W przypadku trójkąta, dowolny punkt wewnątrz trójkąta, zdefiniowanego
- 15. W przypadku trójkąta,dowolny punkt wewnątrz trójkąta, zdefiniowanego wierzchołkami p1, p2i p3można przedstawić parametrycznie: Dla promienia o długości d, puszczonego z punktu ow kierunku l, mamy trzy nieznane zmienne: u, voraz d. Istnieje dość szybki algorytm wykrycia istnienia punktu x dla tego przypadku, algorytm Mollera-Trumborea. Ciągłe wykrycie kolizji Wyżej wymienione algorytmy są stosowane do ciągłej detekcji kolizji. W rzeczywistości uaktualnienie stanu obiektów jest robione dyskretnie, to znaczy że każdy obiekt uaktualnia swoją pozycję, powiedzmy, co Nsekund. Ale w świecie rzeczywistym tak się nie dzieje - obiektu ruszają się ciągle. I w przypadku, gdy obiekt rusza się bardzo szybko, przy następnym uaktualnieniu stanu obiektu na komputerze on pojawi się w co innej pozycji niż oczekiwane: Ale w świecie rzeczywistym to bym wyglądało tak:
- 16. Dlatego stosują raycastingu- przy poruszaniu obiektu o dużej prętkości najpierw jest puszczany promień przed tym obiektem i jest sprawdzane, czy należy ten obiekt zatrzymać wcześniej, czy nie. Miękkie ciała Czasem jest potrzeba zasymulować miękkie ciało - oponę koła czy piłkę. To są ciała, które zmieniają swoją formę kolizji: Jak można się domyślić, nie jest to łatwe zadanie, więc w celu optymizacji często stosują technik, które tworzą wrażenie, że ciało jest miękkie, ale nie zmieniają rzeczywistej formy obiektu. To jest zrobione przy pomocy stawów (joints) albo sprężyn, które łączą składowe formy obiektu, formując bardzo podobną formę. Dokładniej to można zobaczyć na tym obrazku:
- 17. Tu widać, żei zając i kola są złożone z dużej ilości trójkątów. Każdy z tych trójkątów jest połączony z innymi przy pomocy niewidocznych sprężyn. W momencie, gdy koło uderza się o schody, trójkąty się zbliżają pod wpływem sprężyny i użytkownikowi się wydaje, że koło zmieniło swoją formę.