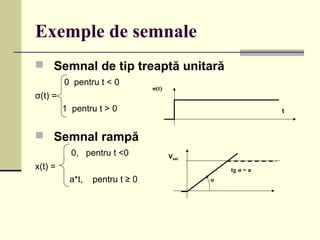
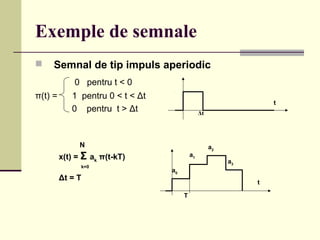
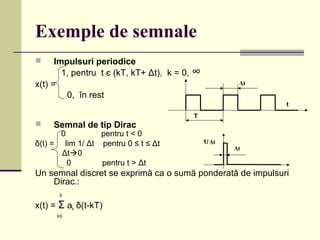
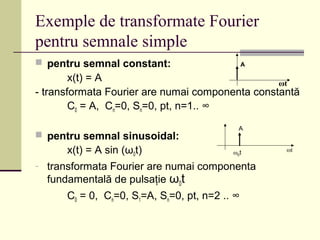
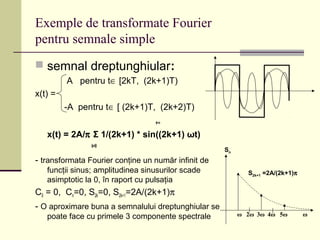
Cursul 9 de informatică industrială abordează procesarea semnalelor, inclusiv extragerea și transformarea componentelor semnalelor, clasificarea lor în funcție de predictibilitate, continuitate și amplitudine. Se discută despre analiza și sinteza semnalelor, sisteme liniare și neliniare, precum și despre transformatele Fourier pentru semnale periodice și aperiodice. De asemenea, sunt prezentate proprietățile transformatei Fourier și aplicabilitățile sale în evaluarea efectului sistemelor liniare asupra semnalelor complexe.

1. Informatica industriala
Cursul 9 Prelucrarea digitala a semnalelor

2. Procesarea semnalelor
 Obiective:
 extragerea din semnal a unor componente considerate relevante
pentru problema studiată (ex.: filtrare),
 transformarea semnalului pe baza unei anumite reguli
(amplificare/atenuare, întârziere, etc.).
 Domenii:
 Analiza semnalelor - domeniul care se ocupă de descompunerea
semnalelor complexe în semnale elementare
 Un semnal complex se descrie ca o suma (ponderata) de semnale
simple; (ponderea=amplitudinea semnalului simplu)
 Sinteza semnalelor - generarea unor semnale complexe, cu
anumite proprietăţi date, care se obţin prin combinarea unor
semnale elementare.
 Ex: modulatoare, multiplexare, generatoare de semnal, etc.

3. Semnale
 Def.: semnal - o mărime fizică purtătoare a unei informaţii
 Clasificare:
 Din punct de vedere al predictibilităţii, semnalele pot fi:
 deterministe, dacă evoluţia lor este previzibilă şi se pot descrie
prin funcţii de timp (ex.: x(t) = A sin(ωt+φ))
 aleatoare, dacă au o evoluţie imprevizibilă sau mult prea
complexă pentru a putea fi exprimată printr-o expresie
matematică (ex.: zgomot)
 Din punct de vedere al evoluţiei în timp semnalele pot fi:
 continue, dacă sunt descrise prin funcţii continue de timp
 discrete, dacă au valori definite doar la anumite momente de
timp
 Din punct de vedere al amplitudinii semnalele pot fi :
 continue, dacă domeniul de variaţie al amplitudinii este un
interval continuu
 cuantizate, dacă amplitudinea poate lua un număr finit de
valori

4. Semnale
 Semnale analogice - semnalele continue în timp şi ca domeniu de
valori
 Se studiaza in teoria clasica a semnalelor (integrale/derivate
continue, transformata Fourier, Laplace, etc.)
 Semnale digitale – semnale discrete din punct de vedere al evoluţiei în
timp şi cuantizate ca domeniu de valori sunt denumite
 Se studiaza prin teoria semnalelor digitale sau discrete (sume
integrale, transformata in Z, etc.)
t
t
t
t
x(t)
x(t)
x(nT)
x(nT)
Continuu Discret
Continuu
Cuantizat
timp
amplitudine

5. Sisteme liniare
 Sisteme descrise prin ecuatii integro-diferentiale liniare
 Sisteme la care este valabil principiul suprapunerii efectelor:
 Efectul unui semnal complex asupra unui sistem este egal cu suma
efectelor produse de semnalele simple ce compun semnalul
complex
 Efectul produs de un sistem liniar asupra unui semnal complex de
intrare este egal cu suma efectelor produse asupra componentelor
semnalului
 Sisteme reale:
 Neliniare in ansamblu
 Linearizabile pe portiuni
 Cauze de neliniaritate:
 Efect de saturatie (la valori prea mari)
 Legea de variatie a sistemului este neliniara prin natura
fenomenelor incorporate
 Transformari de stare (ex: fierbere, rupere, etc.)

6. Exemple de semnale
(in domeniul continuu)
 Semnal sinusoidal
x(t) = A sin(ωt+φ) = A sin (2πf*t + φ) = A sin (2π/T * t + φ)
unde: A – amplitudinea semnalului
ω – pulsaţia
φ – faza iniţială a semnalului
f – frecvenţa semnalului
T – perioada
t – timpul
φ
A
x(t)
t

7. Exemple de semnale
 Semnal de tip treaptă unitară
0 pentru t < 0
σ(t) =
1 pentru t > 0
 Semnal rampă
0, pentru t <0
x(t) =
a*t, pentru t ≥ 0
σ(t)
t
Vsat
tg α = a
α

8. Exemple de semnale
 Semnal de tip impuls aperiodic
0 pentru t < 0
π(t) = 1 pentru 0 < t < Δt
0 pentru t > Δt
t
Δt
a0
a1
a2
a3
T
t
N
x(t) = Σ ak
π(t-kT)
k=0
Δt = T

9. Exemple de semnale
 Impulsuri periodice
1, pentru t є (kT, kT+ Δt), k = 0, ∞
x(t) =
0, în rest
 Semnal de tip Dirac
0 pentru t < 0
δ(t) = lim 1/ Δt pentru 0 ≤ t ≤ Δt
Δt0
0 pentru t > Δt
Un semnal discret se exprimă ca o sumă ponderată de impulsuri
Dirac.:
N
x(t) = Σ ak δ(t-kT)
k=0
T
t
Δt
Δt
1/ Δt

10. Semnale in domeniul discret
 Semnal discretizat in timp: secventa de valori ale semnalului la
momente kT (T- perioada de esantionare a semnalului)
 Exemple:
a. Semnal sinusoidal discret
x(kT) = A sin(ω*kT+φ)
b. Semnal treaptă unitară în domeniul discret
0, pentru k < 0
σ(kT) =
1, pentru k ≥ 0
c. Impuls Dirac discret
1, pentru k = 0
δ(kT) =
0, pentru k ≠ 0

11. Analiza semnalelor
 Aproximarea semnalelor
 Un anumit semnal x(t) se poate descompune într-un
număr finit sau infinit de funcţii elementare
N
x(t) = Σ an
* fn
(t)
n=0
unde: an
– ponderea funcţiei fn
(valoare constantă)
fn
(t) – set predefinit de funcţii elementare
N – numărul maxim de funcţii elementare necesare pentru
exprimarea funcţiei x(t)

12. Set ortogonal de semnale elementare
(simple)
 Relatia de ortogonalitate intre functii (semnale)
elementare
t0+T C2
dacă m = n
∫ fm(t)*fn(t) dt=
t0 0 dacă n ≠ m
unde: fm şi fn - două funcţii elementare
C – norma (mărimea) funcţiei elementare
T – intervalul de ortogonalitate
t0 – momentul considerat pentru calcul
Un set de funcţii elementare este ortogonal dacă se
respectă proprietatea de ortogonalitate pentru oricare
două perechi de funcţii

13. Aproximarea unui semnal x(t) prin functii
elementare ortogonale
 Un set de funcţii elementare este ortogonal
dacă se respectă proprietatea de
ortogonalitate pentru oricare două perechi de
funcţii
t0+T t0+T N
∫ x(t)*fm(t) dt = ∫ (Σ an* fn(t))*fm(t) dt =
t0 t0
n=0
N t0+T
= Σ an ( ∫ fn(t)*fm(t)dt) = am* C2
, de unde rezultă
n=0
t0
t0+T
am = 1/C2
∫ x(t)*fm(t) dt
t0

14. Componenta spectrala a unui semnal
complex
 a0, a1,… an – amplitudinile componentelor
spectrale ale semnalului
a0
a1
a2
a3
a4
n
a5

15. Transformata Fourier discretă
 Set ortogonal de semnale trigonometrice:
 1/√2 , cos(n ωt), sin(n ωt), n = 0 .. N, ω=2π/T
 Se verifică relaţiile de ortogonalitate:
t0+T T/2, pentru n = m
∫ cos (m ωt)*cos (n ωt) dt =
t0 0, pentru n ≠ m
t0+T
∫ cos (m ωt)*sin (n ωt) dt = 0
t0

16. Analiza Fourier a unui semnal
 exprimarea semnalului ca o sumă ponderată de semnale
sinusoidale de forma:
∞ ∞
x(t) = C0 + Σ Cn cos(n ωt) + Σ Sn sin(n ωt)
n=1 n=1
t0+T
Cn = 2/T ∫ x(t)*cos (n ωt) dt
t0
t0+T
Sn = 2/T ∫ x(t)*sin (n ωt) dt
t0
t0+T
C0 =√2/T ∫ x(t) dt
t0

17. Transformata Fourier discretă a unui semnal
periodic x(t), de perioadă T
 forma trigonometrică a transformatei Fourier discrete
∞ ∞
F(t) = C0 + Σ Cn cos(n ωt) + Σ Sn sin(n ωt)
n=1 n=1
F(t)=x(t) x(t)
F(t)
t t
x(t) - semnal periodic x(t) – semnal aperiodic

18. Forma armonică a transformatei
Fourier discrete
 Perechile de termeni Sn sin(n ωt) şi Cn cos (n ωt) se pot exprima
printr-o singură funcţie de forma
An cos (n ωt + φn) unde:
 An
2
= Cn
2
+Sn
2
- reprezintă pătratul amplitudinii armonicii de
rang n, iar
 φn = - arctg Sn/Cn - reprezintă defazajul armonicii de rang n
unde: cos(ωt + φ1) – este componenta fundamentală de
frecvenţă f
cos(nωt + φn) – este armonica de rang n şi frecvenţă n*f
φn – este faza (unghiul de defazaj) al armonicii n
An – amplitudinea armonicii de rang n
∞
F(t) = A0 + Σ An cos(n ωt + φn)
n=1

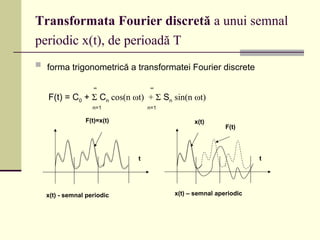
19. Forma complexă a transformatei Fourier
discrete
 În expresia de mai sus, cos(n ωt + φn) se poate considera ca parte reală a
numărului complex e j(n ωt + φn)
(de reamintit forma trigonometrică a unui număr
complex e jα
= cosα +jsinα). Astfel termenul n din sumă devine:
An cos(n ωt + φn) = Re [An e j(n ωt + φn)
] = Re [Anc e j(n ωt)
]
unde: Anc = An * e j(φn)
– este amplitudinea complexă a armonicii n
+∞
F(t) = 1/2 Σ Anc ej(n ωt)
-∞
∞
F(t) = A0 + Re Σ Anc e j(n ωt)
n=1

20. Exemple de transformate Fourier
pentru semnale simple
 pentru semnal constant:
x(t) = A
- transformata Fourier are numai componenta constantă
C0 = A, Cn=0, Sn=0, pt, n=1.. ∞
 pentru semnal sinusoidal:
x(t) = A sin (ω0t)
- transformata Fourier are numai componenta
fundamentală de pulsaţie ω0t
C0 = 0, Cn=0, S1=A, Sn=0, pt, n=2 .. ∞
ωt
A
ωtω0t
A

21. Exemple de transformate Fourier
pentru semnale simple
 semnal dreptunghiular:
A pentru t∈ [2kT, (2k+1)T)
x(t) =
-A pentru t∈ [ (2k+1)T, (2k+2)T)
+∞
x(t) = 2A/π Σ 1/(2k+1) * sin((2k+1) ωt)
k=0
- transformata Fourier conţine un număr infinit de
funcţii sinus; amplitudinea sinusurilor scade
asimptotic la 0, în raport cu pulsaţia
C0 = 0, Cn=0, S2k=0, S2k+1=2A/(2k+1)π
- O aproximare buna a semnalului dreptunghiular se
poate face cu primele 3 componente spectrale ω 2ω 3ω 4ω 5ω ω
S2k+1 =2A/(2k+1)π
Sn

22. Transformata Fourier pentru semnale
aperiodice (de tip impuls)
 Impuls – semnal aperiodic de durata limitata
 Exemple de semnale de tip impuls:
 semnal dreptunghiular singular
 impuls Dirac singular
 o semiperioadă a unui semnal sinusoidal
 Perioada semnalului “T” tinde la infinit
 Pulsatia ω tinde la 0 => distanta dintre componentele spectrale este
infinitezimal de mica
 In transformata Fourier coeficientii Anc devin o funcţie continuă de
variabilă jω
 Integrala care calculeaza coeficientii=>transformata Fourier continua:
 Transformata Fourier inversă permite generarea (reconstruirea) unui semnal pe
baza distribuţiei sale spectrale
∞
X(jω) = ∫ x(t) * e- jωt
dt
-∞
∞
x(t) = 1/2π ∫ X(jω) * e- jωt
dω
-∞

23. Proprietatile Transformatei Fourier
 Teorema întârzierii
F(x(t-t0)) = e-jωt0 X(jω)
 Teorema derivării
F( dx(t)/dt) ) = jω X(jω)
 Teorema integrării
F(∫ x(t)dt) ) = 1/jω * X(jω)
 Teorema convoluţiei
Convoluţia a două funcţii x(t) şi y(t) se defineşte în felul următor:
∞
x(t)○y(t) = ∫ x(τ)*y(t - τ) dτ
-∞
Convoluţia se utilizează frecvent pentru evaluarea efectului produs
de un sistem liniar asupra unui semnal complex.
∞
F [ (∫ x(τ)*y(t - τ) dτ ] = X(jω) *Y(jω)
-∞