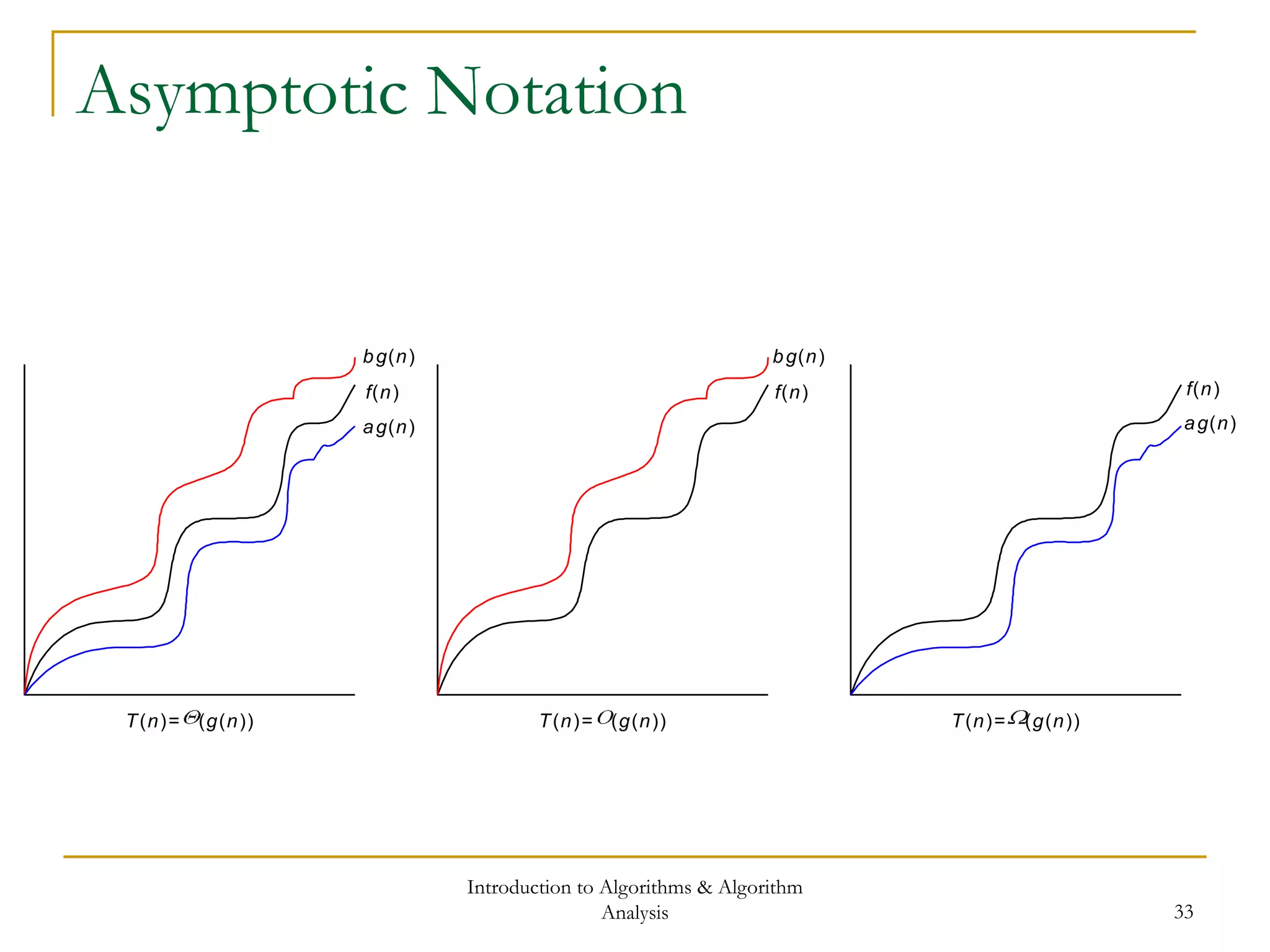
This document provides an introduction to algorithms and algorithm analysis. It defines what an algorithm is, provides examples, and discusses analyzing algorithms to determine their efficiency. Insertion sort and merge sort are presented as examples and their time complexities are analyzed. Asymptotic notation is introduced to describe an algorithm's order of growth and provide bounds on its running time. Key points covered include analyzing best-case and worst-case time complexities, using recurrences to model algorithms, and the properties of asymptotic notation. Homework problems are assigned from the textbook chapters.

1. Advanced Data Structures &
Algorithm Design
Introduction to Algorithms and Algorithm
Analysis

2. Introduction to Algorithms & Algorithm
Analysis 2
What is an Algorithm?
 Any well-defined computational procedure that takes
some value or set of values as input, and produces
some value or values as output; or
 A sequence of computational steps that transforms
the input into the output; or
 Tool for solving a well-specified computational
problem
 The problem specifies the relationship between input and
output
 The algorithm describes a procedure for achieving that
relationship

3. Introduction to Algorithms & Algorithm
Analysis 3
Algorithms: An Example
 The Sorting Problem
 The need to sort data arises frequently in practice
 Formally, the sorting problem is specified as:
 Input: A sequence of n numbers {a1, a2, …, an}
 Output: A permutation (reordering) {a1’, a2’, …, an’} of
the input sequence such that a1’ <= a2’ <= … <= an’
 That is, given the input sequence { 5, 7, 3, 2, 9
}, a sorting algorithm returns as output the
sequence { 2, 3, 5, 7, 9}
 This is one instance of the sorting problem

4. Introduction to Algorithms & Algorithm
Analysis 4
Correctness of Algorithms
 An algorithm is correct if for every input
instance, it halts with the correct output
 i.e., it solves the given computational problem
 Correctness isn't everything
 Incorrectness can be useful, if the error rate can
be controlled

5. Introduction to Algorithms & Algorithm
Analysis 5
Analyzing Algorithms
 To analyze an algorithm means to predict the
resources that an algorithm will require
 Why do we care about an algorithm’s
resource requirements?
 Resources are bounded – there isn’t an infinite
amount of time or space for an algorithm to
execute in
 What resources do we care about?
 Time (how long does it take)
 Space (how much memory does it use)

6. Introduction to Algorithms & Algorithm
Analysis 6
Analyzing Algorithms
 Analysis usually measures two forms of
complexity:
 Spatial Complexity: memory, communications
bandwidth
 Temporal Complexity: computational time

7. Introduction to Algorithms & Algorithm
Analysis 7
Analyzing Algorithms: An Example
 Two algorithms for solving the same problem
often differ dramatically in their efficiency
 Consider two sorting algorithms:
 Insertion sort takes time roughly equal to c1n2
 n is the number of items being sorted;
 c1 is a constant that does not depend on n
 Merge sort takes time roughly equal to c2nlog2n

8. Introduction to Algorithms & Algorithm
Analysis 8
Analyzing Algorithms: An Example
 What does this mean? Consider sorting
1,000,000 numbers on two different
computers
 Computer A uses insertion sort, and executes
1,000,000,000 instructions per second; we’ll
assume c1 = 2
 Computer B uses merge sort, and executes
10,000,000 instructions per second; we’ll assume
c2 = 50
 How long does it take?

9. Introduction to Algorithms & Algorithm
Analysis 9
Analyzing Algorithms: An Example
 Computer A:
 Computer B:
seconds2000
ns/secinstructio10
nsinstructio102
9
26
seconds100
ns/secinstructio10
nsinstructio10log1050
7
6
2
6

10. Introduction to Algorithms & Algorithm
Analysis 10
Insertion Sort
 Insertion sort is one method of solving the
sorting problem
 Conceptually, insertion sort works the way
many people sort playing cards:
 Start with one hand empty and the cards face
down
 Remove one card at a time from the table and
insert it into the correct position in the left hand

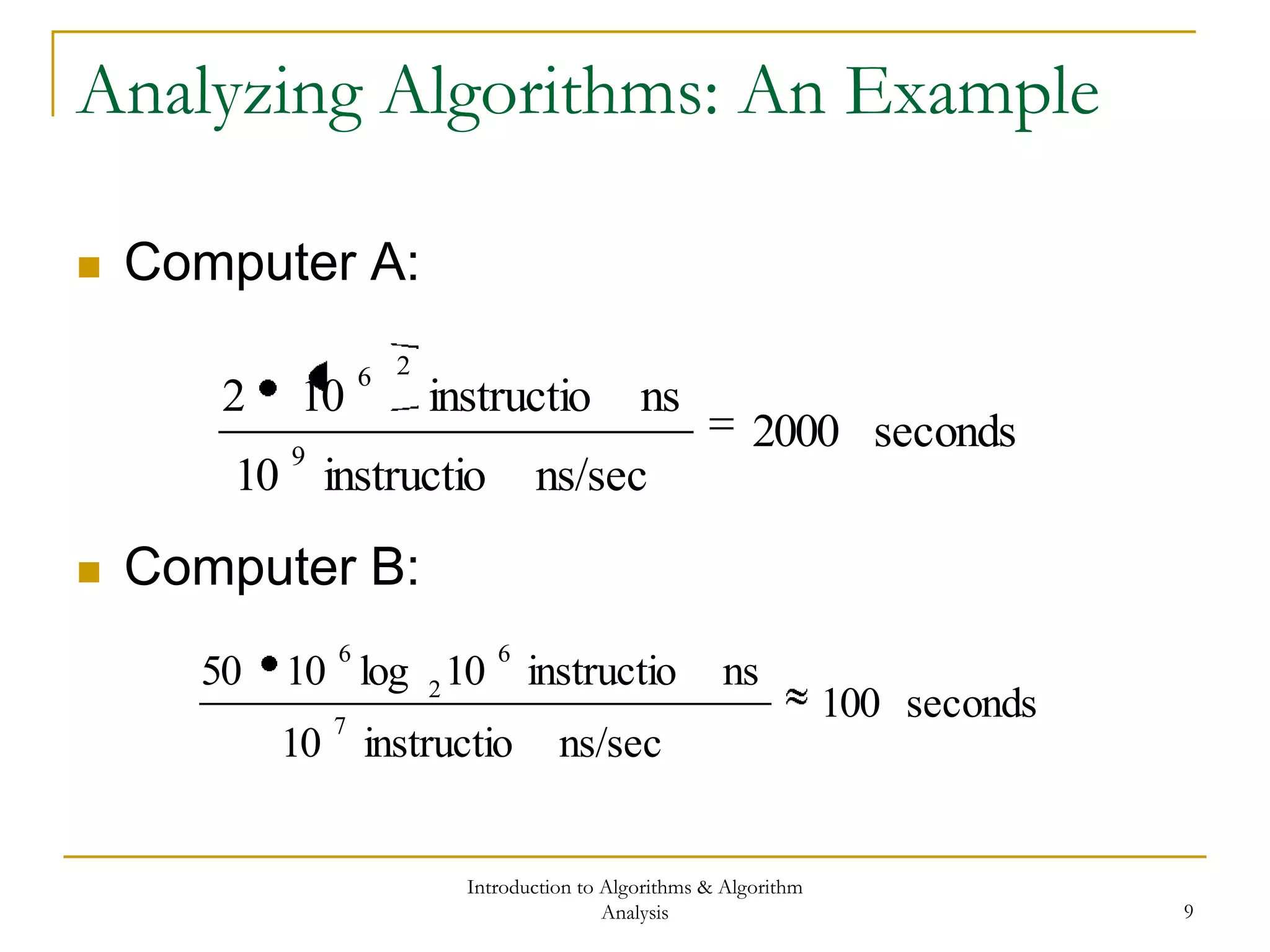
11. Introduction to Algorithms & Algorithm
Analysis 11
Insertion Sort: Algorithm
void InsertionSort(ArrayType A[], unsigned size)
{
for ( unsigned j = 1 ; j < size ; ++j )
{
ArrayType key = A[j];
int i = j-1;
while ( i >= 0 && A[i] > key )
{
A[i+1] = A[i];
--i;
}
A[i+1] = key;
}
}

12. Introduction to Algorithms & Algorithm
Analysis 12
Operation of Insertion Sort
5 2 4 6 1 3
5
2
4 6 1 3
52 4 6 1 3

13. Introduction to Algorithms & Algorithm
Analysis 13
Operation of Insertion Sort
52 4 6 1 3
52 4 6 1 3
52 4 61 3
52 4 61 3
52 4 61 3

14. Introduction to Algorithms & Algorithm
Analysis 14
Analysis of Insertion Sort
 How long does insertion sort take?
 Time varies based on:
 The size of the input
 How well sorted the input is to begin with
 What is “the size of the input”?
 May represent the number of items in the input, or
the number of bits being calculated
 May be represented by more than one number

15. Introduction to Algorithms & Algorithm
Analysis 15
Analysis of Insertion Sort
 What is “running time”?
 Running time is based on the number of steps
performed by the processor
 Different processors run at different speeds, so
time per step will vary between processors
 We will express times in terms of a constant cost
per step, ci

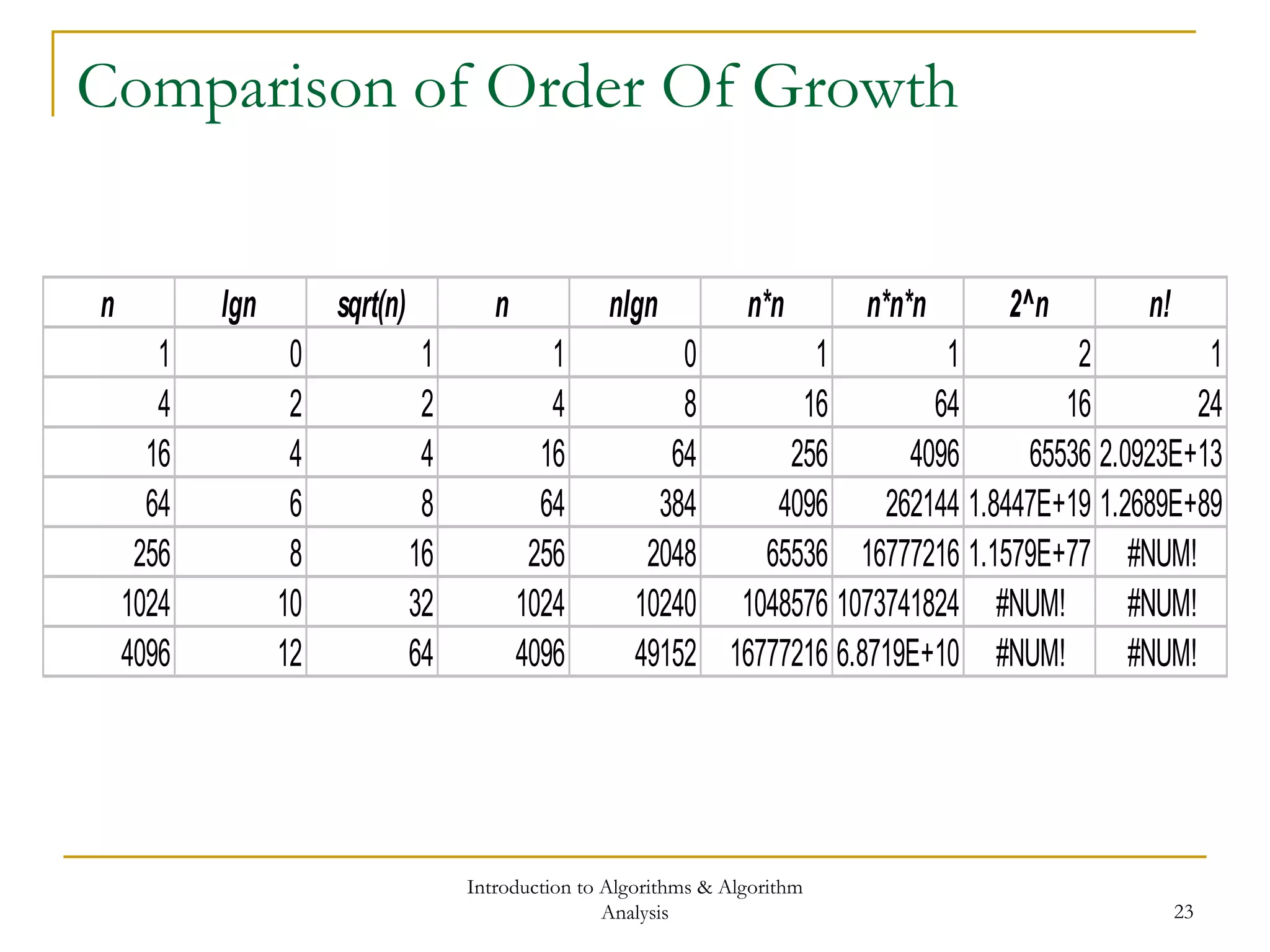
16. Introduction to Algorithms & Algorithm
Analysis 16
Analysis of Insertion Sort
 What is the “cost” of Insertion Sort?
 Total cost = the sum of the cost of each statement *
number of times statement is executed
Statem ent Cost Tim es
for ( unsigned j = 1 ; j < size ; ++j ) c1 n
ArrayType key = A[j]; c2 n-1
int i = j-1; c3 n-1
while ( i >= 0 && A[i] > key ) c4
n
j j
t
1
A[i+1] = A[i]; c5
n
j
t j1
)1(
--i; c6
n
j
t j1
)1(
A[i+1] = key; c7 n-1

17. Introduction to Algorithms & Algorithm
Analysis 17
Analysis of Insertion Sort
 In the best case, all tj = 1
 The inner loop only executes once, because the array is
already sorted
 In this case, T(n)=(c1+c2+c3+c4+c7)n-(c2+c3+c4+c7)
 Since all constants are unknown, we can as easily say that
T(n)=an+b, where a and b depend on the cost of each
statement
 So in the best case, the running time is a linear function of n
)1()1()()1()1()( 716514321
nctcctcncncncnT
n
j j
n
j j
 Total cost for insertion sort is:

18. Introduction to Algorithms & Algorithm
Analysis 18
Analysis of Insertion Sort
 In the worst case, tj=j, since every element must be
compared
 This occurs when the array is reverse sorted
 To solve this, we need the solve the summations:
)1()1()()1()1()( 716514321
nctcctcncncncnT
n
j j
n
j j
n
j
nn
j
1
1
2
)1(
n
j
nn
j
1
2
)1(
)1(

19. Introduction to Algorithms & Algorithm
Analysis 19
Analysis of Insertion Sort
 So, in the worst case:
)1(
2
)1(
)(1
2
)1(
)1()1()( 7654321
nc
nn
cc
nn
cncncncnT
)()(
2
1
2
)()( 74326547321
2
654
ccccnccccccc
n
cccnT
 We can say that T(n)=ax2+bx+c
 The running time in the worst case is therefore a
quadratic function of n
 In general, we are most interested in worst case
running time

20. Introduction to Algorithms & Algorithm
Analysis 20
Analysis of Insertion Sort
 Order of Growth
 Actual running time is not nearly as important as
the “order of growth” of the running time
 Order of growth of the running time is how the running
time changes as the size of the input changes
 Provides a concrete method of comparing alternative
algorithms

21. Introduction to Algorithms & Algorithm
Analysis 21
Analysis of Insertion Sort
 Order of Growth
 Order of growth is typically easier to compute than
exact running time
 In general, we are most interested in the highest order
terms of the running time
 Lower order terms become insignificant as the input size
grows larger
 We can also ignore leading coefficients
 constant factors are not as significant as growth rate in
determining computational efficiency

22. Introduction to Algorithms & Algorithm
Analysis 22
Analysis of Insertion Sort
 Example of Order of Growth:
 Best case:
 Linear running time: T(n)=an+b
 The order of growth is O(n)
 This representation (O(n)) is called asymptotic notation
 Worst case:
 Quadratic running time: T(n)=an2+bn+c
 The order of growth is (O(n2))
 Order of growth provides us a means of comparing
the efficiency of algorithms
 Algorithms with lower worst-case order of growth are
usually considered to be more efficient

23. Introduction to Algorithms & Algorithm
Analysis 23
Comparison of Order Of Growth
n lgn sqrt(n) n nlgn n*n n*n*n 2^n n!
1 0 1 1 0 1 1 2 1
4 2 2 4 8 16 64 16 24
16 4 4 16 64 256 4096 65536 2.0923E+13
64 6 8 64 384 4096 262144 1.8447E+19 1.2689E+89
256 8 16 256 2048 65536 16777216 1.1579E+77 #NUM!
1024 10 32 1024 10240 1048576 1073741824 #NUM! #NUM!
4096 12 64 4096 49152 16777216 6.8719E+10 #NUM! #NUM!

24. Introduction to Algorithms & Algorithm
Analysis 24
Designing Algorithms
 Insertion sort is typical of an incremental
approach to algorithm design
 The input is processed in equally sized
increments
 An alternative approach is divide-and-
conquer
 The input is recursively divided and processed in
smaller, similar chunks

25. Introduction to Algorithms & Algorithm
Analysis 25
Divide and Conquer
 Divide and Conquer is a recursive approach
to algorithm design
 Consists of three steps at each level of
recursion:
 Divide the problem into smaller, similar
subproblems
 Conquer the subproblems by solving them
recursively
 Combine the solutions to the subproblems into
the solution to the original problem

26. Introduction to Algorithms & Algorithm
Analysis 26
The Merge Sort
9 7 4 5 2 1 6 3 8 0
9 7 4 5 2 1 6 3 8 0
974 52 1 63 80
0 1 2 3 4 5 6 7 8 9

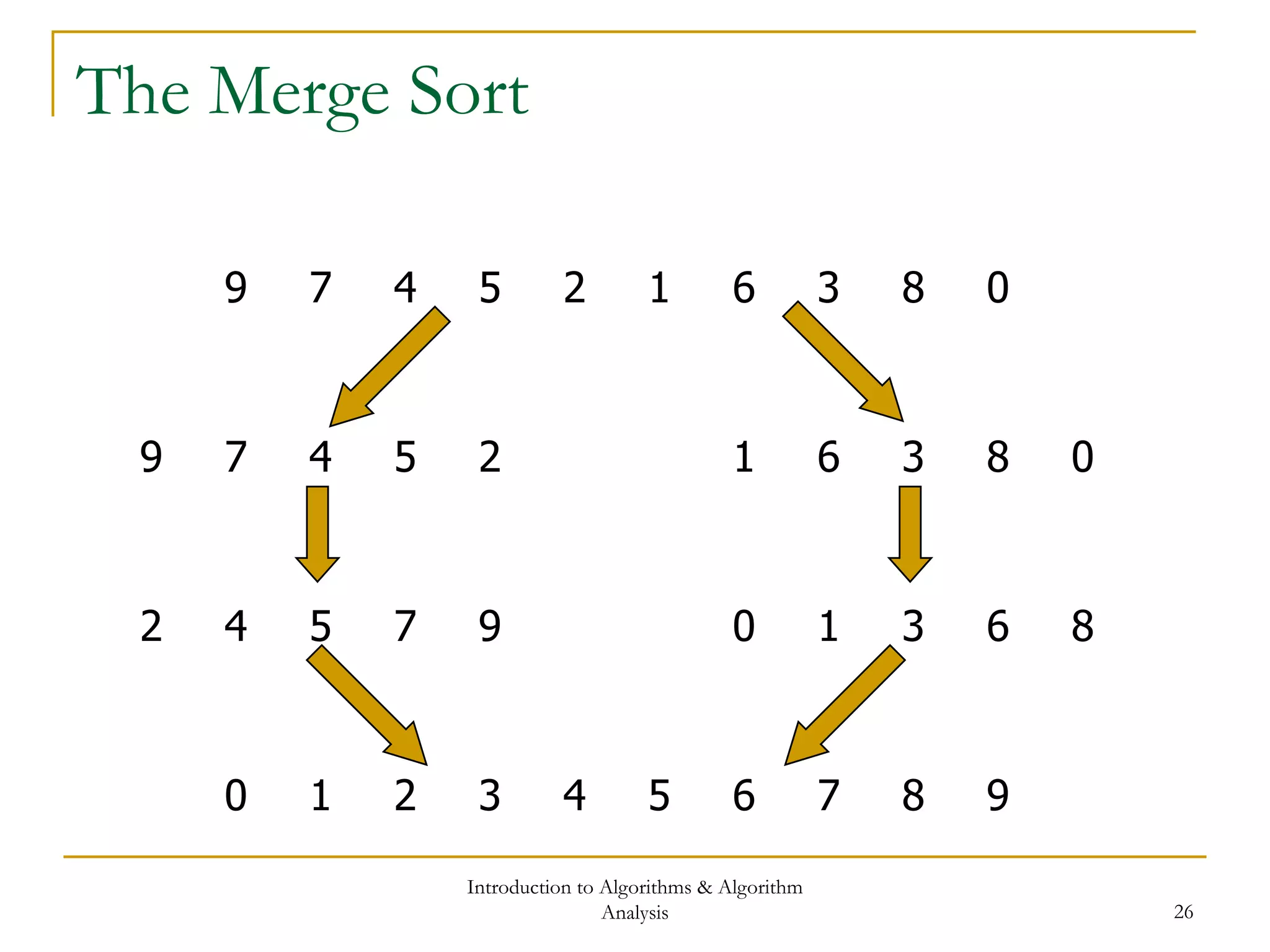
27. Introduction to Algorithms & Algorithm
Analysis 27
The Merge Sort
void MergeSort(ArrayType A[], int p, int r)
{
if ( p < r )
{
int q = (p+r)/2; // Divide
MergeSort(A, p, q); // Conquer left
MergeSort(A, q+1, r); // Conquer right
Merge(A, p, q, r); // Combine
}
}

28. Introduction to Algorithms & Algorithm
Analysis 28
Analysis of Merge Sort
 How do we describe the running time of
Merge Sort?
 We must derive a recurrence
 A recurrence describes the overall running time of
an algorithm on a problem of size n in terms of the
running time on smaller inputs

29. Introduction to Algorithms & Algorithm
Analysis 29
Analysis of Merge Sort
 What is the recurrence for Merge Sort?
 Dividing always takes the same time; it is constant
(represented as O(1))
 Conquering occurs twice, on an input half the original size
 Conquering therefore takes 2T(n/2)
 Merge() is not presented, but should be linear (O(n))
 This leads to a total running time of T(n) =
2T(n/2)+O(n)+O(1)
 O(1) is constant, and can be dropped
 This is an infinite recurrence - when does it stop?
 When the input size reaches 1

30. Introduction to Algorithms & Algorithm
Analysis 30
Analysis of Merge Sort
 So, the total running time is shown as the
following recurrence:
 We shall show later in the course that the
order of growth for this recurrence is
O(nlog2n)
1if)()2/(2
1if)1(
)(
nnOnT
nO
nT

31. Introduction to Algorithms & Algorithm
Analysis 31
Asymptotic Notation
 Asymptotic notation provides a means of
bounding the running time of an algorithm
 Upper bounds signify worst-case running times
 E.g., if T(n) has an upper bound of g(n), this means that
the running time of T(n) is at most cg(n)
 Lower bounds signify best-case running times

32. Introduction to Algorithms & Algorithm
Analysis 32
Asymptotic Notation
 There are three basic asymptotic notations:
 O-notation: denotes the upper bound of an
expression
 -notation: denotes the lower bound of an
expression
 -notation: denotes both upper and lower
bounds of an expression

33. Introduction to Algorithms & Algorithm
Analysis 33
Asymptotic Notation
f(n)
ag(n)
bg(n)
f(n)
bg(n)
f(n)
ag(n)
T(n)= (g(n)) T(n)= (g(n)) T(n)= (g(n))

34. Introduction to Algorithms & Algorithm
Analysis 34
Asymptotic Notation
 Why do we use asymptotic notation?
 Reduces clutter by eliminating constant factors
and lower-order terms
 E.g., 2n2 + 3n + 1 = 2n2 + O(n) = O(n2)
 We are interested in comparing algorithms
 Actual running times are very hard to compute, and
compare
 Bounds are easier to compute and provide a more
realistic basis for comparison
 We can always go back and compute actual running
times if we need them

35. Introduction to Algorithms & Algorithm
Analysis 35
Asymptotic Notation
 Asymptotic notation of running times exhibits
some important mathematical properties:
 Transitivity: If f(n) = O(g(n)) and g(n) = O(h(n))
then f(n) = O(h(n))
 Reflexivity: f(n) = O(f(n))

36. Introduction to Algorithms & Algorithm
Analysis 36
Homework
 Reading: Chapters 1 & 2
 Exercises:
 1.1: 1, 2, 3
 1.2: 2, 5
 1.3: 1, 2, 4, 5, 6
 2.1: 2
 Problems:
 1-1, 2-1, 2-4