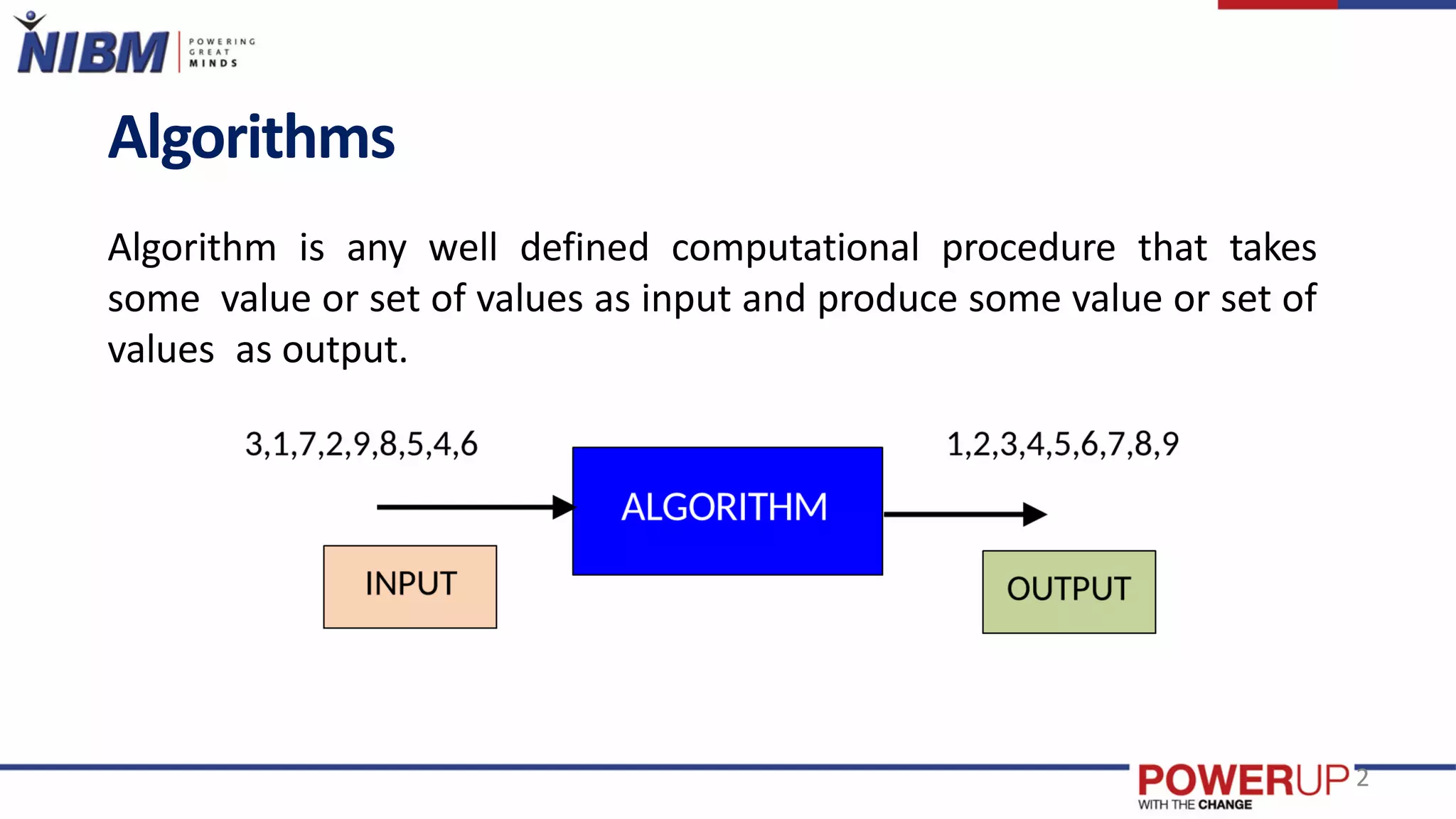
This document discusses complexity analysis of algorithms. It defines an algorithm and lists properties like being correct, unambiguous, terminating, and simple. It describes common algorithm design techniques like divide and conquer, dynamic programming, greedy method, and backtracking. It compares divide and conquer with dynamic programming. It discusses algorithm analysis in terms of time and space complexity to predict resource usage and compare algorithms. It introduces asymptotic notations like Big-O notation to describe upper bounds of algorithms as input size increases.

1. Complexity Analysis of
Algorithms

2. Algorithms
Algorithm is any well defined computational procedure that takes
some value or set of values as input and produce some value or set of
values as output.
2

3. Properties of an Algorithm
 Be correct.
 Be unambiguous.
 Give the correct solution for all cases.
 Be simple.
 It must terminate.
3

4. Designing of an Algorithm
Divide and Conquer
• Works by recursively breaking down a problem into
two or more sub-problems of the same (or related)
type, until these become simple enough to be solved
directly.
• The solutions to the sub-problems are then combined
to give a solution to the original problem
4

5. Designing of an Algorithm (Cont.)
Dynamic Programming
 It is both a mathematical optimization method
and a computerprogramming method.
 Saving results of sub-problems so that they do not need to
be recomputed. And can be used in solving other sub-
problems.
5

6. Divide & conquer vs Dynamic programming
6
1.The D&C involves three steps at each level of the recursion:
* Divide the problem into a number of sub problems.
* Conquer the sub problems by solving them recursively. If the sub problem sizes are
small enough, however, just solve the sub problems in a straightforward manner.
* Combine the solutions to the sub problems into the solution for the original
problem.
2.D&C does more work on the sub-problems and hence has more time
consumption.
3.In D&C the sub problems are independent of each other. Example:
Merge Sort, Binary Search

7. Divide & conquer vs Dynamic programming
 Dynamic Programming solves the sub problems only once and then
stores it in the table.
 In DP the sub-problems are not independent.
Example : Matrix chain multiplication
7

8. Designing of an Algorithm (Cont.)
The Greedy Method
Follows the problem-solving heuristic of making the locally optimal
choice at each stage with the hope of finding a global optimum.
8

9. Designing of an Algorithm (Cont.)
Backtracking
The Backtracking is a general algorithmic technique that considers
searching every possible combination in order to solve an
optimization problem
“systematically searches for a solution to a problem among all
available option”
9

10. Advantages of above methods
 Provide a template.
 Translation to data structures is easy.
 The temporal and spatial requirements can be precisely analyzed.
10

11. Algorithm as Technology
 Different algorithms devised to solve the same problem often
differ dramatically in their efficiency.
 These differences can be much more significant than
differences due to hardware and software.
11

12. For an example, let us pit a faster computer (computer A)
running insertion sort against a slower computer
(computer B) running merge sort. They each must sort an
array of 10 million numbers(if numbers are 8byte integers
:- 80 megabytes). Suppose that computer A executes 10
billion instructions per second and computer B executes
only 10 million instructions per second.
 Insertion sort (IS) takes time 2n2 to sort n numbers.
 Merge sort (MS) takes time 50n lg n
12

13. Algorithm as .. (contd. )
 Assume CPU A runs IS, and CPU B runs MS
 A takes:
 B takes:
1010instructions/sec
2(107 )2 instructions  20000seconds(5.5hours)
107instructions/sec
13
50 107 lg107 instructions 
1163seconds( 20minutes)

14. Algorithm as .. (contd. )
 But computer A is 1000 times faster than
computer B in raw computing power.
 In general, as the problem size increases, so does the relative
advantage of merge sort.
14

15. Analysis of Algorithms
Idea is to predict the resource usage.
• Memory
• Logic Gates
• Computational Time(***)
Why do we need an analysis?
• To compare
• Predict the growth of run time
15

16. Analysis of Algorithms
 Study of computer program performance and resource usage.
 Efficiency measure:
- Speed: How long an algorithm takes to produce results
- Space requirement
- Memory requirement
 Use the same computation model for the analyzed algorithms
16

17. Analysis of Algorithms
 In general, the time taken by an algorithm grows with the size of the
input.
 Input size: depends on problems being studied
(e.g. #elements, #nodes, #links).
 Running time on a particular input: #of primitive operations or steps
executed.
17

18. Analysis of Algorithms(Contd.)
 Space Complexity
 Time Complexity
18

19.  Methods for time complexity analysis.
 Select one or more operations such as add, multiply and
compare.
 Operation count: Omits accounting for the time spent on all
but the chosen operations.
Operation count
19

20. int sum = 0;
20
// 1time
}
T(n) = 3n+3
int i = 0; // 1 time
while (i < n){ // n+1 times
sum++;
i++;
// ntimes
// ntimes int sum = 0; // 1time
int i = 1;
while (i < n) {
// 1 time
// n times
sum++; // n-1times
i++; // n-1 times
}
T(n) =3n
Examples

21. Q1
Activity
21
int i = 0;
While(i<=10)
{
sum = sum+1;
i++;
}
Q2
int i = 0;
While(i<=n)
{
sum = sum+1;
i++;
}
Q3
int i = 1;
While(i<=n)
{
sum = sum+1;
i++;
}

22. Operation count (Cont.)
1 assignment
n+1comparrisions
n additions
n additions
22
int sum = 0; 1 assignmant
for (int i = 0; i < n; i++ )
{
sum++;
}
T(n) = 3n+3

23. Worst, Best and Average case
Running time will depend on the chosen instance
characteristics.
• Best case: minimum number of steps taken onany
instance of size n.
• Worst case: maximum number of steps taken onany
instance of size n.
• Average case: An average number of steps takenon any
instance of size n.
23

24. Worst, Best and Average case
Average case
24
worst case
Best case
Input Size
# of steps

25. Step Count (RAM Model)
 Random Access Machine
 Assume a generic one processor.
 Instructions are executed one after another, with no concurrent
operations.
 +,-,=,it takes exactly one step.
 Each memory access takes exactly 1 step.
 Running Time = Sum of the steps.
25

26. n  100
26
n  n +100
Print n
1step
2steps
1step
4steps
RAM Model Analysis
sum  0
for i  0 to n
sum  sum A[i]
Steps 6n+9
1 assignment
n+2 assignments
n+2 comparisons
n+1 additions
n+1 assignments
n+1 additions
n+1 memory accesses

27. Problems with RAM Model
 Differ number of steps with different architecture.
 It is difficult to count the exact number of steps in the
algorithm.
ex: See the insertion sort
27

28. Asymptotic Notations
Suppose that programs A and B perform the same task.
Assume that one person has determined the step counts of
these programs to be t A(n)=2n2+3n and t B(n)=13n.
 Which program is the faster one ?
 What is the answer if the step count of the program B is
2n+n2 ?
28

29. Graphs of functions
29

30. Asymptotic Notations
There are three notations.
O - Notation
 - Notation
 - Notation
30

31. Big O -Notation
 Introduced by Paul Bechman in 1892.
 We use Big O-notation to give an upper bound on afunction.
Definition:
Eg: What is the big O value of f(n)=2n + 6?
31

32. Big O -Notation
32

33. Big O -Notation
Find the Big O value for following fragment of code.
33
for i  1 to n
for j  1 to i
Print j
O(n2)

34. Big O -Notation
Assignment (s 1)
Addition (s+1)
Multiplication (s*2)
Comparison (S<10)
34
O(1)

35. Big O -Notation
Find the Bog O value for the following functions.
(i) T(n)= 3 +5n + 3n2
(ii) T(n)= 2n + n2 +8n +7
(iii)T(n)= n + logn +6
35

36. Int i =10;
While(i>0)
{
print i;
i--;
}
Int i =n;
While(i>0)
{
print i ;
i--;
}
int I, j;
For(int I =0; I<10; i++)
{
for (int j=0; j<=10; j++)
{
print i + j;
}
}
Int k =0;
While(k<=n+1)
{
print k;
k++;
}
Find the time complexity and Big(O) for each of the following code segment.
36

37. 44