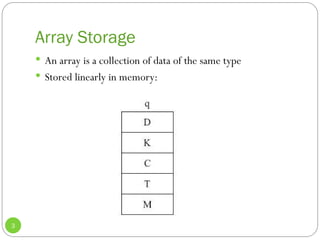
The document discusses arrays as a fundamental data structure, outlining key operations such as insertion, searching, and deletion, specifically focusing on ordered and unordered arrays. It highlights the efficiency of binary search on ordered arrays compared to linear search, and also explores object storage within arrays, big-oh notation for algorithm efficiency, and trade-offs between unordered and ordered arrays. Additionally, it gives insights into implementation strategies and the appendices indicate advanced data structures that offer improved performance for various operations.



![Defining a Java Array
5
Say, of 100 integers:
int[] intArray;
intArray = new int[100];
We can combine these statements:
Or, change the [] to after the variable name
What do the [] signify?](https://image.slidesharecdn.com/ch02-241114023430-a08c8c96/85/Chapter-three-data-structure-and-algorithms-qaybta-quee-5-320.jpg)
![We said an array was a reference…
6
That means if we do this:
int[] intArray;
intArray = new int[100];
What exactly does intArray contain? Let’s look internally.](https://image.slidesharecdn.com/ch02-241114023430-a08c8c96/85/Chapter-three-data-structure-and-algorithms-qaybta-quee-6-320.jpg)
![The Size
7
Size of an array cannot change once it’s been declared:
intArray = new int[100];
But, one nice thing is that arrays are objects. So you can
access its size easily:
int arrayLength = intArray.length;
Getting an array size is difficult in many other languages](https://image.slidesharecdn.com/ch02-241114023430-a08c8c96/85/Chapter-three-data-structure-and-algorithms-qaybta-quee-7-320.jpg)
![Access
8
Done by using an index number in square brackets:
int temp = intArray[3]; // Gets 4th
element
intArray[7] = 66; // Sets 8th
element
How do we access the last element of the array, if we don’t
remember its size?
What range of indices will generate the IndexOutOfBounds
exception?
The index is an offset. Let’s look at why.](https://image.slidesharecdn.com/ch02-241114023430-a08c8c96/85/Chapter-three-data-structure-and-algorithms-qaybta-quee-8-320.jpg)
![Initialization
9
What do the elements of this array contain:
int[] intArray = new int[100];
How about this one:
BankAccount[] myAccounts = new BankAccount[100];
What happens if we attempt to access one of these values?
int[] intArray = {0, 3, 6, 9, 12, 15, 18, 21, 24,
27};
Automatically determines the size
Can do this with primitives or objects](https://image.slidesharecdn.com/ch02-241114023430-a08c8c96/85/Chapter-three-data-structure-and-algorithms-qaybta-quee-9-320.jpg)







![Note what this can save!
18
Let’s take a simple case, where we search for an item in a
100-element array:
int[] arr = {1,2,3,4,5,6,…..,100}
For an unordered array where we must use linear search,
how many comparisons on average must we perform?
How about for binary search on an ordered array? Let’s look
for the element 33.](https://image.slidesharecdn.com/ch02-241114023430-a08c8c96/85/Chapter-three-data-structure-and-algorithms-qaybta-quee-18-320.jpg)













![Example: Insertion into Unordered
Array
32
Suppose we just insert at the next available position:
Position is a[nElems]
Increment nElems
Both of these operations are independent of the size of the
array n.
So they take some time, K, which is not a function of n
We say this is O(1), or constant time
Meaning that the runtime is proportional to 1.](https://image.slidesharecdn.com/ch02-241114023430-a08c8c96/85/Chapter-three-data-structure-and-algorithms-qaybta-quee-32-320.jpg)








