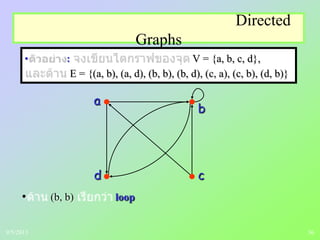
(1) The document discusses binary relations and concepts such as ordered pairs, reflexive relations, symmetric relations, inverse relations, and representing relations using matrices. (2) It also covers topics like equivalence relations, equivalence classes, and partitioning a set based on an equivalence relation. (3) Examples are provided to illustrate key concepts like inverse relations, representing relations as directed graphs, and determining equivalence classes.

1. 1
Chapter 4
Relations
9/5/2013

2. 2
Relations
•
A B, ordered
pairs A
B
binary relation
• : A B binary relation A
B A B
• binary relation R R A B
aRb (a, b) R a R b
(a, b) R
A B = {a, b}
R = {( , a) , ( , b) , ( , a) , ( , b) }9/5/2013

3. 3
Relations
• (a, b) R a
b R
• : P , C
, D
•P = { , , , },
•C = { , , }
•D = {( , ), ( , ),
( , ), ( , )}
•
9/5/2013

4. 4
(Complementary Relations)
• R:A B binary relation
R :≡ {(a,b) | (a,b) R}
• , R:A B, R,
binary relation
R :≡ {(a,b) | (a,b) R} = (A B) − R
• R
U = A B
• R R < = {(a,b) |
a<b)}
: < = {(a,b) | (a,b) <} = {(a,b) | ¬(a<b)} = ≥
9/5/2013

5. 5
(Inverse
Relations)
• R:A B
R−1:B A
R−1 :≡ {(b, a) | (a,b) R}
, <−1 = {(b, a) | a<b} = {(b, a) | b>a} = >
• , R: →
a R b a b R :≡ {(a, b) | a b}
:
b R−1 a b a R−1 :≡ {(b, a) | b
a }
9/5/2013

6. 6
(Inverse
Relations)
Q: R N : xRy y = x 2
R :≡ {(x, y) | y = x 2} R -1
?
A: xRy y = x 2
R R -1 :
:
yR -1x y = x 2 R−1 :≡ {(y, x) | y = x
2}
xR -1y x = y 2 R−1 :≡ {(x, y) | x = y
2}
xR -1y y = ± x R−1 :≡ {(x, y) | y =9/5/2013

7. 7
Example
• R={(a,b) | a b}
• R-1 ={(b,a) | a b}
={(a,b) | b a}
• S={(x,y) R R | y=(x+1)/3}
• S-1 ={(y,x) R R | y=(x+1)/3}
={(x,y) R R | x=(y+1)/3}
={(x,y) R R | y=3x-1}
9/5/2013

8. 8
• A
A
• “<”
N
• identity relation IA A
{(a,a)|a A}
• : A = {1, 2, 3, 4}
R = {(a, b) | a < b} ?
•Solution: R = {(1, 2),
(1, 3), (1, 4), (2, 3),
(2, 4), (3, 4)}
1 1
2
3
4
2
3
4
9/5/2013

9. 9
•
A n ?
• A A A
• A A ?
• n2 A A, (=
A) A A ?
• m 2m
A A 2n2
•Answer: A
2n2
9/5/2013

10. 10
• : R A
reflexive (a, a) R
a A
• U =
• :
– < reflexive x < x ,
(x, x) R
– ≥ :≡ {(a,b) | a≥b} reflexive (x, x)
R
• {1, 2, 3, 4} reflexive
?
•R = {(1, 1), (2, 2), (2, 3), (3, 3), (4, 4)} Yes
•R = {(1, 1), (2, 2), (3, 3)} No
• : A
irreflexive (a, a) R a A
: < irreflexive9/5/2013

11. 11
Symmetry & Antisymmetry
• R A
symmetric
R = R−1, (a,b) R ↔ (b,a) R
– , = ( ) symmetric x = y y
= x x y <
symmetric
– “ ” symmetric, “ ”
• R
antisymmetric
a≠b, (a,b) R → (b,a) R
– : < antisymmetric, “ ”
• R A
asymmetric a,b A, (a,b) R9/5/2013

12. 12
• {1, 2, 3, 4}
symmetric, antisymmetric, asymmetric?
•R = {(1, 1), (1, 2), (2, 1), (3, 3), (4, 4)} symmetric
•R = {(1, 1)} sym. and
antisym.
•R = {(1, 3), (3, 2), (2, 1)} antisym. and
asym.
•R = {(4, 4), (3, 3), (1, 4)} antisym.
9/5/2013

13. 13
: R transitive
( a,b,c) (a,b) R (b,c) R → (a,c) R
• intransitive
:
– “ ” transitive
– “ ” intransitive
– = < > transitive
• {1, 2, 3, 4} transitive ?
•R = {(1, 1), (1, 2), (2, 2), (2, 1), (3, 3)} Yes
•R = {(1, 3), (3, 2), (2, 1)} No
•R = {(2, 4), (4, 3), (2, 3), (4, 1)} No
9/5/2013

14. 14
Exercise
• A={1,2,3,4} R,S,T,U
A
• R={(1,3), (3,4)}
• S={(1,1), (2,2), (3,3), (2,3), (3,2), (1,4)}
• T={(1,1), (2,2), (1,2), (2,1), (3,3), (4,4)}
• U={(1,1), (2,2), (3,3), (2,3), (3,2), (1,4),
(4,2), (1,2),(1,3)}
9/5/2013

15. 15
Answer
• R Irreflexive, Antisymmetric
Asymmetric
• S Transitive
• T Reflexive, Symmetric,
Transitive
• U
9/5/2013

16. 16
Composite
Relations
• R:A B, S:B C
SR R S :
SR = {(a,c) | b: aRb bSc}
• Rn R A
R0 :≡ IA ; Rn+1 :≡ RRn n≥0
IA = {(x,x)| x A}
R−n :≡ (R−1)n
9/5/2013

17. 17
Composite
Relations
: D S A = {1, 2, 3,
4}
D = {(a, b) | b = 5 - a} “b (5 – a)”
S = {(a, b) | a < b} “a b”
D = {(1, 4), (2, 3), (3, 2), (4, 1)}
S = {(1, 2), (1, 3), (1, 4), (2, 3), (2, 4), (3, 4)}
S D =
Q: R N : xRy y =
x2
S N : xSy y = x 3
S  R ?
A:
S  R xSRy y = x 6 (
{(2, 4), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)}
9/5/2013

18. 18
Q: R1 R2
R2  R1 :
1 1 1 1
2 2 2 2
3 3 3 3
4 4 4
5 5R1 R2
9/5/2013

19. 19
1 1 1
2 2 2
3 3 3
4 4
5
A:
1:
1 1
2 2
3 3
4
R1 R2
R2  R19/5/2013

20. 20
1 1 1
2 2 2
3 3 3
4 4
5
A:
1:
1 1
2 2
3 3
4 R2  R1
R1 R2
9/5/2013

21. 21
1 1 1
2 2 2
3 3 3
4 4
5
A:
1:
1 1
2 2
3 3
4 R2  R1
R1 R2
9/5/2013

22. 22
1 1 1
2 2 2
3 3 3
4 4
5
A:
1:
1 1
2 2
3 3
4 R2  R1
R1 R2
9/5/2013

23. 23
1 1 1
2 2 2
3 3 3
4 4
5
A:
1:
1 1
2 2
3 3
4 R2  R1
R1 R2
R2  R1=
{(4,1),(4,2),(4,3)}
9/5/2013

24. 24
• : R A
Rn R n
• : R A
(a,b) R (b, c) R, (a, c) R a, b,
c A
• R
(a, c) R
R R R
R, R R R
• R R R
R (R R) R R,9/5/2013

25. 25
Representing
Relations)
• :
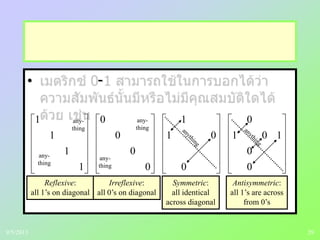
- Zero-one matrices
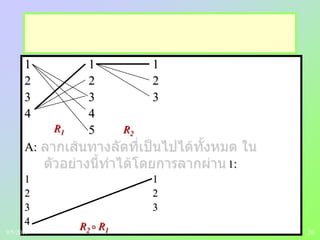
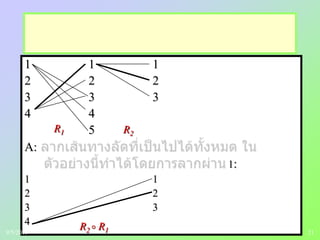
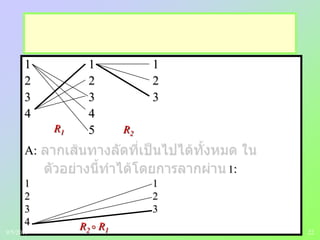
Directed graphs
• R
A = {a1, a2, …, am} B ={b1, b2, …, bn}, R
MR = [mij]
mij = 1, (ai, bj) R,
mij = 0, (ai, bj) R
•
9/5/2013

26. 26
• : R
{1, 2, 3} {1, 2} R
R = {(2, 1), (3, 1), (3, 2)} ?
• : MR
11
01
00
RM
9/5/2013

27. 27
• (
A A)
square matrices
•
Mref
1
.
.
.
1
1
Mref
9/5/2013

28. 28
•
MR = (MR)t
1101
1001
0010
1101
RM
0011
0011
0011
0011
RM
9/5/2013

29. 29
• -
0
0
101
0
0
01
1
0
0
0
0
1
1
1
1
Reflexive:
all 1‟s on diagonal
Irreflexive:
all 0‟s on diagonal
Symmetric:
all identical
across diagonal
Antisymmetric:
all 1‟s are across
from 0‟s
any-
thing
any-
thing
any-
thing
any-
thing
9/5/2013

30. 30
• : R S
MR MS
011
111
101
SRSR MMM
001
110
101
SM
• R S R S?
:
000
000
101
SRSR MMM
010
001
101
RM
9/5/2013

31. 31
• A = [aij] - m k
B = [bij] - k n
• Boolean product A B,
AB m n
i j [cij]
cij = (ai1 b1j) (ai2 b2j) … (aik bkj)
cij = 1 (ain bnj) = 1 n
(ain bnj) cij
= 09/5/2013

32. 32
• - MA = [aij], MB = [bij] MC = [cij]
A, B, C,
• MC = MAMB
cij = 1 (ain bnj) = 1
n
(ain bnj) cij = 0
C (xi, zj) yn
(xi, yn) A (yn, zj)
B
• C = B A (C A9/5/2013

33. 33
• B A
:
MB A = MAMB
•
A B
A Boolean product
B
•
:
[n]
9/5/2013

34. 34
• : R2
R
001
110
010
RM
: R2
010
111
110
]2[
2 RR
MM
9/5/2013

35. 35
Directed
Graphs
• directed graph) digraph)
G=(VG,EG) VG EG VG VG
R:A B
GR=(VG=A B, EG=R)
100
010
011
Mark
Fred
Joe
SallyMarySusan
R MR: R
GR: Joe
Fred
Mark
Susan
Mary
Sally
VG
EG
9/5/2013

36. 36
Directed
Graphs
• : V = {a, b, c, d},
E = {(a, b), (a, d), (b, b), (b, d), (c, a), (c, b), (d, b)}
a
b
cd
• (b, b) loop
9/5/2013

37. 37
Reflexive,
Symmetric
Directed Graphs






Reflexive: Irreflexive: Symmetric:
 
Antisymmetric:
 

asymmetric
antisymmetric
reflexive
irreflexive
9/5/2013

38. 38
(Equivalence
Relations)
•
• : A
(Reflexive)
(Symmetric) (Transitive)
•
R
9/5/2013

39. 39
(Equivalence Relations)
• : R
aRb l(a) = l(b),
l(x) x
R ?
• :
• R l(a) = l(a)
aRa a
• R l(a) = l(b)
l(b) = l(a)
aRb bRa
• R l(a) = l(b)
l(b) = l(c),
9/5/2013

40. 40
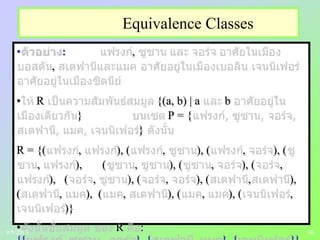
Equivalence Classes
• : R A
a
A a
• a R
[a]R [a]R :≡ { b | aRb }
•
a [a]
• b [a]R, b representative
9/5/2013

41. 41
Equivalence Classes
:
mouse,
[mouse] ?
: [mouse]
[mouse] ={horse, table, white,…}
„horse‟
9/5/2013

42. 42
Equivalence
Classes
• “ a b ”
– [a] =
a
• “ a b ”
– [a] = {a, −a}
• “ a b (
, a − b Z)”
– [a] = {…, a−2, a−1, a, a+1, a+2, …}
• “ a b
m ” ( m>1)
– [a] = {…, a−2m, a−m, a, a+m, a+2m, …}9/5/2013

43. 43
Equivalence Classes
: R A
:
• aRb
• [a] = [b]
• [a] [b]
: partition S
S
union
S Ai i I
S
(i) Ai i I
(ii) Ai Aj = , i j
(iii) A = S9/5/2013

44. 44
Partition
• : S {u, m, b, r, o, c, k,
s}
partition S
?
{{m, o, c, k}, {r, u, b, s}} yes
{{c, o, m, b}, {u, s}, {r}} no ( k)
{{b, r, o, c, k}, {m, u, s, t}} no (t S)
{{u, m, b, r, o, c, k, s}} yes
{{b, o, o, k}, {r, u, m}, {c, s}} yes ({b,o,o,k} = {b,o,k})
{{u, m, b}, {r, o, c, k, s}, } no ( )
9/5/2013

45. 45
Equivalence Classes
• : R S
R
partition S
{Ai | i I} S
R Ai, i I,
• R
S S
S
9/5/2013

46. 46
Equivalence Classes
• : ,
,
• R {(a, b) | a b
} P = {
}
R = {( , ), ( , ), ( , ), (
, ), ( , ), ( , ), ( ,
), ( , ), ( , ), ( , ),
( , ), ( , ), ( , ), ( ,
)}
• R :9/5/2013

47. 47
Equivalence Classes
• : R
{(a, b) | a b (mod 3)}
R (a, b) | a
b }
• R ?
• R
• R ?
{{…, -6, -3, 0, 3, 6, …},
{…, -5, -2, 1, 4, 7, …},
{…, -4, -1, 2, 5, 8, …}}9/5/2013