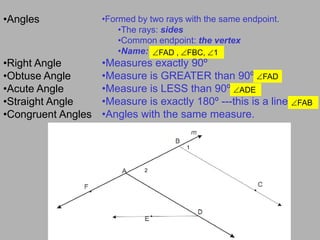
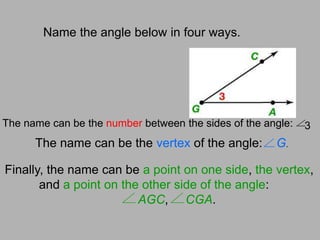
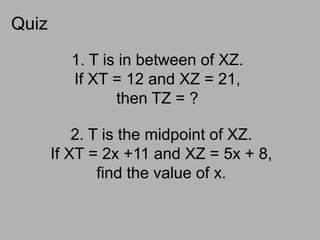The document outlines key concepts in geometry, focusing on measuring segments and angles, including formulas for calculating lengths and midpoints on a number line and coordinate plane. It also explains the angle addition postulate and provides examples and exercises to reinforce understanding. Lastly, it highlights classifications of angles and relationships between their measures.

1. 1.4: Measuring Segments and AnglesPrentice Hall Geometry

2. CEABD0-88-2-4-1246-6The numerical location of a point on a number line.Coordinate :On a number line length AB = AB = |B - A|Length :On a number line, midpoint of AB = 1/2 (B+A) Midpoint :

3. Find which two of the segments XY, ZY, and ZW are congruent. Because XY = ZW, XYZW.Measuring Segments and AnglesGEOMETRY LESSON 1-4Find the length of each segment.XY = | –5 – (–1)| = | –4| = 4ZY = | 2 – (–1)| = |3| = 3ZW = | 2 – 6| = |–4| = 4

4. The Segment Addition PostulateIf three points A, B, and C are collinear and B is between A and C, then AB + BC = AC.ABC

5. AN = 2x – 6 = 2(8) – 6 = 10NB = x + 7 = (8) + 7 = 15Substitute 8 for x.If AB = 25, find the value of x. Then find AN and NB.Use the Segment Addition Postulate to write an equation.AN + NB = ABSegment Addition Postulate(2x – 6) + (x + 7) = 25 Substitute.3x + 1 = 25 Simplify the left side. 3x = 24 Subtract 1 from each side.x = 8 Divide each side by 3.AN = 10 and NB = 15, which checks because the sum of the segment lengths equals 25.

6. RM = 5x + 9 = 5(15) + 9 = 84 MT = 8x – 36 = 8(15) – 36 = 84Substitute 15 for x.RM and MT are each 84, which is half of 168, the length of RT.Mis the midpoint of RT. Find RM, MT, and RT.Use the definition of midpoint to write an equation.RM = MTDefinition of midpoint5x + 9 = 8x – 36Substitute.5x + 45 = 8xAdd 36 to each side. 45 = 3xSubtract 5x from each side. 15 = xDivide each side by 3.RT = RM + MT= 168

7. Quiz1. T is in between of XZ. If XT = 12 and XZ = 21, then TZ = ?2. T is the midpoint of XZ. If XT = 2x +11 and XZ = 5x + 8, find the value of x.

8. Coordinate Plane

9. Parts of Coordinate Planey-axisQuadrant IIQuadrant I( - , + )( +, + )originx-axisQuadrant IIIQuadrant IV( - , - )( + , - )

10. DistanceOn a number line formula: d = | x2 – x1 |On a coordinate plane formula:

11. Find the distance between T(5, 2) and R( -4. -1) to the nearest tenth.

12. MidpointOn a number line formula: On a coordinate plane formula:

13. The midpoint of AB is M(3, 4). One endpoint is A(-3, -2). Find the coordinates of the other endpoint B.

14. Angles

15. Formed by two rays with the same endpoint.

16. The rays: sides

17. Common endpoint: the vertex

18. Name:

19. Measures exactly 90º