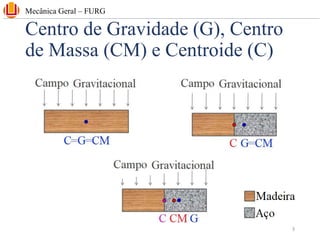
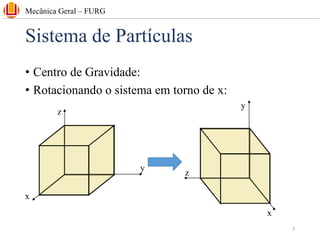
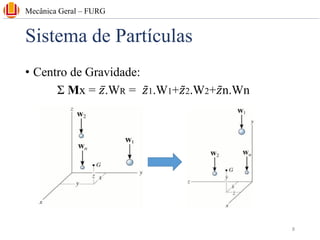
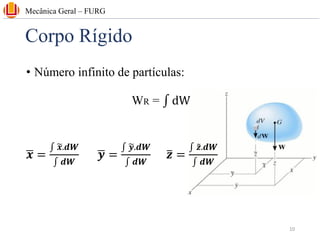
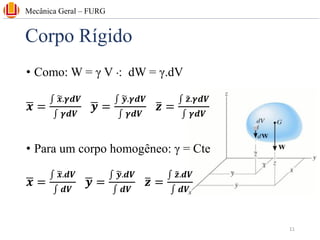
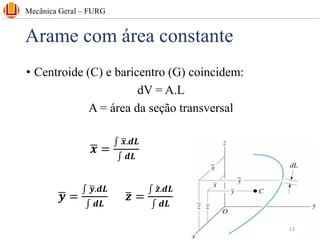
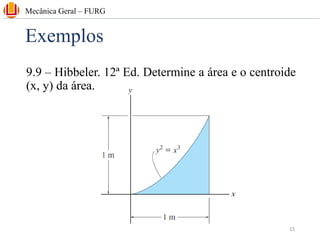
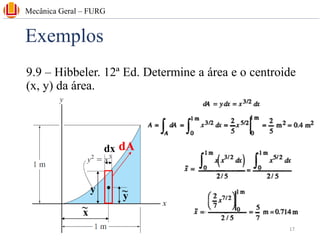
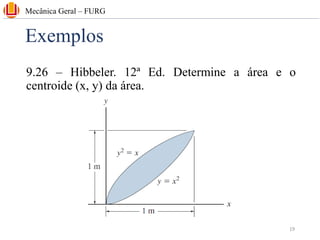
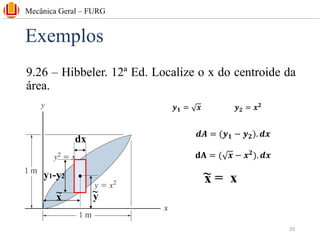
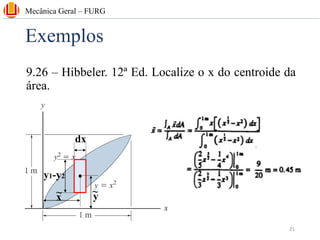
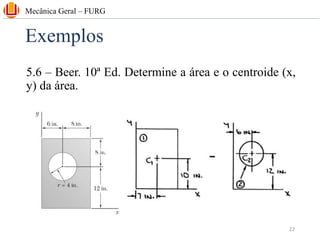
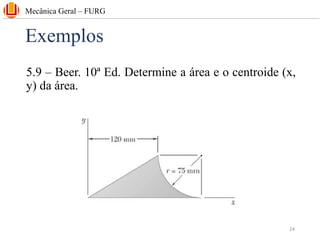
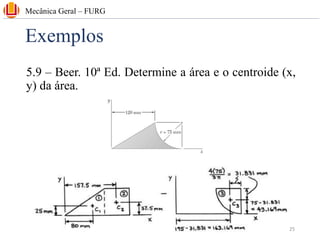
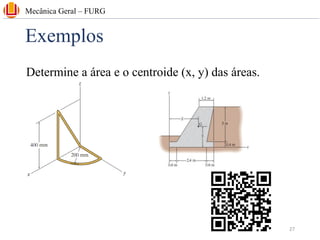
The document discusses concepts related to center of gravity (G), center of mass (CM), and centroid (C) for particle systems and rigid bodies. It provides definitions and formulas for calculating the x, y, and z coordinates of these points for different geometries, including planar homogeneous plates, wires with constant cross-sectional area, and composite bodies made of multiple parts. Examples are presented on calculating the area and centroid of various shapes using formulas from mechanics textbooks.

1. Centro de Gravidade,
Centro de Massa e
Centroide
Profª Fernanda Mazuco Clain
Universidade Federal do Rio Grande – FURG
Mecânica Geral

2. Cargas pontuais
• Cargas pontuais são abstrações de cargas
distribuídas em domínios com dimensões
características pequenas comparadas com as do
elemento estrutural ao qual estão aplicadas ou de
representação de um sistema resultante equivalente
de forças distribuídas.
Mecânica Geral – FURG
2

3. Centro de Gravidade (G), Centro
de Massa (CM) e Centroide (C)
Mecânica Geral – FURG
3

4. Sistema de Partículas
Mecânica Geral – FURG
4

5. Sistema de Partículas
• As partículas com pesos W1, ..., Wn podem ser
substituídas por uma força resultante WR localizada
no centro de gravidade (G):
• Força resultante:
Σ F = WR = Σ W
Mecânica Geral – FURG
5

6. Sistema de Partículas
• Centro de Gravidade:
Σ My = ҧ
𝑥.WR = ෤
𝑥1.W1+෤
𝑥2.W2+෤
𝑥n.Wn
Σ Mx = ത
𝑦.WR = ෤
𝑦1.W1+෤
𝑦2.W2+෤
𝑦n.Wn
Mecânica Geral – FURG
6

7. Sistema de Partículas
• Centro de Gravidade:
• Rotacionando o sistema em torno de x:
Mecânica Geral – FURG
z
x
y
z
x
y
7

8. Sistema de Partículas
• Centro de Gravidade:
Σ Mx = ҧ
𝑧.WR = ǁ
𝑧1.W1+ ǁ
𝑧2.W2+ ǁ
𝑧n.Wn
Mecânica Geral – FURG
8

9. Sistema de Partículas
• Centro de Gravidade:
WR = Σ W
ҧ
𝑥.WR = ෤
𝑥1.W1+෤
𝑥2.W2+෤
𝑥n.Wn
ത
𝑦.WR = ෤
𝑦1.W1+෤
𝑦2.W2+෤
𝑦n.Wn
ҧ
𝑧.WR = ǁ
𝑧1.W1+ ǁ
𝑧2.W2+ ǁ
𝑧n.Wn
ഥ
𝒙 =
𝜮෥
𝒙.𝑾
𝜮𝑾
ഥ
𝒚 =
𝜮෥
𝒚.𝑾
𝜮𝑾
ത
𝒛 =
𝜮෤
𝒛.𝑾
𝜮𝑾
Mecânica Geral – FURG
9

10. Corpo Rígido
• Número infinito de partículas:
WR = ‫׬‬ dW
ഥ
𝒙 =
‫׬‬ ෥
𝒙.𝒅𝑾
‫׬‬ 𝒅𝑾
ഥ
𝒚 =
‫׬‬ ෥
𝒚.𝒅𝑾
‫׬‬ 𝒅𝑾
ത
𝒛 =
‫׬‬ ෤
𝒛.𝒅𝑾
‫׬‬ 𝒅𝑾
Mecânica Geral – FURG
10

11. Corpo Rígido
• Como: W = γ V ⁖ dW = γ.dV
ഥ
𝒙 =
‫׬‬ ෥
𝒙.𝜸𝒅𝑽
‫׬‬ 𝜸𝒅𝑽
ഥ
𝒚 =
‫׬‬ ෥
𝒚.𝜸𝒅𝑽
‫׬‬ 𝜸𝒅𝑽
ത
𝒛 =
‫׬‬ ෤
𝒛.𝜸𝒅𝑽
‫׬‬ 𝜸𝒅𝑽
• Para um corpo homogêneo: γ = Cte
ഥ
𝒙 =
‫׬‬ ෥
𝒙.𝒅𝑽
‫׬‬ 𝒅𝑽
ഥ
𝒚 =
‫׬‬ ෥
𝒚.𝒅𝑽
‫׬‬ 𝒅𝑽
ത
𝒛 =
‫׬‬ ෤
𝒛.𝒅𝑽
‫׬‬ 𝒅𝑽
Mecânica Geral – FURG
11

12. Placa plana homogênea
• Centroide (C) e baricentro (G) coincidem:
dV = e .dA
e = espessura
ഥ
𝒙 =
‫׬‬ ෥
𝒙.𝒅𝑨
‫׬‬ 𝒅𝑨
ഥ
𝒚 =
‫׬‬ ෥
𝒚.𝒅𝑨
‫׬‬ 𝒅𝑨
ത
𝒛 =
‫׬‬ ෤
𝒛.𝒅𝑨
‫׬‬ 𝒅𝑨
Mecânica Geral – FURG
12

13. Arame com área constante
• Centroide (C) e baricentro (G) coincidem:
dV = A.L
A = área da seção transversal
ഥ
𝒙 =
‫׬‬ ෥
𝒙.𝒅𝑳
‫׬‬ 𝒅𝑳
ഥ
𝒚 =
‫׬‬ ෥
𝒚.𝒅𝑳
‫׬‬ 𝒅𝑳
ത
𝒛 =
‫׬‬ ෤
𝒛.𝒅𝑳
‫׬‬ 𝒅𝑳
Mecânica Geral – FURG
13

14. Corpos Compostos
• Um corpo pode ser dividido em corpos com
centroide e/ou baricentro conhecido
• Dessa forma, cada parte pode ser tratada como uma
partícula
ഥ
𝒙 =
𝜮෥
𝒙.𝑾
𝜮𝑾
ഥ
𝒚 =
𝜮෥
𝒚.𝑾
𝜮𝑾
ത
𝒛 =
𝜮෤
𝒛.𝑾
𝜮𝑾
Mecânica Geral – FURG
x
y
+
_
= 1 2 3
14

15. Exemplos
9.9 – Hibbeler. 12ª Ed. Determine a área e o centroide
(x, y) da área.
Mecânica Geral – FURG
15

16. Exemplos
9.9 – Hibbeler. 12ª Ed. Determine a área e o centroide
(x, y) da área.
Mecânica Geral – FURG
y
y
~
x
~
dx dA
y
~ = _y_
2
x
~ = x
dA= y.dx
16

17. Exemplos
9.9 – Hibbeler. 12ª Ed. Determine a área e o centroide
(x, y) da área.
Mecânica Geral – FURG
y
y
~
x
~
dx dA
17

18. Exemplos
9.9 – Hibbeler. 12ª Ed. Determine a área e o centroide
(x, y) da área.
Mecânica Geral – FURG
y
y
~
x
~
dx dA
18

19. Exemplos
9.26 – Hibbeler. 12ª Ed. Determine a área e o
centroide (x, y) da área.
Mecânica Geral – FURG
19

20. Exemplos
9.26 – Hibbeler. 12ª Ed. Localize o x do centroide da
área.
Mecânica Geral – FURG
y1-y2
x
~ y
~
dx
𝒚𝟏 = 𝒙 𝒚𝟐 = 𝒙𝟐
𝒅𝑨 = (𝒚𝟏 − 𝒚𝟐). 𝒅𝒙
𝐝𝐀 = ( 𝒙 − 𝒙𝟐). 𝒅𝒙
x
~ = x
20

21. Exemplos
9.26 – Hibbeler. 12ª Ed. Localize o x do centroide da
área.
Mecânica Geral – FURG
y1-y2
x
~ y
~
dx
21

22. Exemplos
5.6 – Beer. 10ª Ed. Determine a área e o centroide (x,
y) da área.
Mecânica Geral – FURG
22

23. Exemplos
5.6 – Beer. 10ª Ed. Determine a área e o centroide (x,
y) da área.
Mecânica Geral – FURG
23

24. Exemplos
5.9 – Beer. 10ª Ed. Determine a área e o centroide (x,
y) da área.
Mecânica Geral – FURG
24

25. Exemplos
5.9 – Beer. 10ª Ed. Determine a área e o centroide (x,
y) da área.
Mecânica Geral – FURG
25

26. Exemplos
5.9 – Beer. 10ª Ed. Determine a área e o centroide (x,
y) da área.
Mecânica Geral – FURG
26

27. Exemplos
Mecânica Geral – FURG
27
Determine a área e o centroide (x, y) das áreas.