Introduction to FDA and linear models

Introduction to FDA and linear models
Nathalie Villa-Vialaneix - nathalie.villa@math.univ-toulouse.fr
http://www.nathalievilla.org
Institut de Mathématiques de Toulouse - IUT de Carcassonne, Université de Perpignan
France
La Havane, September 15th, 2008
Nathalie Villa (IMT & UPVD) Presentation 1 La Havane, Sept. 15th, 2008 1 / 37

Table of contents
1 Motivations
2 Functional Principal Component Analysis
3 Functional linear regression models
4 References

What is Functional Data Analysis (FDA)?
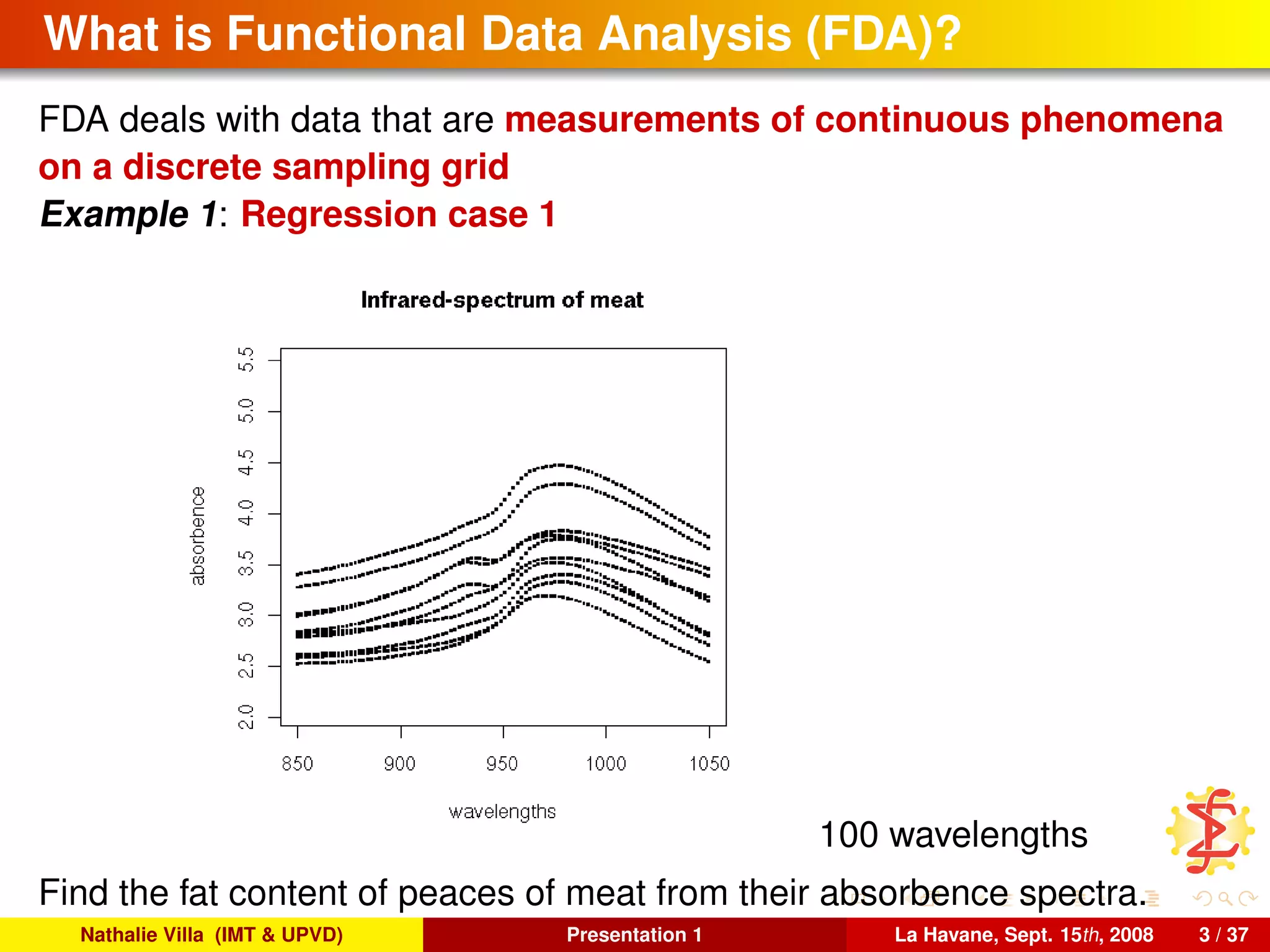
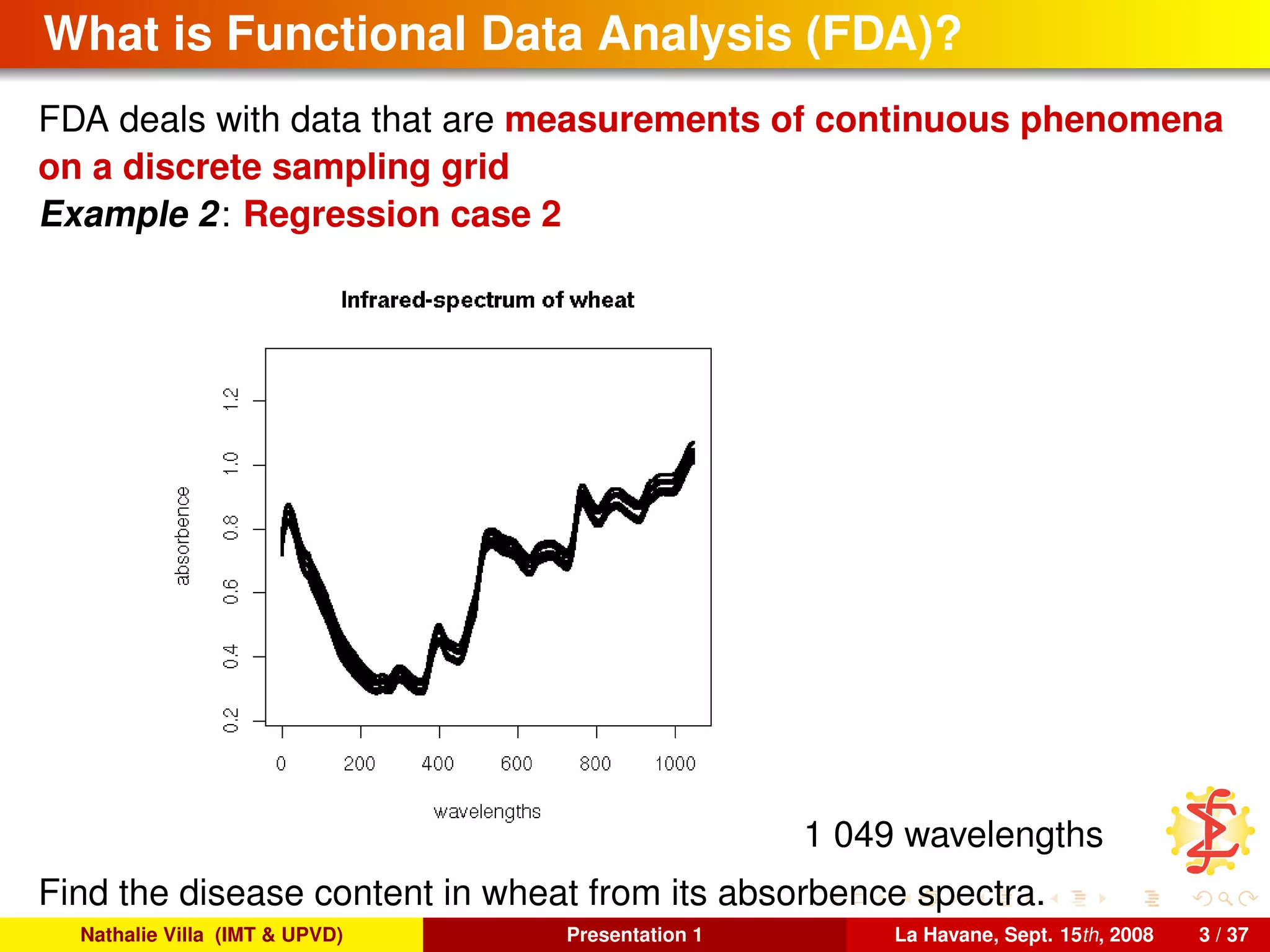
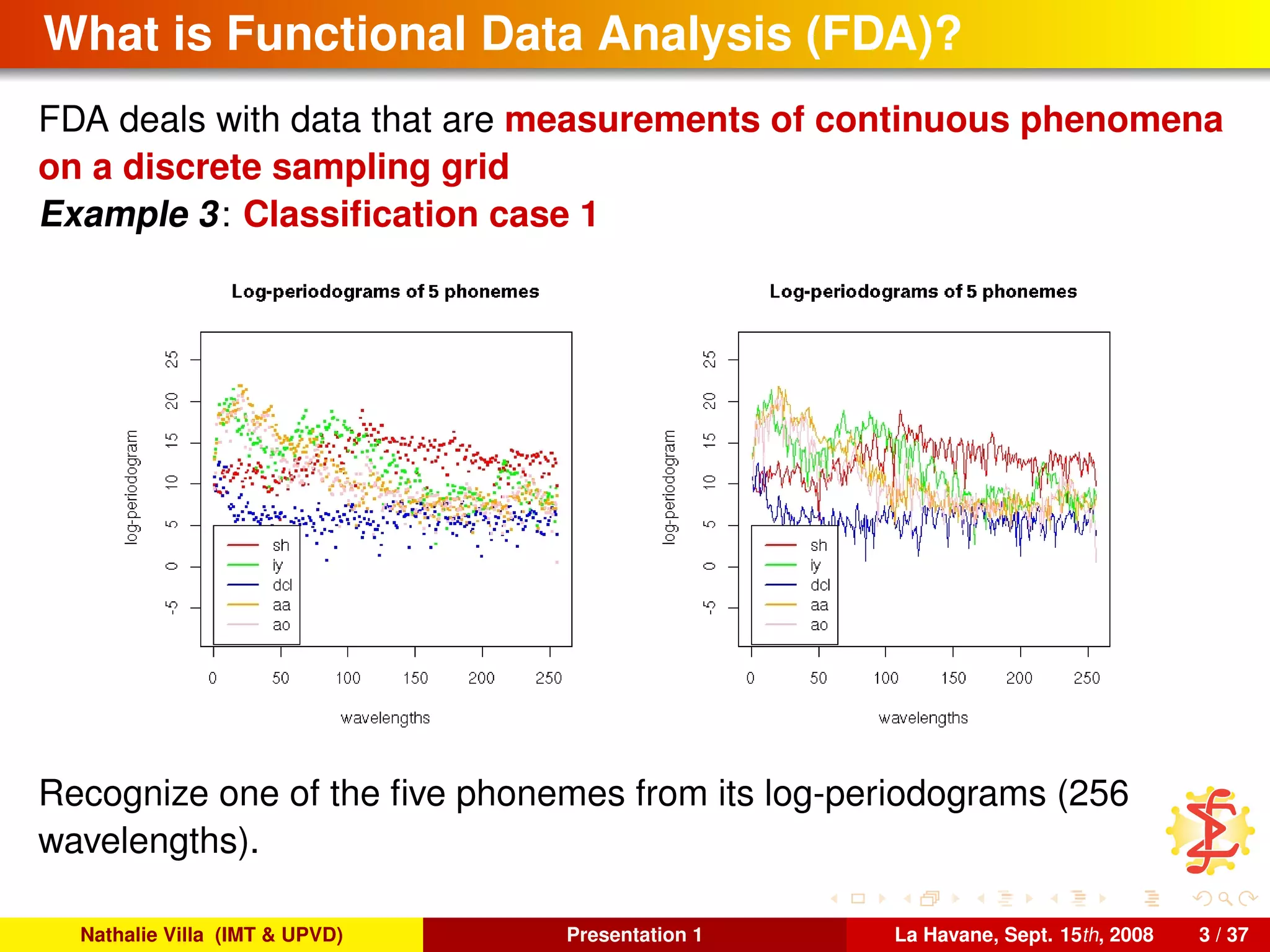
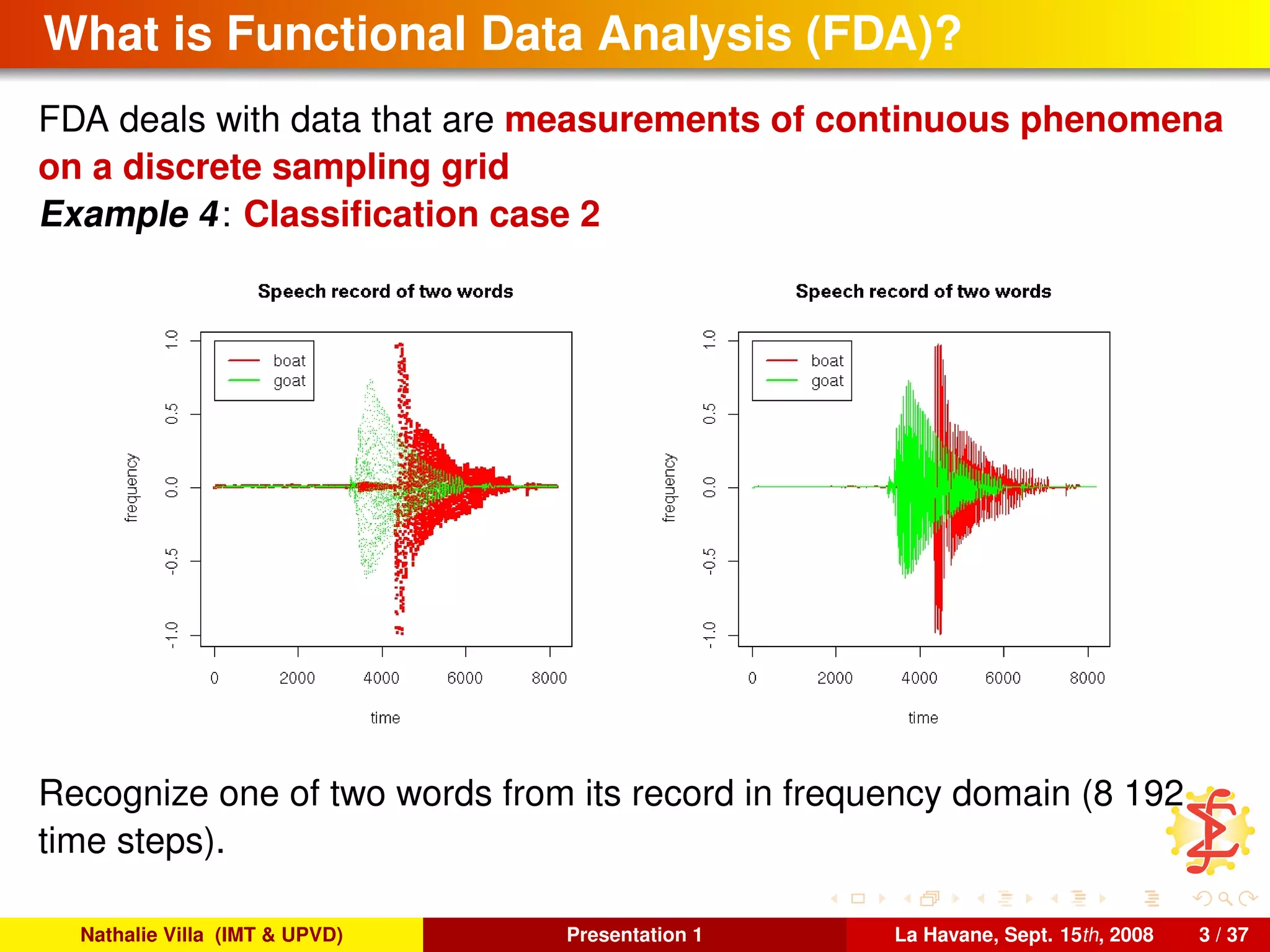
FDA deals with data that are measurements of continuous phenomena
on a discrete sampling grid

Example 1: Regression case 1
100 wavelengths
Find the fat content of peaces of meat from their absorbence spectra.

Example 2: Regression case 2
1 049 wavelengths
Find the disease content in wheat from its absorbence spectra.

Example 3: Classiﬁcation case 1
Recognize one of the ﬁve phonemes from its log-periodograms (256
wavelengths).

Example 4: Classiﬁcation case 2
Recognize one of two words from its record in frequency domain (8 192
time steps).

Example 5: Regression on functional data
[Azaïs et al., 2008]
Estimate a typical load curve (electricity consumption) from economic
multivariate variables.

Example 6: Curves clustering
[Bensmail et al., 2005]
Create a typology of sick cells from their “SELDI mass” spectra.

Speciﬁc issues of learning with FDA
High dimensional data (the number of discretization point is often
bigger or much more bigger than the number of observations);
Highly correlated data (because of the functional structure
underlined, the values at two sampling points are correlated).

Speciﬁc issues of learning with FDA
High dimensional data (the number of discretization point is often
bigger or much more bigger than the number of observations);
Highly correlated data (because of the functional structure
underlined, the values at two sampling points are correlated).
Consequences: Direct use of classical statistical methods on the
discretization leads to ill-posed problems and provides inaccurate
solutions.

Theoretical model
A functional random variable is a random variable X taking its values in
a functional space X where X can be:
a (inﬁnite dimensional) Hilbert space with inner product ., . X;

Theoretical model
in particular, L2
is often used;

Theoretical model
in particular, L2
is often used;
any (inﬁnite dimensional) Banach space with norm . X (less usual);
for example, C0
.

Hilbertian context
In the hilbertian context, we are able to deﬁne
the expectation of X as (Theorem of Riesz) the unique element
E (X) of X such that
∀ u ∈ X, E (X) , u X = E ( X, u X) ,
1

Hilbertian context
∀ u ∈ X, E (X) , u X = E ( X, u X) ,
for any u1, u2 ∈ X, u1 ⊗ u2 is the linear operator
u1 ⊗ u2 : v ∈ X → u1, v Xu2 ∈ X,
1

Hilbertian context
∀ u ∈ X, E (X) , u X = E ( X, u X) ,
u1 ⊗ u2 : v ∈ X → u1, v Xu2 ∈ X,
as (X − E (X)) ⊗ (X − E (X)) is an element of the Hilbert Space of
Hilbert-Schmidt operators from X to X, HS(X)1
1
This Hilbert space is equipped with the inner product
∀ g1, g2 ∈ HS(X), g1, g2 HS(X) = i g1ei, g2ei X where (ei)i is any orthonormal basis of X

Hilbertian context
∀ u ∈ X, E (X) , u X = E ( X, u X) ,
u1 ⊗ u2 : v ∈ X → u1, v Xu2 ∈ X,
as (X − E (X)) ⊗ (X − E (X)) is an element of the Hilbert Space of
Hilbert-Schmidt operators from X to X, HS(X)1
the variance of X
as the linear operator ΓX
ΓX = E ((X − E (X)) ⊗ (X − E (X))) : u ∈ X →
E ( X − E (X) , u X(X − E (X))) .
1
This Hilbert space is equipped with the inner product
∀ g1, g2 ∈ HS(X), g1, g2 HS(X) = i g1ei, g2ei X where (ei)i is any orthonormal basis of X

Case X = L2
([0, 1])
if X = L2
([0, 1]), this expressions simplify in:
norm: X 2
= [0,1]
(X(t))2
dt < +∞;

Case X = L2
([0, 1])
if X = L2
norm: X 2
= [0,1]
(X(t))2
dt < +∞;
expectation: for all t ∈ [0, 1],
E (X) (t) = E (X(t)) = X(t)dPX ,

Case X = L2
([0, 1])
if X = L2
norm: X 2
= [0,1]
(X(t))2
dt < +∞;
E (X) (t) = E (X(t)) = X(t)dPX ,
variance: for all t, t ∈ [0, 1],
ΓX γ(t, t ) = E (X(t)X(t ))
(if E (X) = 0 for clarity reasons)

Case X = L2
([0, 1])
if X = L2
norm: X 2
= [0,1]
(X(t))2
dt < +∞;
E (X) (t) = E (X(t)) = X(t)dPX ,
ΓX γ(t, t ) = E (X(t)X(t ))
(if E (X) = 0 for clarity reasons) because:
1 for all t ∈ [0, 1], we can deﬁne Γt
X
: u ∈ X → (ΓX u)(t) ∈ R,

Case X = L2
([0, 1])
if X = L2
norm: X 2
= [0,1]
(X(t))2
dt < +∞;
E (X) (t) = E (X(t)) = X(t)dPX ,
ΓX γ(t, t ) = E (X(t)X(t ))
X
: u ∈ X → (ΓX u)(t) ∈ R,
2 By Riesz’s Theorem, it exists ζt
∈ X such that ∀ u ∈ X, Γt
X
u = ζt
, u X.

Case X = L2
([0, 1])
if X = L2
norm: X 2
= [0,1]
(X(t))2
dt < +∞;
E (X) (t) = E (X(t)) = X(t)dPX ,
ΓX γ(t, t ) = E (X(t)X(t ))
X
: u ∈ X → (ΓX u)(t) ∈ R,
X
u = ζt
, u X.
As,
(ΓX u)(t) = E ( X, u XX(t))

Case X = L2
([0, 1])
if X = L2
norm: X 2
= [0,1]
(X(t))2
dt < +∞;
E (X) (t) = E (X(t)) = X(t)dPX ,
ΓX γ(t, t ) = E (X(t)X(t ))
X
: u ∈ X → (ΓX u)(t) ∈ R,
X
u = ζt
, u X.
As,
(ΓX u)(t) = E ( X(t)X, u X)

Case X = L2
([0, 1])
if X = L2
norm: X 2
= [0,1]
(X(t))2
dt < +∞;
E (X) (t) = E (X(t)) = X(t)dPX ,
ΓX γ(t, t ) = E (X(t)X(t ))
X
: u ∈ X → (ΓX u)(t) ∈ R,
X
u = ζt
, u X.
As,
(ΓX u)(t) = E (X(t)X), u X,

Case X = L2
([0, 1])
if X = L2
norm: X 2
= [0,1]
(X(t))2
dt < +∞;
E (X) (t) = E (X(t)) = X(t)dPX ,
ΓX γ(t, t ) = E (X(t)X(t ))
X
: u ∈ X → (ΓX u)(t) ∈ R,
X
u = ζt
, u X.
As,
(ΓX u)(t) = E (X(t)X), u X,
we have that ζt
= E (X(t)X) .

Case X = L2
([0, 1])
if X = L2
norm: X 2
= [0,1]
(X(t))2
dt < +∞;
E (X) (t) = E (X(t)) = X(t)dPX ,
ΓX γ(t, t ) = E (X(t)X(t ))
X
: u ∈ X → (ΓX u)(t) ∈ R,
X
u = ζt
, u X.
As,
(ΓX u)(t) = E (X(t)X), u X,
we have that ζt
= E (X(t)X) .
3 We deﬁne γ : (t, t ) ∈ [0, 1]2
→ ζt
(t ) = E (X(t)X(t ))

Properties of ΓX
ΓX is Hilbert-Schmidt:
(deﬁnition) i ΓX ei
2
< +∞;

Properties of ΓX
2
< +∞;
it exists a countable eigensystem of ΓX , ((λi)i≤1, (vi)i≥1): ΓX vi = λivi
(for all i ≤ 1).

Properties of ΓX
2
< +∞;
(for all i ≤ 1). This eigensystem is such that:
λ1 ≥ λ2 ≥ . . . ≥ 0 and 0 is the only possible accumulation value of (λi)i,

Properties of ΓX
2
< +∞;
Karhunen-Loeve decomposition of ΓX
ΓX =
i≥1
λivi ⊗ vi.

Properties of ΓX
2
< +∞;
ΓX =
i≥1
λivi ⊗ vi.
ΓX has no inverse in the space of continuous operator from X to X, if
X has inﬁnite dimension.

Properties of ΓX
2
< +∞;
ΓX =
i≥1
λivi ⊗ vi.
ΓX has no inverse in the space of continuous operator from X to X, if
X has inﬁnite dimension. More precisely, if λi > 0 for all i ≥ 1,
i≥1
1
λi
= +∞.

Model of the observed data
We focus on:
1 a regression problem: Y ∈ R has to be predicted from X ∈ X,
2 OR a (binary) classiﬁcation problem: Y ∈ {−1, 1} has to be
predicted from X ∈ X.

We focus on:
Learning set - Version 1
(x1, y1), . . . , (xn, yn) are i.i.d. realizations of the random pair (X, Y).

We focus on:
Learning set - Version 1
(x1, y1), . . . , (xn, yn) are i.i.d. realizations of the random pair (X, Y).
Remark: if E X 2
X < +∞ (i.e., if ΓX exists), a functional version of the
Central Limit Theorem exists.

Model of the uncertainty on X
In fact, realizations of X are never observed. Only a (possibly noisy)
discretization of them are given.

Learning set - Version II
(x1, y1), . . . , (xn, yn) are i.i.d. realizations of the random pair (X, Y) and for
all i = 1, . . . , n, xτi
i
= (xi(t))t∈τi is observed, where τi
is a ﬁnite set.

all i = 1, . . . , n, xτi
i
is a ﬁnite set.
Questions:
1 How to obtain (xi)i from (xτi
i
)i?

all i = 1, . . . , n, xτi
i
is a ﬁnite set.
Questions:
i
)i?
2 What are the consequences of this uncertainty on the accuracy of
the solution of the regression/classiﬁcation problem? Can we obtain a
solution that is as good as those obtained from the direct observation
of (xi)i?

Noisy data model
Learning set - Version III
all i = 1, . . . , n, xτi
i
= (xi(t) + it )t∈τi is observed, where τi
is a ﬁnite set
and it is a centered random variable independant of X.

Noisy data model
all i = 1, . . . , n, xτi
i
is a ﬁnite set
Again,
i
)i? (works have been done: function
estimation)

Noisy data model
all i = 1, . . . , n, xτi
i
is a ﬁnite set
Again,
i
estimation)
of (xi)i? (relating to “errors-in-variables” problems ; almost no work in
FDA)

Noisy data model
all i = 1, . . . , n, xτi
i
is a ﬁnite set
Again,
i
estimation)
of (xi)i? (relating to “errors-in-variables” problems ; almost no work in
FDA)
In these presentations, works coming from the three points of view.

Table of contents
1 Motivations
4 References

Multidimensional PCA: context and notations
Data:
A real matrix
X = (x
j
i
)i=1,...,n, j=1,...,p
which is the observation of p variables on n individuals.

Data:
A real matrix
X = (x
j
i
)i=1,...,n, j=1,...,p
n rows, each corresponding to the value of p variables for an
individual:
xi = (x1
i , . . . , x
p
i
)T
.

Data:
A real matrix
X = (x
j
i
)i=1,...,n, j=1,...,p
individual:
xi = (x1
i , . . . , x
p
i
)T
.
p columns, each corresponding to n observations of a variable:
xj
= (x
j
1
, . . . , x
j
n)T
.

Data:
A real matrix
X = (x
j
i
)i=1,...,n, j=1,...,p
individual:
xi = (x1
i , . . . , x
p
i
)T
.
p columns, each corresponding to n observations of a variable:
xj
= (x
j
1
, . . . , x
j
n)T
.
Aim: Find linearly independant variables, that are linear combinations of
the original ones, by order of “importance” in X.

First principal component
Suppose (to simplify)
1 Data are centered: for all j = 1, . . . , p, xj = 1
n
n
i=1 x
j
i
= 0;
2 The empirical variance of X is: for all j = 1, . . . , p, Var (X) = 1
n XT
X.

n
n
i=1 x
j
i
= 0;
n XT
X.
Problem: Find a∗ ∈ Rp
such that:
a∗
:= arg max
a: a Rp =1



Var Pa(xi) Rp
i
inertia



.

n
n
i=1 x
j
i
= 0;
n XT
X.
such that:
a∗
:= arg max
a: a Rp =1



Var Pa(xi) Rp
i
inertia



.
Solution:
Var Pa(xi) Rp
i
=
1
n
n
i=1
aT
xia
2
Rp

n
n
i=1 x
j
i
= 0;
n XT
X.
such that:
a∗
:= arg max
a: a Rp =1



Var Pa(xi) Rp
i
inertia



.
Solution:
Var Pa(xi) Rp
i
=
1
n
n
i=1
(aT
xi)2
a 2
Rp
=1

n
n
i=1 x
j
i
= 0;
n XT
X.
such that:
a∗
:= arg max
a: a Rp =1



Var Pa(xi) Rp
i
inertia



.
Solution:
Var Pa(xi) Rp
i
=
1
n
n
i=1
(aT
xi)(xT
i a)

n
n
i=1 x
j
i
= 0;
n XT
X.
such that:
a∗
:= arg max
a: a Rp =1



Var Pa(xi) Rp
i
inertia



.
Solution:
Var Pa(xi) Rp
i
= aT


1
n
n
i=1
xixT
i

 a

n
n
i=1 x
j
i
= 0;
n XT
X.
such that:
a∗
:= arg max
a: a Rp =1



Var Pa(xi) Rp
i
inertia



.
Solution:
Var Pa(xi) Rp
i
= aT
Var (X) a

n
n
i=1 x
j
i
= 0;
n XT
X.
such that:
a∗
:= arg max
a: a Rp =1



Var Pa(xi) Rp
i
inertia



.
Solution:
Var Pa(xi) Rp
i
= aT
Var (X) a
⇒ a∗ is the eigenvector of Var (X) associated with the biggest (positive)
eigenvalue.

An eigenvalue decomposition
Generalization
If ((λi)i=1,...,p, (ai)i=1,...,p) is the eigenvalue decomposition of Var (X) (by
decreasing order of the positive λi) then (ai) are the factorial axis of X.
The principal components of X are the coordinates of the projections of
the data onto these axis.

An eigenvalue decomposition
Generalization
If ((λi)i=1,...,p, (ai)i=1,...,p) is the eigenvalue decomposition of Var (X) (by
decreasing order of the positive λi) then (ai) are the factorial axis of X.
The principal components of X are the coordinates of the projections of
the data onto these axis.
Then, we have:
Var (X) =
p
j=1
λjajaT
j
and
xi =
p
j=1
(xT
i aj)
principal component c
j
i
aj.

Ordinary generalization of PCA in FDA
Data: x1, . . . , xn are n centered observations of a random functional
variable X taking its values in X.

Aim: Find a∗ ∈ X such that:
a∗
:= arg max
a: a X=1
Var Pa(xi) X i
.

a∗
:= arg max
a: a X=1
Var Pa(xi) X i
.
Solution:
Var Pa(xi) Rp
i
=
1
n
n
i=1
a, xi Xa 2
X

a∗
:= arg max
a: a X=1
Var Pa(xi) X i
.
Solution:
Var Pa(xi) Rp
i
=
1
n
n
i=1
a, xi
2
X a 2
X
=1

a∗
:= arg max
a: a X=1
Var Pa(xi) X i
.
Solution:
Var Pa(xi) Rp
i
=
1
n
n
i=1
a, a, xi Xxi X

a∗
:= arg max
a: a X=1
Var Pa(xi) X i
.
Solution:
Var Pa(xi) Rp
i
=
1
n
n
i=1
a, xi Xxi, a X

a∗
:= arg max
a: a X=1
Var Pa(xi) X i
.
Solution:
Var Pa(xi) Rp
i
= Γn
X a, a X
where Γn
X
= 1
n
n
i=1 xi ⊗ xi is the empirical estimate of ΓX and is of rank
almost equal to n (Hilbert-Schmidt operator).

a∗
:= arg max
a: a X=1
Var Pa(xi) X i
.
Solution:
Var Pa(xi) Rp
i
= Γn
X a, a X
where Γn
X
= 1
n
n
i=1 xi ⊗ xi is the empirical estimate of ΓX and is of rank
almost equal to n (Hilbert-Schmidt operator).
⇒ a∗ is the eigenvector of Γn
X
associated with the biggest (positive)
eigenvalue: Γn
X
a∗ = λ∗a∗.

Eigenvalue decomposition of Γn
X
Factorial axes and principal components
If ((λi)i≥1, (ai)i≥1) is the eigenvalue decomposition of Γn
X
(by decreasing
order of the positive λi) then (ai) are the factorial axis of x1, . . . , xn (note
that at most n λi are nonzero).

X
X
(by decreasing
The principal components of x1, . . . , xn are the coordinates of the
projections of the data onto these axis.

X
X
(by decreasing
The principal components of x1, . . . , xn are the coordinates of the
projections of the data onto these axis.
Then, we have:
Γn
X =
n
j=1
λjaj ⊗ aj
and
xi =
n
j=1
xi, aj X
principal component c
j
i
aj.

Example on Tecator dataset
Data:

Two ﬁrst factorial axes

3rd and 4th factorial axes

Link with the regression problem

Smoothness of the factorial axes
On a practical point of view, functional PCA in its original version is
computing as the multivariate PCA (on the discretization or on the
decomposition of the curves on a Hilbert basis).

Smoothness of the factorial axes
On a practical point of view, functional PCA in its original version is
computing as the multivariate PCA (on the discretization or on the
decomposition of the curves on a Hilbert basis).
Hence, if the original data is irregular, the factorial axes won’t be smooth:

Smooth functional PCA
Aims: Introduce a penalty in the optimization problem so as to obtain
smooth (regular) factorial axes.

Ordinary functional PCA:
a∗
:= arg max
a: a X=1
Var Pa(xi) X i
and hence a∗ is the eigenvector of Γn
X
associated with the biggest
eigenvalue.

Penalized functional PCA: if D2m
X ∈ X = L2
a∗
:= arg max
a: a X=1
Var Pa(xi) X i
+µ Dm
a
2
X
(µ > 0) and hence a∗ is the eigenvector of Γn
X
+ µD2m
associated with the
biggest eigenvalue.

Practical implementation of smooth PCA
Let (ek )k≥1 be any functional basis. Then,
1 Approximate the observations by xi = K
k=1 ξi
k
ek .

k=1 ξi
k
ek .
2 Approximate the derivatives of the (ek )k by D2m
ek = K
k=1 βk
k
ek .

k=1 ξi
k
ek .
ek = K
k=1 βk
k
ek .
3 Then, we can demonstrate that:
Γn
X a + µD2m
a =
K
k=1
1
n
n
i=1
((ξi
)T
Ea)ξi
k ek + µ(βT
k a)ek ,
where E is the matrix containing ( ek , ek X)k,k =1,...,K .

k=1 ξi
k
ek .
ek = K
k=1 βk
k
ek .
3 which implicates
Γn
X + µD2m
: a ∈ RK
→
K
k=1
1
n
n
i=1
((ξi
)T
Ea)ξi
+ µ(βT
a).

k=1 ξi
k
ek .
ek = K
k=1 βk
k
ek .
3 which implicates
Γn
X + µD2m
: a ∈ RK
→
K
k=1
1
n
n
i=1
((ξi
)T
Ea)ξi
+ µ(βT
a).
4 Smooth PCA is performed by an eigendecomposition of
1
n
n
i=1 ξi
(ξi
)T
E + µβT
.

k=1 ξi
k
ek .
ek = K
k=1 βk
k
ek .
3 which implicates
Γn
X + µD2m
: a ∈ RK
→
K
k=1
1
n
n
i=1
((ξi
)T
Ea)ξi
+ µ(βT
a).
4 Smooth PCA is performed by an eigendecomposition of
1
n
n
i=1 ξi
(ξi
)T
E + µβT
.
Remark: The decomposition D2m
ek = K
k=1 βk
k
ek is easy to obtain
when using a spline basis ⇒ splines are well designed to represent data
with smooth properties (see Presentation 4 for futher details).

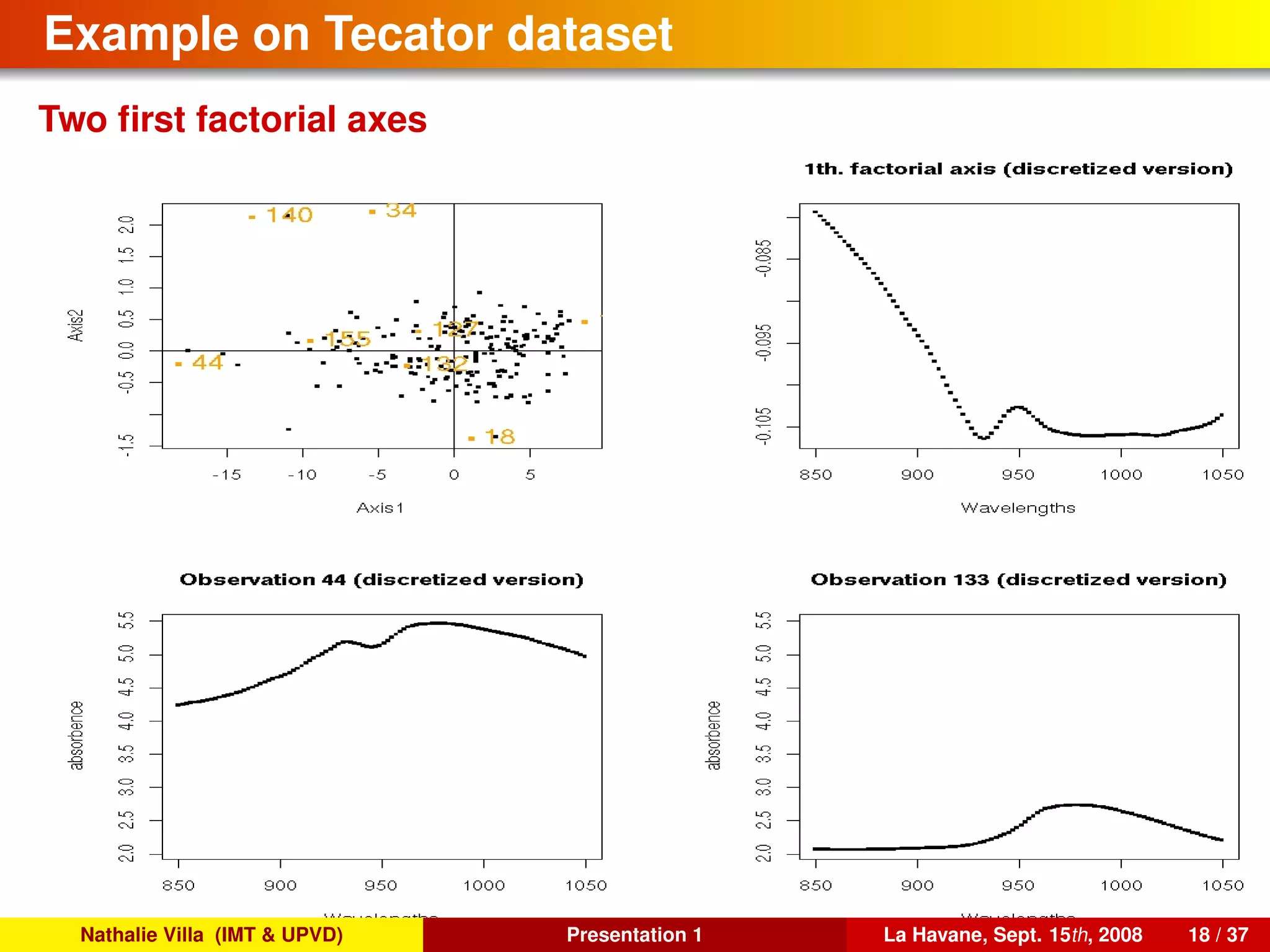
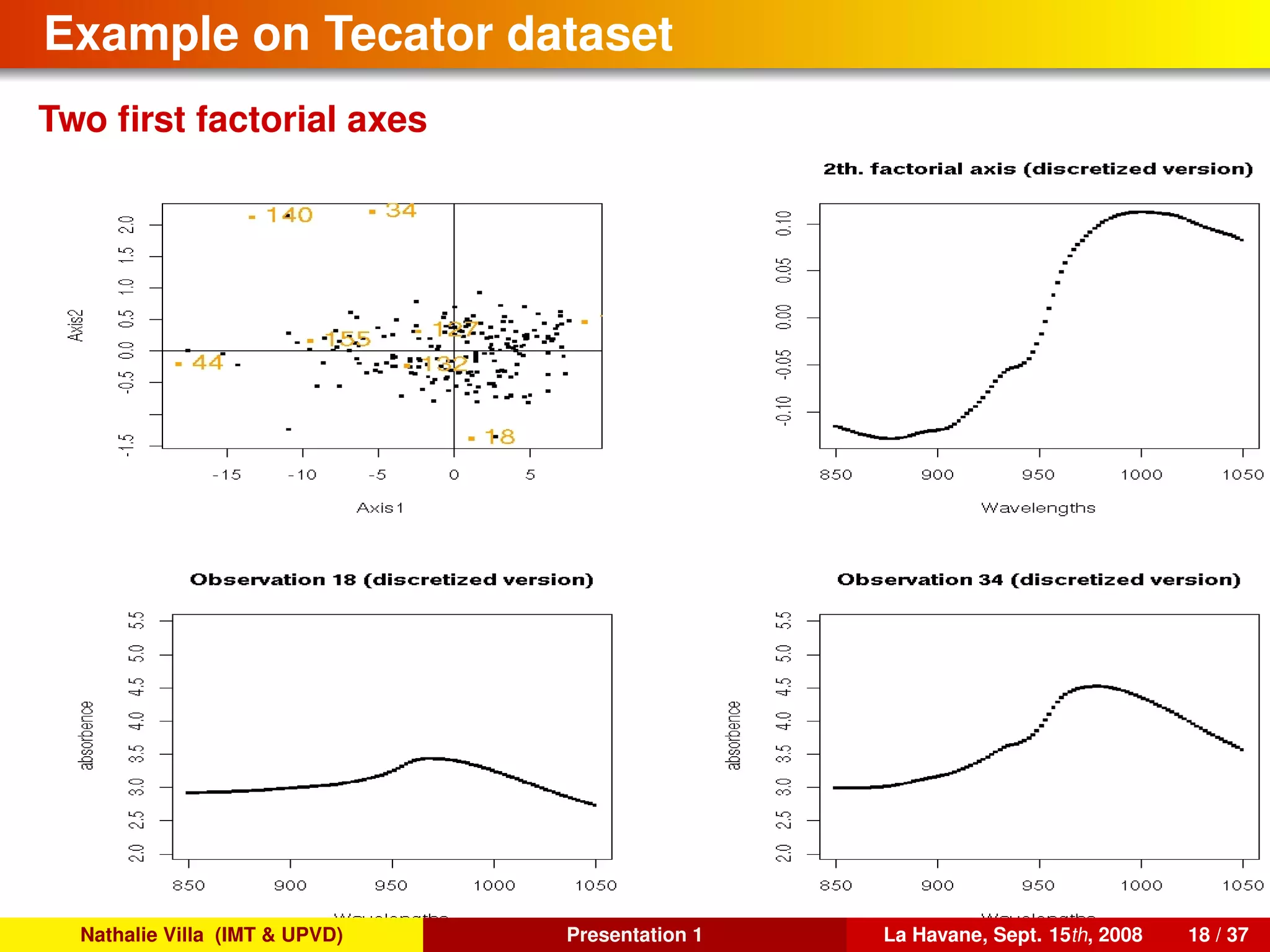
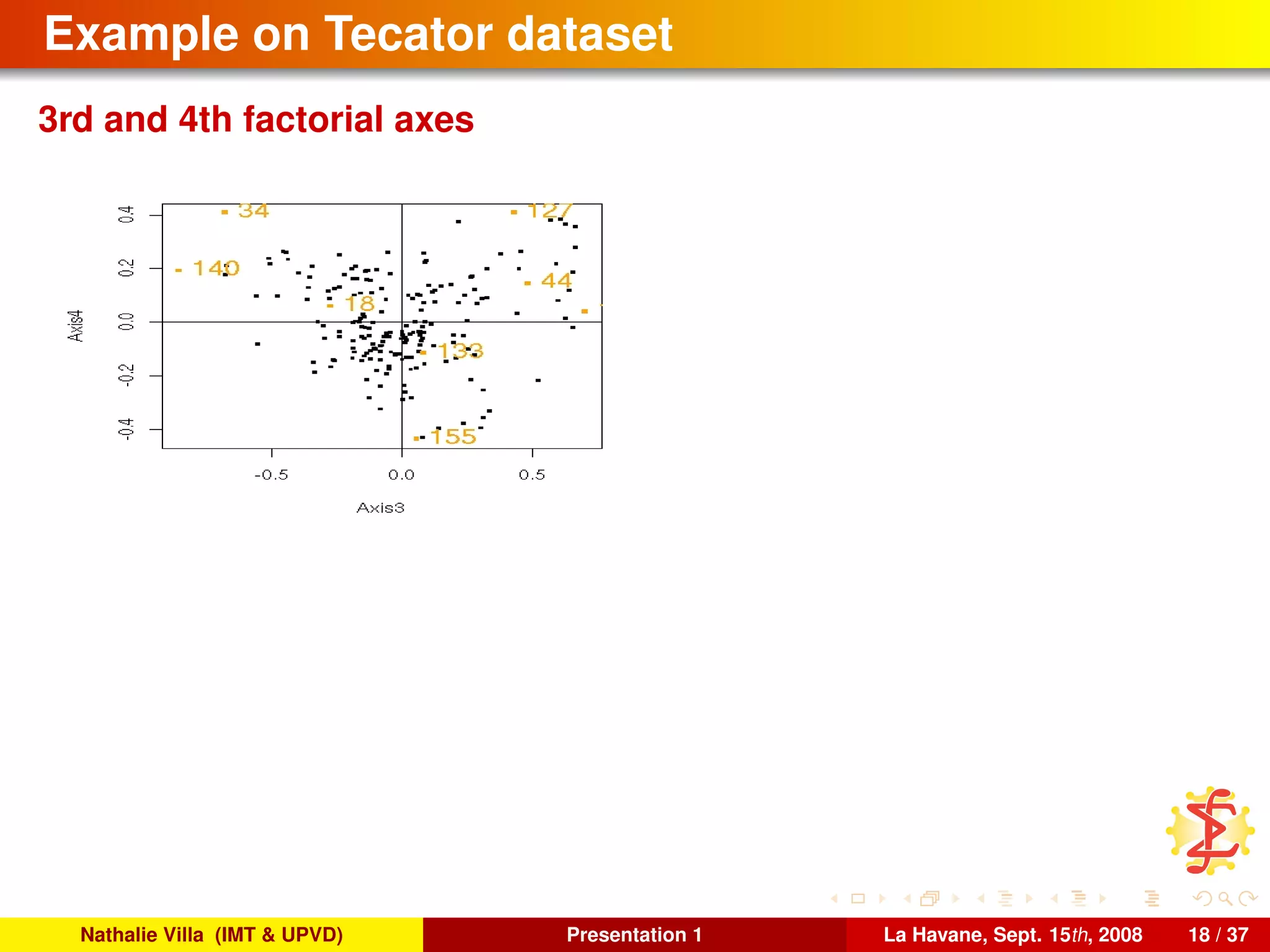
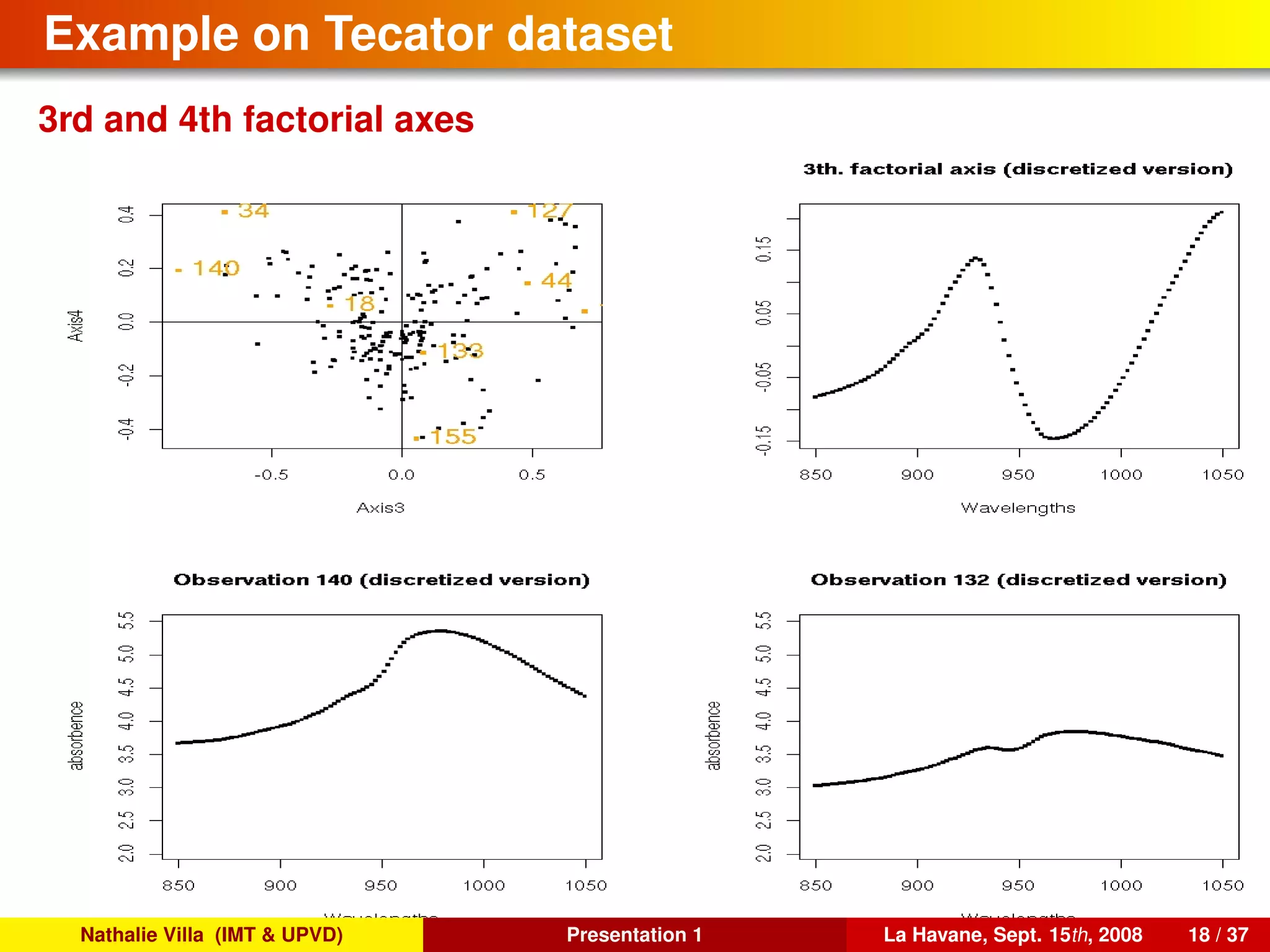
To conclude, several references. . .
Theoretical background for functional PCA:
[Deville, 1974]
[Dauxois and Pousse, 1976]
Smooth PCA:
[Besse and Ramsay, 1986]
[Pezzulli and Silverman, 1993]
[Silverman, 1996]
Several examples and discussion:
[Ramsay and Silverman, 2002]
[Ramsay and Silverman, 1997]

Table of contents
1 Motivations
4 References

The model
We are interested here in the functional linear regression model:
Y is a random variable taking its values in R,
X is a random variable taking its values in X,
X and Y satisfy the following model:
Y = X, α X +
where is a real random variable centered and independant of X and
α is the parameter to be estimated.

The model
Y = X, α X +
We are given a training set of size n, (xi, yi)i=1,...,n of independant
realizations of the random pair (X, Y).

The model
Y = X, α X +
Or, alternatively, we are given a training set of size n with
errors-in-variables: (wi, yi)i=1,...,n with:
wi = xi + ηi (ηi is the realization of a centered random variable
independant of Y)
yi = xi, α X + i
This problem will be investigated in Presentation 4

Basics about the functional linear regression model
To avoid useless difficulties, we will then suppose that E (X) = 0.
Let us first define the covariance between X and Y as:
∆(X,Y) = E (XY) ∈ X.

∆(X,Y) = E (XY) ∈ X.
Then, we have:
ΓX α = ∆(X,Y).

∆(X,Y) = E (XY) ∈ X.
Then, we have:
ΓX α = ∆(X,Y).
But, as ΓX is Hilbert-Schmidt, it is not invertible and thus, the empirical
estimate of α (using a generalized inverse of Γn
X
) does not converge to α
when n tends to inﬁnity. It is a ill-posed inverse problem.

∆(X,Y) = E (XY) ∈ X.
Then, we have:
ΓX α = ∆(X,Y).
But, as ΓX is Hilbert-Schmidt, it is not invertible and thus, the empirical
estimate of α (using a generalized inverse of Γn
X
) does not converge to α
when n tends to inﬁnity. It is a ill-posed inverse problem.
⇒ Penalization or regularization are needed to access a relevant
estimate.

PCA approach
References: [Cardot et al., 1999] from the works of [Bosq, 1991] on
hilbertian AR models.

PCA approach
PCA decomposition of X: Note
((λn
i
, vn
i
))i≥1 the eigenvalue decomposition of Γn
X
((λi)i are ordered in
decreasing order and almost n eigenvalues are not null; (vn
i
)i are
orthonormal)

PCA approach
((λn
i
, vn
i
X
i
)i are
orthonormal)
kn an integer such that: kn ≤ n and limn→+∞ kn = +∞

PCA approach
((λn
i
, vn
i
X
i
)i are
orthonormal)
Pkn the projector Pkn (u) = kn
i=1
vn
i
, . Xvn
i

PCA approach
((λn
i
, vn
i
X
i
)i are
orthonormal)
i=1
vn
i
, . Xvn
i
Γn,kn
X
= Pkn ◦ Γn,kn
X
◦ Pkn = 1
n
kn
i=1
λn
i
vn
i
, . Xvn
i

PCA approach
((λn
i
, vn
i
X
i
)i are
orthonormal)
i=1
vn
i
, . Xvn
i
Γn,kn
X
= Pkn ◦ Γn,kn
X
◦ Pkn = 1
n
kn
i=1
λn
i
vn
i
, . Xvn
i
∆n,kn
(X,Y)
= Pkn ◦ 1
n
n
i=1 yixi = 1
n i=1,...,n, i =1,...,kn
yi xi, vn
i Xvn
i

Deﬁnition of a consistent estimate for α
Deﬁne:
αn
= Γn,kn
X
+
∆n,kn
(X,Y)
where Γn,kn
X
+
denotes the generalized inverse (Moore-Penrose):
Γn,kn
X
+
=
kn
i=1
(λn
i )−1
vn
i , . Xvn
i .

Assumptions for consistency result
(A1) (λn
i
)i=1,...,kn are all distinct and not null a.s.
(A2) (λi)i≥1 are all distinct and not null
(A3) X is a.s. bounded in X ( X X ≤ C1 a.s.)
(A4) is a.s. bounded ( ≤ C2 a.s.)
(A5) limn→+∞
nλ4
kn
log n = +∞
(A6) limn→+∞
nλ2
kn
kn
j=1
aj
2
log n
= +∞ where a1 = 2
√
2
λ1−λ2
and
aj = 2
√
2
min(λj−1−λj;λj−λj+1)
for j > 1

(A1) (λn
i
)i=1,...,kn are all distinct and not null a.s.
(A2) (λi)i≥1 are all distinct and not null
(A3) X is a.s. bounded in X ( X X ≤ C1 a.s.)
(A4) is a.s. bounded ( ≤ C2 a.s.)
(A5) limn→+∞
nλ4
kn
log n = +∞
(A6) limn→+∞
nλ2
kn
kn
j=1
aj
2
log n
= +∞ where a1 = 2
√
2
λ1−λ2
and
aj = 2
√
2
min(λj−1−λj;λj−λj+1)
for j > 1
Example of ΓX satisfying those assumptions: if the eigenvalues of ΓX
are geometrically or exponentially decreasing, these assumptions are
fullﬁlled as long as the sequence (kn)n tends slowly enough to +∞.
For example, X is a Brownian motion on [0, 1] and kn = o(log n).

Consistency result
Theorem [Cardot et al., 1999]
Under assumptions (A1)-(A6), we have:
αn
− α X
n→+∞
−−−−−−→ 0

Smoothing approach based on B-splines
References: [Cardot et al., 2003]

Suppose that X takes values in L2
([0, 1]).
Basics on B-splines: Let q and k be to integers and denotes by Sqk the
space of functions satisfying:
s ∈ Sqk are polynomials of degree q on each interval l−1
k , l
k for all
l = 1, . . . , k,
s ∈ Sqk are q − 1 times differentiable on [0, 1].

([0, 1]).
k , l
k for all
l = 1, . . . , k,
The space Sqk has dimension q + k and a normalized basis of Sqk is
denoted by {B
qk
j
, j = 1, . . . , q + k} (normalized B-Splines, see
[de Boor, 1978]).

([0, 1]).
k , l
k for all
l = 1, . . . , k,
The space Sqk has dimension q + k and a normalized basis of Sqk is
denoted by {B
qk
j
, j = 1, . . . , q + k} (normalized B-Splines, see
[de Boor, 1978]).
These functions are easy to manipulate and have interesting smoothness
properties. They can be used to express either X and the parameter α as
well as to impose smoothness constrains on α.

Note Bqk := B
qk
1
, . . . , B
qk
q+k
T
and B
(m)
qk
the m derivatives of Bqk for a
m < q + k.

Note Bqk := B
qk
1
, . . . , B
qk
q+k
T
and B
(m)
qk
m < q + k.
A penalized mean square estimate: Providing the fact that αn
is smooth
enough, we aim at ﬁnding αn
= q+k
j=1
an
j
B
qk
j
= (an
)T
Bqk solution of the
optimization problem:
arg min
a∈Rq+k
1
n
n
i=1
yi − aT
Bqk , xi X
2
+ µ aT
B
(m)
qk
2
X

Note Bqk := B
qk
1
, . . . , B
qk
q+k
T
and B
(m)
qk
m < q + k.
is smooth
= q+k
j=1
an
j
B
qk
j
= (an
)T
Bqk solution of the
arg min
a∈Rq+k
1
n
n
i=1
yi − aT
Bqk , xi X
2
mean square criterion
+µ aT
B
(m)
qk
2
X
smoothness penalization

Note Bqk := B
qk
1
, . . . , B
qk
q+k
T
and B
(m)
qk
m < q + k.
is smooth
= q+k
j=1
an
j
B
qk
j
= (an
)T
Bqk solution of the
arg min
a∈Rq+k
1
n
n
i=1
yi − aT
Bqk , xi X
2
mean square criterion
+µ aT
B
(m)
qk
2
X
smoothness penalization
The solution of the previous problem is given by
an
= Cn
+ µGn
qk
−1
bn
where Cn
is the matrix with components Γn
X
B
qk
j
, B
qk
j X
(j, j = 1, . . . , q + k), bn
is the vector with components ∆n
(X,Y)
, B
qk
j X
(j = 1, . . . , q + k) and Gn
qk
is the matrix with components B
qk(m)
j
, B
qk(m)
j X
(j, j = 1, . . . , q + k).

(A1) X is a.s. bounded in X
(A2) Var (Y|X = x) ≤ C1 for all x ∈ X
(A3) E (Y|X = x) ≤ C2 for all x ∈ X
(A4) it exists an integer p and a real ν ∈ [0, 1] such that p + ν ≤ q
and α(p )(t1) − α(p )(t2) ≤ |t1 − t2|ν
(A5) µ = O n−(1−δ)/2
for a 0 < δ < 1
(A6) limn→+∞ µk2(m−p) = 0 for p = p + ν
(A7) k = O n1/(4p+1)

Consistency result
Theorem [Cardot et al., 2003]
Under assumptions (A1)-(A7),
limn→+∞ P (it exists a unique solution to the minimization problem) = 1
E αn
− α 2
X |x1, . . . , xn = OP n−2p/(4p+1)

Other functional linear methods
Canonical correlation: [Leurgans et al., 1993]
Factorial Discriminant Analysis: [Hastie et al., 1995]
Partial Least Squares: [Preda and Saporta, 2005]
. . .

Table of contents
1 Motivations
4 References

References
Further details for the references are given in the joint document.

Introduction to FDA and linear models

More Related Content

What's hot

Viewers also liked

Similar to Introduction to FDA and linear models

More from tuxette

Recently uploaded

Introduction to FDA and linear models