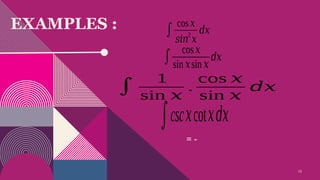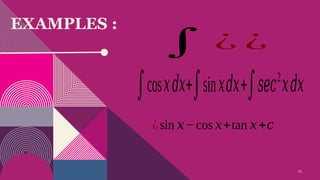Recommended
PDF
Phases of the Moon.pdf Physical science Education
PPTX
Finite square well in modern physics education.pptx
PDF
PRESENTATION-OF-SYNTHESIZED-Lesson-Plans-TTL-2.pdf
PPTX
Astronomy outline in Physical Science Education
PPTX
Introduction to Astronomy Presentation IN physical Science
PDF
493528170-Dale-s-Cone-of-Experiment 2.pdf
DOCX
viscosity report and outline for fluid mechanics
PDF
Report Meteorology earth annual energy balance
PDF
2024 Trend Updates: What Really Works In SEO & Content Marketing
PDF
Storytelling For The Web: Integrate Storytelling in your Design Process
PDF
Artificial Intelligence, Data and Competition – SCHREPEL – June 2024 OECD dis...
PDF
How to Leverage AI to Boost Employee Wellness - Lydia Di Francesco - SocialHR...
PDF
2024 State of Marketing Report – by Hubspot
PDF
Everything You Need To Know About ChatGPT
PDF
Product Design Trends in 2024 | Teenage Engineerings
PDF
How Race, Age and Gender Shape Attitudes Towards Mental Health
PDF
AI Trends in Creative Operations 2024 by Artwork Flow.pdf
PDF
PDF
PEPSICO Presentation to CAGNY Conference Feb 2024
PDF
Content Methodology: A Best Practices Report (Webinar)
PPTX
How to Prepare For a Successful Job Search for 2024
PDF
Social Media Marketing Trends 2024 // The Global Indie Insights
PDF
Trends In Paid Search: Navigating The Digital Landscape In 2024
PDF
5 Public speaking tips from TED - Visualized summary
PDF
ChatGPT and the Future of Work - Clark Boyd
PDF
Getting into the tech field. what next
PDF
Google's Just Not That Into You: Understanding Core Updates & Search Intent
PDF
How to have difficult conversations
More Related Content
PDF
Phases of the Moon.pdf Physical science Education
PPTX
Finite square well in modern physics education.pptx
PDF
PRESENTATION-OF-SYNTHESIZED-Lesson-Plans-TTL-2.pdf
PPTX
Astronomy outline in Physical Science Education
PPTX
Introduction to Astronomy Presentation IN physical Science
PDF
493528170-Dale-s-Cone-of-Experiment 2.pdf
DOCX
viscosity report and outline for fluid mechanics
PDF
Report Meteorology earth annual energy balance
Featured
PDF
2024 Trend Updates: What Really Works In SEO & Content Marketing
PDF
Storytelling For The Web: Integrate Storytelling in your Design Process
PDF
Artificial Intelligence, Data and Competition – SCHREPEL – June 2024 OECD dis...
PDF
How to Leverage AI to Boost Employee Wellness - Lydia Di Francesco - SocialHR...
PDF
2024 State of Marketing Report – by Hubspot
PDF
Everything You Need To Know About ChatGPT
PDF
Product Design Trends in 2024 | Teenage Engineerings
PDF
How Race, Age and Gender Shape Attitudes Towards Mental Health
PDF
AI Trends in Creative Operations 2024 by Artwork Flow.pdf
PDF
PDF
PEPSICO Presentation to CAGNY Conference Feb 2024
PDF
Content Methodology: A Best Practices Report (Webinar)
PPTX
How to Prepare For a Successful Job Search for 2024
PDF
Social Media Marketing Trends 2024 // The Global Indie Insights
PDF
Trends In Paid Search: Navigating The Digital Landscape In 2024
PDF
5 Public speaking tips from TED - Visualized summary
PDF
ChatGPT and the Future of Work - Clark Boyd
PDF
Getting into the tech field. what next
PDF
Google's Just Not That Into You: Understanding Core Updates & Search Intent
PDF
How to have difficult conversations
Calculus in trigonometric integrals report 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16.