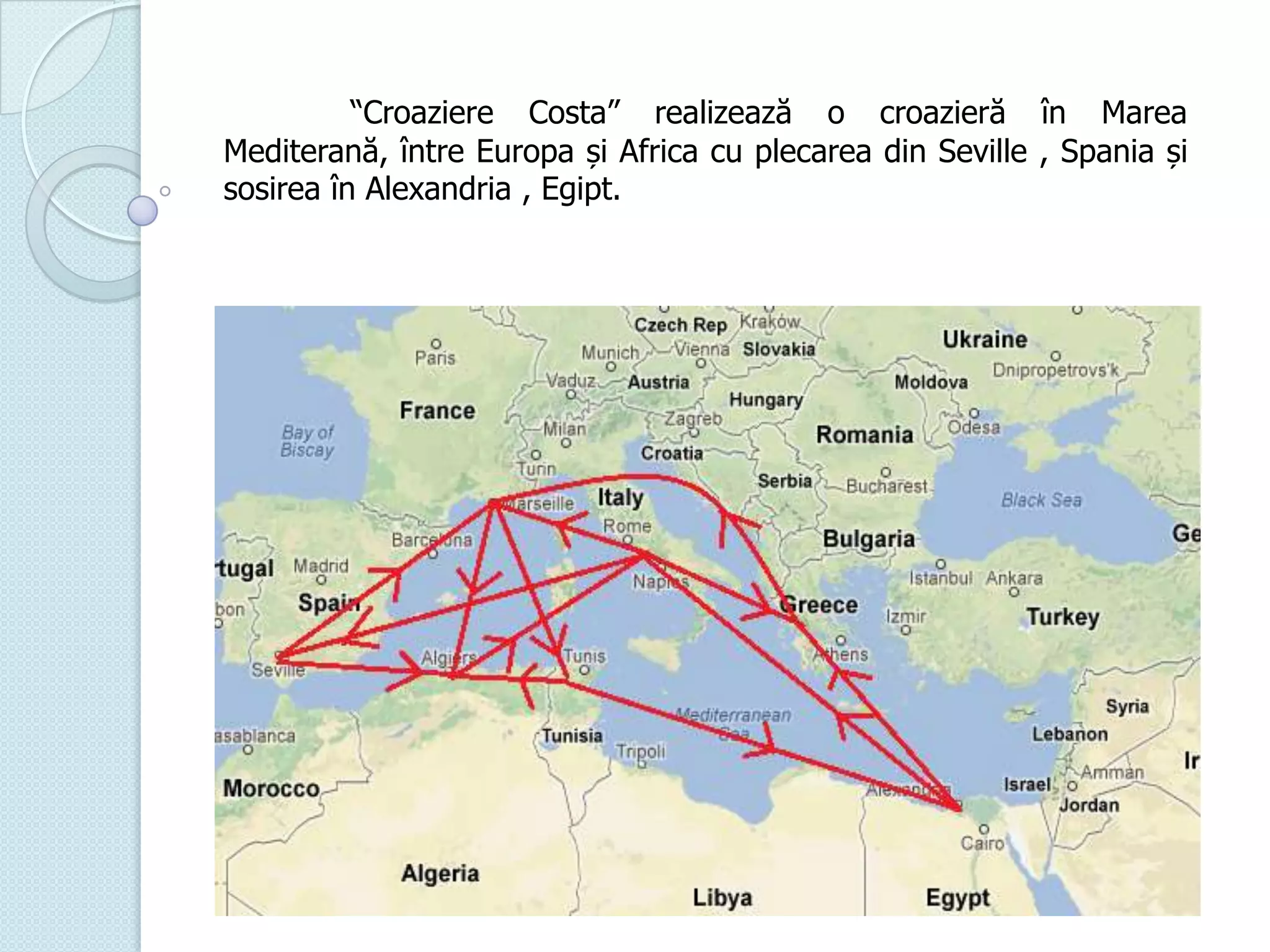
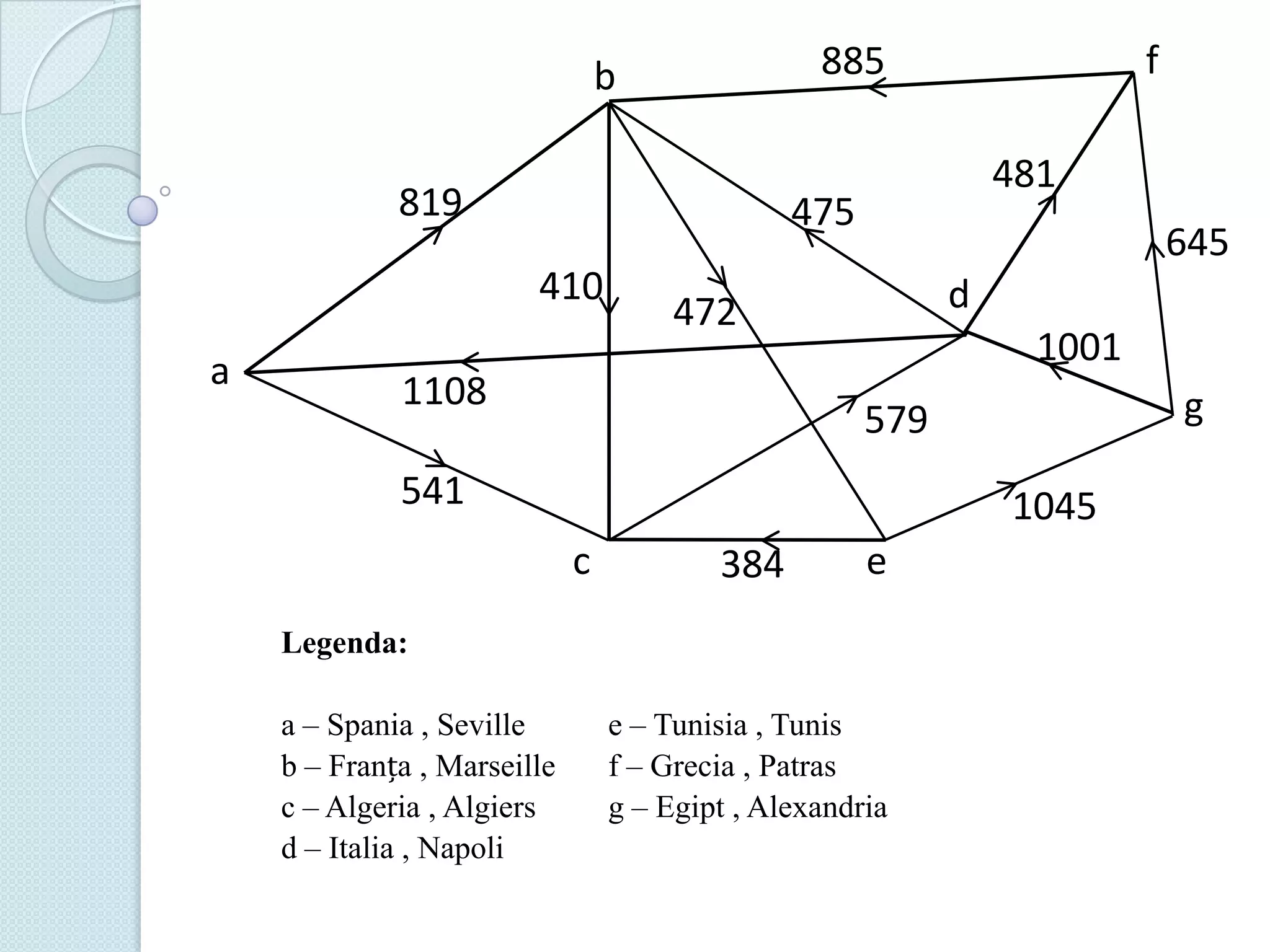
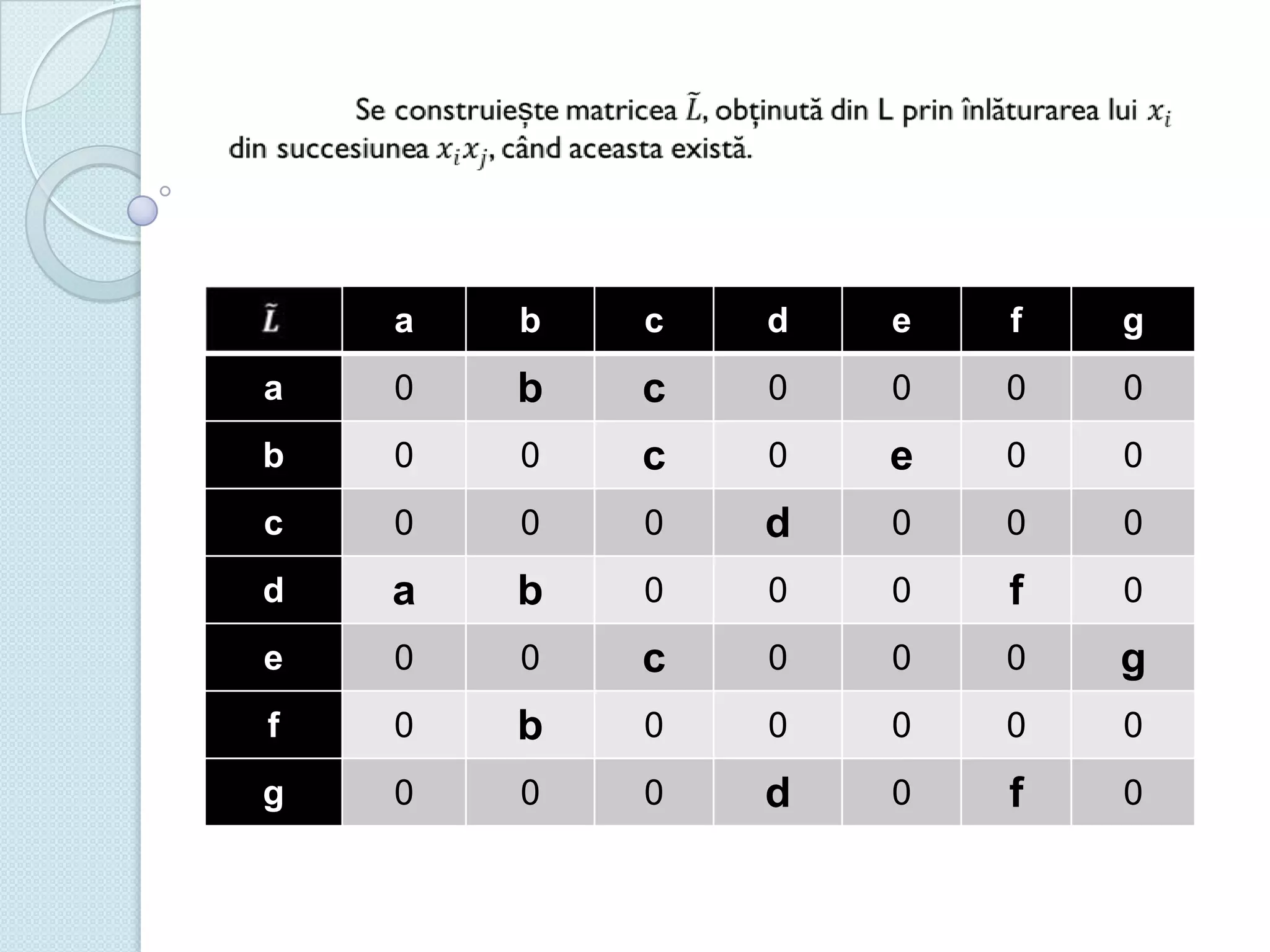
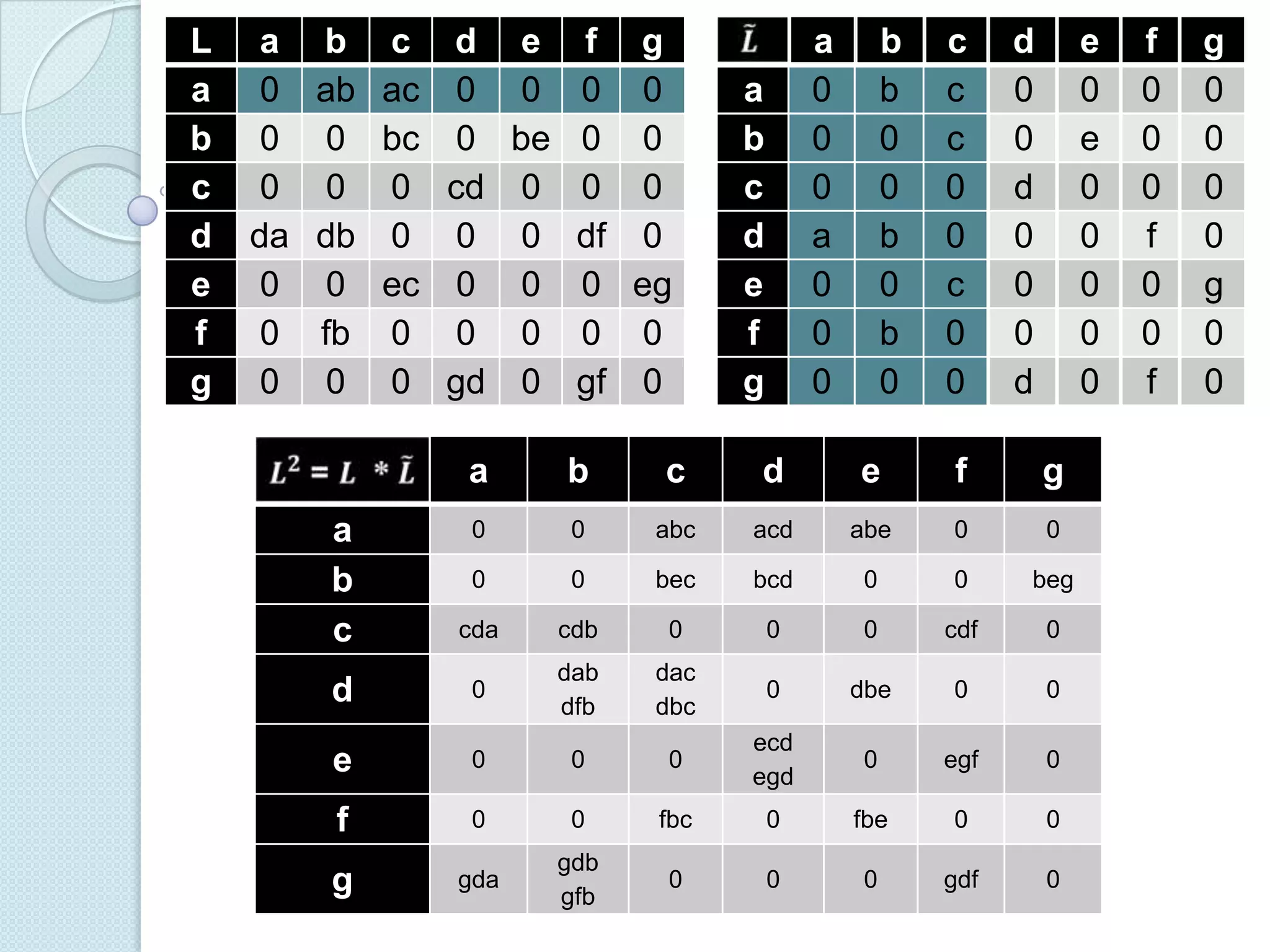
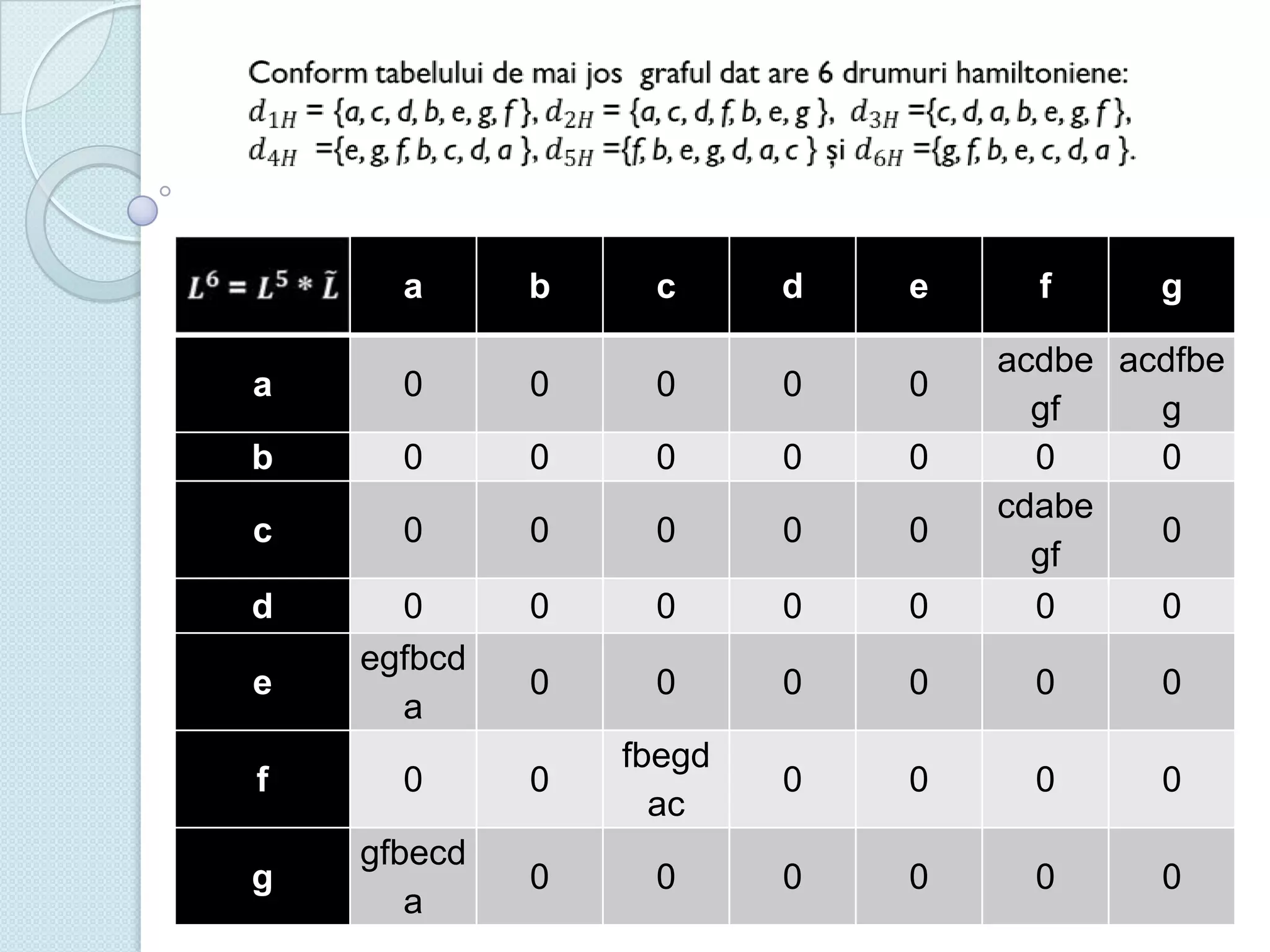
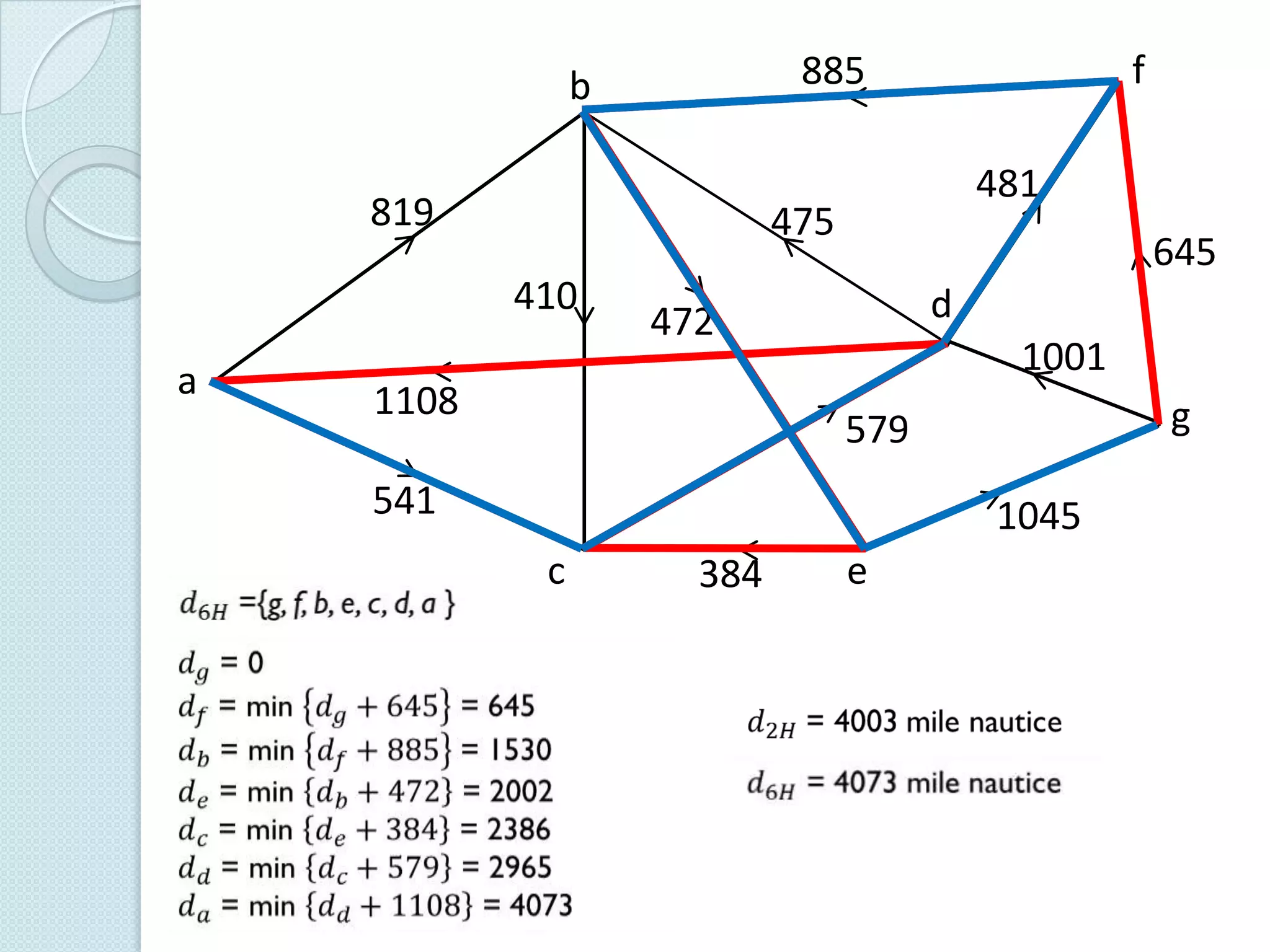
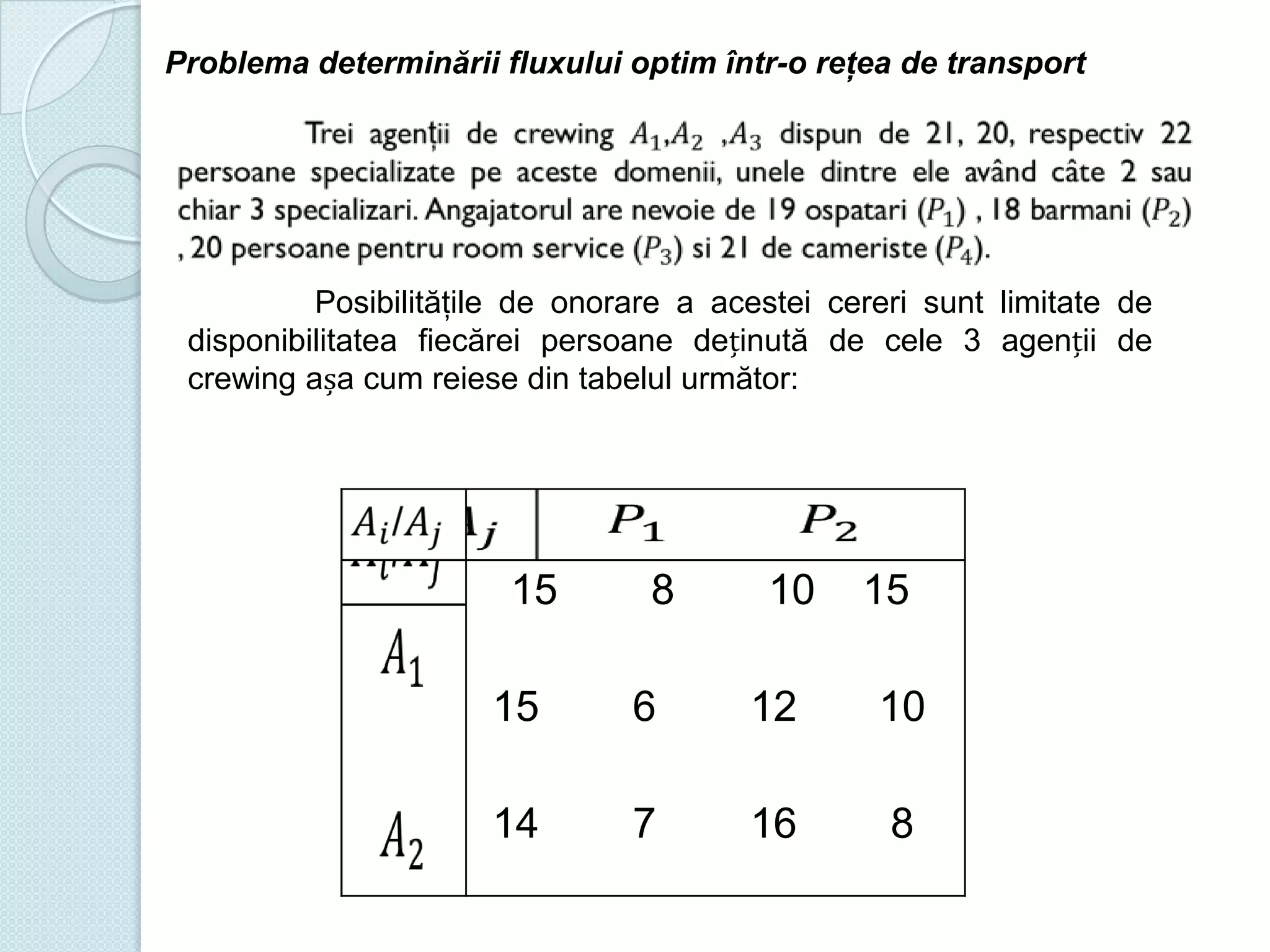
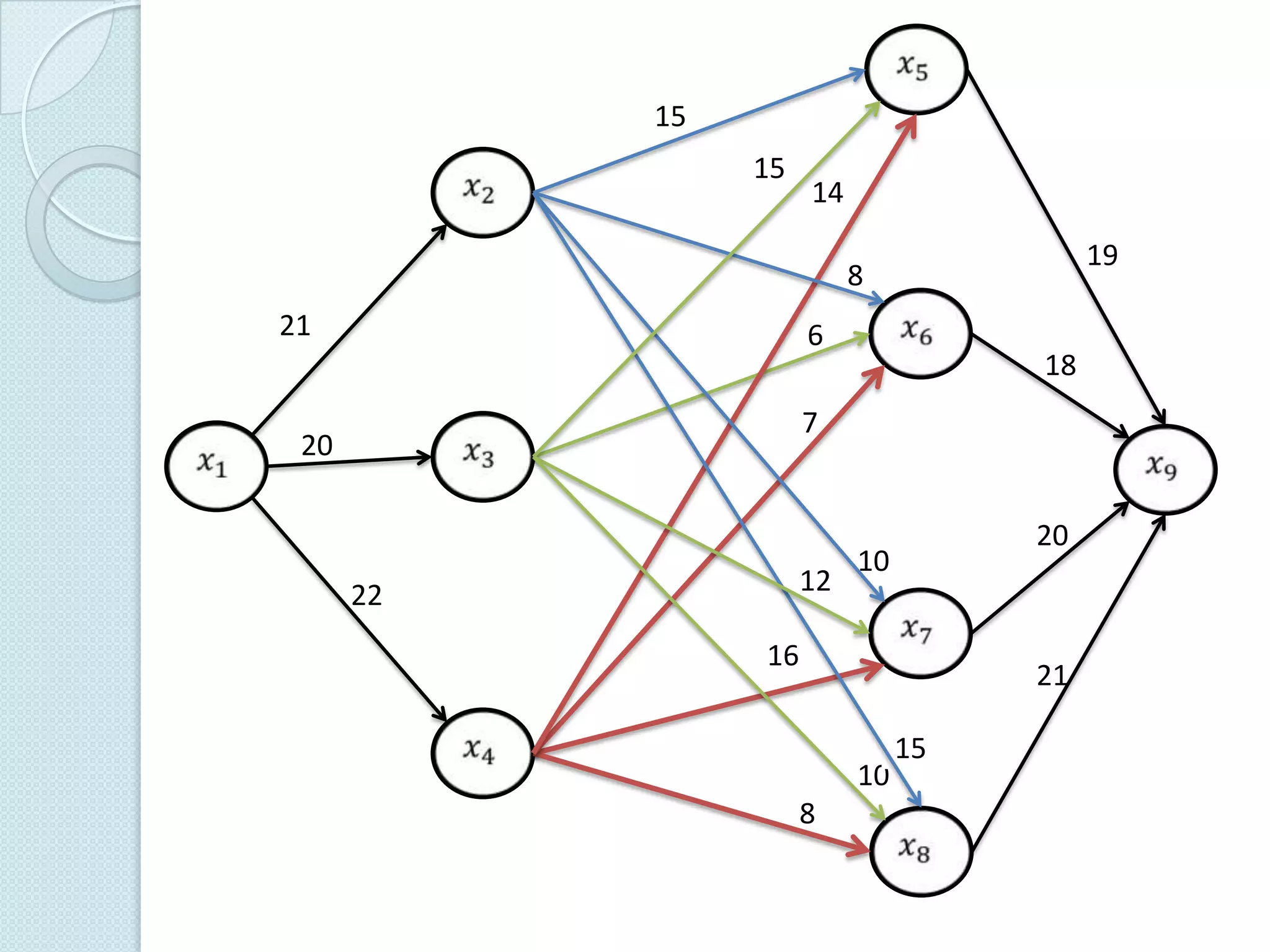
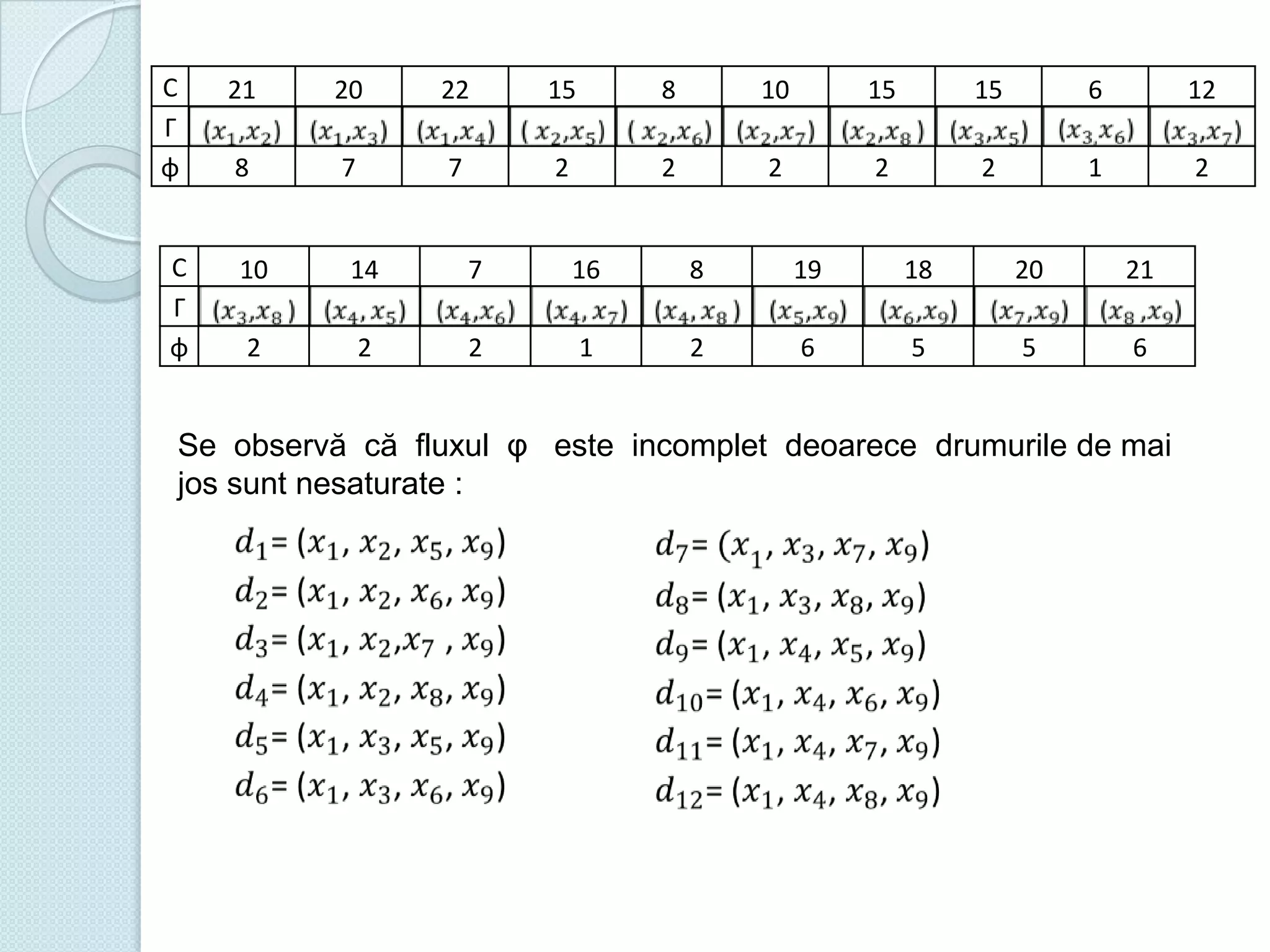
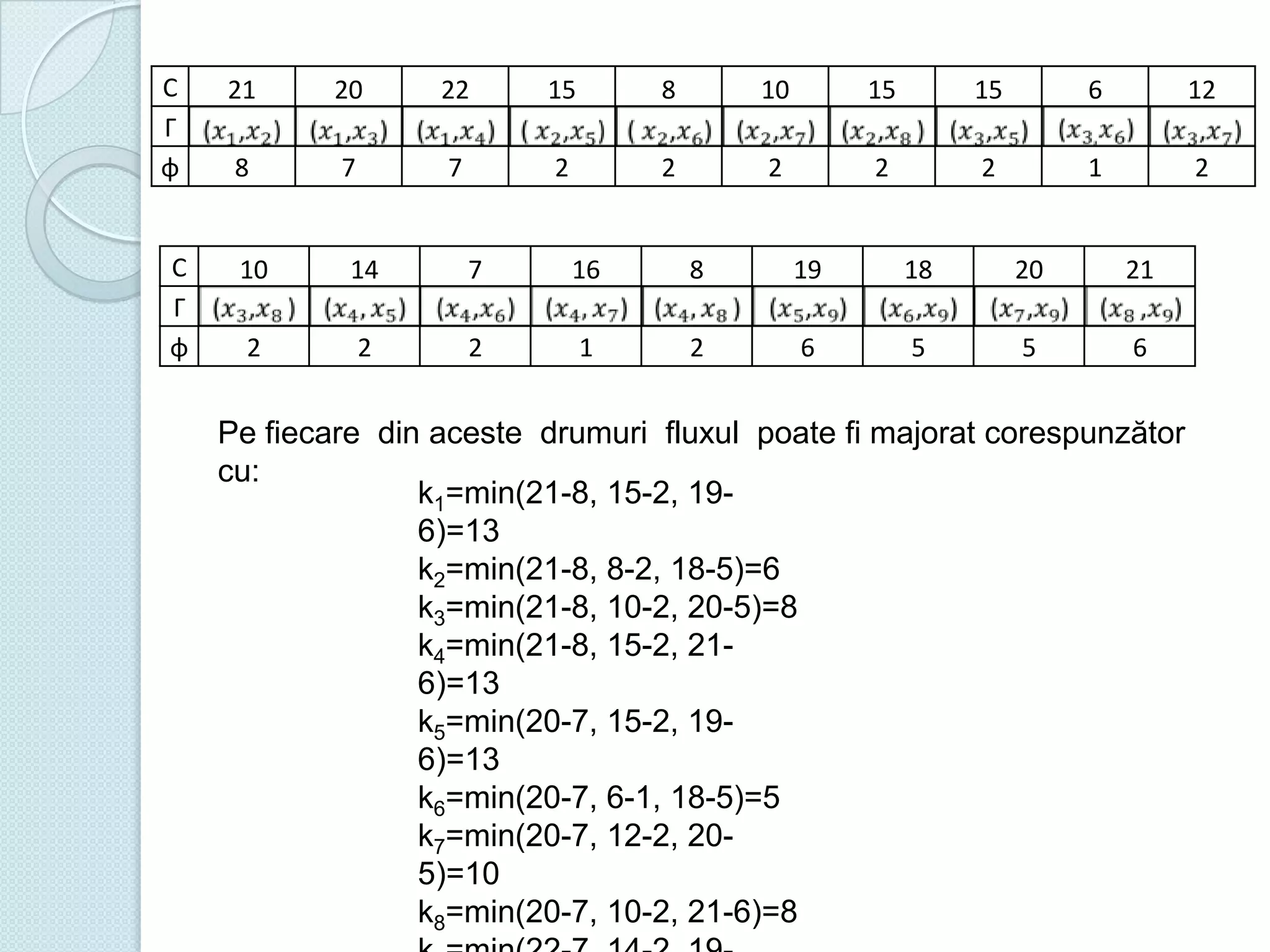
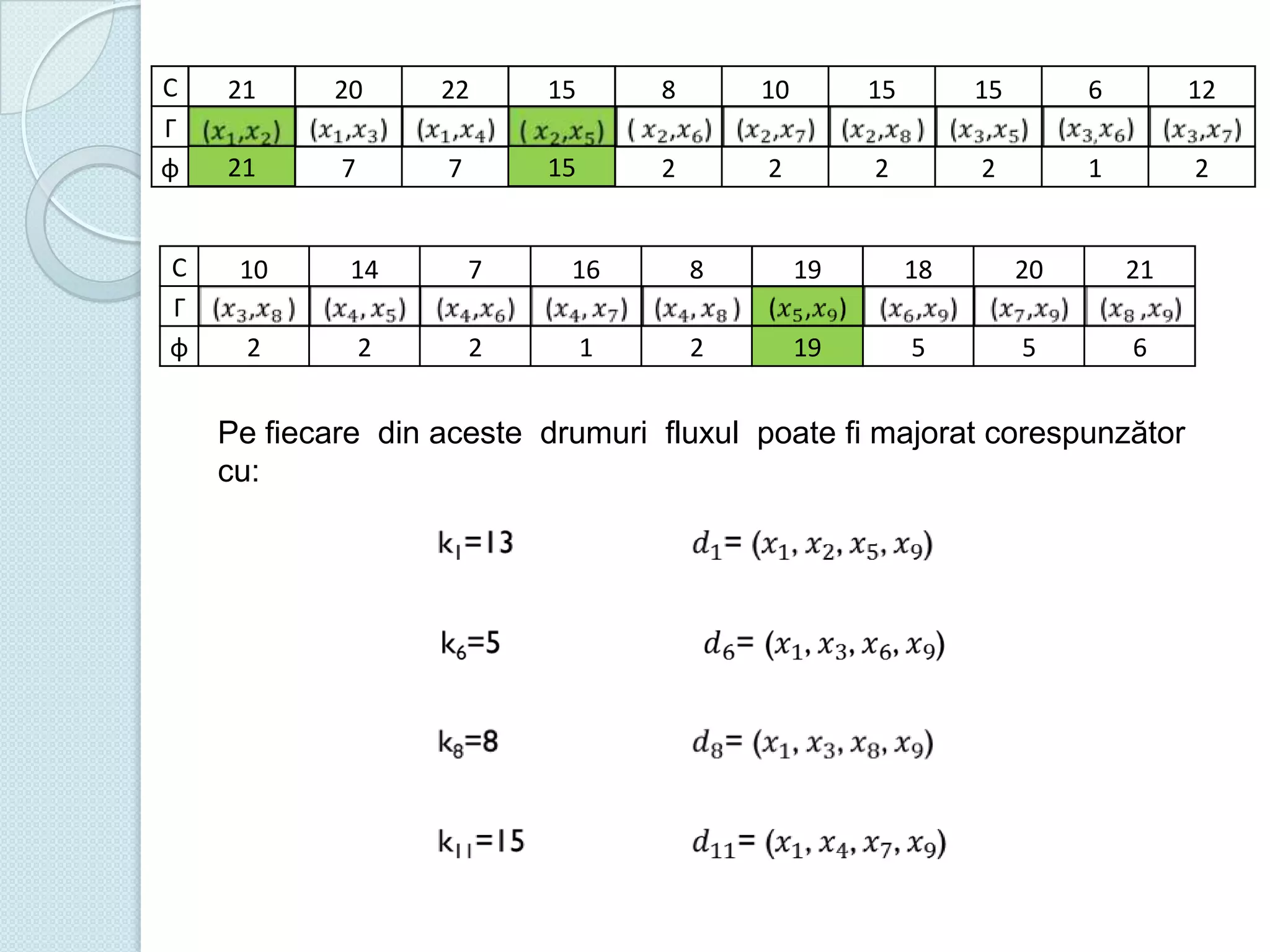
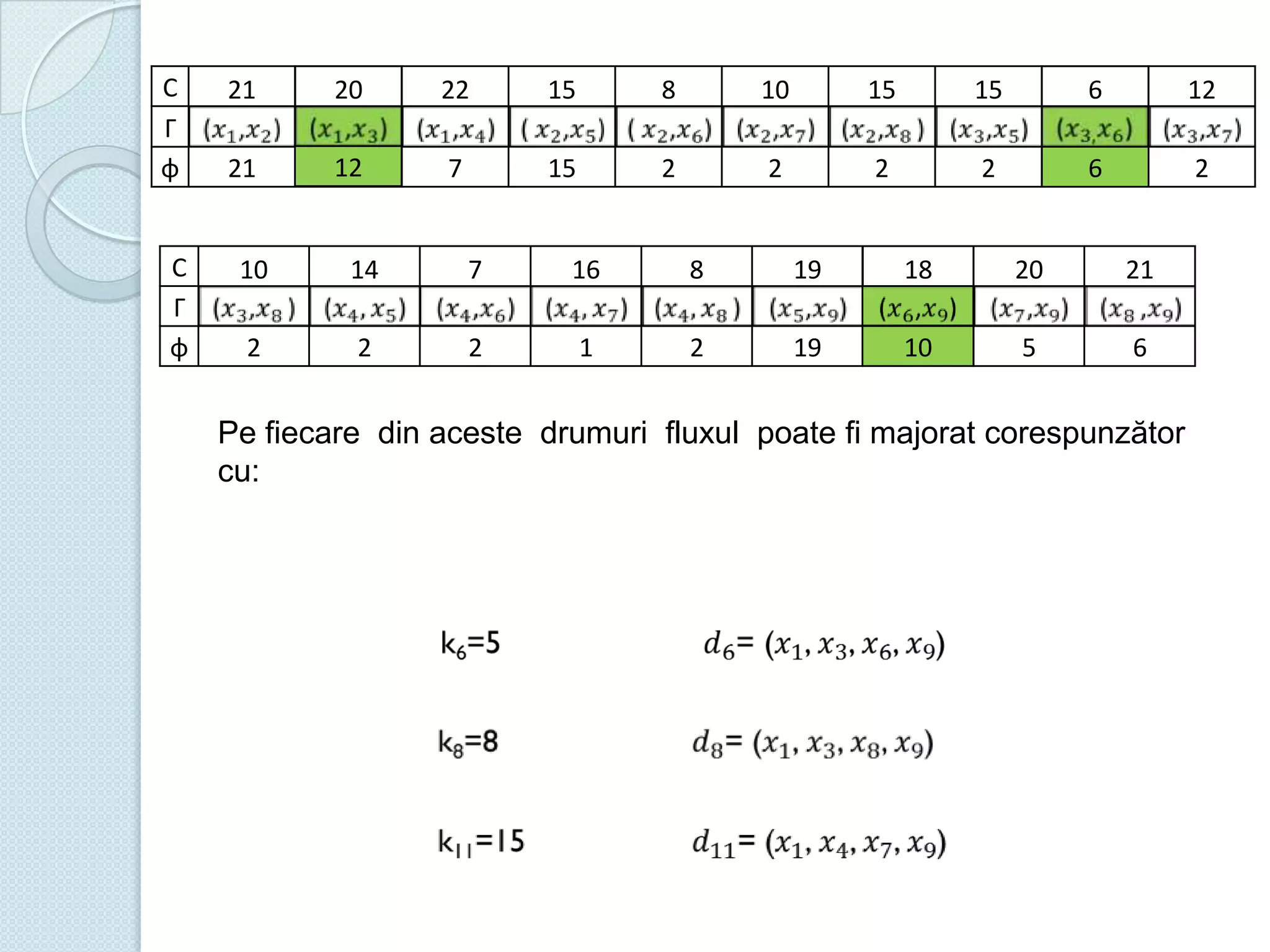
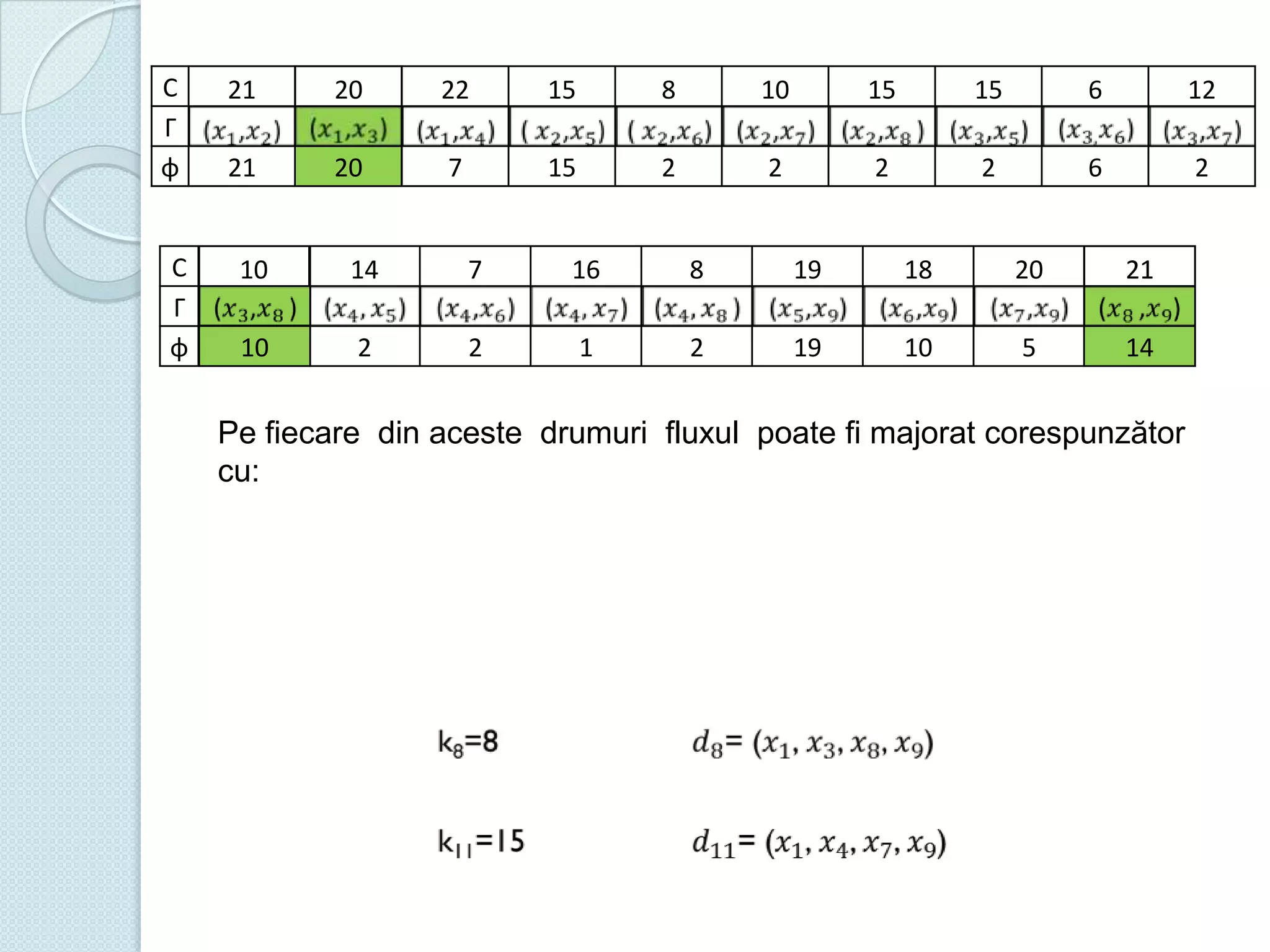
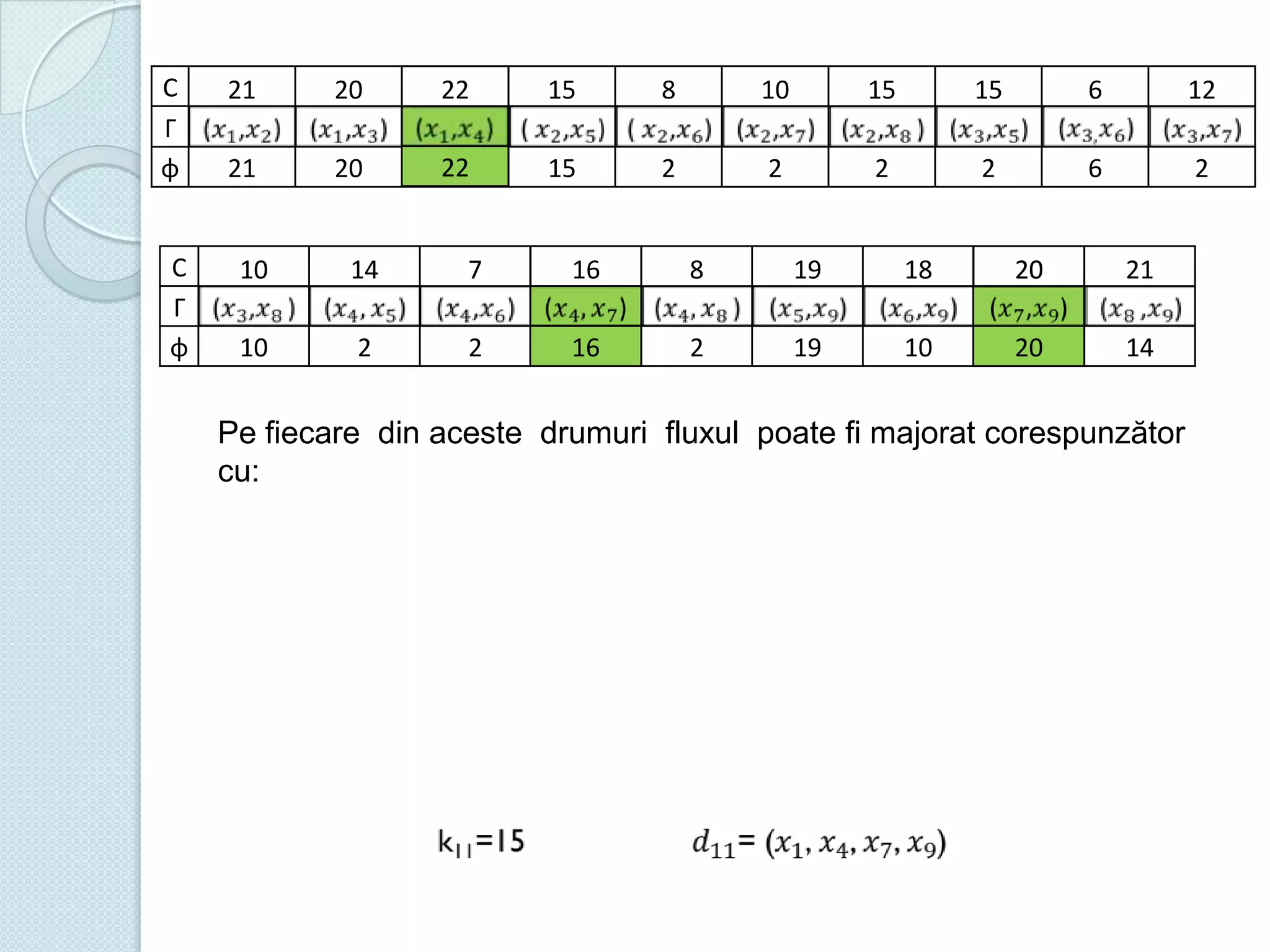
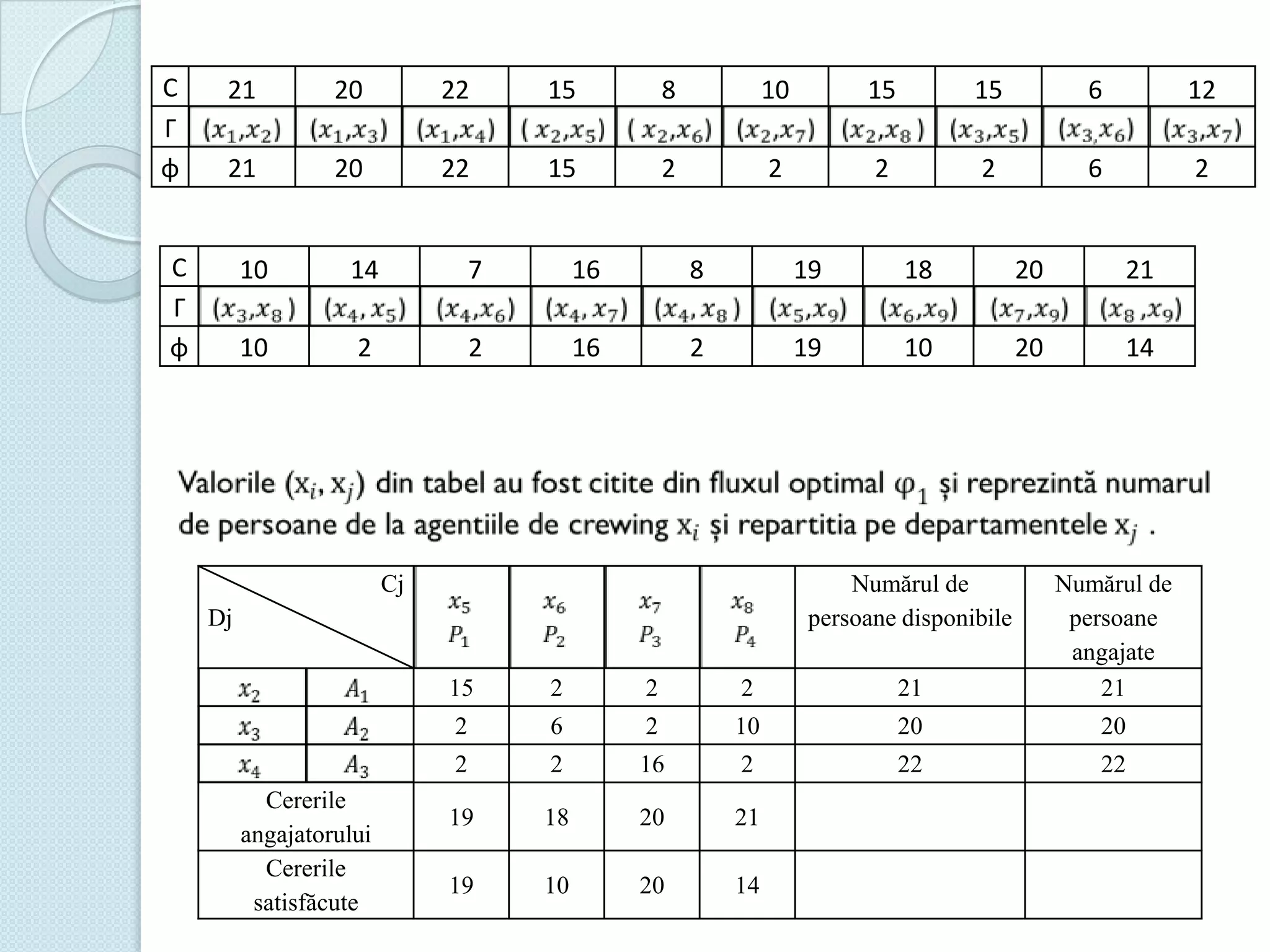
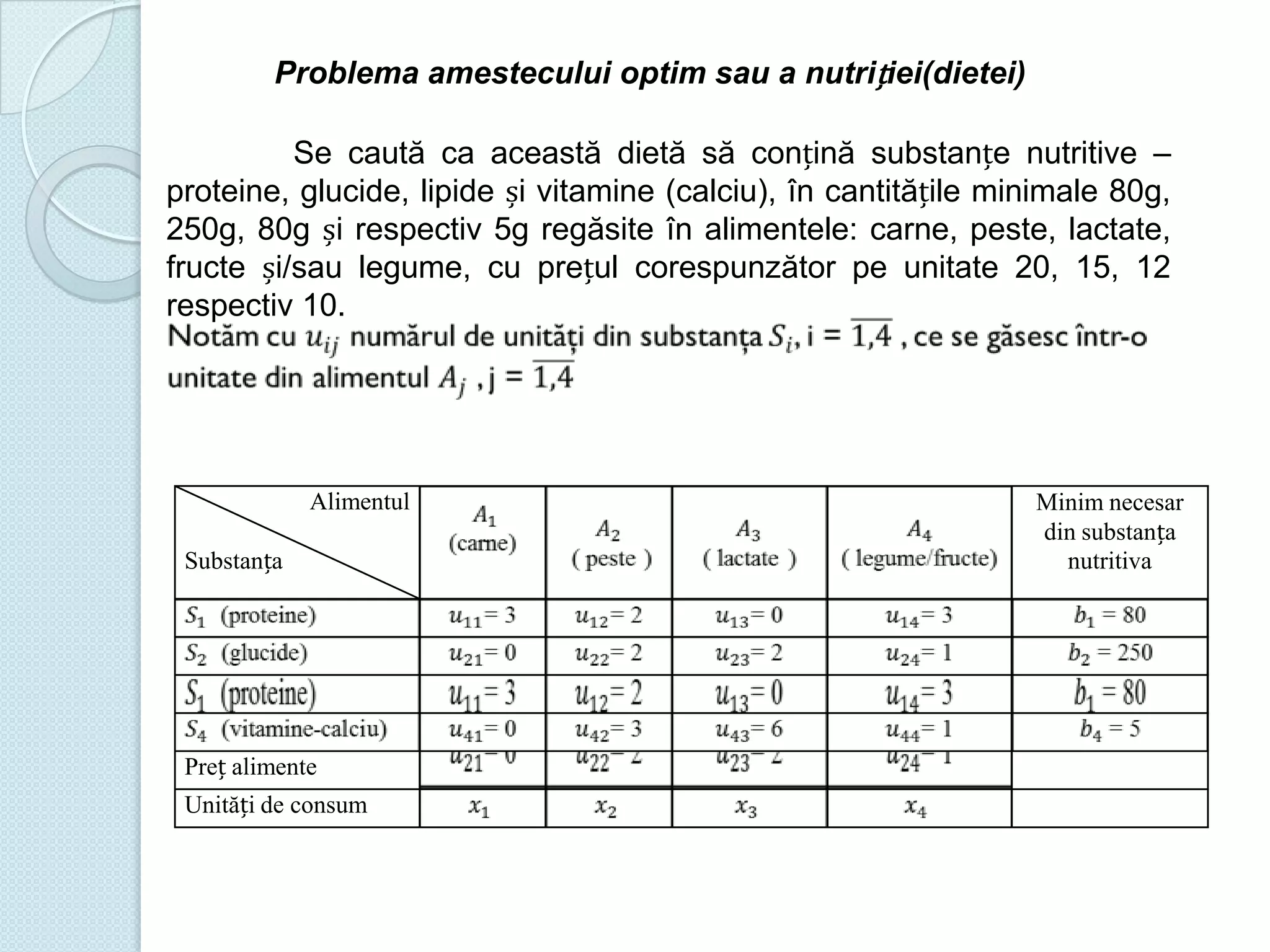
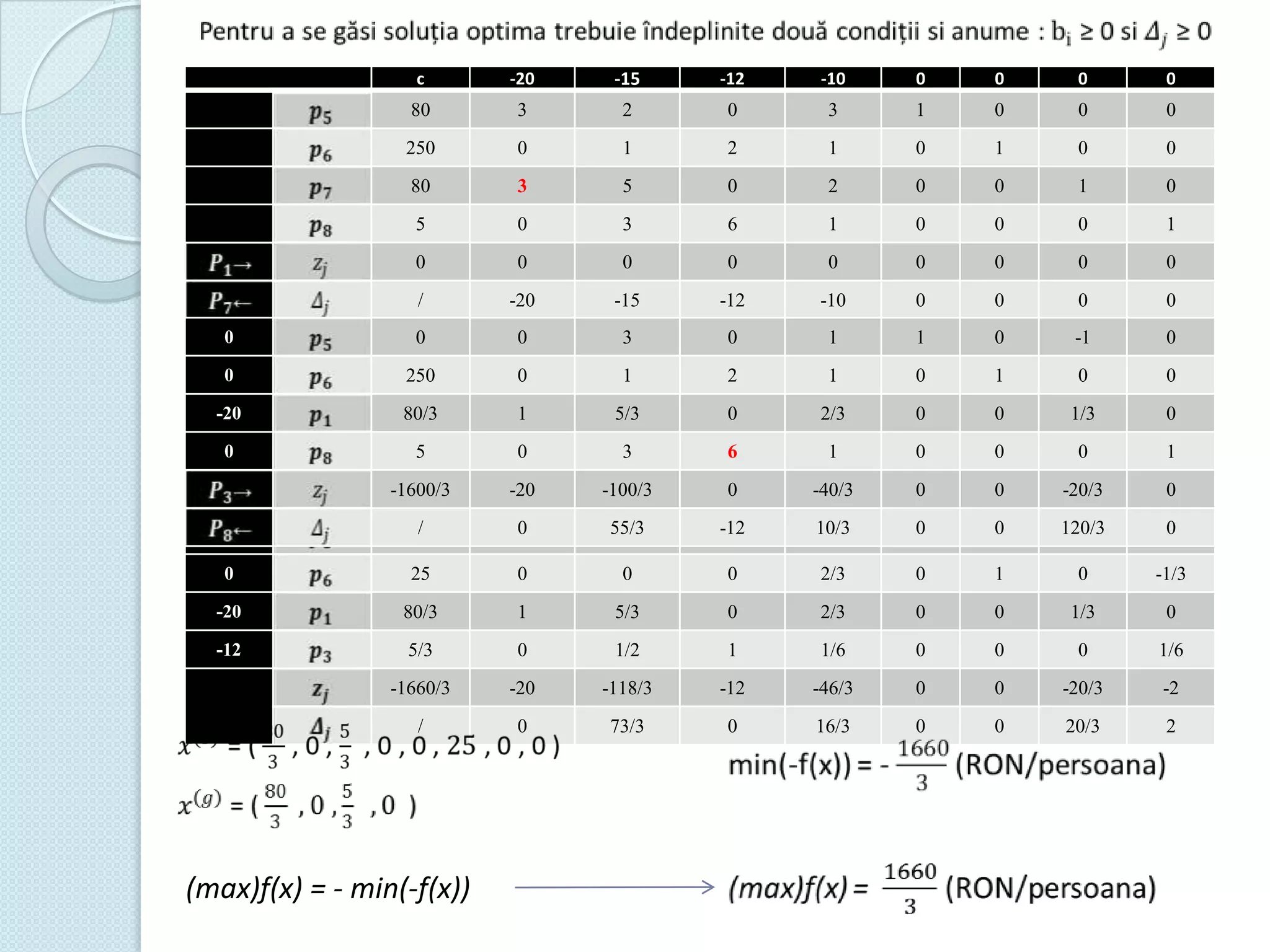
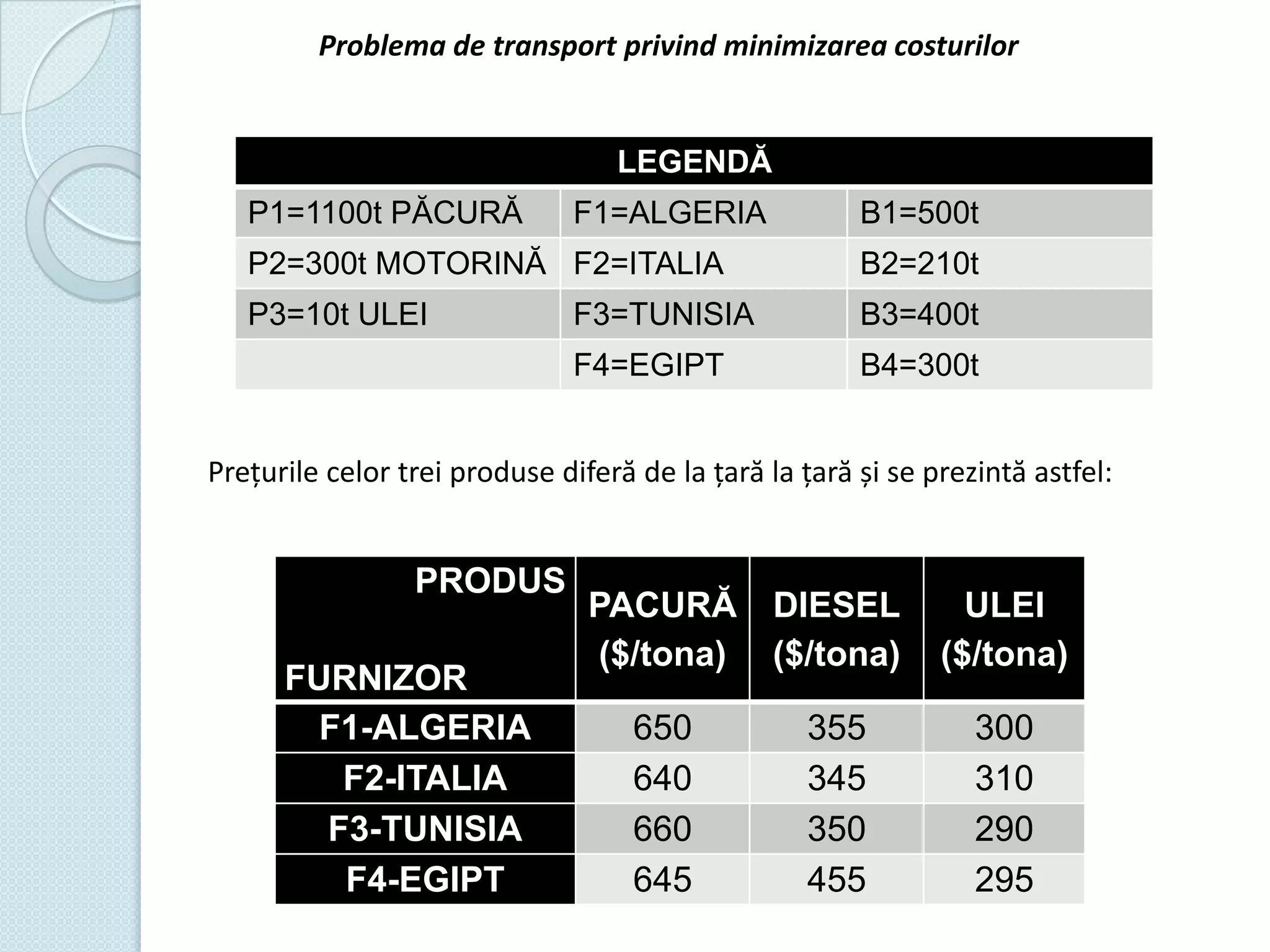
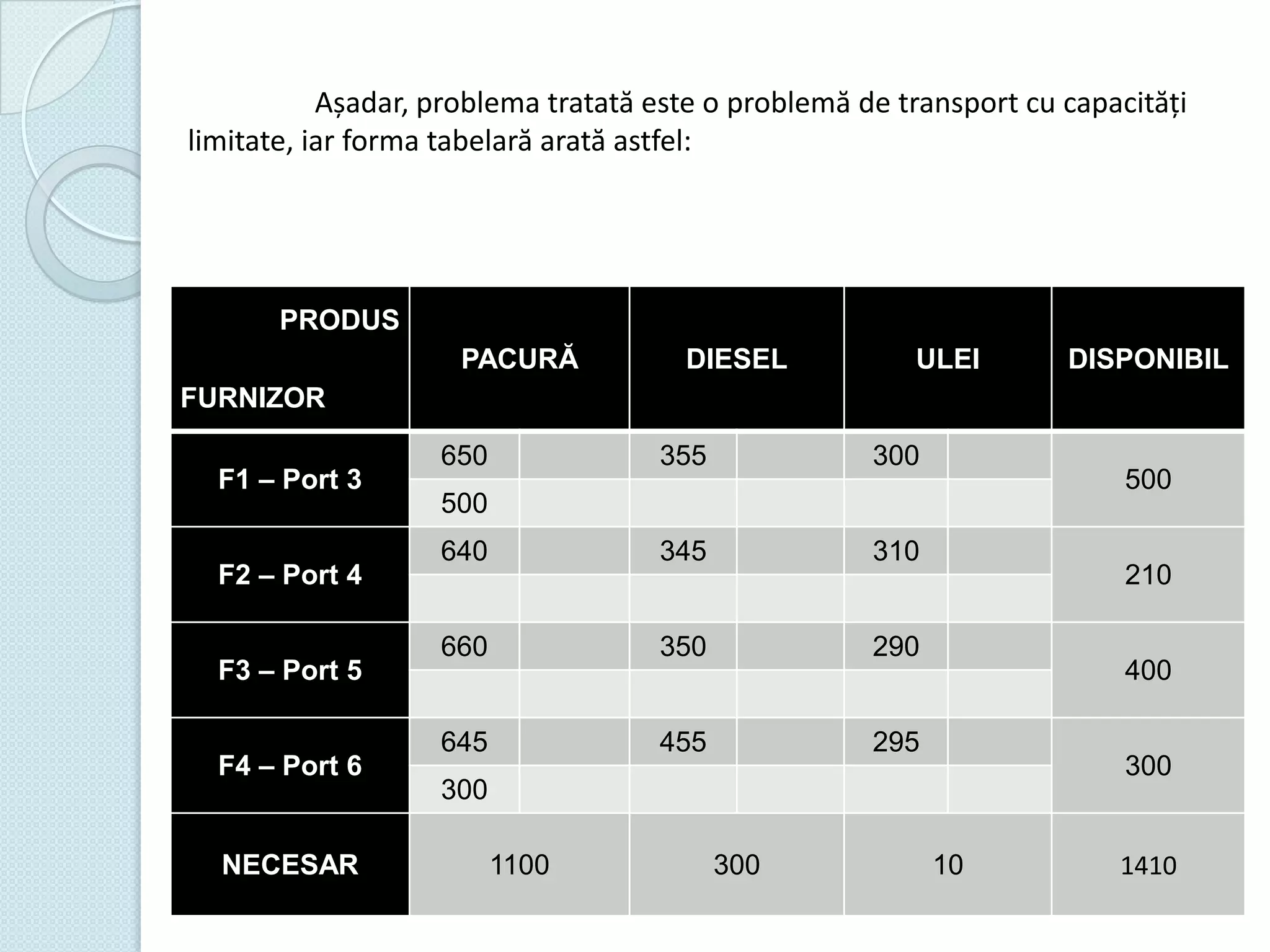
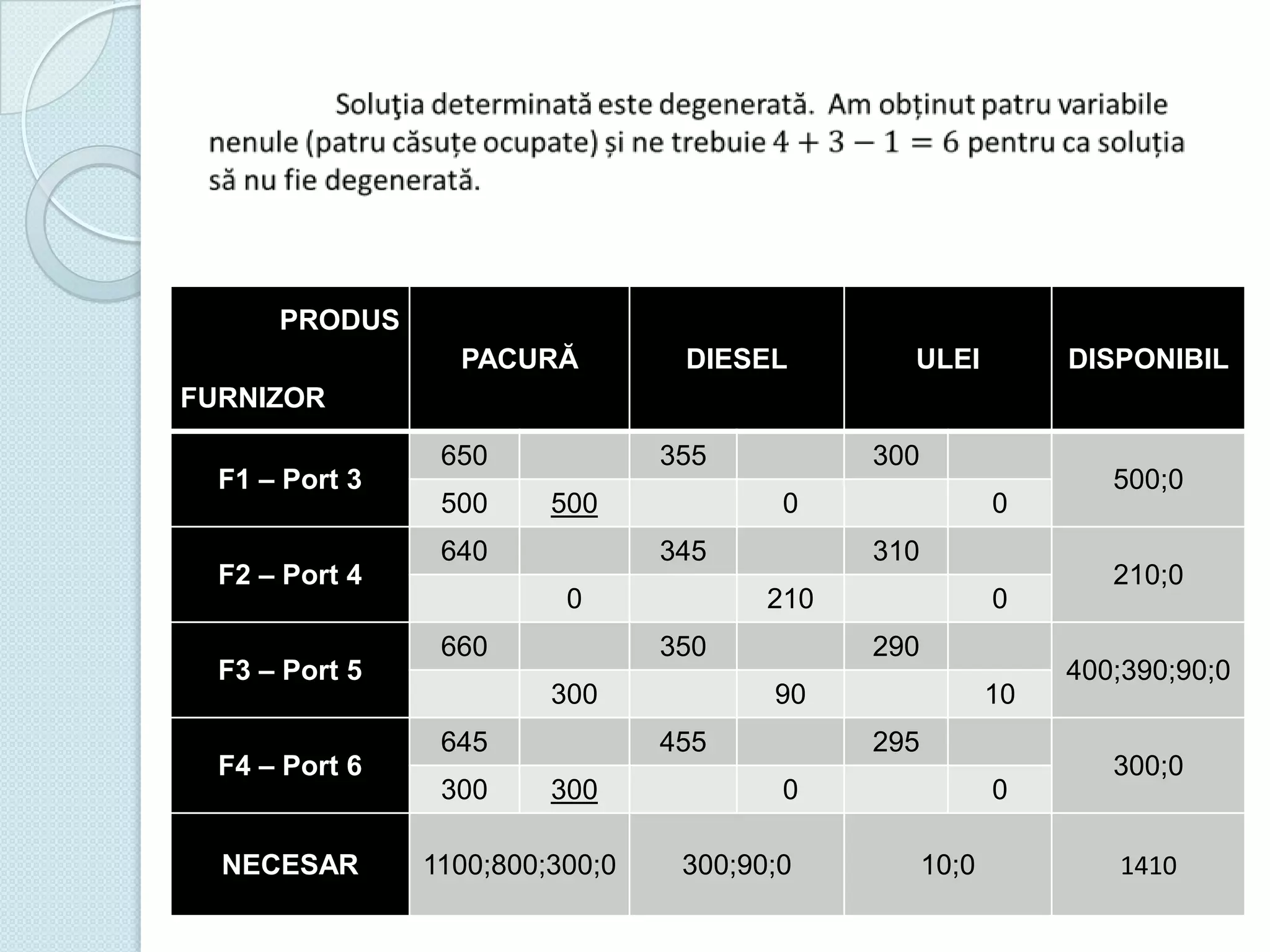
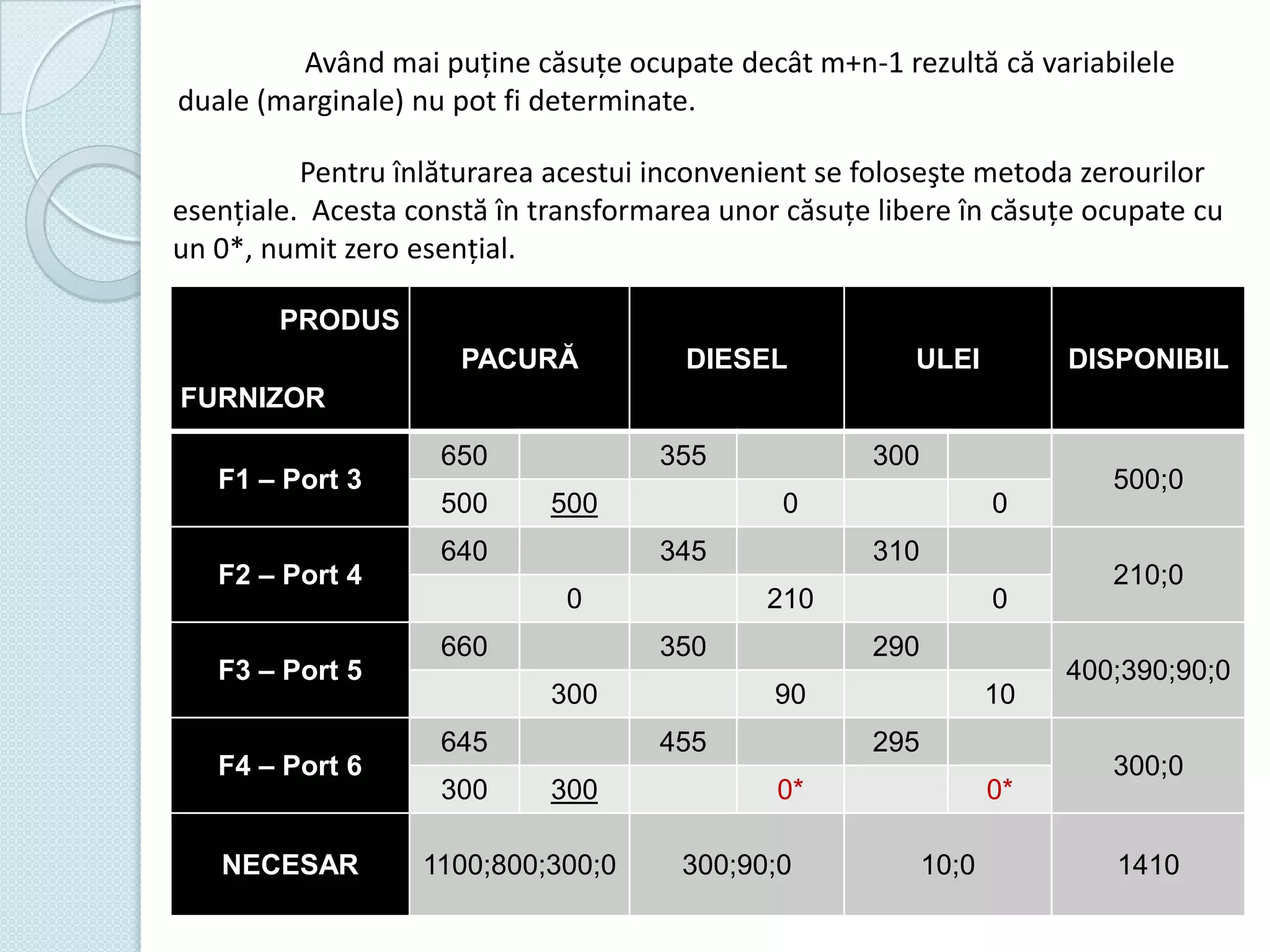
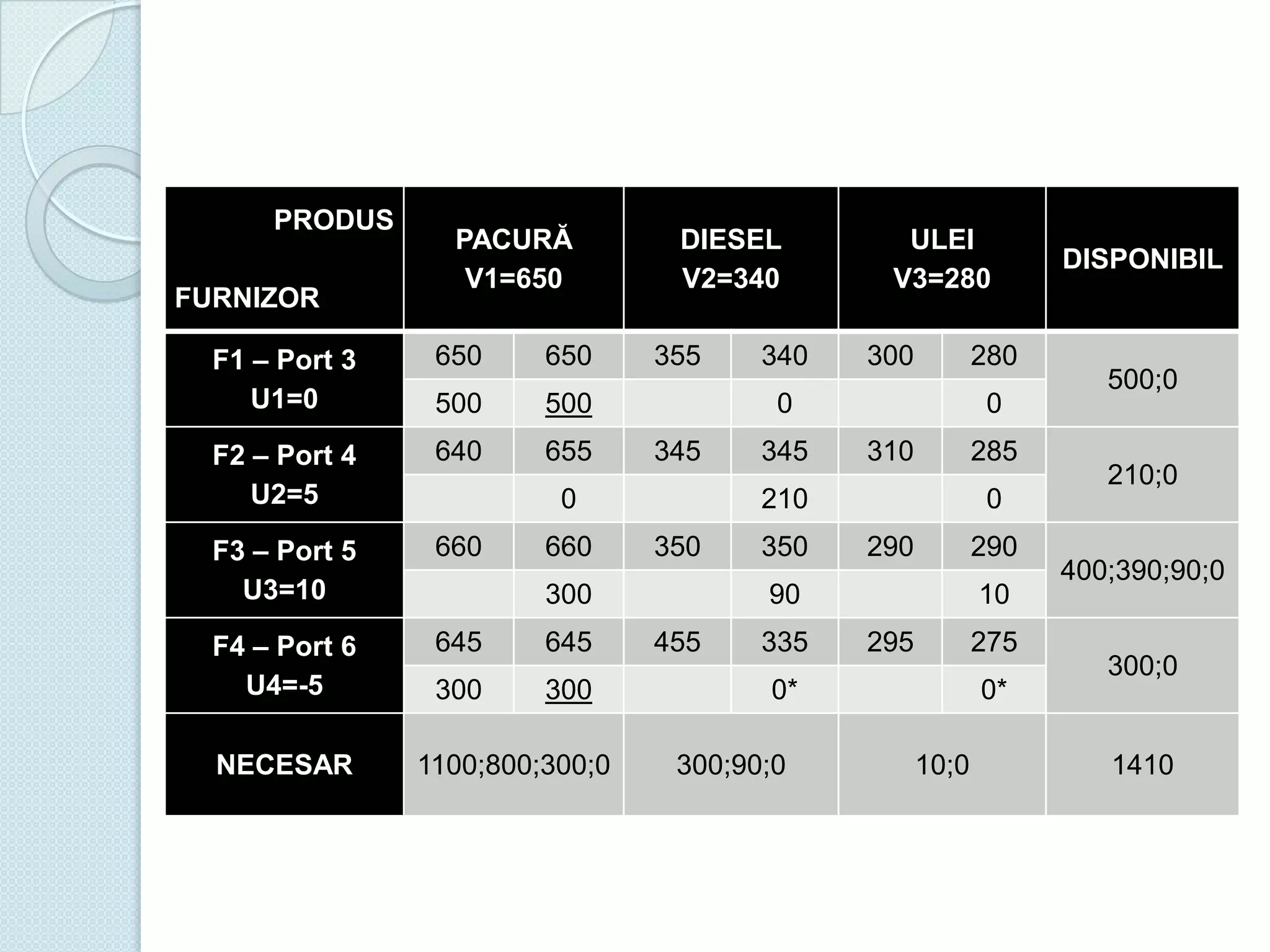
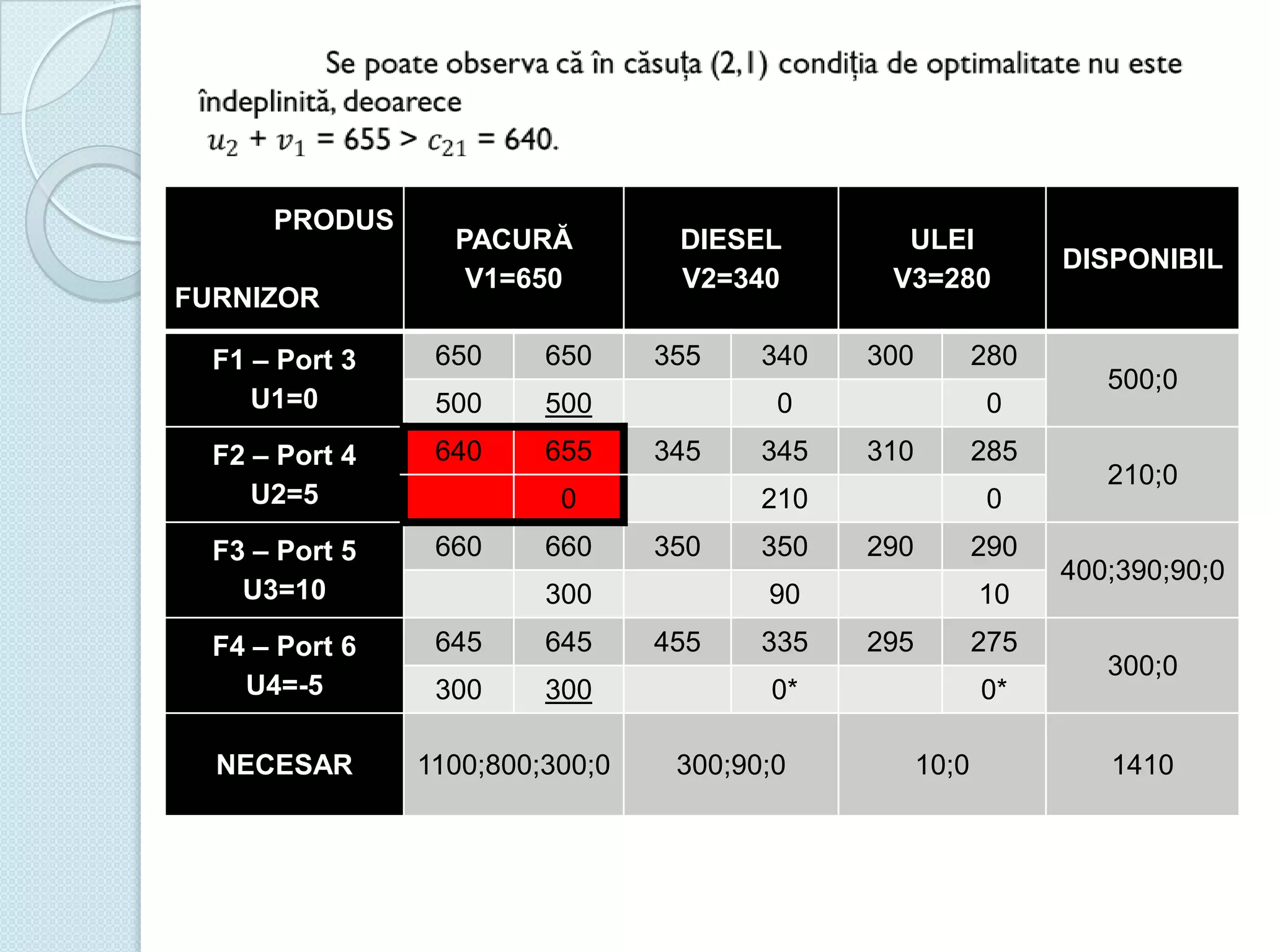
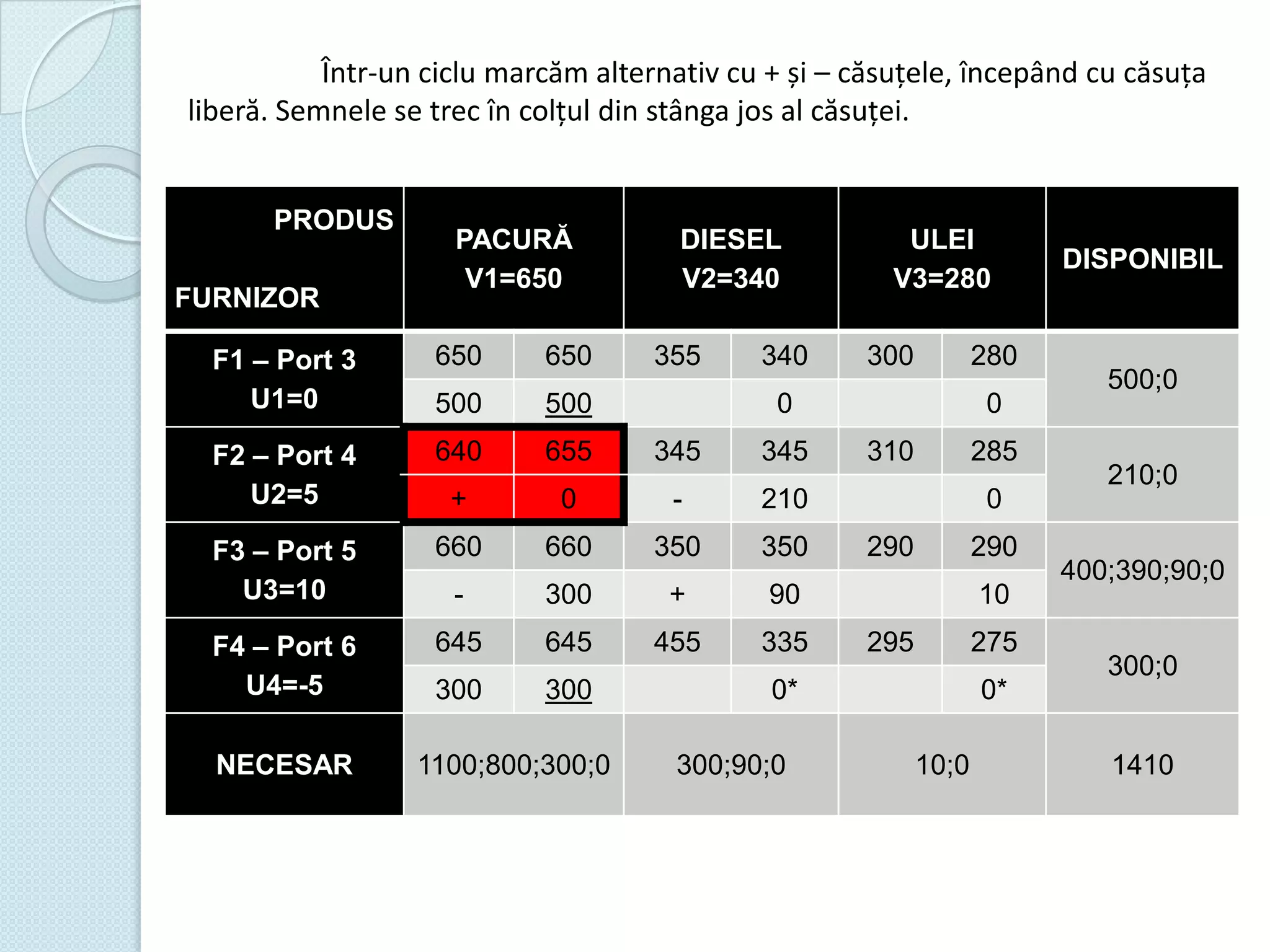
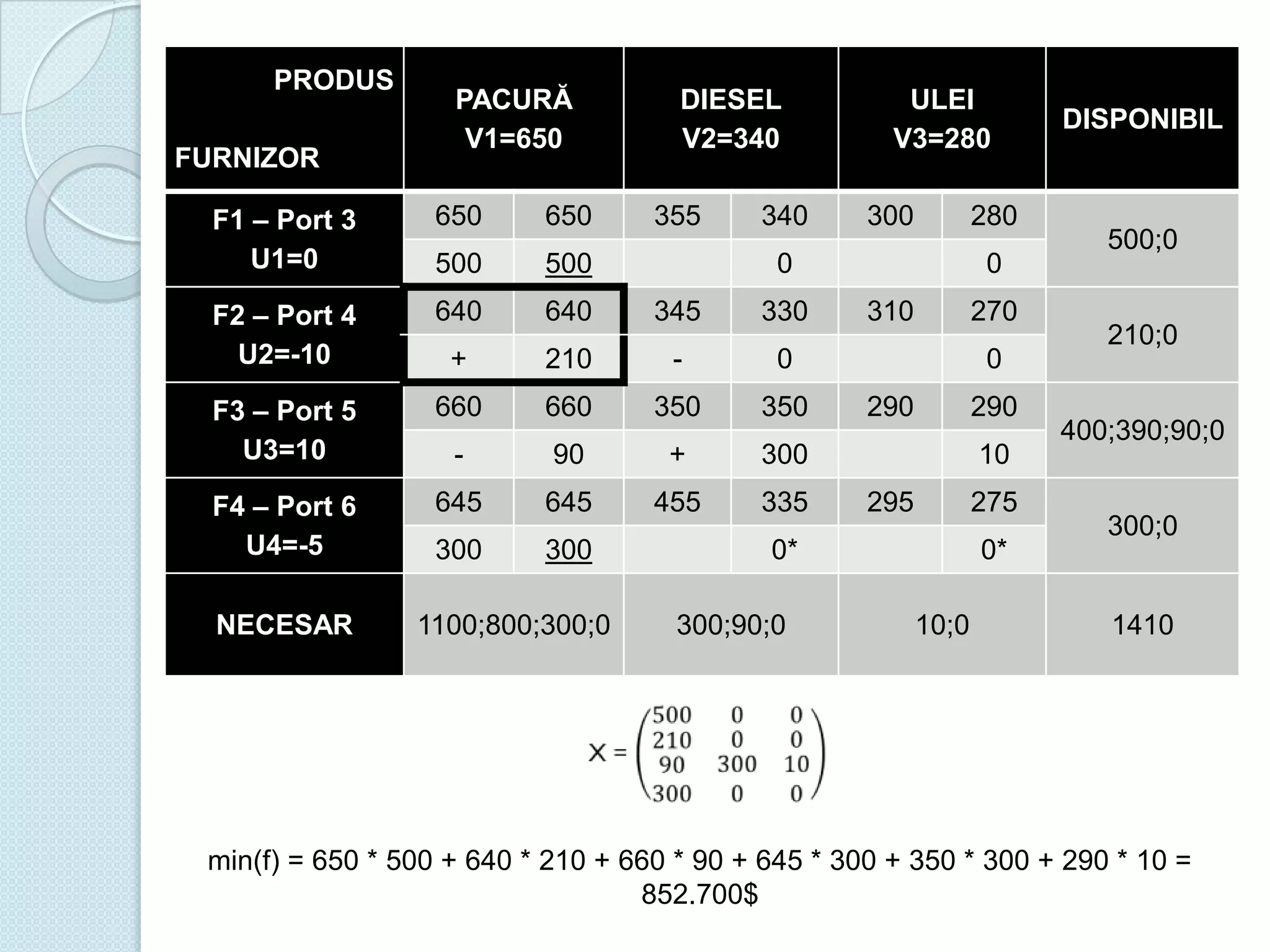
Documentul discută utilizarea metodelor matematice în practica navală, subliniind importanța construirii și studiului modelelor matematice în soluționarea problemelor tehnice și economice. Un studiu de caz analizat se concentrează pe fluxul optim în rețelele de transport, prezentând metode de maximizare a fluxului într-un sistem de transport utilizând echivalentul de resurse disponibile. De asemenea, se investighează problema optimizării amestecului nutritiv și minimizarea costurilor de transport pentru diverse produse, incluzând metodologia de aplicare a modelelor matematice în aceste contexte.