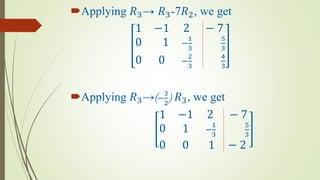The document discusses linear combinations and linear independence of vectors and functions. It defines a linear combination of vectors as a vector that can be expressed as a sum of scalar multiples of other vectors. A set of vectors is linearly dependent if one vector can be written as a linear combination of the others. A set is linearly independent if the only solution to the equation involving scalar multiples of the vectors is when all scalars are zero. It also discusses the Wronskian and its use in determining linear independence of functions. Examples are provided to illustrate these concepts.

1. VECTOR SPACES

2. LINEAR COMBINATION

3. DEFINITION:
A vector v is called a linear combination of vectors
𝑣1, 𝑣2, … … . . , 𝑣 𝑛if there exist scalars 𝑘1, 𝑘2, … … … , 𝑘 𝑛 such that,
𝑣= 𝑘1 𝑣1+𝑘2 𝑣2+……+𝑘 𝑛 𝑣 𝑛
For an example, Type equation here.a vector (a,b)Є𝑅2
is a linear
combination of (1,0)and (0,1) as it can be expressed as
(a,b)=a(1,0)+b(0,1).

4. WORKING RULES :
To check weather a vector 𝑣 is a linear combination of
vectors 𝑣1, 𝑣2, … … . . , 𝑣 𝑛, we have the following method:
Suppose that 𝑣= 𝑘1 𝑣1+𝑘2 𝑣2+……+𝑘 𝑛 𝑣 𝑛 .
Compare the corresponding components to get a linear
system in 𝑘1, 𝑘2, … … … , 𝑘 𝑛.

5. Solve the linear system by the usual methods(Gauss
elimination or Gauss Jordan elimination.)
If the system is consistent, then v is a linear
combination of 𝑣1, 𝑣2, … … . . , 𝑣 𝑛. If the system is
inconsistent ,then v is not a linear combination of
𝑣1, 𝑣2, … … . . , 𝑣 𝑛.

6. EXAMPLES
 Example 1:
Check whether the vector v = (2,1,3) is a linear
combination of 𝑣1 = (1,0,1) and 𝑣2 = −1,2,4 .
 Suppose that v = 𝑘1 𝑣1 + 𝑘2 𝑣2. This is
(2,1,3) = 𝑘1(1,0,1) + 𝑘2(-1,2,4)
(2,1,3) = (𝑘1 − 𝑘2, 2𝑘2, 𝑘1+4𝑘2).
 Comparing the corresponding components,
𝑘1 - 𝑘2 = 2 , 2𝑘1 = 1 , 𝑘1 + 4𝑘2 = 3

7.  The augmented matrix for the system is
1 −1 2
0 2 1
1 4 3
 Applying the operation 𝑅3→𝑅3 − 𝑅1 , we obtain
1 −1 2
0 2 1
0 5 1
 Applying the operation 𝑅2 →(1 2)𝑅2, we obtain
1 −1 2
0 1 1
2
0 5 1

8.  Applying the operation 𝑅3 → 𝑅3 - 5𝑅2, we obtain
1 −1 2
0 1 1
2
0 0 −3
2
 From the last row of the above matrix, we get 0 =
−3
2
, which is not possible. Thus the system is
inconsistent and hence v is not a linear
combination of 𝑣1 and 𝑣2.

9.  Example 2
Express the polynomial p(x) = -9-7x-15𝑥2
as a
linear combination of 𝑝1(x) = 2 + x + 4𝑥2
, 𝑝2(x) = 1
– x + 3𝑥2
, 𝑝3(x) = 3 + 2x + 5𝑥2
.
 Suppose that p(x) = 𝑘1 𝑝1(x) + 𝑘2 𝑝2(x) + 𝑘3 𝑝3(x).
-9 – 7x -15𝑥2
= 𝑘1(2+x+4𝑥2
) + 𝑘2(1-x+3𝑥2
) +
𝑘3(3+2x+5𝑥2
)
-9 – 7x -15𝑥2
= (2𝑘1+𝑘2+3𝑘3) + (𝑘1 − 𝑘2+2𝑘3)x
+ (4𝑘1+3𝑘2+5𝑘3)𝑥2

10.  Equating the corresponding coefficients of 1,x and
𝑥2
on both sides, we get
2𝑘1 + 𝑘2 + 3𝑘3 = -9
𝑘1 - 𝑘2 + 2𝑘3 = -7
4𝑘1 + 3𝑘2 + 5𝑘3 = -15
 The augmented matrix of the system is

2 1 3 − 9
1 −1 2 − 7
4 3 5 − 15

11.  Applying 𝑅1↔𝑅2, we get
1 −1 2 − 7
2 1 3 − 9
4 3 5 − 15
 Applying 𝑅2→ 𝑅2-2𝑅1 and 𝑅3→ 𝑅3-4𝑅1,we get
1 −1 2 − 7
0 3 −1 5
0 7 −3 13
 Applying 𝑅2 → (1
3
) 𝑅2, we get
1 −1 2 − 7
0 1 − 1
3
5
3
0 7 −3 13

12. Applying 𝑅3→ 𝑅3-7𝑅2, we get
1 −1 2 − 7
0 1 −
1
3
5
3
0 0 −
2
3
4
3
Applying 𝑅3→(−
3
2
) 𝑅3, we get
1 −1 2 − 7
0 1 −
1
3
5
3
0 0 1 − 2

13. Which is row echelon form. The system
corresponding to the last matrix is
𝑘1-𝑘2+2𝑘3= -7
𝑘2- 1
3
𝑘3 =5
3
𝑘3 = -2
Using back substituting, we get
𝑘1=-2, 𝑘2=1, 𝑘3=-2
Hence
P(x)=-2𝑝1(𝑥)+𝑝2(𝑥)-2𝑝3 𝑥 .

14. Example :3
Check weather the vector v=(0,4,5)is a linear
combination of 𝑣1=(0,-2,2) and 𝑣2=(1,3,-1) ?
Solution :
Suppose that 𝑣=𝑘1 𝑣1+𝑘2 𝑣2
that is (0,4,5)=𝑘1(0,-2,2)+𝑘1(1,3,-1)
(0,4,5)=(𝑘2, -2𝑘1+3𝑘2,2𝑘1-𝑘2)
Comparing the corresponding components. We
obtain

15. 𝑘2=0…….1
-2𝑘1+3𝑘2=4…….2
2𝑘1-𝑘2=5……..3
Here 𝑘2=0 so solve the equation 2 and 3 we get
𝑘1=-2 and 𝑘1=5
2
so which is not
possible so 𝑣is not linear combination.

16. SPAN

17. DEFINITION:
Let S= 𝑣1, 𝑣2, … … . . , 𝑣 𝑛 be a set of vectors in a vector space
V. Then the set of all linear combinations of the vectors in S is
called the space spanned by
𝑣1, 𝑣2, … … . . , 𝑣 𝑛. If we denote this set by W then we say
that 𝑣1, 𝑣2, … … . . , 𝑣 𝑛 span W. symbolically,
W=span(S) or W=span 𝑣1, 𝑣2, … … . . , 𝑣 𝑛 .

18. LINEAR
DEPENDENCE&INDEPENDENCE

19. DEFINITION:
The vectors 𝑣1, 𝑣2, … … . . , 𝑣 𝑛 are said to be linear dependent
if there exist scalars 𝑘1, 𝑘2, … … … , 𝑘 𝑛,not all zero such that
𝑘1 𝑣1+𝑘2 𝑣2+……+𝑘 𝑛 𝑣 𝑛 =0
And linearly independent if,
𝑘1 𝑣1+𝑘2 𝑣2+……+𝑘 𝑛 𝑣 𝑛 =0 => 𝑘1=𝑘2=……..=𝑘 𝑛=0.

20. THEOREMS:
1)Let S= 𝑣1, 𝑣2, … … . . , 𝑣 𝑛 be a set of n vectors. Then S is
linearly dependent if and only if one of the vectors in S can be
expressed as a linear combination of the other vectors in S.
2) A set of two vectors is linearly dependent if and only if
one vector is a scalar multiple of the other.
.

21. 3)A set containing zero vector is linearly dependent.
4)If 𝑣1, 𝑣2, … … . . , 𝑣 𝑘 are vectors in 𝑅 𝑛
and k>n , then the
vectors are linearly dependent

22. WRONSKIAN
Let 𝑓1(𝑥) , 𝑓2(𝑥),… 𝑓𝑛(𝑥) be n-1 times
continuously differentiable function of the
interval (-∞,∞). Then
 W 𝑥 =
𝑓1(𝑥) 𝑓2 𝑥 … . . 𝑓𝑛(𝑥)
𝑓′1(𝑥) 𝑓′
2
𝑥 … … 𝑓′ 𝑛(𝑥)
.
.
.
𝑓
(𝑛−1)
1
.
.
.
𝑓
(𝑛−1)
2
.
.
.
𝑓
(𝑛−1)
𝑛
Is called the Wronskian of the functions
𝑓1(𝑥) , 𝑓2(𝑥),… 𝑓𝑛(𝑥).

23. LINEAR INDEPENDENCE OF
FUCTION:
Let 𝑓1 x , 𝑓2 𝑥 , … … … , 𝑓𝑛 𝑥 be n-1 times continuously
differentiable functions on the interval (−∞, ∞).If the
wronskian of these function is nonzero for at least one point
in this interval , then these functions are linearly independent
in 𝐶(𝑛−1)
(−∞, ∞).

24. EXAMPLES
 Examples : 1
Let 𝑣1=(1,-1,0), 𝑣2=(0,1,-1) and 𝑣3=(0,0,1) be element in 𝑅3
.
Show that the set of vector {𝑣1, 𝑣2, 𝑣3} is linearly independent.
 Solution : We consider the vector equation
𝑘1 𝑣1+ 𝑘 𝑣2 + 𝑘 𝑣3 = 0
substituting for 𝑣1, 𝑣2, 𝑣3, we obtain
𝑘1(1,-1,0) + 𝑘2(0,1,-1) + 𝑘3(0,0,1)=0
(𝑘1,-𝑘1+𝑘2,-𝑘2+𝑘3)=0

25. Comparing we obtain
𝑘1=0, -𝑘1+𝑘2=0 and -𝑘2+𝑘3=0
The solution of these equation is 𝑘1=𝑘2=𝑘3=0.
Therefore , the given set of vectors is lineary
independent.
 Alternative
det(𝑣1,𝑣2,𝑣3)=
1 0 0
−1 1 0
0 −1 1
= 1 ≠ 0.
Therefore , the given vectors is linearly
independent.

26. Example : 2
Let 𝑣1=(1,-1,0), 𝑣2=(0,1,-1), 𝑣3=(0,2,1) and 𝑣4=(1,0,3) be
element of 𝑅3. Show that the set of vector {𝑣1, 𝑣2, 𝑣3, 𝑣4} is
linearly dependent.
Solution : The given set of element will be dependent if
there exists scalar 𝑘1, 𝑘2, 𝑘3, 𝑘4 not all zero, such that
𝑘1 𝑣1+ 𝑘2 𝑣2+ 𝑘3 𝑣3+ 𝑘4 𝑣4=0
Substituting for 𝑣1, 𝑣2, 𝑣3, 𝑣4 and comparing, we obtain
𝑘1+ 𝑘4=0, -𝑘1+ 𝑘2+2 𝑘3=0,- 𝑘2+ 𝑘3+3 𝑘4=0

27. The solution of this equation is
𝑘1=- 𝑘4, 𝑘2=
5𝑘4
3
, 𝑘3=−
4𝑘4
3
, 𝑘4 arbitrary.
Substituting equation (1) and cancelling 𝑘4, we
obtain
- 𝑣1+
5
3
𝑣2-
4
3
𝑣3+ 𝑣4=0
Hence there exist scalar not all zero, such that
(1) is satisfied. Therefore, the set of vector is
linearly dependent.

28. Example : 3
Check whether the set S={𝑥 +4𝑥2
,3+6𝑥+2𝑥2
,2+10𝑥-4𝑥2
}
is linearly independent 𝑃2.
Solution : Let 𝑃1(𝑥 )=2-𝑥 +4𝑥2
𝑃2(𝑥 )=3+6𝑥 +2𝑥2
𝑃3 (𝑥 )=2+10𝑥 -4𝑥2
Now, we know that
𝑘1 𝑃1(𝑥)+ 𝑘2 𝑃2(𝑥)+……..+ 𝑘 𝑛 𝑃𝑛(𝑥)=0

29.  𝑘1(2-𝑥 +4𝑥2
)+𝑘2(3+6𝑥 +2𝑥2
)+𝑘3(2+10𝑥 -4𝑥2
)=0+0𝑥 +0𝑥2
(2𝑘1+3𝑘2+2𝑘3) +(-𝑘1+6𝑘2+10𝑘3) 𝑥 +(4𝑘1+2𝑘2-4𝑘3) 𝑥2 = 0+0𝑥 +0𝑥2
Equating the corresponding coefficient of 𝑥2, 𝑥 ,1 on both the sides,
we get
2𝑘1+3𝑘2+2𝑘3=0
-𝑘1+6𝑘2+10𝑘3=0
4𝑘1+2𝑘2-4𝑘3=0

30. The coefficient of the matrix of the system
A=
2 3 2
−1 6 10
4 2 −4
det(A)=2(-24-20)-3(4-40)+2(-2-24)
= -88+108-52=-32≠0
Hence , the 𝑃1(𝑥 ), 𝑃2(𝑥 ) and 𝑃3(𝑥 ) is linearly
independent.