This document contains the slides for a presentation on functional programming (FP) and the Cats library in Scala. It begins with introductions and explains that the goal is to provide a practical guide to starting with FP and Cats. It then discusses some key FP concepts like immutable values, functions, and combining values using structures like Semigroup and Monoid. It demonstrates how Cats implements these concepts and provides type class instances for common types like List and Option using implicits. The presentation emphasizes how FP focuses on combining and transforming values in new ways.

1. Bestiary of FP
Tomasz Kogut - @almendar
2016.09.03
with Cats

2. About me:
• Software / Data Engineer at
• Develops AdTech Platform
• Research department
• Works on processing lots of data really fast
• Scala since ~2011

3. Warning!
• This presentation is intended to be practical guide how
to start with FP and cats
• May contain inaccurate information on purpose
• May contain simply wrong information because of my
mistake for which I sincerely apologize - I’m no expert
• Questions during presentation will be highly
appreciated

4. Why this talk? (1)
• FP is a different kind of beast
• Does not reassembles anything you know
• Reading blogs do not help, it makes it probably even
worse
• It’s frustrating

5. Why this talk? (2)
• There is much to learn
• Accepting this is the first step you have to make
• I’ve made some of the hops and I want to share so
you don’t have to go through some of the daunting
things

6. What FP is all about?
(1)
• Functions?
• Higher order functions?
• Immutability?
• Referential transparency?

7. What FP is all about?
(2)
• How stupid it may sound FP is about values
• Values are: bits, ints, data structures,
functions, types
• What FP does for us it allows us to
combine values and look at them as a new
value
• This is what we’ll be doing throughout the
presentation

8. Combining
values

9. Product
class Foo
class Bar
case class FooBarProduct(
foo: Foo,
bar: Bar
)
Tuples and cartesian product anyone?

10. Semigroup
Take two values and produce one

11. trait Semigroup[A] {
}

12. trait Semigroup[A] {
def combine(a1: A, a2: A): A
}

13. Group-like structures
Totalityα Associativity Identity Divisibility Commutativity
Semicategory Unneeded Required Unneeded Unneeded Unneeded
Category Unneeded Required Required Unneeded Unneeded
Groupoid Unneeded Required Required Required Unneeded
Magma Required Unneeded Unneeded Unneeded Unneeded
Quasigroup Required Unneeded Unneeded Required Unneeded
Loop Required Unneeded Required Required Unneeded
Semigroup Required Required Unneeded Unneeded Unneeded
Monoid Required Required Required Unneeded Unneeded
Group Required Required Required Required Unneeded
Abelian Group Required Required Required Required Required
https://en.wikipedia.org/wiki/Outline_of_algebraic_structures
Why “Semigroup” and not “ValuesCombiner”

14. object SuperAdder {
def add[A : Semigroup](a1: A, a2: A): A = Semigroup[A].combine(a1,a2)
}
case class ComplexNumber(x: Double,i: Double)
object ComplexNumber {
implicit val semiGroup = new Semigroup[ComplexNumber] {
def combine(a1: ComplexNumber, a2: ComplexNumber): ComplexNumber =
ComplexNumber(a1.x+a2.x, a1.i + a2.i)
}
}
SuperAdder.add(1,2) //res1: Int = 3
SuperAdder.add(ComplexNumber(1.2, 2.3), ComplexNumber(2.4, 3.4)) //res2: ComplexNum
SuperAdder.add("Hello ", "world") //res3: String = Hello world

15. What about Semigroup
for List, Option,
Future?

16. <console>:13: error: class Option takes type parameters
val optionSemigroup = new Semigroup[Option] {}
val optionSemigroup = new Semigroup[Option[Int]] {}
This would do the job but we can do better

17. Higher Kinded Types
• Option, List ect. are type constructors.
Like normal constructors but for types.
• They take a type as argument
• Some say that they have a “hole”
• Scala compiler knows about this

18. scala> :kind -v String
java.lang.String's kind is A
*
This is a proper type.
scala> :kind -v Either
scala.util.Either's kind is F[+A1,+A2]
* -(+)-> * -(+)-> *
This is a type constructor: a 1st-order-kinded type.
scala> :kind -v Option
scala.Option's kind is F[+A]
* -(+)-> *
This is a type constructor: a 1st-order-kinded type

19. Now the scary part
scala> :kind -v trait Foo[X[_]]
Foo's kind is X[F[A]]
(* -> *) -> *
This is a type constructor that takes type constructor(s): a higher-kin
at when you put inside a type that when put inside another type create

20. trait SemigroupK[F[_]] {
def combineK[A](fa1: F[A], fa2: F[A]): F[A]
}
implicit val optionSemigroupK = new SemigroupK[Option] {
def combineK[A](fa1: Option[A], fa2: Option[A]): Option[A] =
fa1 orElse fa2
}
implicit val listSemigroup = new SemigroupK[List] {
def combineK[A](fa1: List[A], fa2: List[A]): List[A] = fa1 ++ fa2
}
listSemigroup.combineK(List(1,2,3), List(4,5,6))
//res3: List[Int] = List(1, 2, 3, 4, 5, 6)
SemigroupK

21. • TypeK is a thing
• “K” stands for kind
• Our effect works on higher-kinder types
• SemigroupK, MonoidK, FunctionK

22. Semigroup(K) in Cats
• Both effects are provided by cats
• For std types there are ready instances
• The whole thing is to do the right imports

23. import cats._
import cats.implicits._
Semigroup[Int].combine(1,2)
//res0: Int = 3
SemigroupK[List].combineK(List(Some(1), Some(3)), List(Some(2)))
//res1: List[Some[Int]] = List(Some(1), Some(3), Some(2))

24. Semigroup[Int]
What is this?
object Semigroup extends SemigroupFunctions[Semigroup] {
@inline
final def apply[A](implicit ev: Semigroup[A]): Semigroup[A] = ev
}

25. Creating Effects
• This is very common in Cats
• TypeConstructor[X].someMethod
• Heavy use of implicits and packages
objects

26. • import cats._
make all types available in scope like
Semigroup, Monad, Applicative ect.
Like Predef for Scala.
• import cats.implicits._
puts ALL implicit into the scope using
package object trick

27. package object instances {
object all extends AllInstances
object either extends EitherInstances
object function extends FunctionInstances
object list extends ListInstances
object option extends OptionInstances
object set extends SetInstances
object stream extends StreamInstances
object vector extends VectorInstances
object map extends MapInstances
object future extends FutureInstances
object string extends StringInstances
object int extends IntInstances
object byte extends ByteInstances
object long extends LongInstances
object char extends CharInstances
object short extends ShortInstances
object float extends FloatInstances
object double extends DoubleInstances
object boolean extends BooleanInstances
object unit extends UnitInstances
object bigInt extends BigIntInstances
object bigDecimal extends BigDecimalInstances
object try_ extends TryInstances
object tuple extends TupleInstances
}
package object syntax {
object all extends AllSyntax
object applicative extends ApplicativeSyntax
object applicativeError extends ApplicativeErrorSyntax
object apply extends ApplySyntax
object bifunctor extends BifunctorSyntax
object bifoldable extends BifoldableSyntax
object bitraverse extends BitraverseSyntax
object cartesian extends CartesianSyntax
object coflatMap extends CoflatMapSyntax
object coproduct extends CoproductSyntax
object comonad extends ComonadSyntax
object compose extends ComposeSyntax
object contravariant extends ContravariantSyntax
object either extends EitherSyntax
object eq extends EqSyntax
object flatMap extends FlatMapSyntax
object foldable extends FoldableSyntax
object functor extends FunctorSyntax
object functorFilter extends FunctorFilterSyntax
object group extends GroupSyntax
object invariant extends InvariantSyntax
object list extends ListSyntax
object monadCombine extends MonadCombineSyntax
object monadFilter extends MonadFilterSyntax
object monoid extends MonoidSyntax
object option extends OptionSyntax
object order extends OrderSyntax
object partialOrder extends PartialOrderSyntax
object profunctor extends ProfunctorSyntax
object reducible extends ReducibleSyntax
object semigroup extends SemigroupSyntax
object semigroupk extends SemigroupKSyntax
object show extends Show.ToShowOps
object split extends SplitSyntax
object strong extends StrongSyntax
object transLift extends TransLiftSyntax
object traverse extends TraverseSyntax
object traverseFilter extends TraverseFilterSyntax
object tuple extends TupleSyntax
object validated extends ValidatedSyntax
object writer extends WriterSyntax
}
package cats
object implicits extends syntax.AllSyntax with instances.AllInstances

28. Instances
trait ListInstances extends cats.kernel.instances.ListInstances {
implicit val catsStdInstancesForList:
TraverseFilter[List]
with MonadCombine[List]
with Monad[List]
with CoflatMap[List]
with RecursiveTailRecM[List] =
new TraverseFilter[List]
with MonadCombine[List]
with Monad[List]
with CoflatMap[List]
with RecursiveTailRecM[List] {
def combineK[A](x: List[A], y: List[A]): List[A] = x ++ y
(...)
}

29. MonadCombine
Alternative
MonoidK
SemigroupK

30. Syntax
trait SemigroupSyntax {
implicit def catsSyntaxSemigroup[A: Semigroup](a: A):
SemigroupOps[A] = new SemigroupOps[A](a)
}
final class SemigroupOps[A: Semigroup](lhs: A) {
def |+|(rhs: A): A = macro Ops.binop[A, A]
def combine(rhs: A): A = macro Ops.binop[A, A]
}
List(1) |+| List(2, 2, 4)
We can do both:
List(1) combine List(2, 2, 4)

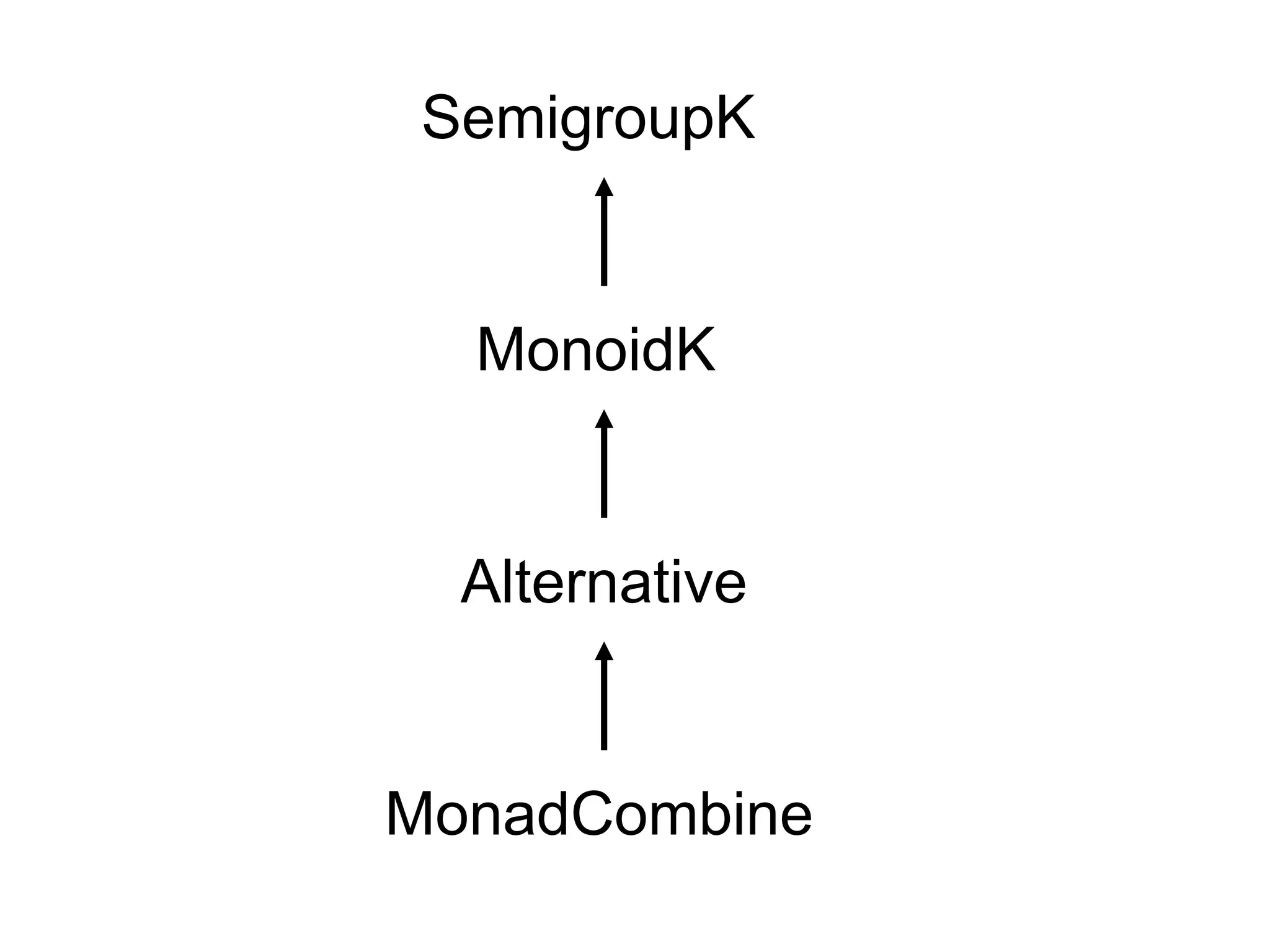
31. Monoid(K)
trait Monoid with Semigroup[A] {
def empty: A
}
@typeclass
trait MonoidK[F[_]] extends SemigroupK[F] { self =>
def empty[A]: F[A]
}
• @typeclass annotation comes from simulacrum
• It generates code
• “Jump to source” might not work in Cats src code

32. Monoid examples
• type: Int
combine: +
empty: 0
• type: Int
combine: *
empty: 1
• type: String
combine: +
empty: “”

33. Can we always create a monoid?
type NEL[A] = (A, List[A])
val nelMonoid = new MonoidK[NEL] {
def combineK[A](n1: NEL[A], n2: NEL[A]): NEL[A] =
(n1._1, (n1._2 :+ n2._1) ++ n2._2)
def empty[A]: NEL = ???
}

34. • One may end-up writing effect class for some data
structure that it is impossible
• http://stackoverflow.com/questions/32477292/fold-on-
nonemptylist/32479640#32479640
• It took me about 2 hours to realize this

35. trait Ord
case object GT extends Ord
case object LT extends Ord
case object EQ extends Ord
object Ord {
implicit object OrderingMonoid extends Monoid[Ord] {
def empty(): Ord = EQ
def combine(x:Ord, y: Ord): Ord = x match {
case EQ => y
case LT => LT
case GT => GT
}
}
}
Monoid example

36. def palindromeFirst(s1: String, s2: String): Ord
def shorterFirst(s1: String, s2: String): Ord
val res = List(palindromeFirst _, shorterFirst _).map{ f =>
f("ANNA", “BARBARA”)
}
Foldable[List].fold(res)(implicit OrderingMonoid)
// res0(: Ord = GT

37. Foldable
• Fold is surprisingly powerful
http://www.cs.nott.ac.uk/~pszgmh/fold.pdf
• Foldable has most of the collections api on it:
find, exists, forAll, filter, isEmpty,
• It allows to reduce collection to single element
• It can make use of Monoids

38. Foldable and monoid
example 2
def foldMap[A, B](fa: F[A])(f: A => B)(implicit B: Monoid[B]): B =
foldLeft(fa, B.empty)((b, a) => B.combine(b, f(a)))
val lineItems: List[LineItem] = ...
//explicit summoning Foldable
val totalInvoiceValue = Foldable[List].foldMap(lineItems){_.value}
//using syntax ops
val totalInvoiceValue = lineItems.foldMap { _.value }

39. Functors
trait Functor[F[_]] {
def map[A,B](fa:F[A])(f: A=>B): F[B]
}
Functor[List].map(List(1,2,3))(_ + 1)

40. Composing functors
val k = Functor[Try] compose Functor[List] compose Functor[Option]
k.map(Success(List(Some(22), Some(33), None)))(_+1)
//res19: scala.util.Try[List[Option[Int]]] = Success(List(Some(23), Some(34), None)))

41. Applicatives
The story of derived combinators
//we want map for this function
val addTwoInts = {(_:Int) + (_:Int)}
addTwoInts(2,3) //res0:Int = 5

42. trait Applicative[F[_]] {
def map2[A,B,C](fa:F[A], fb: F[B])(f: (A,B) => C): F[C]
def unit[A](a: => A): F[A]
}
Let’s get some stuff for free!!!
Applicatives

43. trait Applicative[F[_]] {
def map2[A,B,C](fa:F[A], fb: F[B])(f: (A,B) => C): F[C]
def unit[A](a: => A): F[A]
}

44. trait Applicative[F[_]] {
def map2[A,B,C](fa:F[A], fb: F[B])(f: (A,B) => C): F[C]
def unit[A](a: => A): F[A]
def map[A,B](fa:F[A])(f: A=>B): F[B] =
map2(fa, (): Unit))((a,_) => f(a))
}

45. trait Applicative[F[_]] {
def map2[A,B,C](fa:F[A], fb: F[B])(f: (A,B) => C): F[C]
def unit[A](a: => A): F[A]
def map[A,B](fa:F[A])(f: A=>B): F[B] =
map2(fa, (): Unit))((a,_) => f(a))
def product[A,B](fa: F[A], fb: F[B]): F[(A,B)] =
map2(fa,fb)((a,b) => (a,b))
}

46. trait Applicative[F[_]] {
def map2[A,B,C](fa:F[A], fb: F[B])(f: (A,B) => C): F[C]
def unit[A](a: => A): F[A]
def map[A,B](fa:F[A])(f: A=>B): F[B] =
map2(fa, (): Unit))((a,_) => f(a))
def product[A,B](fa: F[A], fb: F[B]): F[(A,B)] =
map2(fa,fb)((a,b) => (a,b))
def lift[A,B,C](x: A => B): F[A] => F[B] = { fa:F[A] =>
map(fa)(x)
} //pimp my API
}

47. trait Applicative[F[_]] {
def map2[A,B,C](fa:F[A], fb: F[B])(f: (A,B) => C): F[C]
def unit[A](a: => A): F[A]
def map[A,B](fa:F[A])(f: A=>B): F[B] =
apply(unit(f))(fa)
def product[A,B](fa: F[A], fb: F[B]): F[(A,B)] =
map2(fa,fb)((a,b) => (a,b))
def lift[A,B,C](x: A => B): F[A] => F[B] = { fa:F[A] =>
map(fa)(x) } //pimp my func
def traverse[A,B](as: List[A])(f: A => F[B]): F[List[B]] =
as.foldRight(unit(List[B]()))((a,fbs) => map2(f(a), fbs)
{ _ :: _ }
)
}

48. trait Applicative[F[_]] {
(…)
def unit[A](a: => A): F[A]
def map2[A,B,C](fa:F[A], fb: F[B])(f: (A,B) => C): F[C]
def map3[A,B,C,D](fa: F[A], fb: F[B], fc: F[C])
(f:(A,B,C) => D): F[D] =
map2(map2(map2(unit(f.curried), fa)(_(_)), fb)(_(_)), fc)(_(_))
}
def curried[A,B,C](f: (A,B) => C): A => B => C = { a => { b =>
f(a,b)
}}

49. trait Applicative[F[_]] {
(…)
def map3[A,B,C,D](fa: F[A], fb: F[B], fc: F[C])
(f:(A,B,C) => D): F[D] =
map2(map2(map2(unit(f.curried), fa)(_(_)), fb)(_(_)), fc)(_(_))
}

50. trait Applicative[F[_]] {
(…)
def map3[A,B,C,D](fa: F[A], fb: F[B], fc: F[C])
(f:(A,B,C) => D): F[D] =
map2(map2(map2(unit(f.curried), fa)(_(_)), fb)(_(_)), fc)(_(_))
def apply[A,B](fab: F[A=>B])(fa:F[A]): F[B] =
map2(fab,fa)(_(_))
}

51. trait Applicative[F[_]] {
(…)
def map3[A,B,C,D](fa: F[A], fb: F[B], fc: F[C])
(f:(A,B,C) => D): F[D] =
apply(apply(apply(unit(f.curried))(fa))(fb))(fc)
def apply[A,B](fab: F[A=>B])(fa:F[A]): F[B] =
map2(fab,fa)(_(_))
}

52. trait Applicative[F[_]] {
(…)
def map3[A,B,C,D](fa: F[A], fb: F[B], fc: F[C])
(f:(A,B,C) => D): F[D] =
apply(apply(apply(unit(f.curried))(fa))(fb))(fc)
def map4[A,B,C,D,E]
def map5[A,B,C,D,E,F]
def apply[A,B](fab: F[A=>B])(fa:F[A]): F[B] =
map2(fab,fa)(_(_))
}
mapN

53. Writting combinators
• It turn out that applicative can be expressed with
different set of operations
• map2 + unit
• apply + unit

54. def apply[A,B](fab: F[A=>B])(fa:F[A]): F[B] =
map2(fab,fa)(_(_))
def map2[A,B,C](fa: F[A], fb: F[B])(f: (A,B) => C): F[C] =
apply(apply(unit(f.curried))(fa))(fb)
map2 and apply

55. Usage of Applicative
case class Charts(
books: Seq[Book],
music: Seq[Album],
games: Seq[Game]
)
def topBooks: Future[Seq[Book]] = ???
def topMusic: Future[Seq[Album]] = ???
def topGames: Future[Seq[Album]] = ???
Applicative[Future].map3(topBooks, topMusic, topGames)(Charts(_,_,_))
Another use case is Validation

56. Cats Applicative helpers
import cats.implicits._
(topBooks |@| topMusic |@| topGames) map { Charts(_,_,_) }
Applicative builders using code generation
/* Very, very, very high level view on how this works */
class CartesianBuilderN {
def |@|(a: Applicative): CartesianBuilderN+1
def map(f: FunctionN): Applicative
}

57. Applicatives compose
val futOptAppl =
Applicative[Future] compose
Applicative[Option]
futOptAppl.map2(Future(Some(22)),Future(Some(33))) { _ + _ }
//res47: scala.concurrent.Future[Option[Int]] = Success(Some(55))

58. Monads
• You use them every day map/flatMap
• Monads are powerful abstraction
• They have most of the combinators
• At the same time not all data structures
can be expressed as Monads

59. class DBRepo[F[_]] {
def getUserLoging(id: Long)(implicit F: Monad[F]): F[String] =
F.pure(id.toString)
def getUserEmail(id: Long)(implicit F: Monad[F]): F[String] =
F.pure(id.toString)
def getUser(id: Long)(implicit F: Monad[F]) : F[User] = {
F.flatMap(getUserLoging(id)) { login =>
F.map(getUserEmail(id)) { email =>
User(login, email)
}
}
}
}
val repo1 = new DBRepo[Future]
val repo2 = new DBRepo[Task]

60. class DBRepo[F[_]] {
def getUserLoging(id: Long)(implicit F: Monad[F]): F[String] =
F.pure(id.toString)
def getUserEmail(id: Long)(implicit F: Monad[F]): F[String] =
F.pure(id.toString)
def getUser(id: Long)(implicit F: Monad[F]) : F[User] =
for {
login <- getUserLoging(id)
email <- getUserEmail(id)
} yield User(login, email)
}
val repo1 = new DBRepo[Future]
val repo2 = new DBRepo[Task]

61. Monads
for {
i <- List(Option(1), Option(2))
j <- List(Option(3), Option(4))
} yield i + j
Monads don’t compose (usually), so the two below won’t wor
Monad[List] compose Monad[Option]

62. Monads
this will, but it’s ugly
val p = for {
i <- List(Option(1), Option(2))
j <- List(Option(3), Option(4))
} yield {
for {
k <- i
l <- j
} yield k+l
}

63. Monad transformers
val k = for {
i <- OptionT(List[Option[Int]](Option(1), Option(2)))
j <- OptionT(List[Option[Int]](Option(3), Option(4)))
} yield i + j
…this will also and it’s nice:

64. Monad transformers
• Cats have multiple instances of those
• EitherT, IdT, OptionT, StateT, WriterT
• TypeT[F[_], A] wraps F[Type[A]]
• E.g. OptionT[List, Int] wraps List[Option[Int]]

65. Effectful functions
• A => F[B]
• Returned value in some kind of
effect/context
• More common than one might think

66. // Id => Future[Long]
def getCustomerById(long: Id): Future[Customer]
// CharSequence => Option[String]
def findFirstIn(source: CharSequence): Option[String]
//Int => List[Int]
def listFromZeroToN(n: Int): List[Int]
we want to combine those

67. Kleisli
final case class Kleisli[F[_], A, B](run: A => F[B])
• It has all the good’ol combinators: flatMap, map, compose, apply ect.
• Used for composing effectful functions
• What kind of combinator can you use depends on what F is
• If you can have implicit effect for F you can call certain methods
def map[C](f: B => C)
(implicit F: Functor[F]): Kleisli[F, A, C] =
Kleisli(a => F.map(run(a))(f))
def flatMap[C](f: B => Kleisli[F, A, C])
(implicit F: FlatMap[F]): Kleisli[F, A, C] =
Kleisli((r: A) => F.flatMap[B, C](run(r))((b: B) => f(b).run(r)))

68. Kleisli
(A => B) andThen (B => C) => (A => C)
(A => F[B]) andThen (B => F[C]) => won't work
Kleisli(A => F[B]) andThen Kleisli(B => F[C]) => Kleisli(A => F[C])

69. There is more…
• Xor
• State
• Validated
• FreeMonads and FreeApplicatives
• Show
• Traverse

70. Simple RPC
• Let’s build a quick RPC API with
focus on HTTP
• We’ll take building blocks from what
we’ve seen

71. package object http {
type Service[A,B] = Kleisli[Future, A, B]
}

72. package object http {
type Service[A,B] = Kleisli[Future, A, B]
type HttpService = Service[Request, Response]
}

73. package object http {
type Service[A,B] = Kleisli[Future, A, B]
type HttpService = Service[Request, Response]
//Future[Either[A, B]]
type DecodeResult[T] =
EitherT[Future, DecodeFailure, T]
}

74. object Service {
def lift[A,B](f: A => Future[B]): Service[A,B] = Kleisli(f)
}
object HttpService {
def apply(f: PartialFunction[Request, Response]):
HttpService = Service.lift(liftToAsync(f))
def liftToAsync[A,B](f: A => B): A => Future[B] =
(a: A) => Future(f(a))
}

75. val httpService = HttpService {
case r1 @ Request(Get, "/") => Response(Ok)
case r2 @ Request(Post, "/") = Response(NotFound)
}
Http.runService(httpService)
Server

76. Client
We can reuse the HttpService type
val httpClient: HttpService = ???
val jsonResponseFromPipeline = httpService.map(_.body[Json])
val jsonFut: Future[DecodeResul[Json]] =
jsonResponseFromPipeline(Request(Get,"/"))

77. class AHClientWrapper(realClient: AHClient)
extends Request => Future[Response] {
def apply(req: Request): Future[Response] = {
//call realClient and return response
}
}
val httpClient: HttpService =
Kleisli(new AHClientWrapper(new AHClient))
Client

78. httpService.map(_.body[Json]) // Kleisli[Future, Request, Json]
//implementation
case class Response(code: HttpCode) extends Message {
def body[A](implicit decoder: EntityDecoder[A]):
DecodeResult[A] =
decoder.decode(this)
}
Decoding

79. trait EntityDecoder[T] { self =>
def decode(msg: Message): DecodeResult[T]
def map[T2](f: T => T2): EntityDecoder[T2] =
new EntityDecoder[T2] {
override def decode(msg: Message): DecodeResult[T2]
= self.decode(msg).map(f)
}
}
type DecodeResult[T] =
EitherT[Future, DecodeFailure, T]
This map is interesting

80. object EntitiyDecoder {
implicit def stringInstance = new EntityDecoder[String] {
def decode(msg: Message): DecodeResult[String] =
EitherT.pure[Future, DecodeFailure, String]("SomeString")
}
implicit def jsonInstance: EntityDecoder[Json] =
stringInstance.map(_.toJson)
}
trait Json
object Json {
implicit def fromString(s: String): JsonOps = JsonOps(s)
case class JsonOps(s: String) {
def toJson = new Json {}
}
}

81. Takeaways
• This stuff is hard
• You must want to learn it
• There is no other way as building your knowledge from the ground up
• Approach it without being biased - this is just a tool
• It will help you understand/read/write high-level scala code
• Not everyone will appreciate that style of coding and that’s fine.

82. Thank you