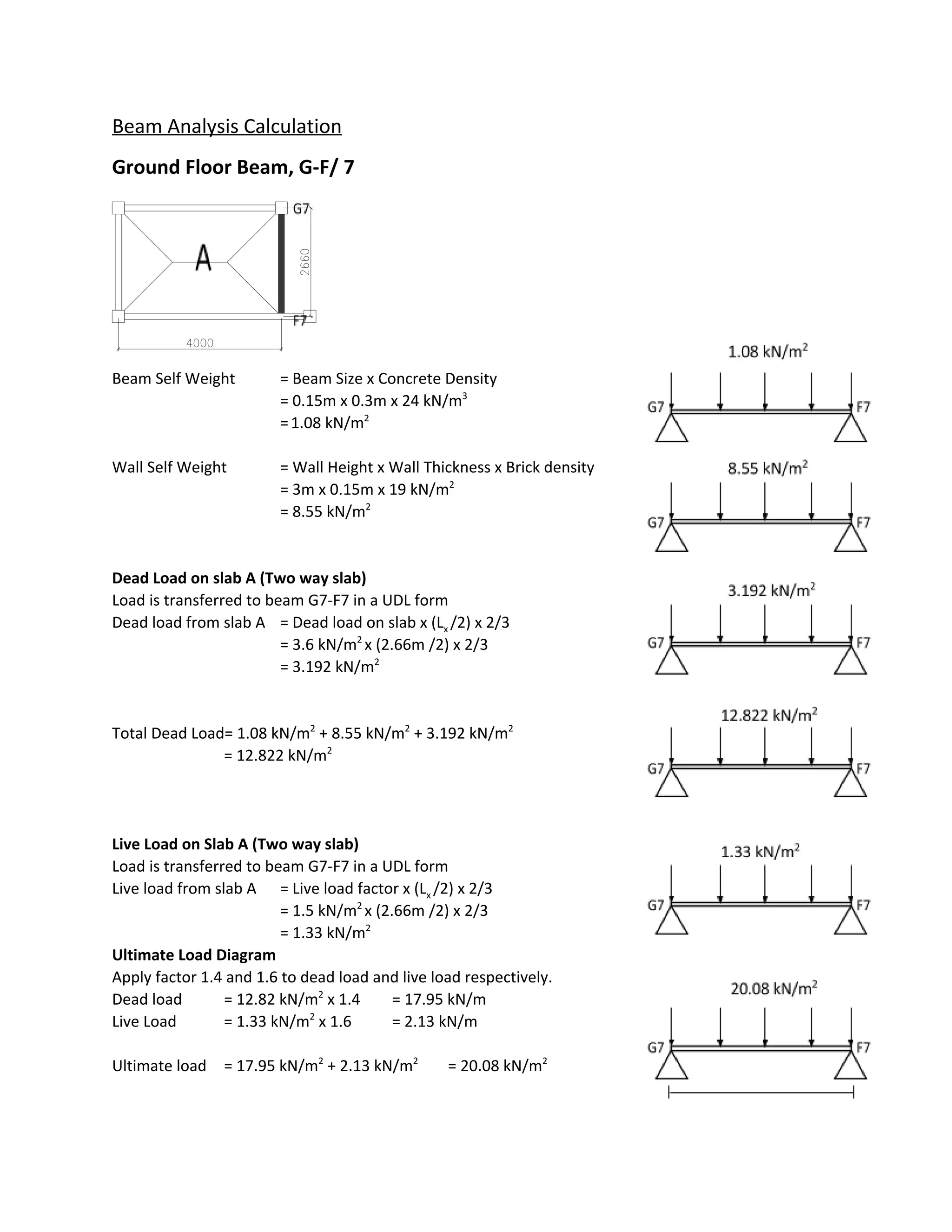
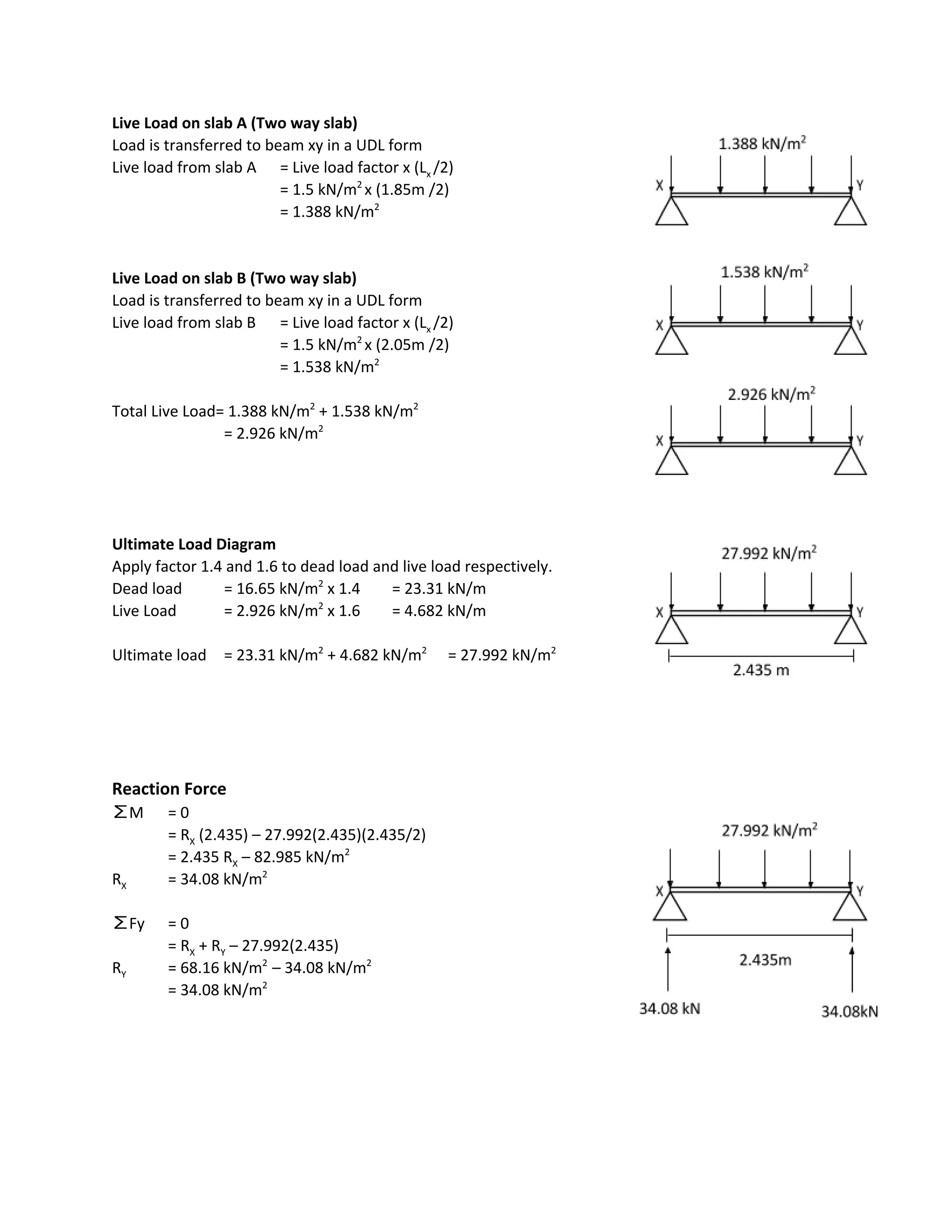
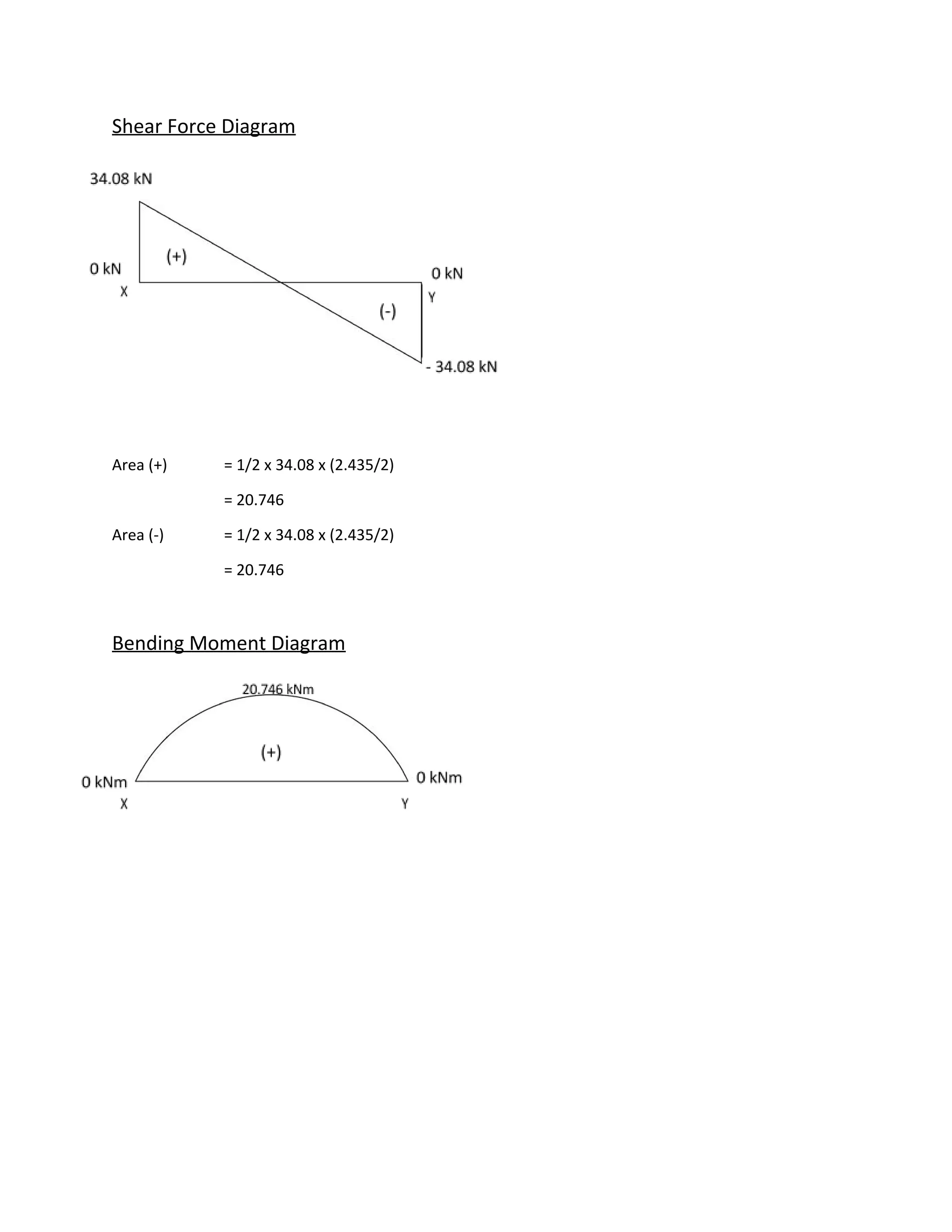
The document contains calculations for the beam analysis of several ground floor, first floor, and intermediate beams. It includes calculations for the beam and wall self-weights, slab dead and live loads transferred to each beam, total loads, load factors, reactions forces, shear force and bending moment diagrams. Load values and beam sizes are used to calculate beam self-weights, wall loads, slab loads, total loads, load factors, reaction forces at beam ends, and shear and bending moment values along each beam.