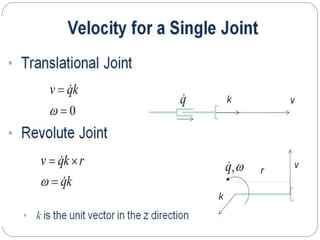
The document discusses differential kinematics involving skew symmetric matrices in complex cases where the axis of rotation is not fixed, leading to angular velocities from multiple distinct rotations. It defines skew symmetric matrices and explains their properties, along with the time-varying nature of rotation matrices and their derivatives. The content is centered on the mathematical representation and implications of rotation dynamics.

1. Differential Kinematics

6. Skew Symmetric Matrices
Complex Case:
When axis of rotation are not
fixed
Angular velocity is the result of
multiple rotations about distinct
axis.
For general representation of
angular velocities Skew
symmetric Matrices were

8. Definition
Skew matrix is a square matrix A whose
transpose is also its negative; that is, it satisfies
the condition -A = AT.
If the entry in the ith row and jth column is aij,i.e.
A = (aij)
then the skew symmetric condition is aij = −aji.
For example, the following matrix is skew-
symmetric:

10. Properties

12. Derivative of rotation matrix
Differentiating both
sides
1

13. Which shows that S is a skew symmetric
Now as
Multiplying both sides of equation-01
by R we get

16. Angular Velocity and Acceleration
Kinematics
 Suppose that rotation Matrix R is time varying
i.e.R=R(t)
 Time derivative of R is(as proved above)

18. Thanks