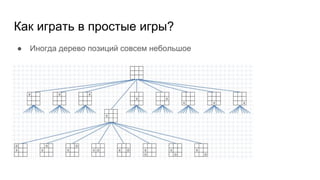
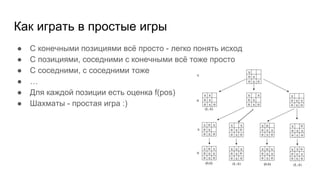
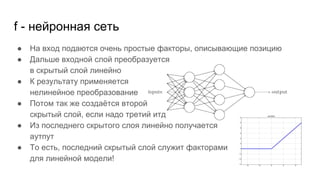
Автор делится своим опытом игры в нарды и описывает методы оценки игровых позиций с использованием вероятностей. Брошюра также затрагивает использование линейных функций и нейронных сетей для улучшения стратегии игры. В заключение, планируется создать визуализацию игры и провести турнир.

1. Учимся играть в нарды

2. О себе
● окончил мехмат МГУ
● 4 года в Гугле, занимался качеством поиска
● сейчас в Яндексе, занимаюсь качеством поиска
● 2 место на финале ACM ICPC 2010
● КМС по самбо
● 1 место на финале спортивного лагеря по нардам

3. О нардах (трик-трак, бэкгэммон, шеш-беш)
● Игре 5000 лет
● Игру придумали персы, чтобы унизить индусов
● Надо кидать 2 игральных кубика
● И выбирать хороший ход
● Крутых игроков кубики слушаются
● Жулики стачивают кубики

4. Как играть в простые игры?
● Иногда дерево позиций совсем небольшое

5. Как играть в простые игры
● С конечными позициями всё просто - легко понять исход
● С позициями, соседними с конечными всё тоже просто
● С соседними, с соседними тоже
● …
● Для каждой позиции есть оценка f(pos)
● Шахматы - простая игра :)

6. Как играть в игры посложнее
● Нарды - игра посложнее, так как набор ходов зависит от случая
● Даже если двое не меняют стратегию, результат может меняться
● Цель - максимизировать вероятность выирыша
● В остальном суть та же, только f(pos) - вероятность выигрыша
● Смотрим какие возможны ходы и выбираем позицию с лучшей оценкой
● Всё это хорошо, но позиций многовато!

7. Как обойтись без перебора
Люди как-то обходятся без перебора:
● 6 фишек подряд - это круто. Если у соперника, то плохо
● Если завёл в дом все фишки, а соперник ни одной, то это очень хорошо
● …
Можно попробовать делать то же самое:
● Создаём сотню таких характеристик позиций x1, …, x100
● Пытаемся оценивать позицию как f(x1, …, x100)
● Всё это хорошо, но откуда взять f?

8. Time-difference learning
Для начала поймём, как, уже имея какую-то f, оценить её качество:
● Пусть есть позиция pos1, f(pos1) = 0.9 (выигрываем с хорошей
вероятностью)
● Бросаем кубики, выбираем лучшую для нас позицию pos2
● Соперник бросает кубики, выбирает лучшую для него позицию pos3
● Допустим f(pos3) = 0.3 (с хорошей вероятностью проигрываем)
● Что-то явно пошло не так!
● На самом деле хотим, чтобы f(pos1) было примерно равно f(pos3)

9. Откуда брать такие пары позиций
● Если есть стратегия f, то мы можем заставить её играть саму с собой
● Одна партия - это набор позиций pos1, pos2, pos3, …, posK
● Мы хотим, чтобы f(pos1) ~= f(pos3) ~= f(pos5) …; f(pos2) ~= f(pos4) …
● То есть, (f(pos1) - f(pos3)) ^ 2 + (f(pos2) - f(pos4)) ^ 2 + … -> min
● После чего мы можем улучшить f и повторить этот процесс много раз

10. Линейная функция f
Самое простое решение - линейная f:
● f(x1, …, x100) = a1 * x1 + … + a100 * x100
● a1, …, a100 - параметры, которые надо подобрать, заставляя f играть
против себя
● (f(pos1) - f(pos3)) ^ 2 + (f(pos2) - f(pos4)) ^ 2 + … в этом случае -
квадратичная функция от a1, …, a100 - легко оптимизировать
● При хорошем выборе факторов будет уже играть не хуже людей
Проблемы построения факторов:
● Надо хорошо понимать игру
● Надо тратить усилия, чтобы их придумывать и описывать

11. f - нейронная сеть
● На вход подаются очень простые факторы, описывающие позицию
● Дальше входной слой преобразуется
в скрытый слой линейно
● К результату применяется
нелинейное преобразование
● Потом так же создаётся второй
скрытый слой, если надо третий итд
● Из последнего скрытого слоя линейно получается
аутпут
● То есть, последний скрытый слой служит факторами
для линейной модели!

12. План
● Описываем правила игры в коде
● Хорошенько тестируем
● Пишем несколько тупых базовых стратегий
● Уверенно выигрываем у них с помощью линейной f
● Уверенно выигрываем у неё с помощью нейросетевой f
● Визуализируем игру, чтобы можно было играть против людей
● Турнир по нардам на спецприз от ментора

13. Контакты
Алексей Гусаков
agusakov@gmail.com
vk.com/agusakov
+7 906 758 92 49