AtCoder ABC167D問題をコンテスト中は愚直に解いたので解説動画で述べられていた内容を自分なりにスライド化。 公式の動画解説の方が分かりやすいです。自分の理解のためにスライドにしました。 ダブリングの分かりやすい説明 (satanicさん) https://www.slideshare.net/satanic2/ss-72500089 この問題を文章で分かりやすく説明したもの(hamayanhamayanさん) https://www.hamayanhamayan.com/entry/2020/05/10/232914

1. AtCoder167Dを
ダブリングで解く
※公式の動画解説の方が分かりやすいです。自分の理解のためにスライドにしました。
ダブリングの分かりやすい説明 (satanicさん)
https://www.slideshare.net/satanic2/ss-72500089
この問題を文章で分かりやすく説明したもの(hamayanhamayanさん)
https://www.hamayanhamayan.com/entry/2020/05/10/232914
@recuraki

2. 問題概要(0indexにした例2の例)
• N個の町があり最初0にいる。それぞれ次の瞬間には町aiにワープする。K回ワープした場合の町の位置を求めよ。
• 必ず「ループ」ができる。例えば、入出力例2は、下の図のように3回目から3回ごとにループ(同じ町のワープを繰り返す)
• kが小さければ(例えば<=10*6)シミュレーションでも良いが、今回はk<=10*18なので到底間に合わない
アイデア1: 何回目のループの何個目かを計算することで解決するのがシンプルな解
⇒ただし、どこでループが起きているかなど書くと少し複雑になる
アイデア2: ダブリング(次のスライド以降で説明)
5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
1回目
2回目
3回目
4回目
5回目
6回目
7回目
8回目
ループ1
ループ2

3. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0
1
2
…
テーブル
まず、上のようなテーブルを考えます。

4. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先)
1
2
…
テーブル
まず、i=0のとき、「1回先はどの町にいるか」を書いていきます。
これは単に上のグラフをなぞればよいです。

5. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5
1
2
…
テーブル
まず、i=0のとき、「次はどの町にいるか」を書いていきます。
これは単に上のグラフをなぞればよいです。
0にいれば次は5

6. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4
1
2
…
テーブル
まず、i=0のとき、「次はどの町にいるか」を書いていきます。
これは単に上のグラフをなぞればよいです。
1にいれば次は4

7. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1
1
2
…
テーブル
まず、i=0のとき、「次はどの町にいるか」を書いていきます。
これは単に上のグラフをなぞればよいです。
2にいれば次は1

8. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4
1
2
…
テーブル
まず、i=0のとき、「次はどの町にいるか」を書いていきます。
これは単に上のグラフをなぞればよいです。
3にいれば次は4
※今回の題意では1からスタートし、町3にたどり着くことはないのですが、気にせずに代入します

9. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2
1
2
…
テーブル
まず、i=0のとき、「次はどの町にいるか」を書いていきます。
これは単に上のグラフをなぞればよいです。
4にいれば次は2

10. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1
2
…
テーブル
まず、i=0のとき、「次はどの町にいるか」を書いていきます。
これは単に上のグラフをなぞればよいです。
5にいれば次は1

11. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先)
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。

12. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先)
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
今0にいるときの2つ先を調べます（赤丸を調べたい）

13. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先)
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
今0にいるときの2つ先を調べます（赤丸を調べたい）
この時、一つ上のセルに注目します。これは、今、0にいるときの1つ先を示しています。

14. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先)
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
今0にいるときの2つ先を調べます（赤丸を調べたい）
この時、一つ上のセルに注目します。これは、今、0にいるときの1つ先を示しています。
ここでは、5を指しているので5の列の、参照したセルと同じ列にあるセルを確認します。

15. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
今0にいるときの2つ先を調べます（赤丸を調べたい）
この時、一つ上のセルに注目します。これは、今、0にいるときの1つ先を示しています。
ここでは、5を指しているので5の列の、参照したセルと同じ列にあるセルを確認します。
これにより「0の1つ先は5」「5の1つ先は1」なのですから、0の2つ先は1であると分かります。

16. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
同じように、1の2つ先はどこでしょうか？

17. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
同じように、1の2つ先はどこでしょうか？
先ほどと同様、一つ上のセルは4です。この4の一つ先は2だと分かります。
これにより「1の1つ先は4」「4の1つ先は2」なのですから、1の2つ先は2であると分かります

18. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
２の時は「2の1つ先は1」「1の1つ先は4」なので2の2つ先は4であると分かります

19. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
3の時は「3の1つ先は4」「4の1つ先は2」なので3の2つ先は2であると分かります
※実際3に遷移することはありませんが、気にせずに計算してください

20. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
4の時は「4の1つ先は2」「2の1つ先は1」なので4の2つ先は1であると分かります

21. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2
…
テーブル
次に、i=1のとき「2つ先にどこにいるか」を調べます。
5の時は「5の1つ先は1」「1の1つ先は4」なので5の2つ先は4であると分かります

22. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先)
…
テーブル
ここで、i=2の時を「4個先はどこにいるか」だとします。
0の4個先を求めます。先ほどと同様、一つ上のセルを見ます。
このセル(i=1の行)の意味を思い出すと2個先の位置を示すので、0の2個先は1だということがわかります。

23. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2
…
テーブル
ここで、i=2の時を「4個先はどこにいるか」だとします。
0の4個先を求めます。先ほどと同様、一つ上のセルを見ます。
このセル(i=1の行)の意味を思い出すと2個先の位置を示すので、0の2個先は1だということがわかります。
このまま、先ほどと同じ行(i=1の行)のセルを確認します。1の2個先は2だということが分かります。
つまり、「0の2つ先は1」「1の2つ先は2」なので0の4つ先は2であると分かります。

24. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4
…
テーブル
ここで、i=2の時を「4個先はどこにいるか」だとします。
同様に計算していきます。

25. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1
…
テーブル
ここで、i=2の時を「4個先はどこにいるか」だとします。
同様に計算していきます。

26. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4
…
テーブル
ここで、i=2の時を「4個先はどこにいるか」だとします。
同様に計算していきます。

27. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2
…
テーブル
ここで、i=2の時を「4個先はどこにいるか」だとします。
同様に計算していきます。

28. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
…
テーブル
ここで、i=2の時を「4個先はどこにいるか」だとします。
同様に計算していきます。

29. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
…
テーブル
できました。これで各町にいるとき、{1,2,4}個目がどの町にいるのかがわかります。

30. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
…
テーブル
それではここで、0の6個先のセルを求めてみましょう。

31. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
…
テーブル
それではここで、0の6個先のセルを求めてみましょう。
「0の2個先をX」だとしたら「Xの4個先がY」で、Yが求めたい「0の6個先」だと分かります。

32. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
…
テーブル
それではここで、0の6個先のセルを求めてみましょう。
「0の2個先をX」だとしたら「Xの4個先がY」で、Yが求めたい「0の6個先」だと分かります。
「0の2個先は1」です。

33. 5 4 1 4 2 1
町0 町1 町2 町3 町4 町5
i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
…
テーブル
それではここで、0の6個先のセルを求めてみましょう。
「0の2個先をX」だとしたら「Xの4個先がY」で、Yが求めたい「0の6個先」だと分かります。
「0の2個先は1」です。ここで1に注目すると1の4個先は4です。
つまり、0の6個先は4だと分かりました。

34. i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
3(8個先) 1 2 4 2 1 4
4(16個先) 2 4 1 4 2 1
5(32個先) 1 2 4 2 1 4
6(64個先) 2 4 1 4 2 1
7(128個先) 1 2 4 2 1 4
8(256個先) 2 4 1 4 2 1
上の表は先ほどと同じ入力で、i=8まで求めたものです。
これを利用して、kが大きな値の時を求めてみましょう。

35. i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
3(8個先) 1 2 4 2 1 4
4(16個先) 2 4 1 4 2 1
5(32個先) 1 2 4 2 1 4
6(64個先) 2 4 1 4 2 1
7(128個先) 1 2 4 2 1 4
8(256個先) 2 4 1 4 2 1
例えば、300個目を計算してみます。300 = 4 + 8 + 32 + 256なので、0の300個先を計算するには….

36. i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
3(8個先) 1 2 4 2 1 4
4(16個先) 2 4 1 4 2 1
5(32個先) 1 2 4 2 1 4
6(64個先) 2 4 1 4 2 1
7(128個先) 1 2 4 2 1 4
8(256個先) 2 4 1 4 2 1
例えば、300個目を計算してみます。300 = 4 + 8 + 32 + 256なので、0の300個先を計算するには….
「0の4つ先は2」

37. i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
3(8個先) 1 2 4 2 1 4
4(16個先) 2 4 1 4 2 1
5(32個先) 1 2 4 2 1 4
6(64個先) 2 4 1 4 2 1
7(128個先) 1 2 4 2 1 4
8(256個先) 2 4 1 4 2 1
例えば、300個目を計算してみます。300 = 4 + 8 + 32 + 256なので、0の300個先を計算するには….
「0の4つ先は2」「2の8つ先は4」「4の32つ先は1」「1の256つ先は4」
ということで0の300個先は4ということが分かりました。

38. i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
3(8個先) 1 2 4 2 1 4
4(16個先) 2 4 1 4 2 1
5(32個先) 1 2 4 2 1 4
6(64個先) 2 4 1 4 2 1
7(128個先) 1 2 4 2 1 4
8(256個先) 2 4 1 4 2 1
例えば、300個目を計算してみます。300 = 4 + 8 + 32 + 256なので、0の300個先を計算するには….
「0の4つ先は2」「2の8つ先は4」「4の32つ先は1」「1の256つ先は4」
ということで0の300個先は4ということが分かりました。
X個先の数字を見て分かる通り、Xは2の累乗です。今回の300 = 0b100101100でしたら、LSBから3,4,6,9bit目が立って
いるので、今いる位置0からスタートしてi=2,3,5,8の順に今いる位置を更新していけばよいです。

39. i
今いる場所
0 1 2 3 4 5
0(1個先) 5 4 1 4 2 1
1(2個先) 1 2 4 2 1 4
2(4個先) 2 4 1 4 2 1
3(8個先) 1 2 4 2 1 4
4(16個先) 2 4 1 4 2 1
5(32個先) 1 2 4 2 1 4
6(64個先) 2 4 1 4 2 1
7(128個先) 1 2 4 2 1 4
8(256個先) 2 4 1 4 2 1
X個先の数字を見て分かる通り、Xは2の累乗です。今回の300 = 0b100101100でしたら、LSBから3,4,6,9bit目が立って
いるので、今いる位置0からスタートしてi=2,3,5,8の順に今いる位置を更新していけばよいです。
尚、「の順に」と書きましたが、実際は順不同です。例えば、上記は5,8,3,2の順でたどっていますが結果は変わりませ
ん。

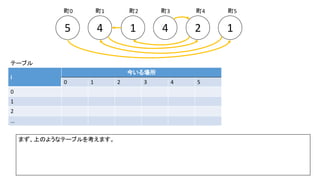
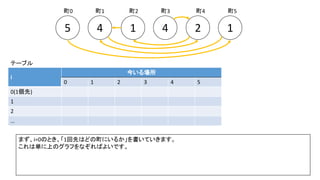
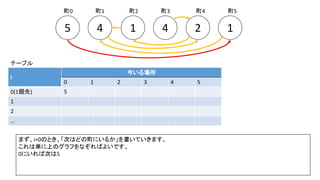
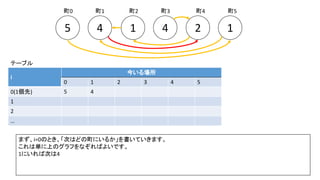
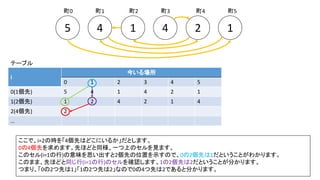
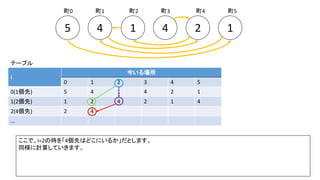
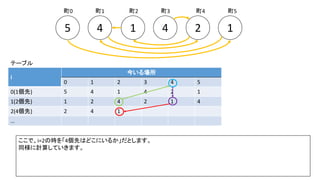
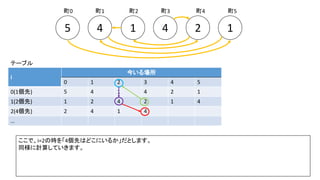
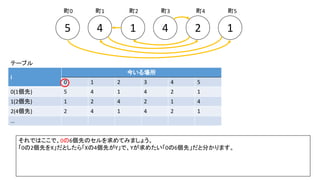
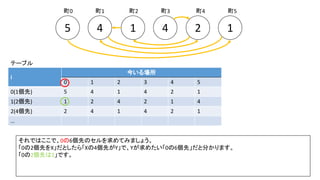
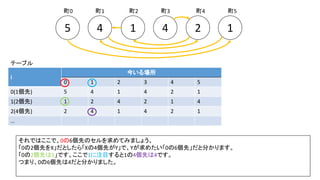
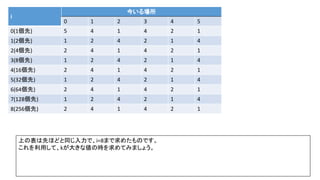
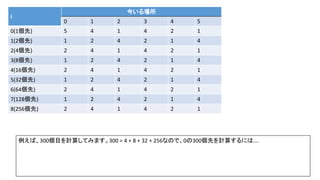
40. Debug printfを入れた前ページのサンプルでn=300の時の例(inputは1indexedで、そのあとの出力は0indexedです)
./a.out
6 300
6 5 2 5 3 2
i[0]: 5 4 1 4 2 1
i[1]: 1 2 4 2 1 4
i[2]: 2 4 1 4 2 1
i[3]: 1 2 4 2 1 4
i[4]: 2 4 1 4 2 1
i[5]: 1 2 4 2 1 4
i[6]: 2 4 1 4 2 1
i[7]: 1 2 4 2 1 4
i[8]: 2 4 1 4 2 1
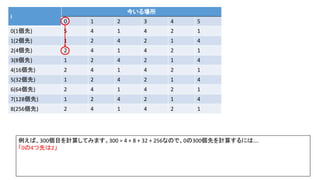
k=000000000000000000000000000000000000000000000000000100101100 (300を2進数60桁にしたもの)
final:
j[0]: K 300 j 0K>>j 0
j[1]: K 300 j 1K>>j 0
j[2]: K 300 j 2K>>j 1
> hit! > after: 0 -> after2
j[3]: K 300 j 3K>>j 1
> hit! > after: 2 -> after4
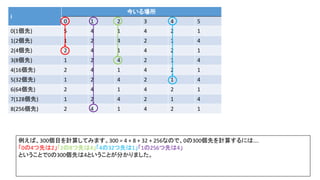
j[4]: K 300 j 4K>>j 0
j[5]: K 300 j 5K>>j 1
> hit! > after: 4 -> after1
j[6]: K 300 j 6K>>j 0
j[7]: K 300 j 7K>>j 0
j[8]: K 300 j 8K>>j 1
> hit! > after: 1 -> after4
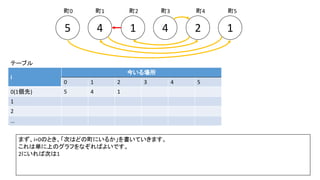
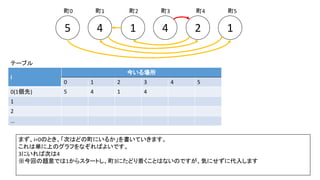
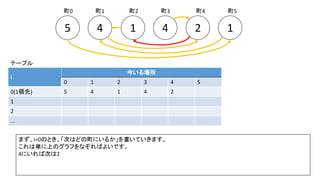
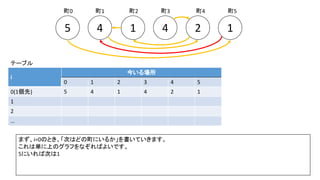
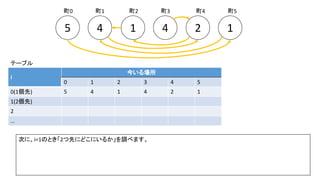
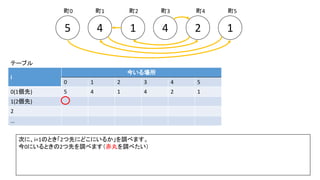
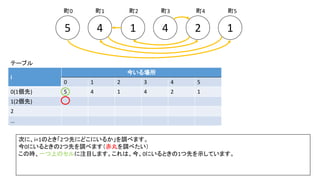
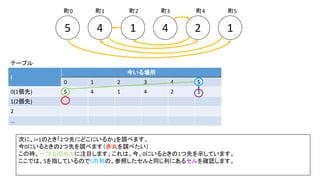
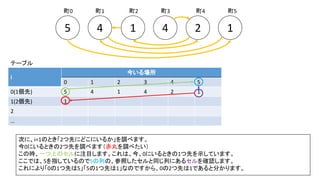
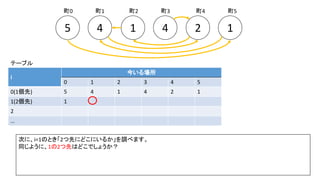
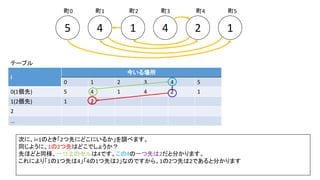
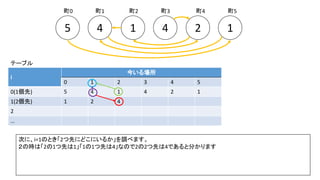
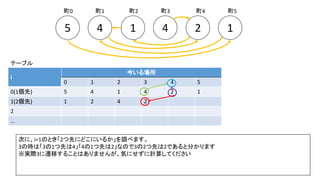
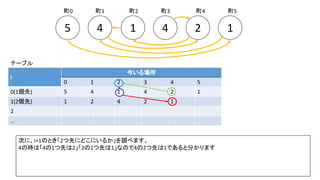
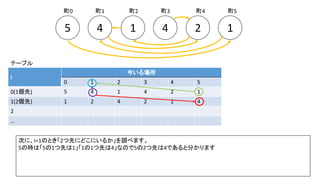
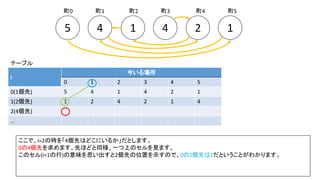
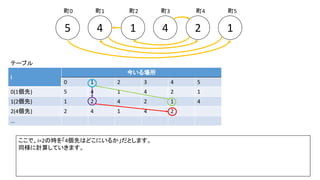
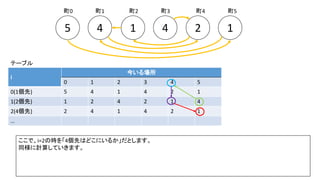
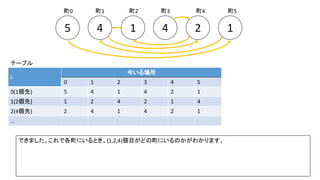
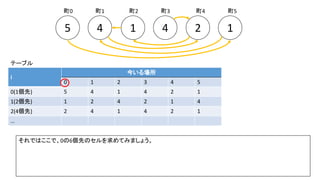
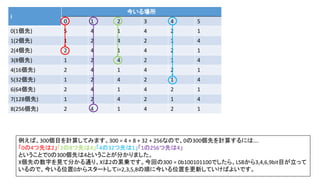
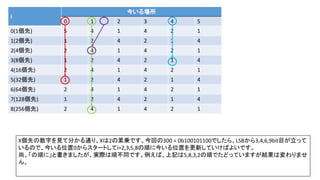
前スライドの表はi=8までの表を作りました。実際のコンテストでは入力が10^18以下、ということで、i=60程度の表を事前計
算した実装が多かったようです。log10(2^60) = 18.06のため