Download to read offline
Uploaded byAdam Getchell
April 2015 APS presentation
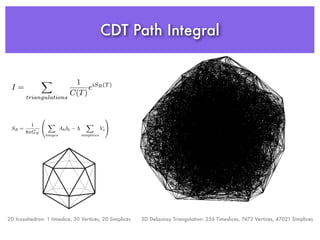
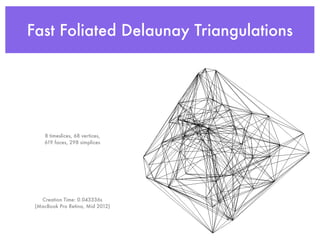
The document discusses the Newtonian limit in causal dynamical triangulation (CDT) and its compatibility with general relativity at cosmological scales. It explores computational methods for calculating distances and re-implementing CDT using modern C++ and various libraries, emphasizing efficiency and ease of contribution. The author invites interested individuals to join in the work.
More Related Content
![Polymer [ बहुलक ] Chemistry Notes PDF - Irfanullah Mehar - JJ Sir Chemistry.pdf](https://cdn.slidesharecdn.com/ss_thumbnails/polymerchemistrynotespdf-irfanullahmehar-jjsirchemistry-260210172118-3f9b37f7-thumbnail.jpg?width=640&height=640&fit=bounds)
April 2015 APS presentation
- 1. The Newtonian Limitin CDT Adam Getchell (UC Davis) acgetchell@ucdavis.edu
- 2. Path Integral Credit: NASA/WMAPScience Team
- 3. CDT Path Integral 3DDelaunay Triangulation: 256 Timeslices, 7473 Vertices, 47021 Simplices2D Icosahedron: 1 timeslice, 30 Vertices, 20 Simplices
- 4. Does CDT havea Newtonian Limit? • CDT looks like GR at cosmological scales, does it have a Newtonian limit? • At first glance, this is hard: • CDT is not well suited for approximating smooth classical space-times • We don’t have the time or resolution to watch objects fall F = Gm1m2 r2
- 5. A trick fromGR • The static axisymmetric Weyl metric • With two-body solutions • Leads to a “strut” • With a stress • That can be integrated to get the Newtonian force ds2 = e2 dt2 e2(⌫ ) dr2 + dz2 r2 e 2 d 2 (r, z) = µ1 R1 µ2 R2 , Ri = q r2 + (z zi) 2 Tzz = 1 8⇡G ⇣ 1 e ⌫(r,z) ⌘ 2⇡ (r) F = Z TzzdA = 1 4G ⇣ 1 e ⌫(r,z) ⌘ = Gm1m2 (z1 z2) 2 for µi = Gmi ⌫(0, z) = 4µ1µ2 (z1 z2) 2 ⌫(r, z) = µ2 1r2 R4 1 µ2 2r2 R4 2 + 4µ1µ2 (z1 z2) 2 r2 + (z z1) (z z2) R1R2 1
- 6. Measurements in CDT Mass➔ Epp quasilocal energy • In 2+1 CDT, extrinsic curvature at an edge is proportional to the number of connected tetrahedra • In 3+1 CDT, extrinsic curvature at a face is proportional to the number of connected pentachorons (4-simplices) Einstein Tensor in Regge Calculus (Barrett, 1986) EE ⌘ 1 8⇡G Z ⌦ d2 x p | | ⇣p k2 l2 p ¯k2 ¯l2 ⌘ l ⌘ µ⌫ lµ⌫ k ⌘ µ⌫ kµ⌫
- 7. Some Computational Methods Distance •Calculate single-source shortest path between the two masses using Bellman-Ford algorithm in O(VE) • Modify allowed moves in a sweep to not permit successive moves which increase or decrease distance Hausdorff Distance • Calculate Voronoi diagram of Delaunay triangulation • Use Voronoi diagram to find minimum Hausdorff distance for sets (Huttenlocher,︎︎︎︎ Kedem︎︎︎︎︎ and Kleinberg) in O((m+n) 6 log(mn))︎︎︎
- 8. My Work Re-implement CDT •Rewrite in modern C++ • C++14 standard • Use well-known libraries • CGAL • GeomView • Eigen • MPFR, GMP • Intel TBB
- 9. My Work Use currenttoolchains • LLVM/Clang • Hosted on GitHub • Travis-CI for continuous testing • GoogleMock • CMake for cross-platform building • Doxygen for document generation • Others Easy to evaluate, use, and contribute
- 10. Fast Foliated DelaunayTriangulations 8 timeslices, 68 vertices, 619 faces, 298 simplices Creation Time: 0.043336s (MacBook Pro Retina, Mid 2012)
- 11. Fast Foliated DelaunayTriangulations 256 timeslices, 222,136 vertices, 2,873,253 faces, 1,436,257 simplices Creation Time: 284.596s (MacBook Pro Retina, Mid 2012)
- 12.
- 13.