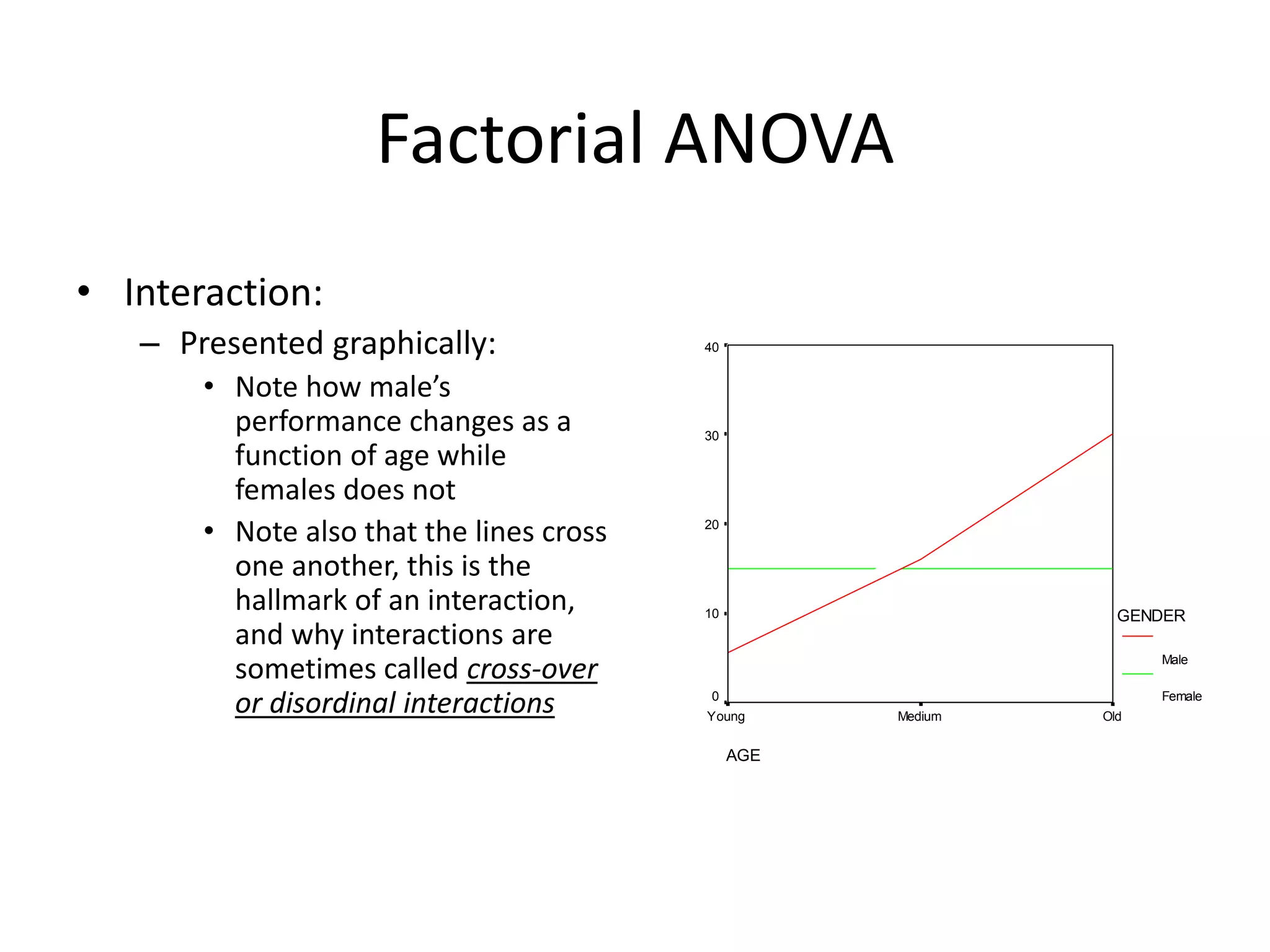
A two-way ANOVA analyzes the influence of two independent variables on a single dependent variable. It tests for main effects of each independent variable as well as interactions between the variables. The independent variables are categorical and the dependent variable is measured on an ordinal or ratio scale. It compares sums of squares and mean squares to determine if the means of observations grouped by each factor differ significantly. An example tests the effect of gender and age on test scores, with gender, age as independent variables and test score as the dependent variable.

1. BI FACTORIAL ANOVA (2- WAY
ANOVA)

2. Factorial ANOVA
• One-Way ANOVA = ANOVA with one IV with 1+
levels and one DV
• Factorial ANOVA = ANOVA with 2+ IV’s and one
DV
– Factorial ANOVA Notation:
• 2 x 3 x 4 ANOVA
• The number of numbers = the number of IV’s
• The numbers themselves = the number of levels in each
IV

3. Factorial ANOVA
• 2 x 3 x 4 ANOVA = an ANOVA with 3 IV’s, one of which has 2
levels, one of which has 3 levels, and the last of which has 4
levels
• Why use a factorial ANOVA? Why not just use
multiple one-way ANOVA’s?
1. Increased power – with the same sample size and effect
size, a factorial ANOVA is more likely to result in the
rejection of Ho
– aka with equal effect size and probability of rejecting Ho if it is
true (α), you can use fewer subjects (and time and money)

4. Factorial ANOVA
• Why use a factorial ANOVA? Why not just use
multiple one-way ANOVA’s?
2. With 3 IV’s, you’d need to run 3 one-way
ANOVA’s, which would inflate your α-level
– However, this could be corrected with a Bonferroni
Correction
3. The best reason is that a factorial ANOVA can
detect interactions, something that multiple
one-way ANOVA’s cannot do

5. Factorial ANOVA
• Interaction:
– when the effects of one independent variable differ
according to levels of another independent variable
– Ex. We are testing two IV’s, Gender (male and female) and
Age (young, medium, and old) and their effect on
performance
• If males performance differed as a function of age, i.e. males
performed better or worse with age, but females performance was
the same across ages, we would say that Age and Gender interact,
or that we have an Age x Gender interaction

6. Factorial ANOVA
• Interaction:
– Presented graphically:
• Note how male’s
performance changes as a
function of age while
females does not
• Note also that the lines cross
one another, this is the
hallmark of an interaction,
and why interactions are
sometimes called cross-over
or disordinal interactions
AGE
OldMediumYoung
Performance
40
30
20
10
0
GENDER
Male
Female

7. Factorial ANOVA
• Interactions:
– However, it is not necessary that the lines cross,
only that the slopes differ from one another
• I.e. one line can be flat, and the other sloping upward,
but not cross – this is still an interaction
• See Fig. 17.2 on page 410 in the text for more examples

8. Factorial ANOVA
• As opposed to interactions, we have what are
called main effects:
– the effect of an IV independent of any other IV’s
• This is what we were looking at with one-way ANOVA’s
– if we have a significant main effect of our IV, then we
can say that the mean of at least one of the
groups/levels of that IV is different than at least one of
the other groups/levels

9. Factorial ANOVA
• Finally, we also have simple effects:
– the effect of one group/level of our IV at one
group/level of another IV
• Using our example earlier of the effects of Gender
(Men/Women) and Age (Young/Medium/Old) on
Performance, to say that young women outperformed
other groups would be to talk about a simple effect

10. Factorial ANOVA
• We then calculate the Grand Mean ( )
– This remains (ΣX)/N, or all of our observations
added together, divided by the number of
observations
• We can also calculate SStotal, which is also
calculated the same as in a one-way ANOVA
..X
 
N
X
X
2
2 


11. Factorial ANOVA
• Next we want to calculate our SS terms for our
IV’s, something new to factorial ANOVA
– SSIV = nxΣ( - )2
• n = number of subjects per group/level of our IV
• x = number of groups/levels in the other IVIVX ..X

12. Factorial ANOVA
– SSIV = nxΣ( - )2
1. Subtract the grand mean from each of our levels means
• For SSgender, this would involve subtracting the mean for males from
the grand mean, and the mean for females from the grand mean
• Note: The number of values should equal the number of levels of
your IV
2. Square all of these values
3. Add all of these values up
4. Multiply this number by the number of subjects in each cell x
the number of levels of the other IV
5. Repeat for any IV’s
• Using the previous example, we would have both SSgender and SSage
IVX ..X

13. Factorial ANOVA
• Next we want to calculate SScells, which has a
formula similar to SSIV
– SScells =
1. Subtract the grand mean from each of our cell means
• Note: The number of values should equal the number of cells
2. Square all of these values
3. Add all of these values up
4. Multiply this number by the number of subjects in each cell
 2
..XXn cell 

14. Factorial ANOVA
• Now that we have SStotal, the SS’s for our IV’s,
and SScells, we can find SSerror and the SS for our
interaction term, SSint
– SSint = SScells – SSIV1 – SSIV2 – etc…
• Going back to our previous example,
SSint = SScells – SSgender – SSage
– SSerror = SStotal – SScells

15. Two Way ANOVA

16. Data required
• When 2 independent variables
(Nominal/categorical) have
an effect on one dependent variable
(ordinal or ratio measurement scale)
• Compares relative influences on Dependent Variable
• Examine interactions between independent variables
• Just as we had Sums of Squares and Mean Squares in
One-way ANOVA, we have the same in Two-way
ANOVA.

17. Two way ANOVA
Include tests of three null hypotheses:
1) Means of observations grouped by one factor
are same;
2) Means of observations grouped by the other
factor are the same; and
3) There is no interaction between the two factors.
The interaction test tells whether the effects of
one factor depend on the other factor

18. Example-
we have test score of boys & girls in age group of
10 yr,11yr & 12 yr. If we want to study the effect of
gender & age on score.
Two independent factors- Gender, Age
Dependent factor - Test score

19. Ho -Gender will have no significant effect on student
score
Ha -
Ho - Age will have no significant effect on student score
Ha -
Ho – Gender & age interaction will have no significant
effect on student score
Ha -

20. Two-way ANOVA Table
Source of
Variation
Degrees of
Freedom
Sum of
Squares
Mean
Square F-ratio
P-value
Factor A r  1 SSA MSA FA = MSA / MSE Tail area
Factor B c 1 SSB MSB FB = MSB / MSE Tail area
Interaction (r – 1) (c – 1) SSAB MSAB FAB = MSAB / MSE Tail area
Error
(within)
rc(n – 1) SSE MSE
Total rcn  1 SST

21. Example with SPSS
Example:
Do people with private health insurance visit their
Physicians more frequently than people with no
insurance or other types of insurance ?
N=86
• Type of insurance - 1.No insurance
2.Private insurance
3. TRICARE
• No. of visits to their Physicians(dependent
variable)
Gender
0-M
1-F

22. References
• Methods in Biostatistics by BK Mahajan
• Statistical Methods by SP Gupta
• Basic & Clinical Biostatistics by Dawson and
Beth
• Munro’s statistical methods for health care
research